EM算法和GMM模型

本章主要从概率论方面讲述了GMM模型和EM算法的底层原理，即通过已知推测未知，再通过上次所得到的结果，来推导下一轮的结果，直到这个结果与上一轮的结果误差在我们设定的范围内，就视为我们得到了想要的结果。

---

先验概率和后验概率

一个不确定的事件有一定的发生概率，这是出现了新事件，导致这个概率发生了变化。
那么，原来的那个概率叫先验概率，后面改变的这个概率叫后验概率。
举个例子：
古彩戏法三仙归洞，有三个倒扣的碗ABC，我们知道里面有个碗下面扣着一个球，这时候，球在ABC任何一个碗下面的概率都是1/3，这个叫做先验概率。当我们掀开A碗，发现下面没有球，那么球在B或者C碗里的概率变为1/2，这个叫后验概率。
资料来源：Deep Learning ｜ 先验概率和后验概率的区别 - 知乎

---

K-means聚类

是一个常见的聚类算法，简单来说，物以类聚人以群分。只不过我们的聚类标准就是需要被分类的点到各个聚类中心的欧式距离，到谁的距离最小，就属于哪个类别。

那么我们需要做的是两点：
第一，明确需要分多少类簇（即k的取值）；
第二，使所有点到其所属的聚类中心的欧氏距离之和最小。

那么可能会分3类情况：
第一种：知道K的值，知道聚类中心的值。一遍计算即可分类。
第二种：知道K的值，不知道聚类中心在哪里，此时通过迭代求取聚类中心，不断更新聚类中心的位置，从而获得结果
第三种：不知道K的值，此时需要通过肘部法来判断K的值，之后在通过第二种方式再进行聚类。

肘部法则：

如果问题中没有指定k的值，可以通过肘部法则这一技术来估计聚类数量。肘部法则会把不同k值的成本函数值画出来。随着k值的增大，平均畸变程度会减小；每个类包含的样本数会减少，于是样本离其重心会更近。但是，随着k值继续增大，平均畸变程度的改善效果会不断减低。k值增大过程中，畸变程度的改善效果下降幅度最大的位置对应的k值就是肘部。为了让读者看的更加明白，下面让我们通过一张图用肘部法则来确定最佳的k值。下图数据明显可分成两类：

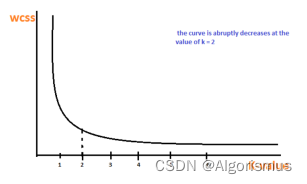
轮廓系数

除了欧氏距离，轮廓稀系数首先是用来评价一个样本的归属划分效果的。假设点i归属于m号簇，而距离点i最近的其他簇是n号簇计算方式为：

之后把所有样本点的系数相加，得到整体的轮廓系数，一般选用最高的值作为结果。

资料来源：Kmeans聚类算法简介（有点枯燥） - 简书
kmeans聚类算法及其python实现 - 知乎

计算聚类的步骤：

1.选点：随机选取K个点，作为质心（最好选择相距远一点的点）
2.分类：对其余点进行分类，标准是欧氏距离
3.更新质心：对每个类中的点计算他们的平均值，作为这个类别中新的聚类中心。
4.与上次的聚类中心进行比对，看是否有变化。如果无，则代表已经完成聚类，如果有，则返回第2步继续分类。

代码实现可以参考：
不足20行 python 代码，高效实现 k-means 均值聚类算法_天元浪子的博客-CSDN博客 https://blog.csdn.net/xufive/article/details/101448969

---

EM算法

EM 算法是 Dempster,Laind,Rubin 于 1977 年提出的求参数极大似然估计的一种方法，它可以从非完整数据集中对参数进行 MLE 估计，是一种非常简单实用的学习算法。这种方法可以广泛地应用于处理缺损数据，截尾数据，带有噪声等所谓的不完全数据。
可以有一些比较形象的比喻说法把这个算法讲清楚。比如说食堂的大师傅炒了一份菜，要等分成两份给两个人吃，显然没有必要拿来天平一点的精确的去称分量，最简单的办法是先随意的把菜分到两个碗中，然后观察是否一样多，把比较多的那一份取出一点放到另一个碗中，这个过程一直迭代地执行下去，直到大家看不出两个碗所容纳的菜有什么分量上的不同为止。
EM算法就是这样，假设我们估计知道A和B两个参数，在开始状态下二者都是未知的，并且知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止。

原理：

假定集合z=(x,y)由观测数据x和未观测数据y组成，x和z=(x,y)分别称为不完整数据和完整数据。假设Z的联合概率密度被参数化地定义为p(x,y|θ)，其中θ表示要被估计的参数。θ的最大似然估计是求不完整数据的对数似然函数L(x;θ)的最大值而得到的：

接下来便是E步：(作者不太熟悉LaTeX，先上手写笔记，之后补上)
计算 $\log p(x,z|\theta )$ 在概率分布 $p(z|x,{\theta }^t)$ 下的期望

接下来是M步：
计算使这个期望最大化的参数得到下一个 EM 步骤的输入

---

GMM模型

定义：
GMM，高斯混合模型，也可以简写为MOG。高斯模型就是用高斯概率密度函数（正态分布曲线）精确地量化事物，将一个事物分解为若干的基于高斯概率密度函数（正态分布曲线）形成的模型

所以需要了解高斯分布（高中知识）：

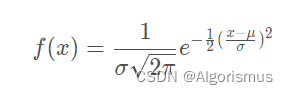
推广一下，D维高斯分布：

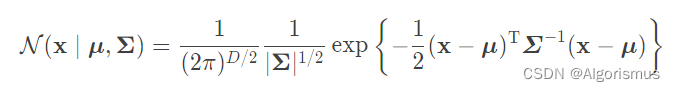
其中：μ∈R^D，是高斯分布的均值向量
Σ属于R^(D*D)，是高斯分布的协方差矩阵
D表示维度，也是向量总数

参考资料：协方差的意义和计算公式 - ywl925 - 博客园
多元高斯概率分布函数的推导与理解 - 知乎

最大似然估计

就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。
大学期间概率论告诉我们连续变量的最大似然计算是：

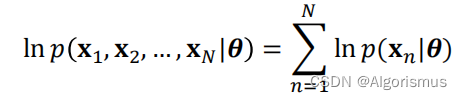
变形为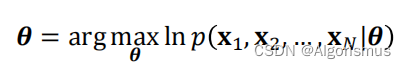

（注：arg max f(x): 当f(x)取最大值时，取x的取值）

推广到高斯模型：

现在回到GMM模型来，它把这些复杂的波形图视为多个高斯分布的组合体，只不过这个组合里每个高斯分布的权重不同。因此我们得到高斯混合分部的公式：

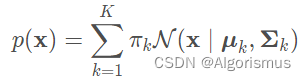
其中：0≤πk≤1
πk是权重，加起来为1
我们需要求解的就是πk，μk和Σk

注意：这里的π不是3.14那个圆周率，它是一个代数字母，可以使α可以使β等等。

这时候需要引入一个概念πk：
一个K维的one-hot，向量z=[z1,z2,…,zk],zk∈{0,1}，Σkzk=1.
P(zk=1)为向量z的第k维为1的先验概率，即：P(zk=1)=πk；
向量z的分部可以表示为：

那么现在回到GMM模型的条件分布：

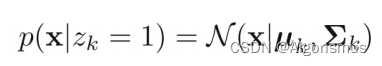
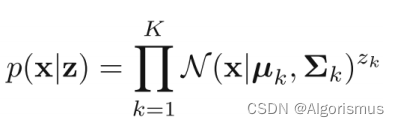
联合分布则是：

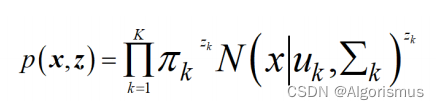
那么可以推导出边缘分布为：

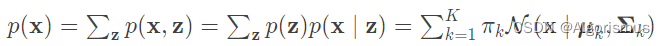
这里可以推导出潜变量p(x)，这时可以更新γ(zk)

推导过程：

资料参考：
【机器学习】【白板推导系列】【合集 1～33】_哔哩哔哩_bilibili

作业地址
鉴于只需要增加俩函数，所以只上传了这个文件，如想看完整作业可去老师布置作业的地址
P.S.我跑出来的结果是：acc=0.9727272727272728