文章目录

模型名称描述
平滑法削弱短期随机波动对序列的影响，序列插值分布均匀
趋势拟合法把时间作为自变量，相应序列观察值作为因变量，简历回归模型
组合模型法受长期趋势（T）、季节变动（S）、周期变动（C）和不规则变动（ε）四个因素影响
组合模型（1）加法模型： T + S + C + ϵ T+S+C+\epsilon T+S+C+ϵ （2）乘法模型： T S C ϵ T SC\epsilon TSCϵ

常见时间序列模型

模型名称描述
AR模型考虑历史数据的影响，以过往数据为自变量， X t X_t Xt​为因变量建立线性回归模型。 X t = ϕ 0 + ϕ 1 x t − 1 + ⋯ + ϕ p x t − p X_t=\phi_0+\phi_1 x_{t-1}+\cdots+\phi_p x_{t-p} Xt​=ϕ0​+ϕ1​xt−1​+⋯+ϕp​xt−p​
MA模型忽略历史数据影响，建立于前q期随机扰动 ϵ t − 1 , ⋯   , ϵ t − q \epsilon_{t-1},\cdots,\epsilon_{t-q} ϵt−1​,⋯,ϵt−q​的线性回归模型 X t = μ + ϵ t − θ 1 ϵ t − 1 − ⋯ − θ q ϵ t − q X_t=\mu+\epsilon_t-\theta_1 \epsilon_{t-1}-\cdots-\theta_q \epsilon_{t-q} Xt​=μ+ϵt​−θ1​ϵt−1​−⋯−θq​ϵt−q​
ARMA模型结合考虑AR、MA模型，综合考虑它们的影响
ARIMA模型针对非平稳序列。将非平稳转化为平稳后拟合操作

1. 基本概念

白噪声序列： 数据随机分布，没有规律。
平稳非白噪声序列
非平稳序列： 可以利用差分法转换为平稳非白噪声序列
截尾： 拖尾指序列以指数率单调递减或震荡衰减
拖尾： 截尾指序列从某个时点变得非常小
在这里插入图片描述

1.1 自相关函数ACF（autocorrelation function）

  • 自相关函数反映了同一序列在不同时序的取值之间的相关性。
  • 公式：
    A C F ( k ) = ρ k = C o v ( y t , y t − k ) V a r ( y t ) ACF(k) = \rho_k=\frac{Cov(y_t,y_{t-k})}{Var(y_t)} ACF(k)=ρk​=Var(yt​)Cov(yt​,yt−k​)​
    其中， ρ k ∈ [ − 1 , 1 ] \rho_k \in[-1,1] ρk​∈[−1,1]

1.2 偏自相关函数PACF（partial autocorrelation function）

  • 剔除了中间k-1个随机变量 x ( t − 1 ) , x ( t − 2 ) , ⋯   , x ( t − k + 1 ) x(t-1),x(t-2),\cdots,x(t-k+1) x(t−1),x(t−2),⋯,x(t−k+1)的干扰后 x ( t − k ) x(t-k) x(t−k)对 x ( t ) x(t) x(t)影响的相关程度
  • PACF是严格两个变量之间的相关性。

2. 常见模型

2.1 自回归模型（AR）

定义：

  • 描述当前值与历史值之间的关系。利用历史数据对自身进行预测

  • P阶自回归过程，即当前值与 t − p , t − p + 1 , ⋯   , t − 1 t-p,t-p+1,\cdots,t-1 t−p,t−p+1,⋯,t−1相关（P）。
    y t = μ + ∑ i = 1 p γ i y t − i + ϵ t y_t=\mu+\sum_{i=1}^{p} \gamma_i y_{t-i} + \epsilon_t yt​=μ+i=1∑p​γi​yt−i​+ϵt​
    其中， y t y_t yt​是当前值， μ \mu μ是常数项，P是阶数， γ i \gamma_i γi​是自相关系数， ϵ \epsilon ϵ是误差。

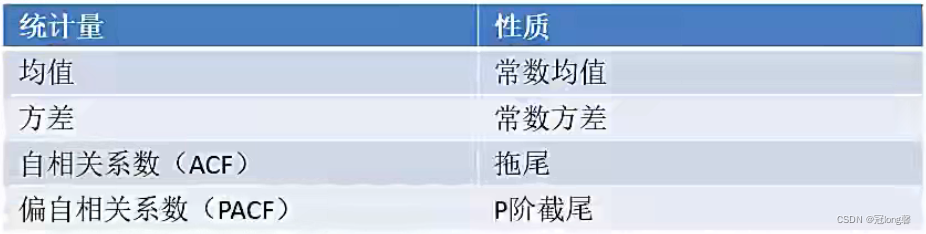
  • 参数：P（自回归阶数）

注意

  • 必须具有平稳性
  • 必须具有自相关性，自相关系数需要大于等于0.5.

模型识别
在这里插入图片描述

2.2 移动平均模型（MA）

定义

  • 移动平均模型是自回归模型中误差项的累加

  • q阶移动模型公式（Q）：
    y t = μ + ϵ t + ∑ i = 1 q θ i ϵ t − i y_t = \mu + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t-i} yt​=μ+ϵt​+i=1∑q​θi​ϵt−i​

  • 移动平均法能有效地消除预测中的随机波动

  • 参数：Q（移动平均阶数）

模型识别
在这里插入图片描述

2.3 自回归移动平均模型（ARMA）

定义

  • 自回归与移动平均的结合

  • 公式定义为（P,Q）：
    y t = μ + ∑ i = 1 p γ i y t − i + ϵ t + ∑ i = 1 q θ i ϵ t − i y_t = \mu + \sum_{i=1}^{p} \gamma_i y_{t-i} + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t-i} yt​=μ+i=1∑p​γi​yt−i​+ϵt​+i=1∑q​θi​ϵt−i​

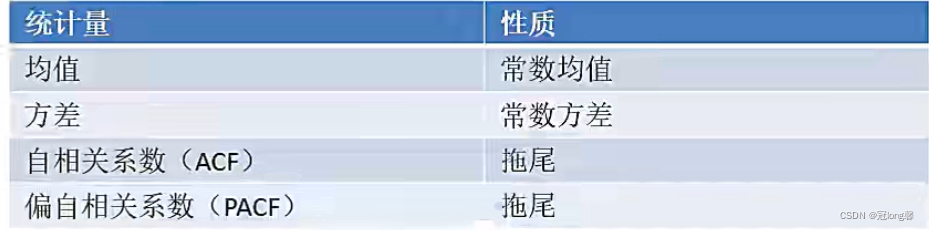
  • 参数：P（自回归阶数），Q（移动平均阶数）

模型识别
在这里插入图片描述

2.4 差分自回归移动平均模型（ARIMA）

对于ARIMA模型，我们需要指定三个参数（P, D, Q），分别表示P阶自回归模型，D阶差分和Q阶移动平均模型。
定义：

  • 参数：（P, D, Q），分别表示P阶自回归模型，D阶差分和Q阶移动平均模型。
  • 原理：将非平稳时间序列转换为平稳时间序列，然后将因变量对其滞后值和其随机误差的滞后值进行回归建模。

4. 建模步骤

4.1 平稳性检验

4.1.1 时序图、自相关图、偏自相关图

def tsplot(y,lags=None,figsize=(12,7),style='bmh'):
    '''
    Plot time series, its ACF and PACF, calculate Dickey-Fuller test
    y:timeseries
    lags:how many lags to include in ACF,PACF calculation
    '''
#     if not isinstance(y, pd.Series):
#         y = pd.Series(y)
    with plt.style.context(style):
        fig = plt.figure(figsize=figsize)
        layout=(2,2)
        ts_ax = plt.subplot2grid(layout, (0,0), colspan=2)
        acf_ax = plt.subplot2grid(layout, (1,0))
        pacf_ax = plt.subplot2grid(layout, (1,1))

        y.plot(ax=ts_ax)
        p_value = sm.tsa.stattools.adfuller(y)[1]
        ts_ax.set_title('Time Series Analysis Plots\n Dickey-Fuller: p={0:.5f}'.format(p_value))
        smt.graphics.plot_acf(y,lags=lags, ax=acf_ax)
        smt.graphics.plot_pacf(y,lags=lags, ax=pacf_ax)
        plt.tight_layout()    
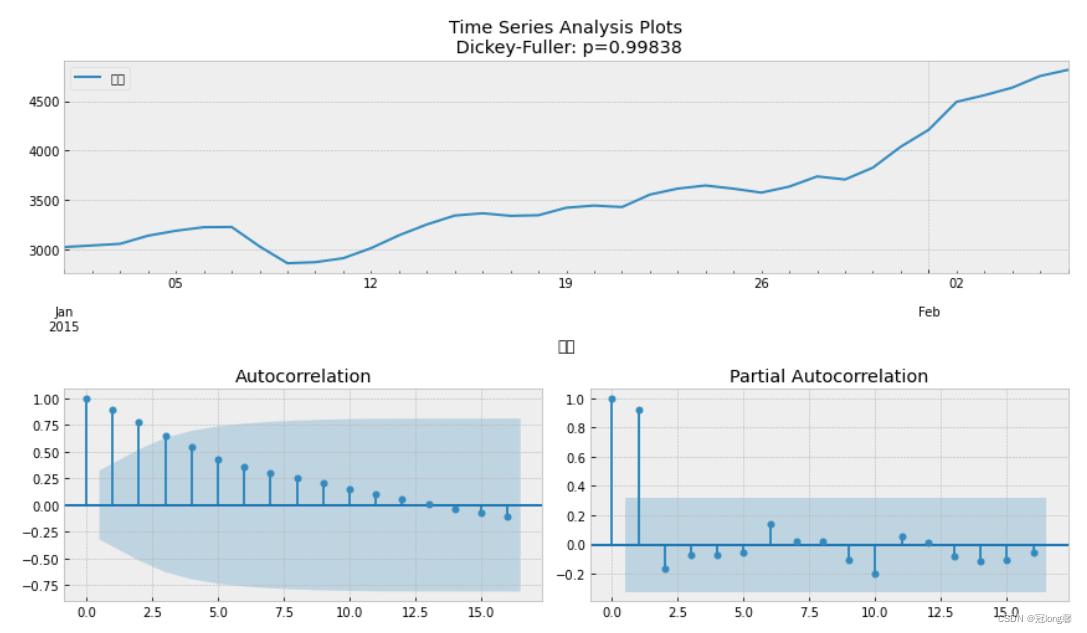
tsplot(data)

在这里插入图片描述

4.1.2 自相关、偏自相关图

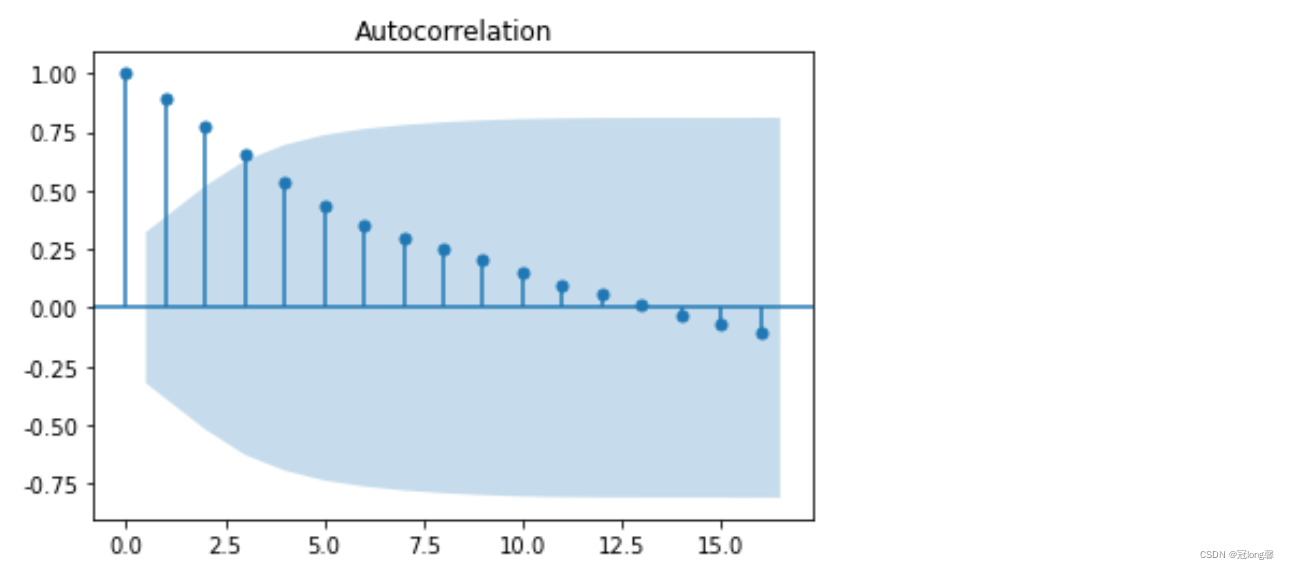
根据自相关图，判断“拖尾”、“截尾”。

from statsmodels.graphics.tsaplots import plot_acf
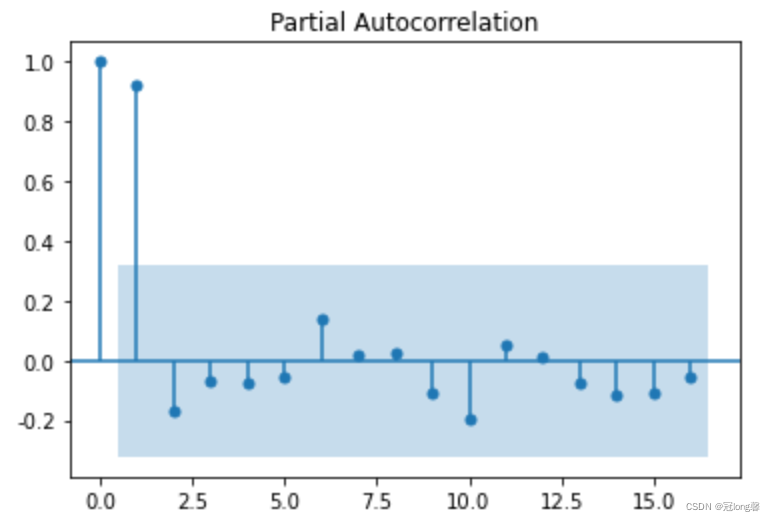
plot_acf(data).show()

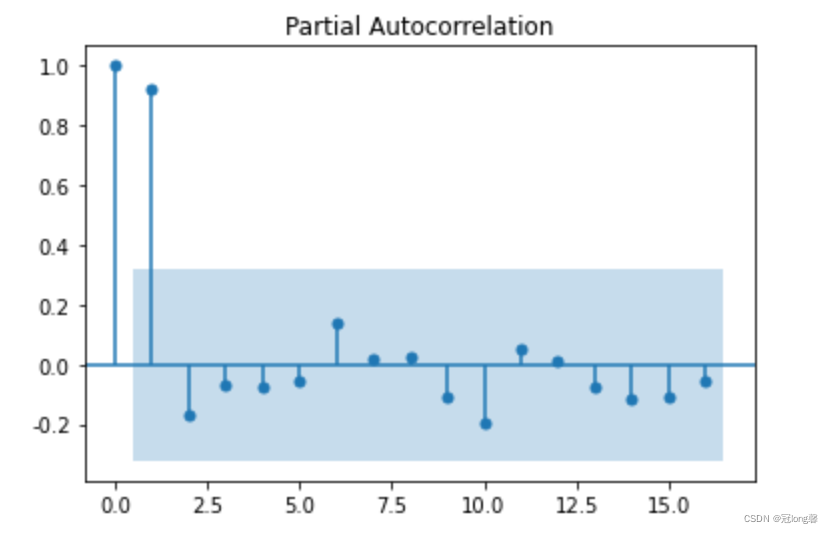
在这里插入图片描述

from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(data).show()

在这里插入图片描述

4.1.3 单位根检验

采用单位根法检验，当单位根大于等于0.05时，表示数据为非平稳序列。

from statsmodels.tsa.stattools import adfuller as ADF
print('原始序列数据的ADF检测结果为：')
print(ADF(data['销量']))
# 返回值依次为： adf, pvalue(单位根，>=0.05就是非平稳序列)

原始序列数据的ADF检测结果为：
(1.813771015094526, 0.9983759421514264, 10, 26, {‘1%’: -3.7112123008648155, ‘5%’: -2.981246804733728, ‘10%’: -2.6300945562130176}, 299.4698986602418)

4.1.4 差分运算

若序列为非平稳序列，则需要转换为平稳序列计算
（1）差分运算

  • P阶差分
    相距一期的两个序列之间的减法运算称为1阶差分运算
    将1阶差分运算的结果再做一次差分运算则称为2阶差分运算
  • K步差分
    相距k期的两个序列值之间的减法运算称为k步差分运算

1. 差分运算

D_data = data.diff().dropna()    # 一阶一步差分,并去除NA
D_data.columns = ['sale diff']

2. 差分结果检验
对差分结果进行相同的平稳性检验，当单位根值小于等于0.05时，表示已经转换为平稳序列。

# 自相关图
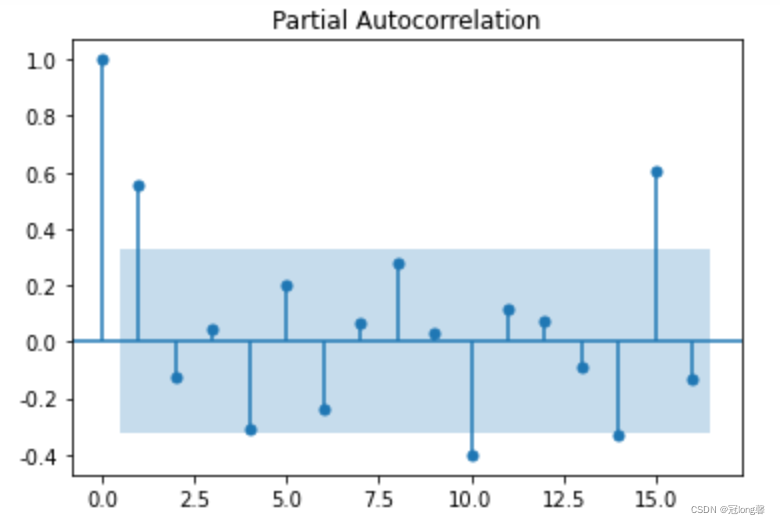
plot_acf(D_data).show()
# 偏自相关图
plot_pacf(D_data).show()
# 单位根值
print('原始序列数据进行一次一步差分的ADF检测结果为：')
print(ADF(D_data['sale diff']))

在这里插入图片描述
在这里插入图片描述
原始序列数据进行一次一步差分的ADF检测结果为：
(-3.1560562366723537, 0.022673435440048798, 0, 35, {‘1%’: -3.6327426647230316, ‘5%’: -2.9485102040816327, ‘10%’: -2.6130173469387756}, 287.5909090780334)

4.2 白噪声检验

from statsmodels.stats.diagnostic import acorr_ljungbox
print('差分序列的白噪声检验结果：')
print(acorr_ljungbox(D_data,lags=1))   # 返回统计量与p值，当p <= 0.05 时，不是白噪音

差分序列的白噪声检验结果：
(array([11.30402222]), array([0.00077339]))

4.3 模型选择（p,q,d）

AR, MA模型
通过ACF, PACF截尾开始阶数确定p, q参数值。

  • AR§：PACF上截尾，ACF趋近于0
  • MA(Q)：ACF上截尾，PACF趋近于0

采用BIC矩阵，找到最小值对应的p, q值。并以此为参数选择下述三个模型：
在这里插入图片描述

4.3.1 AIC与BIC

AIC：赤池信息准则（Akaike information Criterion）
A I C = 2 k − 2 ln ⁡ ( L ) AIC = 2k-2\ln(L) AIC=2k−2ln(L)

BIC：贝叶斯信息准则（Bayesian information Criterion）
B I C = k ln ⁡ ( n ) − 2 ln ⁡ ( L ) BIC = k\ln(n)-2\ln(L) BIC=kln(n)−2ln(L)

其中，k为模型参数个数，n为样本数量，L为似然函数。

  • AIC, BIC值越低越好
  • 希望通过AIC, BIC选择更简单的模型，P, Q越大，所需参数项数目越多。
from statsmodels.tsa.arima_model import ARIMA
# 定阶
# data['销量']=data['销量'].astype(float)
pmax = int(len(D_data)/10)
qmax = int(len(D_data)/10)

bic_matrix = []          # BIC矩阵
for p in range(pmax+1):
    tmp = []
    for q in range(qmax+1):
        try:    # 部分报错，跳过
            tmp.append(ARIMA(data,(p,1,q)).fit().bic)
        except:
            tmp.append(None)
    bic_matrix.append(tmp)

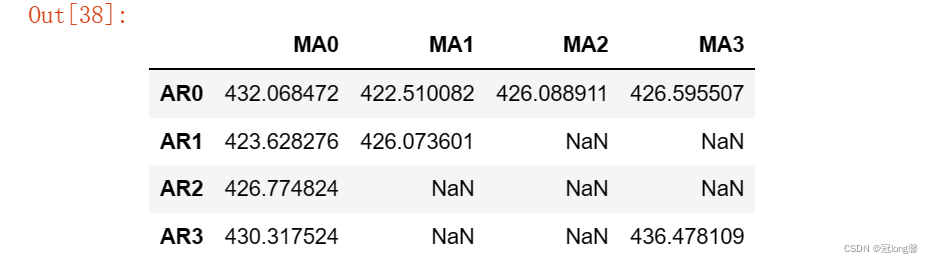
bic_matrix = pd.DataFrame(bic_matrix)
bic_matrix.index = ['AR{}'.format(i) for i in range(pmax+1)]
bic_matrix.columns = ['MA{}'.format(i) for i in range(qmax+1)]
bic_matrix = bic_matrix[bic_matrix.columns].astype(float)

p,q = bic_matrix.stack().idxmin()
print('最小BIC对应的p,q值：%s, %s'%(p,q))

在这里插入图片描述
最小BIC对应的p,q值：0, 1

import seaborn as sns
fig, ax = plt.subplots(figsize = (10,8))
ax = sns.heatmap(bic_matrix,
                mask = bic_matrix.isnull(),
                ax = ax,
                annot = True,
                fmt='.2f')
ax.set_title('BIC')

在这里插入图片描述

result = smt.arma_order_select_ic(data, ic=['aic', 'bic'], trend='nc', max_ar=4, max_ma=4)

{‘aic’: 0 1 2 3 4
0 NaN 668.212060 627.212365 590.498371 565.724666
1 472.121781 442.706792 444.414985 441.613728 442.640421
2 449.878586 443.006993 445.873538 443.364868 445.454087
3 452.992514 441.894814 443.613869 449.670033 442.185777
4 454.442210 443.477934 445.326246 445.745273 445.296295,
‘bic’: 0 1 2 3 4
0 NaN 671.433896 632.045119 596.942043 573.779256
1 475.343616 447.539546 450.858657 449.668317 452.305928
2 454.711339 449.450664 453.928128 453.030375 456.730513
3 459.436186 449.949403 453.279376 460.946459 455.073120
4 462.496800 453.143442 456.602672 458.632617 459.794557,
‘aic_min_order’: (1, 3),
‘bic_min_order’: (1, 1)}

由此可以选择MA模型，或者p =0, q =1的ARMA模型。可以将做完差分的数据带入平稳模型或者将原数据带入非平稳模型，并设置阶数。

4.3.2 模型稳定性检验

模型残差检验

  • ARIMA的残差是否是平均值为0且方差为常数的正太分布
  • QQ图：线性即正太分布

4.4 模型预测

model = ARIMA(data, (p,1,q)).fit()
print('模型报告为：\n', model.summary2())
print('未来5天的预测结果、准确误差及置信区间：\n',model.forecast(5))

# 机器学习 # 人工智能 # 深度学习
Logo
CSDN学习社区

CSDN联合极客时间，共同打造面向开发者的精品内容学习社区，助力成长！

更多推荐

cover

用 OpenAI Assistants 做大模型应用开发

avatar CSDN学习社区
cover

1 小时解读鸿蒙 10 大热点问题

avatar CSDN学习社区
cover

1 小时解读鸿蒙 10 大热点问题

avatar CSDN学习社区