论文

ID3 算法论文：《Induction of decision trees》
C4.5: 算法书籍： 《Programs for Machine Learning》
CART 算法书籍：《Classification and regression trees》、《Pattern Recognition and Neural Networks》

介绍

电信保温杯笔记——《统计学习方法（第二版）——李航》
本文是对原书的精读，会有大量原书的截图，同时对书上不详尽的地方进行细致解读与改写。

决策树(decision tree）是一种基本的分类与回归方法。本章主要讨论用于分类的决策树．在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。决策树学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪。

特点

模型具有可读性，分类速度快.，可用于分类与回归。

信息论基础

熵

当一件事总是发生，或者总是不发生，我们认为这是没有信息的；而一件事发生的概率很小，不确定性越高，比如太阳从西边升起，那么我们认为这是蕴含了大量信息的，那么我们怎么衡量这些信息的多少呢？于是我们定义 $\log \frac{1}{p}=-\log p$ 为这件事的惊讶程度，再乘上它发生的概率 $-p\log p$ 就是它的期望，也就是这件事发生所蕴含的信息量。由于它的表达式与热力学中的熵的表达式相似，于是就把它叫做熵。

根据洛必达法则：
$$\underset{p\to 0}{\lim }p\log p=\underset{p\to 0}{\lim }\frac{\log p}{\frac{1}{p}}=\underset{p\to 0}{\lim }\frac{\frac{1}{p}}{-\frac{1}{p^2}}=\underset{p\to 0}{\lim }p=0$$

概率与熵的关系

当 $X$ 的取值不为2值时，而是有M个取值时，事件 $X$ 的每个取值的概率如何分布，它的熵 $H(X)$ 才是最大的呢？答案是 $p_i=\frac{1}{M},i=1,2,...,M$。下面从定性和定量两个角度分析。

定性分析

当 $p_i=\frac{1}{M}$ 时，$X$ 的取值不确定性是最高的，因为它们每个的概率都是相等的，这时你最无法判断是M个取值中的哪一种情况。如果概率不是均等的，而是有一个比其他的取值要大一点，这个时候不确定性就降低了，因为那个取值的概率大一点，这时它的熵 $H(X)$就会比概率均值的时候要小了。

定量分析

令
$$f(p)=-p\log p,p\in [0,1]$$
$$f^{\prime }(p)=-(\log p+p\cdot \frac{1}{p})=-(\log p+1)$$
导数和原函数图像为：

由此我们知道，当概率 $p_i$ 很大或很小时，它的熵是很小的，当它接近中间值1/2时最大，由此可知，$X$ 有M个取值时，$p_i=\frac{1}{M},i=1,2,...,M$ 时，它的熵$H(X)$ 最大，它含有的信息量是最多的。

条件熵

上式中的 $H(Y|X=x_i)$ 为 $X=x_i$ 的样本中，事件 $Y$ 的熵，是已知 $X=x_i$ 的情况下计算出来的：
$$H(Y|X=x_i)=\sum _{j=1}^m-p(Y=y_j|X=x_i)\log p(Y=y_j|X=x_i)$$

对条件熵的解释：

假设现在有一个盒子，盒子里面有一个球，只可能是白球或者红球，定义事件 $Y$ 为盒子里面有一个球，$Y=$ 白球或者红球，定义事件 $X$ 为盒子内壁的颜色，$X=$ 白色或者红色。

我们可以直接计算出事件 $Y$ 的熵，即盒子的信息量 $H(Y)$，但现在多了一个事件，一个条件 $X$，在知道了一个条件下，此时计算事件 $Y$ 的熵，就是条件熵，即知道了盒子内壁颜色的条件下，知道盒子内壁颜色这个信息之后，再计算盒子的信息量。那么这个时候计算出来的条件熵就可能不是原来的熵了，因为假如球是掉色的，那么条件 $X$ 其实是对推断事件 $Y$ 的结果是有影响的。信息量就是熵，信息量增加，熵就增加，信息量减少，熵就减少。我们得知了内壁颜色这个信息之后，事件 $Y$ 的信息量是应该减少的，此时计算的条件熵 $H(Y|X)$ 就应该比原来的熵 $H(Y)$ 要小。假如球是不掉色的，那么内壁颜色这个条件其实是对对推断事件 $Y$ 的结果是没有影响的，此时计算的条件熵 $H(Y|X)$ 等同于原来的熵 $H(Y)$。

信息增益

信息增益 = 事件 $Y$ 的信息量 $H(Y)$ $-$（得知事件 $X$ 后）事件 $Y$ 的信息量 $H(Y|X)$

信息增益又称为互信息，换句话说，就是事件 $Y$ 与事件 $X$ 中互通的部分，2件事共享的信息量。因此，如果信息增益比较大，则证明
事件 $X$ 可以很好地帮我们推断事件 $Y$，即盒子内壁颜色这个事件可以很好地帮我们推断盒子中球的颜色。由此可见，信息增益可以帮助我们进行样本的分类。

信息增益比

更多关于熵的概念

熵与信息增益
损失函数之交叉熵(一般用于分类问题)

决策树的原理

步骤

例子

信息增益比的引入

树的生成算法

ID3 算法

步骤

例子

C4.5 算法

步骤

树的剪枝算法

原理

叶节点上的点并非全部都是同一类的，所以叶节点的经验熵不为零，如果全部都是一类，经验熵就是零，所以此时经验熵等同于预测误差，而且是节点上样本的平均预测误差，所以公式（5.11）在计算时还要乘上该节点上的样本数。

公式（5.14）中，$C(T)$ 越小，代表叶节点上的样本越纯（同一类），过拟合程度就越高，所以加入 $\alpha |T|$ 其实是一个惩罚项，起到正则化的作用。

步骤

树的生成加剪枝算法

CART 算法

CART 的生成

回归树的生成

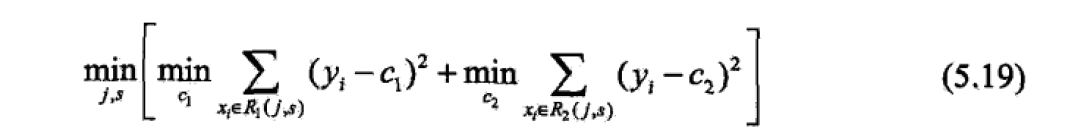
步骤

分类树的生成

基尼指数

基尼指数与概率的关系

命题：基尼指数越大，样本的不确定性就越高，不确定性最高为 $p_i=\frac{1}{K},i=1,2,...,K$ 的时候

证明：
基尼指数越大，$\sum _{k=1}^K{p}_k^2$ 就越小，那我们就先探究 $p_1^2+p_2^2$ 与概率 $p_1,p_2$ 的关系
令
$$p_1+p_2=m,p_1\in [0,m],m\in [0,1-p_1-p_2]$$
则
$$p_1^2+p_2^2=2(p_1-\frac{m}{2}{)}^2+{\frac{m}{2}}^2$$
可知，$p_1=p_2$ 时，$p_1^2+p_2^2$ 最小；再随机挑选2个概率 $p_i,p_j$，可知他们相等时 $p_i^2+p_j^2$ 最小，基尼指数越大；直至 $p_i=\frac{1}{K},i=1,2,...,K$ 时，基尼指数越大，这时样本的不确定性也是最高的。

这样看，基尼指数与熵的含义其实是类似的。

结论：基尼指数越小，样本的确定性就越高，样本类别越集中。


基尼指数 Gini$(D,A)$ 越小，表示经过特征A分类之后，样本的确定性提高，样本变得越集中越纯净，分类效果就越好。

步骤

例子

CART 的剪枝

形成子树序列

交叉验证择出最优子树

步骤

交验验证

交叉验证与训练集、验证集、测试集
训练集、验证集、测试集以及交验验证的理解

本章概要

相关视频

相关的笔记

hktxt /Learn-Statistical-Learning-Method
熵与信息增益
损失函数之交叉熵(一般用于分类问题)
交叉验证与训练集、验证集、测试集
训练集、验证集、测试集以及交验验证的理解

相关代码

Dod-o /Statistical-Learning-Method_Code，写的是ID3算法。

pytorch

tensorflow

keras

pytorch API:

tensorflow API