光波传输的角谱理论【理论，实例及matlab代码】

fightandstrive

26590人浏览 · 2022-01-20 12:49:27

fightandstrive · 2022-01-20 12:49:27 发布

1.理论基础

光波在自由空间中的传播可以通过多种理论来描述。最常用的就是菲涅尔衍射传播、夫朗禾费衍射传播以及角谱理论。

本质上来说，三者是一致的，只是适用条件有所不同。弗朗禾费衍射因为近似条件较为苛刻一般来说是在自由空间的远场或者透镜系统中较为常见。菲涅尔衍射的近似条件较为简单，只需要在近轴区域，一般来说都适用，但是它的计算过程相比弗朗禾费而言更加复杂。基于衍射的传播理论是在空域对光波进行描述，而角谱理论对光波进行了抽象，从频域进行分析，任何的复杂光波都可以认为是由各种频率分量的平面光波组成，每一个平面光波都是一个面基元。例如复杂光波 $\displaystyle E(x,y)$ 可以分解为

$E(x,y)=\int e(f_x,f_y)\textup{exp}[j2\pi(f_xx+f_yy)]df_xdf_y$

观察上式可以发现，指数项实际是一个频率为 $\displaystyle f_x$ 和 $f_y$ 的平面光波， $e(f_x,f_y)$ 是其对应的权重，习惯上被称为频谱函数。回顾傅里叶变换基本理论，可以发现对频谱函数作逆傅里叶变换得到了光波函数，对光波作傅里叶变换就得到了频谱函数，在MATLAB里面，可以通过fft(一维)或者fft2（二维）实现快速转变。

利用角谱理论分析问题的一般流程如图1所示。假定在自由空间中有两个平面，z=0的输入面 $\tiny \displaystyle \sum$ 以及z=z的输出平面 $\displaystyle$ $\tiny \displaystyle \prod$ ，在输入面有一个任意的光波函数 $A(x,y)$ ，我们的目的就是确定其在自由空间传递到输出面时的光波函数 $E(x,y)$ 。首先，对 $A(x,y)$ 作傅里叶变换得到其频谱 $a(f_x,f_y)$ ，再乘上传递函数 $H(f_x,f_y)$ 得到输出面的频谱 $e(f_x,f_y)$ ，作逆傅里叶变换得到输出面的波函数 $E(x,y)$ 。所需要解决的关键问题就是确定传递函数 $H(f_x,f_y)$ 。

光波函数 $A(x,y)$ 的频率为 $\displaystyle f_x$ 和 $f_y$ 的成分为 $a(f_x,f_y)df_xdf_y\textup{exp}[2j\pi(f_xx+f_yy)]$ ，光波函数 $E(x,y)$ 的对应的成分为 $a(f_x,f_y)df_xdf_y\textup{exp}[2j\pi(f_xx+f_yy+f_zz)]$ ，比较两个函数，可以发现输出面相比于输入面多了一项 $exp(2j\pi f_zz)$ ，且

$f_z=\sqrt{(\frac{1} {\lambda})^2-f_x^2+f_y^2)}$

所以可以得到自由空间的传递函数

$H(f_x,f_y)=\textup{exp}(j2\pi z \sqrt{(\frac{1}{\lambda})^2-f_x^2-f_y^2)}$

2.实例演示

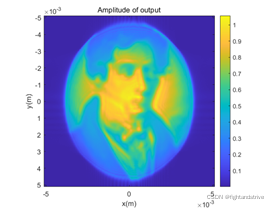
根据上面介绍的原理，可以实现一些非常有趣的衍射现象。假定采用一个振幅分布为归一化高斯型的光源（大小10.24mm*10.24mm，波长532nm，束腰为5.32mm，如图2所示）照射一个自由曲面（最大厚度为3mm，面型储存在z_g.mat矩阵中，如图3所示）。那么采用上面的分析，可以得到其在自由空间传播200mm后得到一张菲涅尔的图像，如图4所示，十分有趣。

3.MATLAB代码

clc;
clear all;
close all;
%% Generate the input Gaussian beam
mm=1e-3;
nm=1e-9;
lambda=532*nm;% wavelength
k=2*pi/lambda;% wavevector
n=1.494;% The rafractive index of freeform elements 
SL=10.24*mm ;% Side length
N=512*1;% samples for side length
dx=SL/N;%sample interval
d=200*mm;% The distance between the input and output planes
x = -0.5*SL:dx:0.5*SL-dx;% coordinate
y = x;
[X,Y]=meshgrid(x,y);
I_input=exp(-2*((X /(0.5* SL)).^2+(Y/(0.5* SL)).^2)); %The input Gaussian beam
figure;
imagesc(x,y,I_input);
axis square;
xlabel('x(m)');
ylabel('y(m)');
colorbar;
title('Amplitude of Gaussian beam');


%% phase modulataion by the freeform surface
load('z_g.mat');
OPD = 3*mm+(n-1)*z_g;
P_input  = exp(1i*k*OPD);
figure;mesh(X,Y,z_g);
title('Surface of lens');
xlabel('x(m)');
ylabel('y(m)');
zlabel('t(m)');
u1 = I_input.*P_input;

%% obtain the output field using Angular spectrum
fx=-1/(2*dx):1/SL:1/(2*dx)-1/SL;  %freq coords
[FX,FY]=meshgrid(fx,fx);
H=exp(1i*k*d*sqrt(1-(lambda*FX).^2-(lambda*FY).^2));  %trans func
H=fftshift(H);
U1=fft2(fftshift(u1));  %shift.fft source filed
U2=H.*U1;    %multiply
u2=fftshift(ifft2(U2));
figure;
imagesc(x,y,abs(u2));
axis square;
xlabel('x(m)');
ylabel('y(m)');
colorbar;
title('Amplitude of output');