Lecture1 计算机图形概述

一、图形学的内容

1、矩阵，曲线表面
2、物理、灯光、着色
3、操作几何形体
4、模拟、动画、解算

二、课程内容

1、光栅化
把三维空间的几何形体显示再屏幕上（实时30+fps）
2、曲线和曲面的操作
表示曲线和曲面
3、光线追踪
渲染真实的画面，牺牲速度、offline
4、模拟、动画、解算

三、图形学和计算机视觉

需要猜测的操作都可以认为是计算机视觉
二者目前越来越没有明显的界限
±------------

Lecture2 向量与线性代数

一、学习图形学所需的知识

1、基础数学线性代数
2、基础物理：光学、力学
3、其他：信号处理、数值处理

二、向量

空间中具有方向的量

1、向量可以写作
$$\vec{a}$$
2、对于向量AB，可以用B-A表示
3、向量同时具有方向和长度
4、向量没有绝对的开始位置，如图所示向量AB和向量A’B’表示的是同一个向量
5、向量的归一化
向量的长度单位写作||a||
单位向量：表示长度为1的向量
计算一个向量的单位向量被称为归一化，计算方法是
$$\hat{a}=\vec{a}/||\vec{a}||$$
单位向量通常只用来表示方向
6、向量相加
几何上向量相加有两种表示分别是平行四边形法则和三角形法则。

平行四边形法则：对于向量a，b分别平移a和b使a，b围成一个平行四边形，这个平行四边形的对角线就是向量a+b.

三角形法则：将向量b向右平移与向量a首尾相交，连接向量a的开始点和向量b的结束点所形成的向量就是向量a+b，这对于多个向量的相加同样适用。
7、再笛卡尔坐标系中表示向量

xy通常是单位向量
用坐标表示向量时通常表示为列向量
$$A\left(\begin{array}{c}x\\ y\end{array}\right)$$
可以对向量进行转置变为行向量
$$A^T=(x,y)$$
也可以用坐标表示向量的长度
$$||A||=\sqrt{x^2+y^2}$$
8、向量的点乘
$$\vec{a}\cdot \vec{b}=||\vec{a}||||\vec{b}||cos\theta$$
也可以对计算公式变化得到计算这两个向量夹角余弦的公式
$$cos\theta =\frac{\vec{a}\cdot \vec{b}}{||\vec{a}||||\vec{b}||}$$
点乘满足交换、结合、分配律

点乘也可以再笛卡尔坐标系中表示,即对应的元素相乘再相加
$$\vec{a}\cdot \vec{b}=\left(\begin{array}{c}{x}_a\\ y_a\end{array}\right)\cdot \left(\begin{array}{c}{x}_b\\ y_b\end{array}\right)=x_a{y}_a+x_b{y}_b$$
在几何上，点乘可以使一个向量投影到另一个向量上

对于向量bperp是向量b在向量a上的投影，所以向量bperp一定沿着向量a那么就有
$$\overrightarrow{b_{\perp }}=k\vec{a}$$
其中k代表向量b在向量a上投影的长度，根据角θ可以得出
$$k=||\vec{b}||cos\theta$$
或者所以根据点乘的公式得出
$$k=\frac{\vec{a}\cdot \vec{b}}{||\vec{a}||}$$
点乘可以测量两个向量的距离，两个向量之间的距离却大他们点乘的结果越小，结果为0时两个向量垂直结果为1时两个向量重合
向量的点乘可以分解任意一个向量

对于图中的向量a就可以用点乘求出他在向量b和c上的投影向量，这两个投影向量的和就是向量a
向量点乘还可以判断两个向量的朝向是否相同

图中向量a和向量b方向相同所以向量a点乘向量大于零，但向量a和向量c方向相反，所以点乘的值就小于零
8、向量的叉乘
$$\vec{a}\times \vec{b}=-\vec{b}\times \vec{a}$$
$$\vec{a}\times \vec{b}=||\vec{a}||||\vec{b}||sin\theta$$
$$\vec{a}\times \vec{a}=\vec{0}$$
两个向量叉乘的结果分别垂直于这两个向量。
可以用右手定则判断向量叉乘结果的方向
可以用
$$\vec{x}\times \vec{y}=\vec{z}$$
来定义右手坐标系
如果
$$\vec{x}\times \vec{y}=-\vec{z}$$
那么就是左手坐标系
向量的叉乘不满足交换律，但满足结合律和分配律
在代数中表示叉乘为
$$\vec{x}\times \vec{y}=\left(\begin{array}{c}{x}_a\\ y_a\\ z_a\end{array}\right)\times \left(\begin{array}{c}{x}_b\\ y_b\\ z_b\end{array}\right)=\left(\begin{array}{c}{y}_a{z}_b-y_b{z}_a\\ z_a{x}_b-z_b{x}_a\\ x_a{y}_b-x_b{y}_a\end{array}\right)$$
叉乘可以判断两个向量的左右关系

如上图，向量a在向量b的左边，向量a叉乘向量b的值小于零，而向量b在向量a的右边，向量b叉乘向量a大于零由此可得
$$\vec{a}\times \vec{b}>0那么\vec{a}在\vec{b}的右侧$$
$$\vec{a}\times \vec{b}<0那么\vec{a}在\vec{b}的左侧$$
向量的叉乘也可以有用来判断一个点是否在一个三角形的内部

当点p在三角形abc内部时，向量AB叉乘向量AP一定d大于零，向量BC叉乘向量BP一定大于零，向量CA叉乘向量CP一定大于零，而当三角形ABC变为三角形ACB时，这些叉乘结果就变成小于零，所以要判断一个点是否在一个三角形内只要判断叉乘结果是否恒一致，也就是一直小于零或者一直大于零。
9、利用点乘和叉乘定义坐标系
$$||\vec{u}||=||\vec{v}||=||\vec{w}||$$
$$\vec{u}\cdot \vec{v}=\vec{v}\cdot \vec{w}=\vec{u}\cdot \vec{w}=0$$
$$\vec{u}\times \vec{v}=\vec{w}$$
然后可以把任何一个向量分解到这三个轴向上
$$\vec{o}=(\vec{p}\cdot \vec{u})\overrightarrow{(}u)+(\vec{p}\cdot \vec{v})\overrightarrow{(}v)+(\vec{p}\cdot \vec{w})\overrightarrow{(}w)$$

三、矩阵

1、矩阵本质上一个数字数组,形如
$$\left(\begin{array}{cc}a& b\\ c& d\\ e& f\end{array}\right)$$
2、矩阵乘积：(M × N)(N × P) = (M × P)
3、矩阵不满足交换律但是满足结合律
4、对于向量可以看作成(M×1)的矩阵
5、矩阵的转置
$${\left(\begin{array}{cc}a& b\\ c& d\\ e& f\end{array}\right)}^T=\left(\begin{array}{ccc}a& c& e\\ b& d& f\end{array}\right)$$
$$(AB{)}^T=B^T{A}^T$$
6、单位矩阵
形如
$$I=\left(\begin{array}{ccccc}1& & 0& & 0\\ 0& & 1& & 0\\ 0& & 0& & 1\end{array}\right)$$
的矩阵叫做单位矩阵
7、逆矩阵
$$A{A}^{-1}=I$$

$$(AB{)}^{-1}=B^{-1}{A}^{-1}$$
8、向量点乘和叉乘的矩阵形式
点乘
$$\vec{a}\cdot \vec{b}={\vec{a}}^T\vec{b}=(x_a,y_a,z_a)\left(\begin{array}{c}{x}_b\\ y_b\\ z_b\end{array}\right)=x_a{x}_b+y_a{y}_b+z_a{z}_b$$
叉乘
$$\vec{a}\times \vec{b}=A^{\ast }B=\left(\begin{array}{ccccc}0& & -z_a& & y_a\\ z_a& & 0& & -x_a\\ -y_a& & x_a& & 0\end{array}\right)\left(\begin{array}{c}{x}_b\\ y_b\\ z_b\end{array}\right)$$

Lecture3 变换

一、二维变换

1、缩放

将图像缩放s倍，图像缩放后的坐标(x’,y’)写作：
x’ = sx
y’ = sy
可以写作矩阵形式：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ccc}s& & 0\\ 0& & s\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

2、反射

将图像由x轴镜像，得到的坐标(x’,y’)写作：
x’ = -x
y’ = y
写作矩阵形式：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ccc}-1& & 0\\ 0& & 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

3、切变

切变效果如图，相当于把上面的边向右拽出一段距离，设距离为a

得到的坐标(x’,y’)可以表示为:
x’ = x+ay
y’= y
写作矩阵形式：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ccc}1& & a\\ 0& & 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

4、旋转

如图，正方形绕原点旋转了θ度，推导旋转的矩阵形式。

设旋转矩阵为
$$\left[\begin{array}{ccc}a& & b\\ c& & d\end{array}\right]$$
从图中可以看出：
点(1,0)变为(cosθ,sinθ)
点(0,1)变为(-sinθ,cosθ)
根据这两个条件有：
$$\left[\begin{array}{ccc}a& & b\\ c& & d\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]=\left[\begin{array}{c}cos\theta \\ sin\theta \end{array}\right]$$
$$\left[\begin{array}{ccc}a& & b\\ c& & d\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right]$$
由此得出
$$R_{\theta }=\left[\begin{array}{ccc}cos\theta & & -sin\theta \\ sin\theta & & cos\theta \end{array}\right]$$
补充
已知旋转θ角度的公式如下
$$R_{\theta }=\left[\begin{array}{ccc}cos\theta & & -sin\theta \\ sin\theta & & cos\theta \end{array}\right]$$
当旋转-θ角度时：
$$R_{-\theta }=\left[\begin{array}{ccc}cos-\theta & & -sin-\theta \\ sin-\theta & & cos-\theta \end{array}\right]=\left[\begin{array}{ccc}cos\theta & & sin\theta \\ -sin\theta & & cos\theta \end{array}\right]=R_{\theta }^T$$
可以看出旋转-θ角度的矩阵是旋转θ角度的矩阵的转置，同时旋转-θ角度的矩阵和旋转θ角度的矩阵互逆，即：
$$R_{-\theta }=R_{\theta }^{-1}=R_{\theta }^T$$
这种转置之后和他的逆相同的矩阵称之为正交矩阵

5、线性变换

线性变换，变换后坐标(x’,y’)可以写作x’=ax+by，y’ = cx+dy
即:
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ccc}a& & b\\ c& & d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

6、齐次坐标

(1)、平移

把图像向x和y放向分别平移tx和ty个单位得到坐标(x’,y’)则有:
$$\begin{gathered} x^{\prime }=x+t_x \\ {y}^{\prime }=y+t_y \end{gathered}$$
可以看出平移不是线性变换
将线性变换和平移放在同一个式子中表示
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ccc}a& & b\\ c& & d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$$

(2)、齐次坐标

为了把平移和线性变换都放在同一个矩阵中表示，我们可以给二维坐标点添加一个w写作:
$$\left[\begin{array}{c}x\\ y\\ w\end{array}\right]$$
用w等于0表示向量
用w等于1表示点
其中向量的w为0因为向量具有平移不变性
这样就可以用矩阵来表示平移变换：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\end{array}\right]=\left[\begin{array}{ccccc}1& & 0& & t_x\\ 0& & 1& & t_y\\ 0& & 0& & 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x+t_x\\ y+t_y\\ 1\end{array}\right]$$
$$\left[\begin{array}{c}x\\ y\\ w\end{array}\right]所表示的是一个点因为它可以让每个项都除以w得到\left[\begin{array}{c}x/w\\ y/w\\ 1\end{array}\right](w\ne 0)$$

7、仿射变换

平移和线性变换统称仿射变换可以写作
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccccc}a& & b& & t_x\\ c& & d& & t_y\\ 0& & 0& & 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

(1)、缩放

$$S=\left[\begin{array}{ccccc}{s}_x& & 0& & 0\\ 0& & s_y& & 0\\ 0& & 0& & 1\end{array}\right]$$

(2)、旋转

$$S=\left[\begin{array}{ccccc}cos\theta & & -sin\theta & & 0\\ sin\theta & & cos\theta & & 0\\ 0& & 0& & 1\end{array}\right]$$

(3)、平移

$$\left[\begin{array}{ccccc}1& & 0& & t_x\\ 0& & 1& & t_y\\ 0& & 0& & 1\end{array}\right]$$

8、变换合成与分解

(1)、合成变换

变换的顺序会影响变换的结果
矩阵没有交换律但满足结合律，可以将多个变换矩阵先合并计算为一个矩阵然年后在把这个矩阵应用到向量上。
$$A_n(...A_2(A_1(\vec{x})))=A_n...A_2{A}_1(\vec{x})$$

(2)、分解变换

如何分解在任意点旋转的变换
首先将旋转点平移到原点，然后进行旋转，最后在平移回原位置
$$T_c\cdot R_{\alpha }\cdot T_{-c}$$

lecture4 变换二

一、三维变换

1、三维空间的齐次坐标

3D点(x,y,z,1)
3D向量(x,y,z,0)
(x,y,z,w)w≠0如果w不等于1测该点为(x/w,y/w,z/w,1)
两个点相加表示这两个点的中点

2、三维空间变换矩阵

缩放
$$S=\left[\begin{array}{ccccccc}{s}_x& & 0& & 0& & 0\\ 0& & s_y& & 0& & 0\\ 0& & 0& & s_z& & 0\\ 0& & 0& & 0& & 1\end{array}\right]$$
平移
$$T=\left[\begin{array}{ccccccc}1& & 0& & 0& & T_x\\ 0& & 1& & 0& & T_y\\ 0& & 0& & 1& & T_z\\ 0& & 0& & 0& & 1\end{array}\right]$$
旋转
旋转分别沿着x,y,z轴表示
$$\begin{gathered} R_x(\theta )=\left[\begin{array}{ccccccc}1& & 0& & 0& & 0\\ 0& & cos\theta & & -sin\theta & & 0\\ 0& & sin\theta & & cos\theta & & 0\\ 0& & 0& & 0& & 1\end{array}\right] \\ {R}_y(\theta )=\left[\begin{array}{ccccccc}cos\theta & & 0& & sin\theta & & 0\\ 0& & 1& & 0& & 0\\ -sin\theta & & 0& & cos\theta & & 0\\ 0& & 0& & 0& & 1\end{array}\right] \\ {R}_z(\theta )=\left[\begin{array}{ccccccc}cos\theta & & -sin\theta & & 0& & 0\\ sin\theta & & cos\theta & & 0& & 0\\ 0& & 0& & 1& & 0\\ 0& & 0& & 0& & 1\end{array}\right] \end{gathered}$$
因为x×y=z，y×z=x，而x×z=-y所以沿着y轴的旋转与其他两个有所不同
绕任意轴的旋转公式
对于任意旋转可以拆分成在xyz三个轴向上的旋转
$$R_{xyz}(\alpha \beta \gamma )=R_x(\alpha )R_y(\beta )R_z(\gamma )$$
推导罗德里格斯旋转角公式
$$R(n,\alpha )=cos(\alpha )I+(1-cos(\alpha ))n{n}^T+sin(\alpha )\underset{\text{N}}{\underbrace{\left(\begin{array}{ccccc}0& & -n_z& & n_y\\ n_z& & 0& & -n_x\\ -n_y& & n_x& & 0\end{array}\right)}}$$
补充：四元数

二、视图变换和投影变换

1、视图/相机变换

(1)、如何拍摄相片

搭建场景(模型变换)
找到一个角度(视图变换)
拍摄(投影)
简称MVP变换

(2)、如何确定相机的摆放

位置向量e
看向的方向单位向量g
向上方向单位向量t

(3)、变换的特点

如果相机与所有的物体一起移动结果不变，所以可以将相机固定在一个位置上。
将相机固定到原点，向上方向为y，看向-z方向
如何将任意位置相机变换到固定位置
$$定义M_{view}使任意位置相机变换到固定位置$$
首先将位置变换到原点，然后将单位向量g旋转到-z上，将单位向量t旋转到y上
$$\begin{gathered} 可以将M_{view}分解为两步 \\ {M}_{view}=R_{view}{T}_{view} \end{gathered}$$
首先平移矩阵可以写作
$$T_{view}=\left[\begin{array}{ccccccc}1& & 0& & 0& & -x_e\\ 0& & 1& & 0& & -y_e\\ 0& & 0& & 1& & -z_e\\ 0& & 0& & 0& & 1\end{array}\right]$$
然后将单位向量g旋转到-z上，将单位向量t旋转到y上。
因为比较难以求解将任意轴旋转到坐标轴上，所以我们可以先计算将坐标轴旋转到任意轴的矩阵
$$R_{view}^{-1}$$
在对这个矩阵求逆就可以算出将任意轴旋转到坐标轴的矩阵
$$R_{view}^{-1}=\left[\begin{array}{ccccccc}{x}_{g\times t}& & x_t& & x_{-g}& & 0\\ y_{g\times t}& & y_t& & y_{-g}& & 0\\ z_{g\times t}& & z_t& & z_{-g}& & 0\\ 0& & 0& & 0& & 1\end{array}\right]$$
因为旋转矩阵使正交矩阵，所以这个矩阵的逆就是他的转置所以:
$$R_{view}=\left[\begin{array}{ccccccc}{x}_{g\times t}& & y_{g\times t}& & z_{g\times t}& & 0\\ x_t& & y_t& & z_t& & 0\\ x_{-g}& & y_{-g}& & z_{-g}& & 0\\ 0& & 0& & 0& & 1\end{array}\right]$$
虎书补充

2、投影变换

(1)、正交投影

简单理解
相机在原点看向-z向上为y，直接丢掉z坐标，将结果缩放到[-1,1]²

标准说法
映射一个立方体([l,r]×[b,t]×[f,n])到一个标准立方体上[-1,1]³

首先将立方体中心移动到原点，然后将立方体的边长缩放为2写作矩阵形式为:
$$M_{ortho}=\left[\begin{array}{ccccccc}\frac{2}{l-r}& & 0& & 0& & 0\\ 0& & \frac{2}{t-b}& & 0& & 0\\ 0& & 0& & \frac{2}{n-f}& & 0\\ 0& & 0& & 0& & 1\end{array}\right]\left[\begin{array}{ccccccc}1& & 0& & 0& & -\frac{l+r}{2}\\ 0& & 1& & 0& & -\frac{t+b}{2}\\ 0& & 0& & 1& & -\frac{n+f}{2}\\ 0& & 0& & 0& & 1\end{array}\right]$$
因为看向-z方向所以近的值大于远的值

(2)、透视投影

回顾
对于点(x,y,z,1)乘以任何非零系数k(kx,ky,kz,k)结果还是原来的点，同样这个系数也可以使z。
如何进透视投影
首先挤压一个四棱锥到一个长方体上(n→n,f→f),然后对这个长方体进行正交投影。

首先挤压这个四棱锥到长方体上
这个矩阵，使四棱锥挤压前后近平面保持不变，远平面中心点不变，远平面z值不变。
$$M_{persp⟹ortho}$$
从侧面观察挤压的过程：

根据相似三角形：
$$\frac{n}{z}=\frac{y^{\prime }}{y}⟹y^{\prime }=\frac{n}{z}y$$
同理，从上方观察这个挤压过程可得:
$$\frac{n}{z}=\frac{x^{\prime }}{x}⟹x^{\prime }=\frac{n}{z}x$$
现在就找到了y‘与y的关系，x’与x的关系其中z代表四棱锥空间内任意点的z值。
所以对于四棱锥上的任一点(x,y,z,1)挤压过后的点为:
$$\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)\stackrel{挤压}{\Rightarrow }\left(\begin{array}{c}\frac{nx}{z}\\ \frac{ny}{z}\\ Unknow\\ 1\end{array}\right)\stackrel{各项乘以z点不变}{=}\left(\begin{array}{c}nx\\ ny\\ Unknow\\ z\end{array}\right)$$
由此可以求出矩阵的一部分：
$$\left[\begin{array}{ccccccc}n& & 0& & 0& & 0\\ 0& & n& & 0& & 0\\ ?& & ?& & ?& & ?\\ 0& & 0& & 1& & 0\end{array}\right]$$
因为对于任何近平面上的点在挤压前后都保持不变所以有:
$$\left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)\stackrel{挤压}{\Rightarrow }\left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)\stackrel{各项乘以n点不变}{=}\left(\begin{array}{c}nx\\ ny\\ n^2\\ n\end{array}\right)$$
所以挤压矩阵的第三行与任意近平面上的点，点乘的结果应该是n²，因为x和y使近平面上的任意点，而点乘的结果与x和y无关所以，挤压矩阵的第三行的前两项都为0，设后两项为A，B。
$$(0,0,A,B)\cdot \left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)=n^2\stackrel{计算得}{=}An+B=n^2$$
同时在挤压时远平面f的z也保持不变，例如远平面的中心点:
$$\left(\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right)\stackrel{挤压}{\Rightarrow }\left(\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right)\stackrel{各项乘以f点不变}{=}\left(\begin{array}{c}0\\ 0\\ f^2\\ f\end{array}\right)$$
同理：
$$(0,0,A,B)\cdot \left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)=f^2\stackrel{计算得}{=}Af+B=f^2$$
因为n和f都是已知的确定值，所以A和B都可以用n和f表示出来
$$\begin{gathered} An+B=n^2 \\ Af+B=f^2 \end{gathered}$$
可以得出A=n+f,b=-nf
所以挤压矩阵就求解完成:
$$M_{persp⟹ortho}=\left[\begin{array}{ccccccc}n& & 0& & 0& & 0\\ 0& & n& & 0& & 0\\ 0& & 0& & n+f& & -nf\\ 0& & 0& & 1& & 0\end{array}\right]$$
然后对这个长方体进行正交投影
$$M_{persp}=M_{ortho}{M}_{persp⟹ortho}$$

Lecture5 光栅化一

一、透视投影补充

1、视角和长宽比

在n和f已知的情况下如何定义一个视椎。
通常情况下使用视角(field-of-view)和长宽比(aspect ratio)来定义一个视椎（假定对称，l = -r，b = -t），从相机出发看向近平面，可以给这个平面定义一个宽高比，然后定义一个视角表示可以看到的角度的范围（有时视角是垂直可视角度，有时是水平可视角度，二者可以互相转换）
在已知长宽比和视角的情况下如何计算l,r,b,t

从侧面观察透视投影可以得出
$$tan\frac{fovy}{2}=\frac{t}{|n|}$$
$$aspect=\frac{r}{t}$$

二、光栅化

1、屏幕变换

在MVP变换完成后将得到一个[-1,1]³的立方体，现在需要将其画到屏幕上。

(1)、什么是屏幕

• 一个二维数组
• 数组的大小叫做分辨率
• 一种典型的光栅化设备

(2)、Raster

• Raster德语中的屏幕
• Rasterize 画到屏幕上

(3)、pixel

• picture element的缩写
• 一个有统一颜色的小方块
• 颜色是由红绿蓝混合实现

(4)、屏幕变换

首先建立一个屏幕坐标系

• 像素的坐标是(x,y)用整数描述
• 像素的坐标范围是从(0,0)到(width-1,height-1)
• 每个像素的中心是(x+0.5,y+0.5)
• 整个屏幕的覆盖范围是(0,0)到(width,height)
  把标准立方体转换到屏幕空间

保持z不变
用一个矩阵吧(x,y)从[-1,1]²转换到[0,width],[0,height]
$$M_{viewport}=\left[\begin{array}{ccccccc}\frac{width}{2}& & 0& & 0& & \frac{width}{2}\\ 0& & \frac{height}{2}& & 0& & \frac{height}{2}\\ 0& & 0& & 1& & 0\\ 0& & 0& & 0& & 1\end{array}\right]$$

2、光栅化

将光栅化三角形变为像素

(1)、三角形网格

• 最基础的多边形
• 其他多边形都可以转换成三角形
• 一定是一个平面
• 内外定义清晰
• 三角形在明确顶点后易于差值

(2)、采样

在某一点对函数求值就是采样，通过采样可以离散化一个函数。

for (int x = 0; x < xmax; ++x)
	output[x] = f(x);

在图形学中采样是一个核心概念，可以对时间(1d)，区域(2d)，方向(2d)，体积采样(3d)。
光栅化是一个2D采样
光栅化采样每个像素中心，判断其是否在三角形内部


顶一个二进制函数:inside(tri,x,y)判断输入的点(x,y)是否在输入的三角形中，若在三角形中则返回1若不在三角形中则返回0

for (int x = 0; x < xmax; ++x)
for (int y = 0; y < ymax; ++y)
image[x][y] = inside(tri,
x + 0.5,
y + 0.5);

(3)、使用叉积判断像素中点是否在三角形内部

如果一个点恰好落在三角形的边上，可以自行判断内外部。

(4)、Bouding Box

是否要对整个屏幕进行采样？

可以使用一个包围盒(Bounding box)
取三角形三个点的x的最小和最大，y的最小和最大行程一个长方形，对长方形区域内的点进行采样。
Incremental Triangle Traversal

可以对三角形最靠近左下角的点开始采样然后向上一行从左向右采样，直到遇到三角形边界然后继续向上重复操作，适用于较细且旋转的三角形

Lecture6 光栅化二

一、Artifacts

Sampling Artifacts（在图形学中一切看上去有问题的结果）

1、采样所产生的Artifacts

（1）锯齿

（2）摩尔纹

（4）车轮现象

2、原因

信号变化速度过快以至于采样跟不上信号的变化速度

3、处理方法

在采样之前模糊图像

二、频域（Frequency Domain）

1、Sin和Cos波函数

对于cosax函数，x前面的系数决定函数变化的频率也就是函数变化的快慢，函数的周期是频率的倒数。

2、傅里叶变换

（1）傅里叶级数展开

概念：任何一个周期函数都可以写作一系列正弦和余弦的线性组合以及一个常数项。

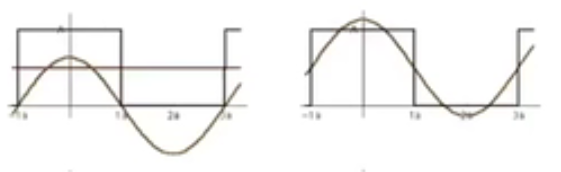
$$f(x)=\frac{A}{2}+\frac{2Acos(tw)}{\pi }$$
对于途中黑色的函数，用傅里叶级数展开近似这个函数。

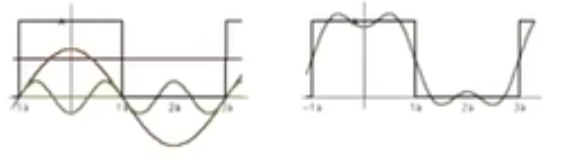
$$f(x)=\frac{A}{2}+\frac{2Acos(tw)}{\pi }-\frac{2Acos(3tw)}{3\pi }$$

$$f(x)=\frac{A}{2}+\frac{2Acos(tw)}{\pi }-\frac{2Acos(3tw)}{3\pi }+\frac{2Acos(5tw)}{5\pi }$$

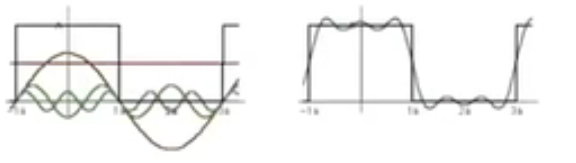
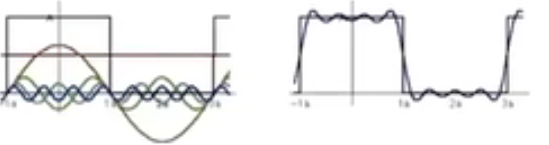
$$f(x)=\frac{A}{2}+\frac{2Acos(tw)}{\pi }-\frac{2Acos(3tw)}{3\pi }+\frac{2Acos(5tw)}{5\pi }-\frac{2Acos(7tw)}{7\pi }+...$$
通过不断的添加多项式，不断的近似原函数。

（2）傅里叶变换

给定一个函数，可以通过傅里叶变换把他变成另一个函数。
而变换出来的函数还可以通过一个逆变换把他变回原来的函数。

傅里叶变换可以把一个信号分解不同频率的段

3、从频率角度理解走样

（1）高频信号需要更快的采样

用同样的采样速度采样不同频率的函数：
对于频率越高的函数，采样的结果与原信号差别越大。

对一个函数（蓝色线）用一定的频率进行采样，采样结果得到另一个函数（黑色），假设这个结果是用同样采样频率，采样的另一个函数，那么这样，对于两个不同函数，采样之后得到了相同的结果。

高频信号采样不足，错误的表现为来自低频信号，用给定的采样频率无法区分两个不同频率的函数时称为走样。

4、滤波

滤波：把某个特定频率去除

（1）可视化图像频率内容

傅里叶变换可以把时域信息变换为频域信息

中间是低频信息，四周是高频信息。

高通滤波去掉图像中的低频信息

可以得到图像中边界的信息

低通滤波去掉图像中的高频信息

得到模糊的图像

去掉过高和过低的频率信息

（2）滤波、卷积、平均

卷积

使用一个滤波对信号进行卷积，每移动一次滤波都和滤波窗口所对应的信号数据做点乘


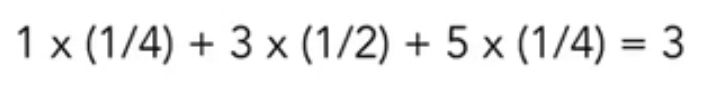
卷积定义：时域上如果想对两个信号进行卷积，对应到频域上，是这两个信号频域的乘积。
所以卷积操作可以有两个选项
选项1：直接在时域上用卷积进行滤波
选项2：用傅里叶变换把信号变换到频域上
把卷积的滤波器也变换到频域上，并把两者相乘
在用傅里叶逆变换变回时域

图中的图片在时域上做了卷积，对应到下面的频域上，使卷积。

盒式滤波

盒式滤波在时域和频域上的效果

5、从频率的角度理解采样

采样是重复频率上的内容

在时域上（左边）采样就是用冲击函数乘以原函数，得到采样后的函数。
在频域上（右边）时域上的乘积就是频域上的卷积，采样之后原始信号被重复。
采样就是重复原始信号的频谱
走样就是频域内容发生了混叠

上图是用足够的采样得到的原始函数
下图是采样不足得到的结果，频谱之间的间隔缩小，原始信号被重合，信号发生走样。

三、反走样

1、反走样解决方案

方法1、增加采样率，但这并不是反走样
方法2、真正的反走样，在重复之前让频谱更狭窄，滤除高频信息在采样之前。

图中原始信号经过一个方形虚线滤波之后，即使采用较慢的采样，也不会发生混叠。
先限制然后再重复

2、在实际的操作中如何反走样

使用一个像素宽的盒式滤波器，模糊，然后再采样。

光栅化一个三角形的时候对于求一个像素平均值的函数f(x,y)就等于求这个像素内被三角行覆盖的面积的函数inside（triangle,x, y）
MSAA（一种近似方法）

对于任何一个像素，可以先划分为几个小像素，然后求三角形覆盖小像素的数量和这个像素内所有像素的比值。
MSAA并不提高分辨率，只是一种近似方法，但会造成一些成本。
在工业上会用一些更有效的方案分布子像素，从而提高效率。
其他抗锯齿方法
FXAA（Fast Approximate AA）
TAA（Temporal AA）
超分辨率/超采样
从低分辨率到高分辨率
DLSS

Lecture7 Shading1

一、深度计算

1、画家算法

先绘制远处的物体，再绘制近处的，就可以形成正确的遮挡。

但定义单个物体的深度比较困难，当三个三角形互相遮挡，就无法定义每个三角形的距离，也就无法使用画家算法。

2、Z-buffer

存储每个像素的最小深度值，但需要额外的缓存空间。
看向-Z方向但是，距离始终是正值，值越小距离相机越近。

3、Z-buffer算法

在一开始，对于每个像设定他的深度值为无限大，再光栅化三角形时先判断当前像素的深度与z-buffer中存储的像素的大小，若小于zbuffer中存储的深度，则绘制三角形并更新zbuffer。
对于n个三角形，运算的复杂度为O(n)
绘制三角形的顺序与结果无关。

二、着色

定义：在物体上应用材质的过程
1、Blinn-Phone反射模型

输入
观察方向 V
表面法线 N
光照方向 L
表面属性（颜色，光泽度(Shininess)）
着色是局部的，仅应用于被着色的物体，所以不会在其他物体上产生阴影。
漫反射

光线被反射到各个方向
如何确定表面接受多少能量
兰伯特COS定理：光线与表面夹角的余弦，和表面接收的能量成正比。

灯光能量衰减

定义一个光源,和他距离为的单位1的球壳的强度为I，当光传播到距离为R时的能量强度与r成平方反比，为I/r²

兰伯特漫射着色模型
$$L_d=k_d(I/r^2)max(0,n\cdot l)$$

Lecture Shading2

一、着色2

tips：着色中的各种方向都是Shading Point指向光源的单位向量

1、Specular

强度与观测方向有关
对于一个无限光滑的Shading Point，他的反射方向都是他的镜面反射方向，就是入射光线对于法线方向的反射方向，对于一个比较光滑的物体，他的反射方向接近于他的镜面反射方向，观察方向接近于镜面反射方向就可以观察到高光。

观测方向接近于镜面反射方向就等于半程向量方向接近于法线方向
可以用下面的公式计半程向量方向
$$h=bisector(V,L)=\frac{v+L}{||v+L||}$$

可以用点乘测量两个向量有多接近
对于高光反射Ls就有公式
$$L_s=K_s(I/R^2)max(0,cos\alpha {)}^p$$
$$L_s=K_s(I/R^2)max(0,n\cdot h{)}^p$$
对于高光系数Ks默认都是白色

对于cos函数如下图

可以看到正常情况下，对于两个向量夹角的变化所带来的cos值的变化是非常平缓的这会导致产生的高光的面积非常大，通过提升指数P来让高光点更小，通常情况下P在100到200之间
Blinn-Phone效果展示

2、环境光照(Ambient)

假设：在所有点上环境光都一样，不依赖于任何东西
使用一个常量颜色来解释被忽视的光照(Illumination)在黑色阴影出填充颜色

他的公式是
$$L_a=K_a{I}_a$$

3、Blinn-Phone 反射模型

$$L=L_a+L_d+L_s$$
$$L=k_a{I}_a+k_d(I/r^2)max(0,n\cdot l)+k_s(I/r^2)max(0,n\cdot h{)}^p$$

二、着色频率

着色频率就是着色应用在那些点上

1、对每一个三角形着色（flat Shading）

对于每一个三角面都看做是平的，只有一个法线
可以通过三角形任意两边的叉积算出
不善于表现平滑表面

2、对每一个顶点着色（Gourand Shading）

通过插值计算三角形内部颜色
计算每个顶点的法线

3、对每一个像素着色（Phone Shading）

通过插值计算三角形内部法线
对每个像素计算着色

4、对比

着色频率：面、顶点、像素

5、如何计算逐顶点着色的顶点法线

通过四周的面法线，计算顶点法线，把四周的面法线求平均
$$N_v=\frac{{\Sigma }_i{N}_i}{||{\Sigma }_i{N}_i||}$$
对于面积相差较大的三角形可以进行加权平均来计算顶点法线

6、如何计算逐像素的法线

插值顶点法线，即可求出中间的法线，然后进行归一化
Braycentric interlplation

三、渲染管线（Graphics Pipeline）

1、Graphcis Pipeline

从三维场景变成一张二维图形中间所经历的过程，被称为渲染管线。

2、Shader Programs

在顶点和片段处理阶段进行编程
描述一个顶点或者片段的运行
比如在GLSL中写Shader只需要处理一个像素所接受的处理。
GPU可以高度并行处理数据

四、纹理映射（Texture Mapping）

1、任何一个三维物体的表面都是二维的

在表面应用纹理
如何映射一个在物体上的三角形，到纹理上。

可视化纹理坐标
每一个三角形的顶点都被指定了一个纹理坐标

2、质心坐标

插值：已知三角形三个顶点的任意属性，如何在三角形内部生成一个平滑的过渡。

Lecture9 Shading3(Texture mapping cont.)

一、纹理映射（Texture Mapping）

1、重心坐标

对三角形内部的任意属性进行插值
构建重心坐标，在三角形内部构件一个坐标系，使三角形内任意一点（x,y）都可以表示为三角形三个点的线性组合。

要满足点(x,y)在三角形内部，则αβγ都必须是非负数。

例一：A点的重心坐标

$$\begin{gathered} (\alpha ,\beta ,\gamma )=(1,0,0) \\ (x,y)=\alpha A+\beta B+\gamma C \end{gathered}$$
重心坐标也可以通过面积比求出

每个点的对应面积是与他不相邻的三角形的面积

三角形重心的重心坐标是什么

重心坐标的一般计算公式

通过三角形内部的任意一个点的重心坐标，就可以插值任意一个属性

但是重心坐标不能保证在投影前后保持不变
三维空间中的属性要在三维空间中进行插值

2、应用纹理

采样贴图映射漫反射颜色
对于一个已经光栅化的屏幕采样点(x,y)：（U,V）等于纹理坐标在点(xy)处的颜色。

纹理放大
如果纹理太小怎么办
在纹理上的一个像素叫做 Texel（纹素）

当把一个小纹理映射到高分辨率的屏幕上时，用于纹理查找的坐标可能是一个非整数，如果简单的四舍五入就是Nearest方法。
Nearest效果

Bilinear Interpolation（双线性插值）

首先找到距离这个点最近的四个点
连接四个点建立坐标系，找到采样点与左下角点之间的水平和竖直距离，s和t

定义线性插值lerp
lerp（x,v0,v1）=v0+x(v1-v0)
用水平的值s对上下两条平行的边所对应的点的颜色分别进行插值得到u0和u1

然后用竖直的值t对u0和u1这两个点进行插值就得到采样点所对应的颜色了

Bilinear的效果

Bicubic
取周围临近的16个点

Bicubic效果

纹理缩小
如果纹理过大
同样大小的像素，纹理距离越远像素所覆盖的纹理的面积越大

当像素覆盖纹理很小时，像素的颜色就是插值所得出的颜色。
但当像素覆盖的纹理过大时，还使用像素中心纹理上查找颜色，就会出现问题。
可以用超采样，增加每个像素样本的方式计算，但代价过大。
产生走样的原因，信号变化过快，采样频率跟不上信号变化的频率
如果避免采样？
（点查询问题和范围查询问题）Range Query
如何能知道纹理上任何一个区域的平均值
MipMap
快速、近似、正方形、的范围查询

给定一个图，生成他的mipmap，所产生的的额外存储量是原图的三分之一

计算mipMap细节层级
首先计算屏幕空间上的像素所覆盖的纹理空间的面积的大小，如下图计算00点所代表的的像素在纹理上的面积。

首先取该点右边和上边的点，然后找到在纹理空间上对应的点，如下图。

因为在屏幕空间上该店和上方右方的点的距离都是每个像素的边长，而且考虑到纹理空间出现的误差，计算00点和另外两个 点之间距离的最大值就可以近似每个像素在纹理上覆盖面积的边长L，进而求出面积$$L=max(\sqrt{（\frac{du}{dx}{)}^2+（\frac{dv}{dx}{）}^2},\sqrt{（\frac{du}{dy}{)}^2+（\frac{dv}{dy}{）}^2})$$
如何根据像素面积选用MipMap
可以通过计算边长为L的区域在纹理上的面积，变为1x1时所对应的MipMap的层数，就是该像素应该选用的MipMap
$$D={\log }_{2}L$$
可视化MipMap

可以发现MipMap查询结果不连续
在Mipmap变化的地方可能出现接缝，想要的到一个平滑过渡的结果。
首先分别取向上和向下的整数层，做双线性插值得出两个结果，然后在层与层之间再做一次双线性插值，这叫做三线性插值(Trilinear interpolation)
MipMap的限制

超采样结果

MipMap的结果

Mip在远处模糊到一起，出现了OverBlur
各向异性过滤
可以通过各向异性过滤（Anisotropic Filtering）解决
原本的MipMap只生成正方形的图片，如果分别在U和V方向压缩，得到两个方向上的压缩的纹理RipMaps。
规则的像素在纹理上的映射可能是不规则的

像素映射的区域与正方形差别越大，所产生的的误差也就越大。（OverBlur）
对于映射为矩形的区域可以用各向异性过滤结果，但对于图中斜着的区域便无法解决。

EWA过滤
多次查询
加权平均
MipMap层级依然有帮助
能够处理不规则的映射

Lecture 10Geometry 1

一、纹理应用

在现代GPU中纹理就是一块内存加上滤波（Memory+range Query filter）

1、Environment Map

环境光可以记录在球面上。
Spherical Environment Map

把记录在球面上的环境光展开spherical map，但在上下区域，会出现扭曲。

Cube Map
仍然使用球体记录光照信息，但在存储时记录沿球体表面的法线和球体外面包裹的立方体相交的点的信息，存储为立方体贴图，这样产生较小的扭曲。

2、纹理影响着色

凹凸贴（Bump Mapping）
定义模型表面任意一个点的相对高度，从而影响法线，给网格添加假的细节。
扰动每个像素的法线
纹理定义了每个像素高度的位移

如何修改顶点法线，对于点p会因为高度贴图，产生高度位移。

如何计算p点位移之后的法线

考虑一个简单的情况(In flatland)
有一个平面他的法线是(0,1)，产生位移后如图所示

可以通过差分计算任意一个点的切线dp = c*[h(p+1)-h§]
把切线逆时针旋转90°并归一化就是法线。
所以可以计算出法线np=(-dp,1)
在3d环境中
假设一个点的法线是np=(0,0,1)
纹理有U和V两个方向上的变化，可以计算两个切线
$$\begin{gathered} dp/du=c_1\ast [h(u+1)-h(u)] \\ dp/dv=c_2\ast [h(v+1)-h(v)] \end{gathered}$$
计算两个切线之后，法线可以表示为n = (-dp/du,-dp/dv,1)然后归一化
现在所有的计算都是在局部空间
位移贴图置换贴图
对顶点产生实际的位移。

3、三维程序纹理噪波

通过函数，计算三维空间中任何一个点的噪波。

4、记录预计算的着色

5、三维纹理和体积渲染

二、几何

1、隐式和显式几何(Implicit,Explicit)

Implicit
隐式几何的点满足一个特定的式子
比如球体可以表示为x²+y²+z² = r
通常情况下满足f(x,y,z) = 0，的所有点，所表示的几何体。
但仅仅通过公式很难判断所代表的的模型的外观
比如
$$f(x,y,z)=(2-\sqrt{x^2+y^2}{)}^2+z^2-1$$
它所代表的几何形体是一个圆环，但从公式很难判断。

但隐式几何可以很容易的判断某一个点是否在这个几何表面上。
Explicit
直接给出顶点位置或者通过参数映射所定义的表面
比如：
通过把二维的信息映射到三维而得到几何形体

显式的表示方式很容易找到所有的对应点，而隐式的方式很找到所有点

但判断一个点与表面的关系就很难判断
没有最好的几何表示方案。

2、更多的隐式几何的表示方法

简单表面代数方式

复杂表面
CSG（Constructive Solid Geometry）
通过boolean合隐式几何体

Distance Functions
不描述表面本身，描述任何一个点到这个表面的距离
混合运动边界


Level Set Methods水平集表示方式

三维空间中同样也可以应用水平集

分型
表现自身的相似性，在所有的刻度下都有这种细节

Lecture11 Geometry 2（Curves and Surfaces）

一、显式几何

1、显示几何表现方式

三角形（Triangle meshes）
贝塞尔曲面（Bezier Surrfaces）
细分曲面（subdivision surfaces）
nurbs
点云（point cloud）

点云
点坐标的列表
扫描的原始数据

多边形面
在图形学中如何表示三角形面，WaveFront Object File（.obj），把多边形的每个顶点的各种数据以文本的形式分别存储,最后定义这些顶点的连接关系

2、Curves

bezier Curves

a.de Casteljan 算法（给定点如何计算贝塞尔曲线）

考虑给定的三个控制点所生成的贝塞尔曲线，称为Quadratic Bezier（二次贝塞尔）

使用线性插值计算
图中给定的三个点b0,b1,b2其中b0和b2决定了曲线的开始和结束点，b1决定了曲线弯曲向哪一个方向，假设这个曲线的起点在时间0，重点在时间1如下图

求这条曲线就变成了求这个曲线在任意时间t时，对应的曲线上的点在空间中的位置。

首先求出时间t占整个0到1之间长度的比例，然后在b0和b1之间找到相同比例的点b01,即：使
$$t/1=|b_{0}t|/b_0{b}_1$$

然后在b1b2上也找到相同的点b11

然后连接b01和b11，在b01b11上也找到相同的点b02

最后找到的点b02就是这个曲线在时间t时，曲线上的点在空间中的位置。

把t可以看作参数，可以求出所有的点的位置，所以贝塞尔曲线时显式表示几何

对于给定四个点所定义的贝塞尔曲线，同样可以使用这种递归的方式计算曲线上的点

推导贝塞尔曲线的代数公式
考虑三点生成贝塞尔曲线的情况

用代数分别表示b01和b11
$$\begin{gathered} b_0^1(t)=(1-t)b_0+t{b}_1 \\ {b}_1^1(t)=(1-t)b_1+t{b}_2 \end{gathered}$$
然后用代数表示b02
$$b_0^2(t)=(1-t)b_0^1+t{b}_1^1$$
把这三个公式合在一起可以得到
$$b_0^2(t)=(1-t{)}^2{b}_0+2t(1-t)b_1+t^2{b}_2$$
把(1-t)看成x可以看出，这个等式和(x+t)²相似
总结：
有n+1个控制点，可以得到一个n阶的贝塞尔曲线在任意时间t上都可以写成一个给顶点的线性组合，线性组合的系数是一个与时间t有关的多项式，这个多项式称为伯恩斯坦多项式。

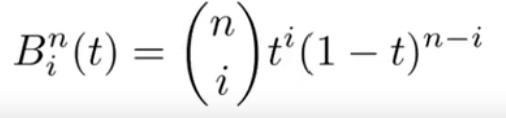
b.伯恩斯坦多项式

c.贝塞尔曲线的性质

规定了起点和终点
由控制点表示的贝塞尔曲线，如果对这些控制点进行仿射变换，变换后产生的曲线和之前的曲线是一样的。
凸包性质：曲线一定在控制点所形成的的凸包内部

凸包：能够包围一个几何体的最小的凸多边形

d.逐段贝塞尔曲线

当n为10时控制点对曲线的影响非常小，曲线变得难以控制
![[Pasted image 20220106141603.png]]

所以需要逐段的定义贝塞尔曲线然后把这些曲线连接在一起
通常使用每四个控制点为一段，

由开始点和结束点，以及两个控制杆组成
逐段贝塞尔曲线的连续性
对于两段贝塞尔曲线，只要首尾相连即是在几何上连续
这种首尾相连的连续称为c0连续

当两段贝塞尔曲线不但收尾相连，且连接点两边的点与连接点的连线方向相反且长度相等时称为一阶导数连续c1连续

3、样条线

一个连续的曲线由一系列的控制点控制，在任意一个地方满足一定的连续性
一个可控的曲线就是样条线

a.B样条

Basis Splines基函数（伯恩斯坦多项式）样条
本课程不涉及B样条的细节和NURBS（非均匀有理B样条）的内容
可以访问https://www.bilibili.com/video/BV13441127CH?p=28了解更多内容

4、曲面

a.贝塞尔曲面

扩展贝塞尔曲线称为贝塞尔曲面
在两个方向上分别应用贝塞尔曲线算法

b.推算贝塞尔曲面

对于三阶四控制点的贝塞尔曲线
输入4x4的控制点
输出一个2d平面参数[U,V]在[0,1] ^2

通过参数映射，显式表示贝塞尔曲面

5、网格操作：几何处理

网格细分
网格简化
网格规则化

Lecture12 集合3

一、网格体操作

1、网格细分

a.Loop细分（发明这个细分的人名）
首先把三角形的三个边的中点连接，分成四个三角形。

然后使新产生的顶点和老的顶点分别移动位置

对于新产生的顶点

如下图中的白点，他被上下两个三角形所共享，令他两边的点分别为A，B距他较远的点为C，D

这个白点所在的位置为:3/8(A+B) = 1/8(C+D)**

对于旧有的顶点如何更新位置
比如图中的白色顶点
首先定义n为顶点的度（Vertex Degree）即顶点所连接的线段，图中的白点的度为6
然后定义u 为当n为3时u为3/16其他情况下为3/(8n)

最后可以定义白色顶点的更新方式
(1-n*u)原位置+u周围顶点的平均位置
b.Catmull-Clark细分
loop细分只能处理三角形网格

定义四边形面和非四边形面

然后定义奇异点，即所有度不是4的点

接着进行细分操作，找到所有边的中点和面的中点并把他们连接起来

在一次细分之后，原有的非四边形面都变为了四边形边，同时产生一个新的奇异点。

接下来进行位置的更新

新产生的点分为两部分，分别是面上的点和边上的点

原有的点

2、网格体简化

a.边坍缩（edge collapsing）
如何确定哪些边可以被坍缩
Quadric Error Metrics（二次误差度量）
首先要确定简化后的点的位置

在空间中找到一个点的位置，使这个点的二次误差最小化。
二次误差：新产生的顶点和产生这个顶点的顶点的相关的面的距离的平方和
在坍缩边时，从二次度量误差最小的边开始。
计算模型所有的边被坍缩所产生的的二次度量误差

但是坍缩一条边会对他相邻的边的二次度量误差产生影响。
使用优先队列（堆）：先坍缩二次度量误差最小的的边然后动态更新他所向连的边的二次度量误差，继续取最小。

通过不断求解局部最优解来想要达到全局最优解的贪心算法，但在实际当中可以忽略

二、如何生成光栅化阴影

Shadow Mapping

一种图像空间的算法
在计算阴影的时候不需要知道场景的集合信息
会产生走样现象

如果某一个点不在阴影里面，那么从光源和从相机都应该可以看到这个点
经典的shadow maping只能处理点光源和方向光源

需要分通道渲染
通道1：从光源出发渲染每一个点的深度
通道2：从相机出发渲染每个点的深度

案例：
在左上角有一个光源

首先从光源看向场景，记录每个点的深度
然后从实际的相机看向场景，记录每个像素到光源的距离，并投影到光源所记录的深度图上，与相应的值作对比。

shadow maps问题
只能能处理硬阴影