1、简介

线性判别式分析(Linear Discriminant Analysis, LDA)，也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD)，是模式识别的经典算法，它是在1996年由Belhumeur引入模式识别和人工智能领域的。性鉴别分析的基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。因此，它是一种有效的特征抽取方法。LDA是一种有监督的算法。

2、LDA算法（二类情况）

给定特征为d维的N个样例$x^{(i)}\left\{x_1^{(i)},x_2^{(i)},\cdots ,x_d^{(i)}\right\}$，其中有$N_1$个样例属于类别${\omega }_1$，$N_2$个样例属于类别${\omega }_2$。

现在我们想将$d$维特征降到只有一维，而又要保证类别能够“清晰”地反映在低维数据上，也就是这一维就能决定每个样例的类别。这里的降维可以通过将样本点投影到一个低维平面上来实现。在这里为了简单起见，我们设样例为二维的，也就是$d=2$,并将其投影到一条方向为$w$的直线上去，这样就将2维的特征降到了1维。

样例$x$到从原点出发方向为$w$的直线上的投影可以用下式来计算：$y=w^{T}x$。注意，这里的$y$不是标签值，而是$x$投影到直线上的点到原点的距离。

我们的目的是寻找一条从原点出发方向为$w$的直线，可以将投影后的样例点很好的分离，大概如下图所示：

从直观上来讲，第二条直线看起来还不错，可以很好地将两类样例分离，那这条直线是不是我们所要找的最佳的直线呢？要回答这个问题，我们就要从定量的角度来确定最佳的投影直线，即直线的方向向量$w$。
首先求每类样例的均值（中心点）：${\mu }_i=\frac{1}{N_i}{\sum }_{x\in w_i}x$
那么投影后的每类样例的均值（中心点）为：${\tilde{\mu }}_i=\frac{1}{N_i}{\sum }_{y\in w_i}y=\frac{1}{N_i}{\sum }_{x\in w_i}{w}^{T}x=w^T{\mu }_i$

从上面两条公式可以看出，投影后的中心点就是中心点的投影。

从上面两张图可以看出，能够使投影后的两类样本中心点尽量分离的直线是好的直线，定量表示就是：${\max }_{w}J(w)=\left|{\tilde{\mu }}_1-{\tilde{\mu }}_2\right|=\left|w^T{\mu }_1-w^T{\mu }_2\right|$。但是仅仅考虑$J(w)$是不行的，如下图所示：

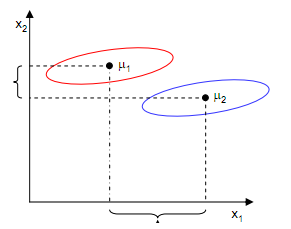
尽管在$X_1$轴上取得了中心点投影的最大间距，但是由于重叠严重，反而不能很好的分离两类样本点。中心点投影在$X_2$轴上的间距虽然很小，但是却能够取得比$X_1$轴更好的分离效果。这是为什么呢？
LDA是基于Fisher准则的算法，其必须同时遵从类内密集，类间分离这两个条件。中心点投影间距最大化只是满足类间分离而没有考虑类内密集，所以为了获得最佳的投影方向 $w$，我们还要将同一类样例的类内密集度做为一个约束，在这里，我们采用散列值 scatter作为密集度的一个度量。

每个类别的散列值定义如下：${\tilde{s}}_i^2={\sum }_{y\in w_i}{\left(y-{\tilde{\mu }}_i\right)}^2$，可以看出，散列值与方差较为接近，类内越密集，散列值越小；类内越分散，散列值越大。
有了散列值，我们得以满足Fisher准则的类内密集的要求，结合最大化中心点的投影间距，我们可以提出最终的度量公式：${\max }_{w}J(w)=\frac{{|\widetilde{{\mu }_1}-\widetilde{{\mu }_2}|}^2}{{\widetilde{s_1}}^2+{\widetilde{s_2}}^2}$
将散列值的公式展开可得：
${\widetilde{s_i}}^2={\sum }_{y\in w_i}{\left(y-{\tilde{\mu }}_i\right)}^2={\sum }_{x\in w_i}{\left(w^{T}x-w^T{\mu }_i\right)}^2={\sum }_{x\in w_i}{w}^T\left(x-{\mu }_i\right){\left(x-{\mu }_i\right)}^{T}w$
令$S_i={\sum }_{x\in w_i}\left(x-{\mu }_i\right){\left(x-{\mu }_i\right)}^T,S_w=S_1+S_2$
则${\widetilde{s_i}}^2=w^T{S}_{i}w,{\widetilde{s_1}}^2+{\widetilde{s_2}}^2=w^T{S}_{w}w$，分母部分完毕，接下来处理分子部分。
展开分子，${\left({\tilde{\mu }}_1-{\tilde{\mu }}_2\right)}^2={\left(w^T{\mu }_1-w^T{\mu }_2\right)}^2=w^T\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^{T}w$
令$S_B=\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^T$ ，则 ${\left(\widetilde{{\mu }_1}-\widetilde{{\mu }_2}\right)}^2=w^T{S}_{B}w$，分子部分完毕。
度量公式可表示为：${\max }_{w}J(w)=\frac{w^T{S}_{B}w}{w^T{S}_{w}w}$
在我们求导之前，需要对分母进行归一化，因为不做归一的话，$w$扩大任何倍，都成立，我们就无法确定$w$。因此我们打算令$\Vert w^T{S}_{w}w\Vert =1$，那么加入拉格朗日乘子后，求导:
$c(w)=w^T{S}_{B}w-\lambda \left(w^T{S}_{w}w-1\right)$
$\frac{dc}{dw}=2S_{B}w-2\lambda S_{w}w=0$
$S_{B}w=\lambda S_{w}w$
若Sw可逆，则 $S_w^{-1}{S}_{B}w=\lambda w$ ，即 $w$ 是矩阵 $S_w^{-1}{S}_B$ 的特征向量。由此可以求出$w$。
上面这个式子还可以进一步化简：
$S_{B}w=\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^{T}w=\left({\mu }_1-{\mu }_2\right)\ast {\lambda }_w$ ，这里的 ${\lambda }_w$ 是一个常数。
代入原式可得: $S_w^{-1}{S}_{B}w=S_w^{-1}\left({\mu }_1-{\mu }_2\right)\ast {\lambda }_w=\lambda w$,由于对 $w$ 扩大缩小任何倍不影响结果，因此可以约去两边的末知常数 ${\lambda }_w,\lambda$ ，
得到 $w=S_w^{-1}\left({\mu }_1-{\mu }_2\right)$ 。
上面那张图的投影结果如下图所示:

3、LDA算法（多类情况）

在二类情况下，$J(w)$的分子是两类中心距，分母是每个类自己的散列度。现在投影方向是多维了（好几条直线），分子需要做一些改变，我们不是求两两样本中心距之和（这个对描述类别间的分散程度没有用），而是求每类中心相对于全样本中心的散列度之和。除却这个变化，其他推导与二类情况相似，这里不做展开说明。

4、实例

三维投影到二维平面：($W1$相比$W2$能够获得更好的分离效果。)

PCA与LDA的降维对比：
LDA用于降维，和PCA有很多相同，也有很多不同的地方，因此值得好好的比较一下两者的降维异同点。

首先我们看看相同点：

1）两者均可以对数据进行降维。

2）两者在降维时均使用了矩阵特征分解的思想。

3）两者都假设数据符合高斯分布。

我们接着看看不同点：

1）LDA是有监督的降维方法，而PCA是无监督的降维方法

2）LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。

3）LDA除了可以用于降维，还可以用于分类。

4）LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。

这点可以从下图形象的看出，在某些数据分布下LDA比PCA降维较优。

PCA选择样本点投影具有最大方差的方向，LDA选择分类性能最好的方向。

LDA既然叫做线性判别分析，应该具有一定的预测功能，比如新来一个样例x，如何确定其类别？

拿二值分来来说，我们可以将其投影到直线上，得到$y$，然后看看$y$是否在超过某个阈值$y_0$，超过是某一类，否则是另一类。而怎么寻找这个$y_0$呢？
看
$\mathrm{y}=w^{T}x$
根据中心极限定理，独立同分布的随机变量和符合高斯分布，然后利用极大似然估计求$\mathrm{P}\left(\mathrm{y}\mid {\mathrm{C}}_i\right)$
然后用决策理论里的公式来寻找最佳的y0，详情请参阅PRML。
这是一种可行但比较繁琐的选取方法，可以看第7节（一些问题）来得到简单的答案。

5. 使用LDA的一些限制

1、 LDA至多可生成C-1维子空间
LDA降维后的维度区间在[1,C-1]，与原始特征数n无关，对于二值分类，最多投影到1维。
2、 LDA不适合对非高斯分布样本进行降维。

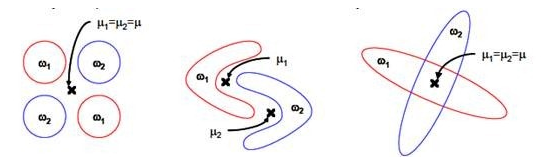
上图中红色区域表示一类样本，蓝色区域表示另一类，由于是2类，所以最多投影到1维上。不管在直线上怎么投影，都难使红色点和蓝色点内部凝聚，类间分离。

上图中，样本点依靠方差信息进行分类，而不是均值信息。LDA不能够进行有效分类，因为LDA过度依靠均值信息。
4、 LDA可能过度拟合数据。

6. LDA的一些变种

1、非参数LDA
非参数 $LDA$ 使用本地信息和K临近样本点来计算 $S_B$,使得 $S_B$ 是全秩的，这样我们可以抽取多余C-1个特征向
量。而且投影后分离效果更好。
2、正交LDA
先找到最佳的特征向量，然后找与这个特征向量正交且最大化 fisher条件的向量。这种方法也能摆脱 $C-1$ 的限 制。
3、一般化LDA
引入了贝叶斯风险等理论
4、核函数 $LDA$
将特征 $\mathrm{x}\to \Phi (\mathrm{x})$ ，使用核函数来计算。

7. 一些问题
上面在多值分关中使用的
$${\mathrm{S}}_B=\sum _{i=1}^c{N}_i\left({\mu }_i-\mu \right){\left({\mu }_i-\mu \right)}^T$$
是带权重的各关样本中心到全样本中心的散列矩阵。如果 $C=2$ (也就是二值分类时) 套用这个公式，不能够 得出在二值分尖中使用的 ${\mathrm{S}}_B$ 。
$${\mathrm{S}}_B=\sum _{i=1}^c\left({\mu }_1-{\mu }_2\right){\left({\mu }_1-{\mu }_2\right)}^T$$
因此二值分类和多值分关时求得的 ${\mathrm{S}}_B$ 会不同，而 ${\mathrm{S}}_W$ 意义是一政的。
对于二值分类问题，令人惊奇的是最小二乘法和Fisher线性判别分析是一致的。
下面我们证明这个结论，并且给出第 4 节提出的 $\mathrm{y}$ 值得选取问题。
回顾之前的线性回归，给定 $\mathrm{N}$ 个 $\mathrm{d}$ 维特征的训练样例 $x^{(i)}\left\{x_1^{(i)},x_2^{(i)},\dots ,x_d^{(i)}\right\}$ (i从1到 $\mathrm{N}$ )，每个 $x^{(i)}$ 对应一个粂 标签 $y^{(i)}$ 。我们之前令 $y=0$ 表示一类， $y=1$ 表示另一关，现在我们为了证明最小二乘法和LDA的关系，我们需要 做一些改栾
$$\{\begin{array}{l}\mathrm{y}=\frac{N}{N_1},\text{ 样例属于有 }{N}_1\text{ 个元素的类 }{C}_1\\ \mathrm{y}=-\frac{N}{N_2},\text{ 样例属于有 }{N}_2\text{ 个元素的类 }{C}_2\end{array}$$
就是将0/1做了值蔓换。
我们列出最小二乘法公式$\mathrm{E}=\frac{1}{2}{\sum }_{i=1}^N{\left(w^T{x}^{(i)}+w_0-y^{(i)}\right)}^2$
$w$ 和 $w_0$ 是拟合权重参数。
分别对 $w_0$ 和 $w$ 求导得${\sum }_{i=1}^N\left(w^T{x}^{(i)}+w_0-y^{(i)}\right)=0$
$$\sum _{i=1}^N\left(w^T{x}^{(i)}+w_0-y^{(i)}\right)x^{(i)}=0$$
从第一个式子展开可以得到
$$w^{T}N\mu +N{w}_0-\sum _{i=1}^N{y}^{(i)}=w^{T}N\mu +N{w}_0-\left(N_1\frac{N}{N_1}-N_2\frac{N}{N_2}\right)=0$$
消元后，得
可以证明第二个式子展开后和下面的公式等价
其中 $S_w$ 和 $S_B$ 与二值分关中的公式一样。
由于 $S_B\mathrm{w}=\left({\mu }_1-{\mu }_2\right)\ast {\lambda }_w$
因此，最后结果仍然是
这个过程从几何意义上去理解也就是变形后的线性回归（将类标笈重新定义），线性回归后的直线方向就是 二值分关干LDA求得的直线方向 $w$ 。
好了，我们从改变后的 $y$ 的定义可以㺺出 $y>0$ 属于关 $C_1，y<0$ 属于关籿 $C_2$ 。因此我们可以选取 $y0=0$ ，即如果 $\mathrm{y}(\mathrm{x})=w^{T}x+w_0>0$ ，就是栚 $C_1$ ，否则是猋 $C_2$ 。
写了好多，挺杂的，还有个topic模型也叫做LDA，不过名字叫做Latent Dirichlet Allocation，第二作者就 是Andrew Ng大牛，最后一个他导师Jordan泰斗了，什么时候拜读后再写篇总结发上来吧。