机器学习：贝叶斯网络

贝叶斯网络

JacksonKim

15856人浏览 · 2021-11-27 14:29:03

JacksonKim · 2021-11-27 14:29:03 发布

一、什么是贝叶斯网络？

贝叶斯网络是一种用于进行概率推理的模型。（比如说下面这个图，箭头表示因果关系，也就是强盗抢劫和地震都会引起房子铃响，如果房子铃响，那么这个人的两个邻居John和mary会打电话给他）。这里通过因果关系建立起来的网络称之为贝叶斯网络，那么它支持哪些推理呢？
在这里插入图片描述
如果我们根据先验知识构建了这个贝叶斯网络，那么我们是可以对这样一个查询进行概率推理的——如果John打电话给我，发生抢劫的概率是多少呢？

这个概率推理的过程运用到了贝叶斯公式，所以我们称之为贝叶斯网络。

二、贝叶斯网络是如何构建的？

其实这个是很trivial的，贝叶斯网络是由领域专家构建的，所有的先验概率都是根据经验统计来的。如果上述的铃响贝叶斯网络就是可以有一般具有常识的人进行构建。先验知识，e.g P(E)是根据以往发生地震的次数统计的概率（其他也是如此得到）。

三、如果根据贝叶斯网络对某个查询进行概率推理。

（一）查询的形式化表示

我们用X表示查询变量，E表示证据变量集 $E_1,E_2,...$ ，e表示证据变量的某个具体值（观察到的特定事件），Y表示非证据非查询变量集 $Y_1,Y_2,...$ (也称隐藏变量，hidden variable)。这样，全部变量的集合是 ${X}\cup E\cup Y$ .举例，比如“如果John打电话给我，发生抢劫的概率是多少呢？”这个查询，查询变量就是Burgary(用大写表示该布尔变量）=< $\neg burgary$ >, 证据变量就是johncall(用小写表示布尔变量值，这里代表true)。其他变量就是属于非证据非查询变量集。

对于查询的概率推理其实就是求后验概率 $P (X ∣ e)$ , 即已知e的情况下求X的概率。在上诉的例子中就是求P(Burgary|johncall).

（二）精确推理

1.通过枚举进行推理

什么是枚举？

通过枚举其他所有的非证据非查询变量来获得目标后验概率，如下：
$P(X|e)=\dfrac{P(X,e)}{P(e)} = \alpha P(X,e) = \alpha \sum_y P(X,e,y)$

其中y代表证据变量Y的可能取值。上述P(e)是先验概率，可用 $\alpha$ 替代。

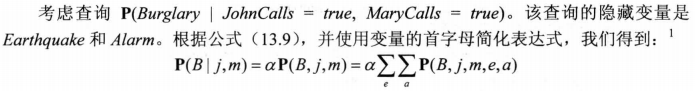
在这里插入图片描述
贝叶斯网络的语义使得上述的联合概率可以转化为一系列的条件概率和先验概率的乘积。比如Burglary=true的计算过程为：

$\mid j, m)=\alpha \sum_{e} \sum_{a} P(b) P(e) P(a \mid b, e) P(j \mid a) P(m \mid a)$

上诉表达式需要对4各项求和，而每一行对视5个数的乘积。所以这个算法对于布尔变量组成的贝叶斯网络来说时间复杂度为 $O(n2^n)$ , n是非证据非查询变量数。

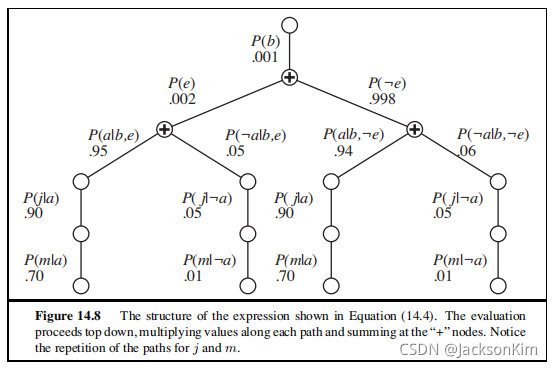
在这里插入图片描述

通过上述算法，我们可以把复杂度进一步减到 $1+2+2^{2} +...2^{n} =2^{n+1}-1=O(2^n)$

2.推理优化

（1）变量消元法
我们可以看到上面那棵树中P(m|a)实际上运算了两次，即上述递归算法存在重复计算的问题。利用动态规划的思想，我们想要以空间换时间，将某些变量的条件概率保存起来，那么就有了变量消元法：

变量消元算法的工作方式是按照从右到左的次序(也就是按照图14.8中自底向上的次序)计算诸如公式(14.4)的表达式。中间结果被保存下来,而对每个变量的求和只需要对依赖于这些变量的表达式部分进行就可以了。

（2）调整变量顺序和变量相关性

（1）中算法包含了一个不明确的 ORDER函数来选择变量的顺序。变量顺序的每种选择都会得到一个有效算法,但不同的变量顺序会在计算过程中产生不同的中间因子。

当变量不只是布尔变量时，我们优先选择变量值更少的变量，可以降低算法复杂度。

另外根据贝叶斯网络，我们可以从网络中删除一些与当前查询无关的点，因为求和之后他们的概率和为1，对概率推理的结构没有影响.比如：

在这里插入图片描述

（三）近似推理

1.为什么要近似推理

因为大规模多连通网络中的精确推理是不实际的(复杂度太高）,NP难。

2. 如何进行近似推理

使用采样方法中的统计结果模拟真实的概率值P(X|e)。这种思想（算法）称为蒙特卡洛算法。比如我们一开始提到得例子，如果John打电话给我（记为A)，发生抢劫（记为B）的概率是多少呢？如果贝叶斯网络很大，精确计算得复杂度，就会很高。那么我们依照已有得先验概率对所有变量进行采样，最后 $=\dfrac{同时包含A，B得样本}{包含A的样本}$ 。可以想见，对于大规模多联通网络，这种近似推理的方法比精确推理的复杂度要低得多。

蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

在这里插入图片描述
2.1直接采样算法
按某个变量顺序（一般是从父到子顺序）按先验概率进行采样，如上图，比如Cloudy的概率分布<0.5,0.5>，那在生成样本的时候就是一半生成为True，一半生成为False. 接下来一次对Sprinkler，Rain，WetGrass进行采样，可以得到一条样本（e.g. [true,true,false,true])。当我们得到N条样本，我们可以用相应查询变量的频率估计改查询变量的概率。例如,假设我们从草坪喷灌( sprinkler)网络生成了1000个样本,其中511个样本满足Rain=true,那么下雨的估计概率,记作P(Rain=true),就等于0.511。
在这里插入图片描述

2.2拒绝采样算法

首先，它根据网络指定的先验分布生成采样样本。然后，它拒绝所有与证据不匹配的样本。最后，在剩余样本种通过统计X=x的频次而计算出估计概率 $\hat P(X=x|e)$ 。

缺点：拒绝了太多了样本。随着证据变量个数的增多，与证据e相一致的样本在所有样本种所占的比例呈指数级下降，所以对于复杂问题不能适用。

2.3似然加权 liklihood weighting

似然加权只生成与证据e一致的事件，从而避免拒绝采样算法的低效率。它是重要性采样（importance sampling）的一般统计技术的特殊情况。

但是这里有一个问题，就是这样统计出来的概率并不是目标事件发生的概率。因为证据变量本身也存在概率分布，这里我们把证据e固定住了来进行采样，事实上概率是偏大的。

因此我们需要设置跟证据变量e概率分布相关的一个权值w，来补偿真实分布和期望采样分布之间的差距。

在估计目标事件 $\hat P(X=x|e)$ 的概率时，我们统计的是X=x的权值总和，而并不是X=x的频次。

可以证明，用似然加权抽样方法估计（似然加权估计）的概率跟精确计算的概率值是相近（一致）的。证明如下：
（1）将非证据（含查询变量）记作Z，虽然我们固定了证据变量，但是采样的时候还是根据以下的概率分布进行采样的：
$S_{W S}(\mathbf{z}, \mathbf{e})=\prod_{i=1}^{l} P\left(z_{i} \mid \text { parents }\left(Z_{i}\right)\right)$
因此，我们最后得到某一条的频数（采样结果）和这个概率分布是一致的。
（2）每一条样本的权值计算w(z,e)
$w(\mathbf{z}, \mathbf{e})=\prod_{i=1}^{m} P\left(e_{i} \mid \text { parents }\left(E_{i}\right)\right)$
(3) 我们说最后估计目标事件 $\hat P(X=x|e)$ 的概率时，我们统计的是X=x的权值总和，而并不是X=x的频次。也就是说最后统计的是相同的子事件的频次*权值（如下所示）
$\begin{aligned} \hat{P}(x \mid \mathbf{e}) &=\alpha \sum_{\mathbf{y}} N_{W S}(x, \mathbf{y}, \mathbf{e}) w(x, \mathbf{y}, \mathbf{e}) \\ & \approx \alpha^{\prime} \sum_{\mathbf{y}} S_{W S}(x, \mathbf{y}, \mathbf{e}) w(x, \mathbf{y}, \mathbf{e}) \\ &=\alpha^{\prime} \sum_{\mathbf{y}} P(x, \mathbf{y}, \mathbf{e}) \\ &=\alpha^{\prime} P(x, \mathbf{e})=P(x \mid \mathbf{e}) \end{aligned}$
这里x是查询变量，y是非证据非查询变量，e是证据变量。（x,y,e)可认为是（x,e)的子事件（因为后者是前者的全部的和）。上面这个式子就证明了用似然加权抽样方法估计（似然加权估计）的概率跟精确计算的概率值是相近（一致）的。

2.4 通过模拟马尔科夫链进行推理

在阅读本小节内容之前，强烈推荐先阅读以下内容：

LDA-math-MCMC 和 Gibbs Sampling
MCMC(一)蒙特卡罗方法
 MCMC(二)马尔科夫链
 MCMC(三)MCMC采样和M-H采样
 MCMC(四)Gibbs采样

马尔可夫链蒙特卡洛( Markov chain Monte Carlo,MCMC)算法与拒绝采样和似然加权的工作方式有很大差异。马尔可夫链蒙特卡洛算法不是白手起家生成样本,而是通过对前一个样本进行随机改变而生成样本。因此我们可把MCMC算法想象成:在特定的当前状态每个变量的取值都已确定然后随机修改当前状态而生成下一个状态。(如果这使你想起第4章的模拟退火算法或第7章的 WALKSAT,是因为它们都是MCMC算法家族的成员)。这里我们将描述一种特殊形式的MCMC算法,称为 Gibbs采样,它特别适合贝叶斯网络。

吉布斯采样的一个具体方法（下面的伪代码很难看，还是要耐心看一下）：

在这里插入图片描述
下面给出一个例子，也许会更好地理解：

考虑应用于上图a所示网络的查询P( Rain I Sprinkler=true, Wetgrass=true)。证据变量 Sprinkler和 Wetgrass固定为它们的观察值,而非证据变量 Cloud和Rain则随机地初始化一一比如,分别初始化为true和 false。因此,初始状态为[true,true, false,true]。现在,以任意顺序对非证据变量采样。例如:

1.对 Cloud采样,给定它的马尔可夫覆盖变量的当前值:在这里,我们是从P(Cloudy|Sprinkler=true,Rain=false)中采样。(我们马上会说明如何计算这个分布)。假设采样结果为Cloudy= false。那么新的当前状态是[ false,true,false,true].

2.对Rain采样,给定它的马尔可夫覆盖变量的当前值:在这里,我们是从P(Rain|Coudd=false, Sprinkler=true, Wetgrass=true)中采样。假设采样结果为Raim=true。新的当前状态是[false,true,true,true]。

这个过程中所访问的每一个状态都是一个样本,能对查询变量Rain的估计做贡献。如果该过程访问了20个Rain为真的状态和60个Rain为假的状态,则所求査询的解为NORMALI7E(20,60)=(0.25,0.75)。完整的算法如图14.16所示。

现在的一个问题是：如何证明这种采样方法推理的得到的概率 $\tilde P(x|e)$ 就近似等价于真实的 $P (x ∣ e)$
拆成两个子问题就是
（1）达到稳态的时候，生成的样本是否服从这个稳态分布？
（2）稳态分布是否就是真实分布？

四、Gibbs采样的几个问题及其解释

1.马氏链收敛定理

为了证明第一个问题，先复述下马氏链的收敛定理。

这个马氏链的收敛定理非常重要，所有的 MCMC(Markov Chain Monte Carlo) 方法都是以这个定理作为理论基础的 定理的证明相对复杂，一般的随机过程课本中也不给证明，所以我们就不用纠结它的证明了，直接用这个定理的结论就好了。（以下内容引自LDA-math-MCMC 和 Gibbs Sampling）

马氏链收敛定理：如果一个非周期马氏链具有转移概率矩阵P，且它的任何两个状态时联通的，那么 $\displaystyle \lim_{n\rightarrow\infty}P_{ij}^n$ 存在而且与i无关，记 $\displaystyle \lim_{n\rightarrow\infty}P_{ij}^n=\pi(j)$ ，我们有

$\displaystyle \lim_{n \rightarrow \infty} P^n =\begin{bmatrix} \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}$
$\displaystyle \pi(j) = \sum_{i=0}^{\infty}\pi(i)P_{ij}$
$\pi$ 是方程 $\pi P=\pi$ 的唯一非负解

其中，
$\pi = [\pi(1), \pi(2), \cdots, \pi(j),\cdots ], \quad \sum_{i=0}^{\infty} \pi_i = 1$

$\pi$ 称为马氏链的稳态分布。

$\displaystyle \pi(j) = \sum_{i=0}^{\infty}\pi(i)P_{ij}$ 可用来判断一个分布是否是稳态分布（马氏链是否一收敛）。但是我们可以用更细致的判定条件来判断：

马氏链的细致平稳条件如果非周期马氏链的转移矩阵P和分布 $\pi(x)$ 满足
$\pi(i)P_{ij} = \pi(j)P_{ji} \quad\quad \text{for all} \quad i,j$
则 $\pi(x)$ 是马氏链的稳态分布。

2. 达到稳态的时候，生成的样本服从这个稳态分布？

在这里插入图片描述
首先，我们是随机生成了一个样本（状态） $x_0$ , 它应该是属于某个随机分布。

不妨把一开始的随机生成的样本服从的分布记为 $\pi _0(x)$ ，根据马氏链定理，任意一个初始分布都会收敛到相同的稳态分布（稳态分布实际上由状态转移矩阵决定）。

那么我们第2个样本的生成是选定X的第i个非证据变量，然后依照条件概率 $P(Z_i|mb(Z_i))$ 进行采样。因此第2轮的样本第i个分量服从的分布是 $\pi _1(i)=\pi _0(i)P(Z_i)$ ，记 $\pi_1(x) = [\pi_0(1),...\pi_1(i),...\pi_0(n)]$ ，那么显然这个样本服从分布 $\pi_1(x)$

假设到第n步的时候马氏链收敛，也就是这时候采样的样本服从的分布 $\pi _n(x)$ 不再变化。这样不太变化的分布就是稳态分布。也就是生成的样本服从这个稳态分布。

现在来证明第二个问题。

3. 稳态分布是否就是真实分布？

在一般的吉布斯采样中，一般都是确定了真实分布，将稳态分布就设定为目标真实分布，然后去找该分布的状态转移矩阵。

但是在贝叶斯网中，我们是先知道了状态转移矩阵，其第i行上的元素为 $P(Z_i|mb(Z_i)$ ，那么我们来验证，这个状态转移矩阵最终达到的稳态分布是否就是我们想要的真实分布 $P (x ∣ e)$

一种证明方法是，我们把稳态分布 $\pi(x)$ 赋值为 $P (x ∣ e)$ （猜值求证法），看它是否满足细致平稳条件，如果是，又根据稳态分布的唯一性，说明最终的稳态分布 $\pi(x)$ 就是真实分布 $P (x ∣ e)$ 。

我们知道，采样器逐次以转移概率 $q_i$ 采样每个变量 $X_i$ ,转移概率 $q_i$ 以所有其他变量为条件——定义 $\bar X_i$ 为除证据变量和 $X_i$ 以外的所有其他变量;当前状态下它们的值是 $\bar x_i$ 。如果以包括证据变量在内所有其他变量为条件采样 $X_i$ 的一个新值 $x_i^{'}$ ,则有
$q_{i}\left(\mathbf{x} \rightarrow \mathbf{x}^{\prime}\right)=q_{i}\left(\left(x_{i}, \overline{\mathbf{x}}_{i}\right) \rightarrow\left(x_{i}^{\prime}, \overline{\mathbf{x}}_{i}\right)\right)=P\left(x_{i}^{\prime} \mid \overline{\mathbf{x}}_{i}, \mathbf{e}\right)$

现在我们将 $P (x ∣ e)$ 带入细致平稳条件
$\begin{aligned} \pi(\mathbf{x}) q_{i}\left(\mathbf{x} \rightarrow \mathbf{x}^{\prime}\right) &=P(\mathbf{x} \mid \mathbf{e}) P\left(x_{i}^{\prime} \mid \overline{\mathbf{x}}_{i}, \mathbf{e}\right)=P\left(x_{i}, \overline{\mathbf{x}}_{i} \mid \mathbf{e}\right) P\left(x_{i}^{\prime}\mid \overline{\mathbf{x}}_{i}, \mathbf{e}\right)\\ &=P\left(x_{i} \mid \overline{\mathbf{x}}_{i}, \mathbf{e}\right) P\left(\overline{\mathbf{x}}_{i} \mid \mathbf{e}\right) P\left(x_{i}^{\prime} \mid \overline{\mathbf{x}}_{i}, \mathbf{e}\right) \\ &=P\left(x_{i} \mid \overline{\mathbf{x}}_{i}, \mathbf{e}\right) P\left(x_{i}^{\prime}, \overline{\mathbf{x}}_{i} \mid \mathbf{e}\right) \\ &=\pi\left(\mathbf{x}^{\prime}\right) q_{i}\left(\mathbf{x}^{\prime} \rightarrow \mathbf{x}\right) \end{aligned}$