优化与深度学习

在前面的介绍中，我们的训练过程是通过对损失函数求偏导进行梯度下降的方式进行训练，以使loss的函数值降低，最终得到一个最小损失函数值，这时候的模型可以说是训练好的模型。但是对于下面的这种情况，函数值出现了局部的低点和全局的低点。

%matplotlib inline
import sys
sys.path.append('/home/kesci/input')
import d2lzh1981 as d2l
from mpl_toolkits import mplot3d # 三维画图
import numpy as np

def f(x): return x * np.cos(np.pi * x)
def g(x): return f(x) + 0.2 * np.cos(5 * np.pi * x)

d2l.set_figsize((5, 3))
x = np.arange(0.5, 1.5, 0.01)
fig_f, = d2l.plt.plot(x, f(x),label="train error")
fig_g, = d2l.plt.plot(x, g(x),'--', c='purple', label="test error")
fig_f.axes.annotate('empirical risk', (1.0, -1.2), (0.5, -1.1),arrowprops=dict(arrowstyle='->'))
fig_g.axes.annotate('expected risk', (1.1, -1.05), (0.95, -0.5),arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('risk')
d2l.plt.legend(loc="upper right")

这张图里模拟了两个函数，蓝色的函数代表训练集损失函数，紫色虚线代表测试集损失哈数。在图像上可以看到训练集损失函数的最低点和测试集的最低点并不重合。代表训练集上使误差最小的模型，不一定是测试集上最优的。
尽管优化方法可以最小化深度学习中的损失函数值，但本质上优化方法达到的目标与深度学习的目标并不相同。
最优化时，优化的是训练集误差，但深度学习是为了提高模型的泛化能力，即降低测试集上的误差。
这个道理仔细琢磨还是挺深刻的，数学里面的道理可以推广到工作和生活中。那数学中的解法能不能也用到生活中呢。

优化在深度学习中的挑战

局部最小值

看如下函数
$$f(x)=xcos(\pi x)$$

def f(x):
    return x * np.cos(np.pi * x)

d2l.set_figsize((4.5, 2.5))
x = np.arange(-1.0, 2.0, 0.1)
fig,  = d2l.plt.plot(x, f(x))
fig.axes.annotate('local minimum', xy=(-0.3, -0.25), xytext=(-0.77, -1.0),
                  arrowprops=dict(arrowstyle='->'))
fig.axes.annotate('global minimum', xy=(1.1, -0.95), xytext=(0.6, 0.8),
                  arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)')

这个曲线在左边出现了一个局部最优点，右侧有一个全局最优点。当我们的梯度从右侧进行梯度下降时，就可能因为学习率低而无法跨越局部最优。导致模型陷入局部最优之中。这个不是深度学习要达到的目标。

鞍点

鞍点（Saddle point）在微分方程中，沿着某一方向是稳定的，另一条方向是不稳定的奇点，叫做鞍点。在泛函中，既不是极大值点也不是极小值点的临界点，叫做鞍点。

x = np.arange(-2.0, 2.0, 0.1)
fig, = d2l.plt.plot(x, x**3)
fig.axes.annotate('saddle point', xy=(0, -0.2), xytext=(-0.52, -5.0),
                  arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)');

简单的来说鞍点就是函数一阶导和二阶导都为0的点。导数为0了，梯度就不在下降了。
判断一个点是不是鞍点的一个条件是计算函数的Hessian矩阵的行列式，小于0就是鞍点。

给出一个3维空间鞍点的例子

x, y = np.mgrid[-1: 1: 31j, -1: 1: 31j]
z = x**2 - y**2

d2l.set_figsize((6, 4))
ax = d2l.plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 2, 'cstride': 2})
ax.plot([0], [0], [0], 'ro', markersize=10)
ticks = [-1,  0, 1]
d2l.plt.xticks(ticks)
d2l.plt.yticks(ticks)
ax.set_zticks(ticks)
d2l.plt.xlabel('x')
d2l.plt.ylabel('y');

梯度消失

x = np.arange(-2.0, 5.0, 0.01)
fig, = d2l.plt.plot(x, np.tanh(x))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)')
fig.axes.annotate('vanishing gradient', (4, 1), (2, 0.0) ,arrowprops=dict(arrowstyle='->'))

这里的梯度消失并不是真的消失，而是梯度值太小了，导致学习速率变得特别慢。

凸集

示例

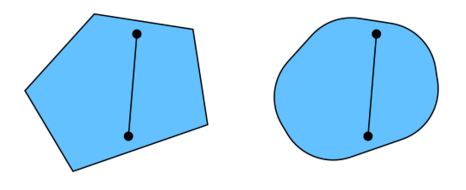
在一个凸集里，连接任意两点构成的直线上的点，依然在集合里面，这样的集合叫凸集。

常见凸集

超平面
$$w^{T}x=b$$
区域
$$w^{T}x\ge b$$
多面体
ps.凸集的交集也是凸集，凸集的和集不一定是凸集

凸函数（convex function）

凸优化的优化对象是凸函数。

定义

$$\lambda f(x)+(1-\lambda )f\left(x^{\prime }\right)\ge f\left(\lambda x+(1-\lambda )x^{\prime }\right)$$

图示

取图像上的两点连线，直线上任意一点的函数值都小于该点在直线上的函数值。


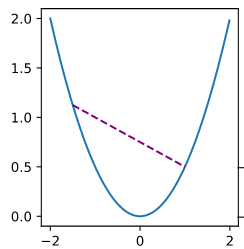
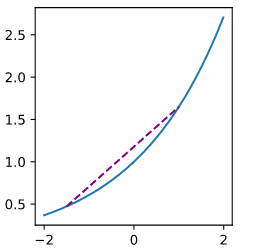
以上两个函数都是凸函数

def f(x):
    return 0.5 * x**2  # Convex

def g(x):
    return np.cos(np.pi * x)  # Nonconvex

def h(x):
    return np.exp(0.5 * x)  # Convex

x, segment = np.arange(-2, 2, 0.01), np.array([-1.5, 1])
d2l.use_svg_display()
_, axes = d2l.plt.subplots(1, 3, figsize=(9, 3))

for ax, func in zip(axes, [f, g, h]):
    ax.plot(x, func(x))
    ax.plot(segment, func(segment),'--', color="purple")
    # d2l.plt.plot([x, segment], [func(x), func(segment)], axes=ax)

Jensen 不等式

Jensen 不等式是上面凸函数公式的一个泛化形式
$$\sum _i{\alpha }_{i}f(x_i)\ge f(\sum _i{\alpha }_i{x}_i)$$
在概率论中，如果把${\alpha }_i$看成离散变量$x_i$的概率分布的值，那么上式可表达成
$$E(f(x))>f(E(x))$$
函数的期望大于期望的函数。

性质

1. 无局部极小值
2. 与凸集的关系
3. 二阶条件$$\ddot{f(x)}>0$$是凸函数的充要条件

常见凸函数

1. 数函数$e^{ax}$
2. 幂函数$x^a,x\in R正,1\le a||a\le 0$
3. 负对数函数 $-logx$
4. 负熵函数 $xlogx$
5. 范数函数 $||x|{|}_p$
6. $max(x_1,x_2,x_3...)$

凸优化问题的基本形式

求$$minimizef(x)$$
限制条件
$$subjectto:f_i(x)\le 0$$
$$h_j(x)=0,j=1,2,...p$$
其中$f_i(x)$为凸函数，$h_j(x)$为仿射函数

解法

拉格朗日乘子法
$$L(x,\alpha )=f(x)+\sum _i{\alpha }_i{f}_i(x)where{h}_j(x)=0$$
惩罚项
投影