sklearn机器学习:多项式朴素贝叶斯MultinomialNB
多项式朴素贝叶斯MultinomialNB多项式贝叶斯可能是除了高斯之外,最为人所知的贝叶斯算法了。它也是基于原始的贝叶斯理论,但假设概率分布是服从一个简单多项式分布。多项式分布来源于统计学中的多项式实验,这种实验可以具体解释为:实验包括n次重复试验,每项试验都有不同的可能结果。在任何给定的试验中,特定结果发生的概率是不变的。举个例子,比如,一个特征矩阵表示投掷硬币的结果,则得到正面的概率为P..
多项式朴素贝叶斯MultinomialNB
多项式贝叶斯可能是除了高斯之外,最为人所知的贝叶斯算法了。它也是基于原始的贝叶斯理论,但假设概率分布是服从一个简单多项式分布。多项式分布来源于统计学中的多项式实验,这种实验可以具体解释为:实验包括n次重复试验,每项试验都有不同的可能结果。在任何给定的试验中,特定结果发生的概率是不变的。
举个例子,比如,一个特征矩阵表示投掷硬币的结果,则得到正面的概率为P(X=正面|Y) = 0.5,反面的概率为P(X=反面|Y) = 0.5,只有这两种可能,并且两种结果互不干涉,两个随机事件的概率加和为1,这就是二项分布。这种情况下,适合于多项式朴素贝叶斯的特征矩阵应该长这样:

假设另一个特征X’表示投掷骰子的结果,则 i 就可以在[1,2,3,4,5,6]中取值,六种结果互不干涉,且只要样本量足够大,概率都为1/6,这就是一个多项分布。多项分布的特征矩阵应该长这样:

可以看出:
- 多项式分布擅长的是分类型变量,在其原理假设中,P(xi|Y)的概率是离散的,并且不同xi下的P(xi|Y)相互独立,互不不影响。虽然sklearn中的多项式分布也可以处理连续型变量,但现实中,
如果我们真的想要处理连续型变量,应当使用高斯朴素贝叶斯。 - 多项式实验中的实验结果都很具体,它所涉及的特征往往是次数,频率,计数,出现与否这样的概念,这些概念都是离散的正整数,因此,sklearn中的多项式朴素贝叶斯不接受负值的输入。
由于这样的特性,多项式朴素贝叶斯的特征矩阵经常是稀疏矩阵(不一定总是稀疏矩阵),并且它经常被用于文本分类。我们可以使用著名的TF-IDF向量技术,也可以使用常见并且简单的单词计数向量手段与贝叶斯配合使用。这两种手段都属于常见的文本特征提取的方法,可以很简单地通过sklearn来实现。
从数学的角度来看,在一种标签类别Y=c下,有一组分别对应特征的参数向量
θ
c
=
(
θ
c
1
,
θ
c
2
,
.
.
.
,
θ
c
n
,
)
\theta_c=(\theta_{c1},\theta_{c2},...,\theta_{cn},)
θc=(θc1,θc2,...,θcn,),其中n表示特征的总数。一个
θ
c
i
\theta_{ci}
θci表示这个标签类别下的第i个特征所对应的参数。这个参数被我们定义为:
θ c i = 特 征 X i 在 Y = 特 征 在 c 这 个 分 类 下 的 所 有 样 本 的 取 值 总 和 所 有 特 征 在 Y = 特 征 在 c 这 个 分 类 下 的 所 有 样 本 的 取 值 总 和 \theta_{ci}=\large\frac{特征{X_i}在Y=特征在c这个分类下的所有样本的取值总和}{所有特征在Y=特征在c这个分类下的所有样本的取值总和} θci=所有特征在Y=特征在c这个分类下的所有样本的取值总和特征Xi在Y=特征在c这个分类下的所有样本的取值总和
记作P(Xi|Y=c),表示当Y=c这个条件固定的时候,一组样本Xi在这个特征上的取值被取到的概率。
对于一个在标签类别下,结构为(m, n)的特征矩阵来说,我们有:
X
y
=
[
x
11
x
12
…
x
1
n
x
21
x
22
…
x
2
n
⋮
⋮
⋱
x
m
1
x
m
2
…
x
m
n
]
X_y =\left[ \begin{array}{c} x_{11} & x_{12} & \ldots & x_{1n} \\ x_{21} & x_{22} & \ldots & x_{2n} \\ \vdots & \vdots & \ddots\\ x_{m1} & x_{m2} & \ldots & x_{mn} \\ \end{array} \right]
Xy=⎣⎢⎢⎢⎡x11x21⋮xm1x12x22⋮xm2……⋱…x1nx2nxmn⎦⎥⎥⎥⎤
其中每个xji都是特征Xi发生的次数。基于这些,通过平滑后的最大似然估计来求解参数
θ
y
\theta_y
θy:
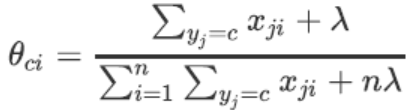
对于每个特征,
∑
y
j
=
c
x
j
i
\mathbf{\sum_{y_j=c}x_{ji}}
∑yj=cxji是特征Xi下所有标签为c的样本的特征取值之和,其实就是特征矩阵中每一列的和。
∑
i
=
1
n
∑
y
j
=
c
x
j
i
\mathbf{\sum_{i=1}^n\sum_{y_j=c}x_{ji}}
∑i=1n∑yj=cxji是所有标签类别为c的样本上,所有特征的取值之和,其实就是特征矩阵Xy中所有元素的和。
λ
\lambda
λ被称为平滑系数,令
λ
\lambda
λ>0来防止训练数据中出现过的一些词汇没有出现在测试集中导致的0概率,以避免让参数
θ
\theta
θ为0的情况。如果
λ
\lambda
λ=1,则这个平滑叫做拉普拉斯平滑,
λ
\lambda
λ<1,叫做利德斯通平滑。两种平滑都属于自然语言处理中比较常用的用来平滑分类数据的统计手段。
之前提到,系数
θ
c
i
\theta_{ci}
θci其实就是P(Xi|Y=c),这是对于每⼀一个特征而言,在Y=c取值下的概率。

且
P(Y=1|X)+P(Y=0|X)=1
但在最大后验估计中需要的是P(xi|Y=c),这是对于一个样本来说取到Y=c时的概率,那么,如何将一个特征上的概率变成一个样本在一个特征取值下的概率呢?其实很简单:
P(xi|Y=c)=
θ
c
i
x
i
\theta_{ci}x_i
θcixi
对于像掷骰子或者抛硬币这样的“是否发生”类型的实验而言,特征取值xi往往只有0和1两种选择,如果为0,则这个样本在这个特征下的概率取值就为0,如果为1,则这个样本在这个特征取值下的概率就为
θ
c
i
x
i
\theta_{ci}x_i
θcixi。
在sklearn中,用来执行多项式朴素贝叶斯的类MultinomialNB包含如下的参数和属性:
class sklearn.naive_bayes.MultinomialNB (alpha=1.0,fit_prior=True, class_prior=None)
其中:
alpha : 浮点数, 可不填 (默认为1.0)
拉普拉斯或利德斯通平滑的参数
λ
\lambda
λ,如果设置为0则表示完全没有平滑选项。但是需要注意的是,平滑相当于人为给概率加上一些噪音,因此
λ
\lambda
λ设置得越大,多项式朴素贝叶斯的精确性会越低(虽然影响不是非常大)。
fit_prior : 布尔值, 可不填 (默认为True)
是否学习先验概率P(Y=c)。如果设置为false,则所有的样本类别输出都有相同的类别先验概率。即认为每个标签类出现的概率是
1
n
_
c
l
a
s
s
e
s
\frac1{n\_classes}
n_classes1。
class_prior:形似数组的结构,结构为(n_classes, ),可不填(默认为None)
类的先验概率P(Y=c)。如果没有给出具体的先验概率则自动根据数据来进行计算。
布尔参数fit_prior表示是否要考虑先验概率,如果是False,则所有的样本类别输出都有相同的类别先验概率。否则,可以用第三个参数class_prior输入先验概率,或者不输入第三个参数class_prior让
MultinomialNB自己从训练集样本来计算先验概率,此时的先验概率为P(Y=Ck)=mk/m。其中m为训练集样本总数量,mk为输出为第k个类别的训练集样本数。总结如下:

通常,在实例化多项式朴素贝叶斯的时候,会让所有的参数保持默认。先来简单建一个多项式朴素贝叶斯的例子试试看:
#导⼊入需要的模块和库
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.metrics import brier_score_loss
#建立数据集
class_1 = 500
class_2 = 500 #两个类别分别设定500个样本
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [0.5, 0.5] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
,test_size=0.3
,random_state=420)
np.unique(Ytrain)
array([0, 1])
(Ytrain==1).sum()/Ytrain.shape[0]
0.49857142857142855
#归一化,确保输入多项式朴素贝叶斯的特征矩阵不带有负数
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
#建立一个多项式朴素贝叶斯分类器
mnb = MultinomialNB().fit(Xtrain_, Ytrain)
#重要属性:调⽤用根据数据获取的,每个标签类的对数先验概率log(P(Y))
#由于概率永远是在[0,1]之间,因此对数先验概率返回的永远是负值
mnb.class_log_prior_
array([-0.69029411, -0.69600841])
#可以使用np.exp来查看真正的概率值
np.exp(mnb.class_log_prior_)
array([0.50142857, 0.49857143])
#重要属性:返回一个固定标签类别下的每个特征的对数概率log(P(Xi|y))
mnb.feature_log_prob_
array([[-0.76164788, -0.62903951],
[-0.72500918, -0.6622691 ]])
'''重要属性:在fit时每个标签类别下包含的样本数。
当fit接口中的sample_weight被设置时,
该接口返回的值也会受到加权的影响'''
mnb.class_count_
array([351., 349.])
分类器的效果如何呢?用一些传统的接口试试:
mnb.predict(Xtest_)
array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0,
1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1,
...
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
mnb.predict_proba(Xtest_)
array([[0.49847128, 0.50152872],
[0.50065987, 0.49934013],
[0.50122363, 0.49877637],
...
[0.50156107, 0.49843893],
[0.50078711, 0.49921289],
[0.50197128, 0.49802872]])
mnb.score(Xtest_,Ytest)
0.5433333333333333
效果不太理想,思考一下多项式贝叶斯的性质,我们能够做点什么呢?来试试看把Xtiain转换成分类型数据吧:注意我们的Xtrain没有经过归一化,因为做哑变量之后自然所有的数据就不会有负数了
'''KBinsDiscretizer()是将连续型变量划分为分类变量的类,
能够将连续型变量排序后按顺序分箱后编码'''
from sklearn.preprocessing import KBinsDiscretizer
kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
Xtrain_ = kbs.transform(Xtrain)
Xtest_ = kbs.transform(Xtest)
mnb = MultinomialNB().fit(Xtrain_, Ytrain)
mnb.score(Xtest_,Ytest)
0.9966666666666667
可以看出,多项式朴素贝叶斯的基本操作和代码都非常简单。同样的数据,如果采用哑变量方式的分箱处理,多项式贝叶斯的效果会突飞猛进。
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容








所有评论(0)