嵌入式系统的序列化

借鉴bitcoin RPC API手册、bitcoincore及bitcoin zkcp版本1、listtransactionsThe listtransactions RPC returns the most recent transactions that affect the wallet.listtransactions调用返回最近发生的与钱包有关的交易清单。该调用需要节点 启用钱包...

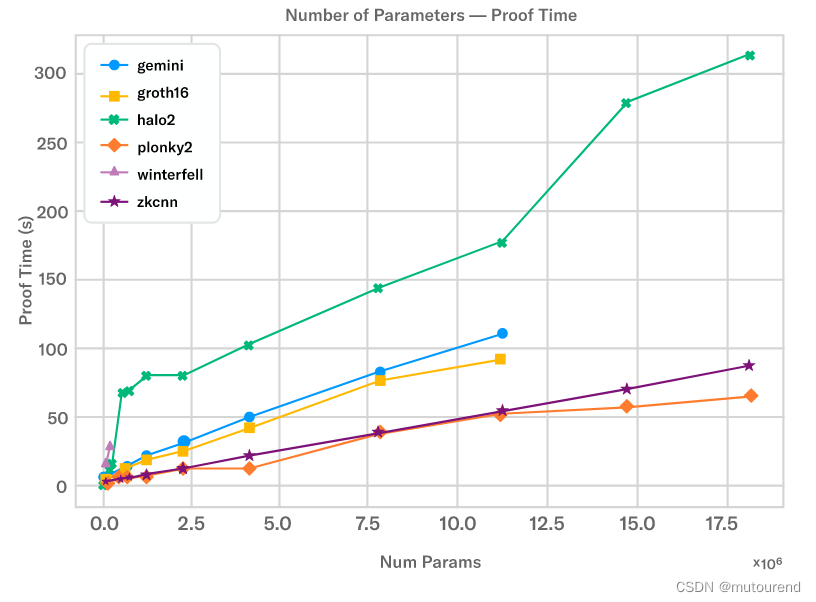
zkML零知识机器学习介绍

区块链商业模式

DeFi领域融资情况有：1）：融资530万美金。由North Island Ventures, Chapter One, Node Capital领投，投资者有Arrington Capital, Maelstrom, Version One Ventures, Purpose Investments。为以太坊网络的liquid staking协议，不同于其他协议，允许ETHstakers完全控制

主流区块链共识算法大全

1. 区块链账户模型2. 支持隐私保护的UTXO模型区块链系统参考资料：[1] 2019年论文《BlockMaze: An Efficient Privacy-Preserving Account-Model Blockchain Based on zk-SNARKs 》...

1. 引言比特币和以太坊采用Secp256k1，NEO使用secp256r1，波卡、Cardano、NEAR 和 Solana 等使用Ed25519。详细可参看：Cryptography behind top 20 cryptocurrenciesNameTypeSigning algCurveHashAddress encod

区块链扩容：水平扩展 vs.垂直扩展

ZKML：区块链世界的AI+隐私