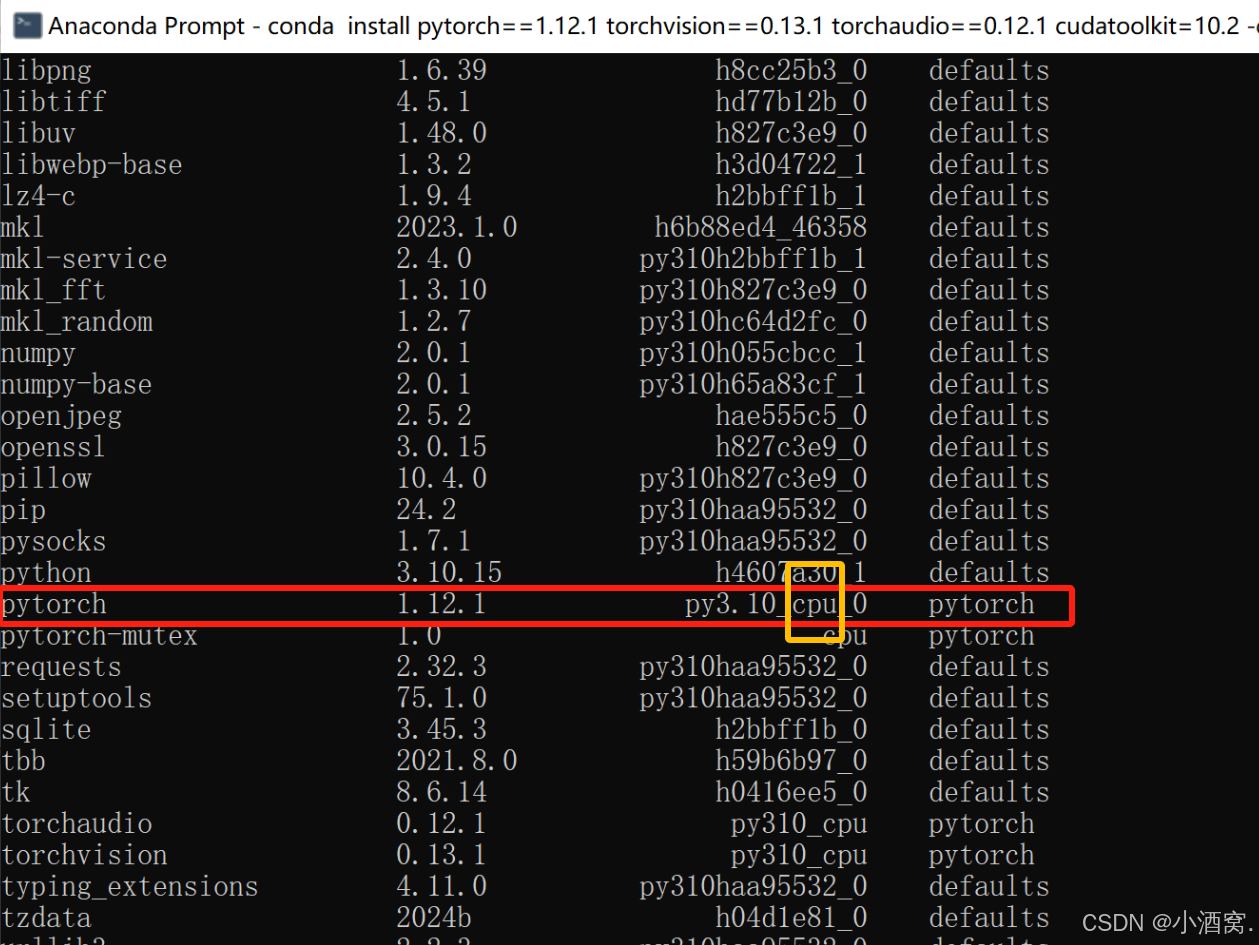
完美解决 torch.cuda.is_available() 仍返回 False，因为你的 pytorch 被迫下载成了 cpu 版本。

快速入门 git，配合使用 vscode 方便可视化操作，快速上手，半天学会 git 基础操作！

完美解决 torch.cuda.is_available() 仍返回 False，因为你的 pytorch 被迫下载成了 cpu 版本。

题意把 6 支队伍分成两组，把所有的可能方案按照下面的筛选方式找到最佳方案：思路比较简洁的一个方法是，将每一条方案中的元素都存储到结构体中，然后在结构体中重载运算符，根据给出的筛选策略将所有方案排序，排过序之后的首条方案便是最佳方案。怎么按照筛选策略排序呢？对于一条筛选，在结构体中申请元素表示该筛选条件满不满足，如果满足置为1，否则为0。在重载小于号时，按照该元素从大到小排序。这样满足该条件的就放

7-1 懂的都懂 (20 分)题意：给出n个数a1,a2,a3…an。给出m个数，判断这个数是否为 从n个数中抽4个，这4个数的平均数？思路：

Linking题意：从 nnn 个数中挑选若干数。条件：对于每个位置 iii，该位置和下一位置至少有一个被选。问，挑选的数的 平均数 和 中位数 最大分别为多少？ (中位数：除2上取整）思路：发现如果一个数列满足其平均数不小于 mid，那么 mid 就可以往右走，继续判断，直到不满足了，那么这个 mid 就是能够满足的最大平均数。于是就可以用 二分答案。中位数同理。碰见平均数和中位数就想转化平均数

一、01背包题目描述：有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的体积是 vi，价值是 wi 。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。每件物品只能 不选0，或者选一次1，所以叫做01背包。（好生动 QwQ）—————朴素做法：1、状态表示：f[i][j]表示从前i个物品中选，总体积不超过j的最大价值；2、属性： 最

前言：今天碰见了这个操作，发现在状态压缩的时候特别好用，就整理一下吧。bitset 就相当于一个 只能存储二进制，也就是 0 和 1 的 bool 数组但是可以直接当作一个数进行左移右移，取或取反等二进制操作。如果直接用 bool 数组存储二进制每一位的话，n 位存储复杂度为 O(n)，但是用 bitset 的话复杂度会减少到 O(n/32)。所以一般用二进制状态压缩时就会用 bitset。一、定

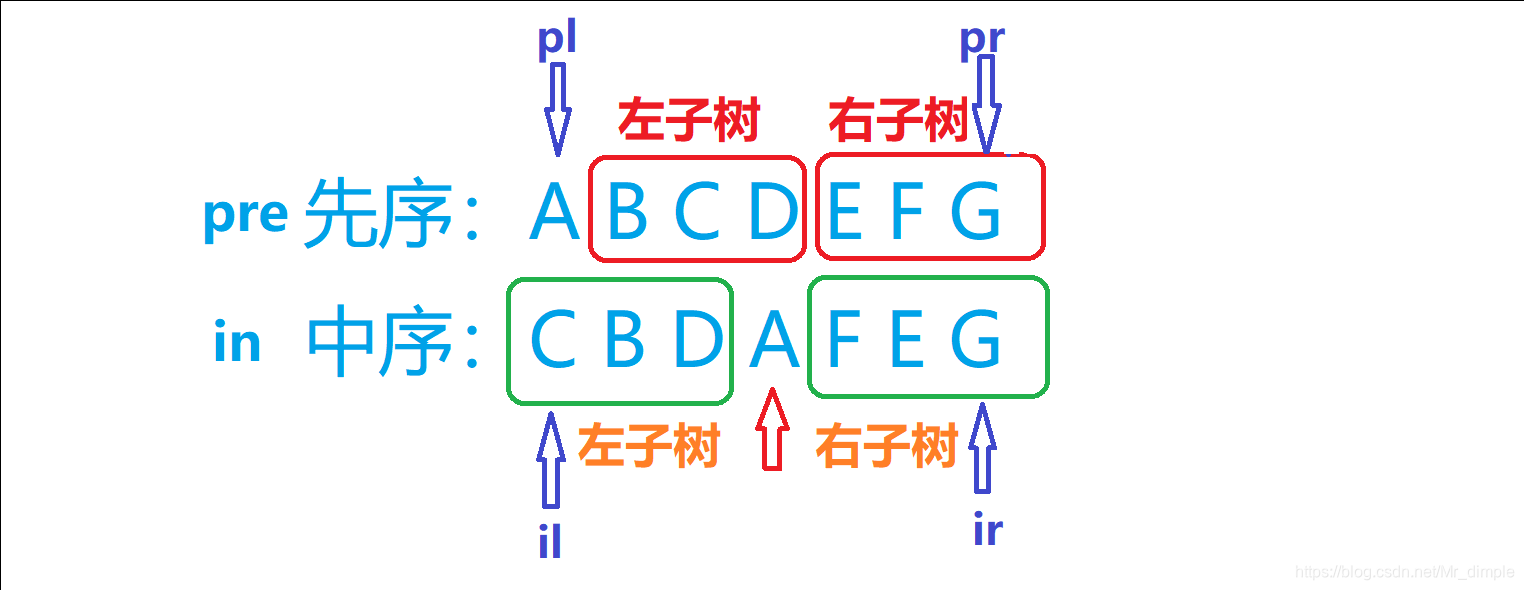
先中和后中的思路相同，这里先以先中举例：思路：通过递归，不断压缩中序和先序序列的长度，从而确定左右子树。根据先序排列的性质，第一个数则是这个序列中所有点的根节点root。确定通过map数组确定该点在中序序列中的位置k。...

很多人对二分很困惑，可能二分的边界很难掌握，也许是判断条件难写...很幸运，你找到了这篇文章，仔细看下去，这篇文章将带你**学透二分**！！！