
简介
该用户还未填写简介
擅长的技术栈
可提供的服务
暂无可提供的服务
本文探讨了在鸿蒙分布式系统中如何运用离散数学中的二元关系和等价类概念解决数据一致性问题。文章首先介绍了二元关系的自反性、对称性和传递性三大特性及其业务对应场景,然后阐述了等价关系和商集的数学本质及其在数据去重和分组中的应用。通过系统架构设计、Flutter核心代码实现和实战案例,展示了如何基于等价类合并算法处理分布式数据冲突。文章强调数学思维在保证数据一致性、稳定性和严密性方面的重要作用,为开发分

本文探讨了数论在鸿蒙应用开发中的实际应用,重点分析了哈希函数背后的数学原理。通过同余理论和素数分布特性,文章揭示了哈希表设计中选择素数的科学依据,并展示了Flutter中基于31-Hash算法的Key生成实现。作者还设计了哈希碰撞模拟器和文件完整性校验系统,验证了数论在构建高效、安全标识系统中的关键作用。文章指出数论为数据管理提供了数学基础,能实现纳秒级唯一性判定和可靠的安全校验。

本文深入探讨了贝塞尔曲线在HarmonyOS NEXT UI设计中的应用。通过解析二阶和三阶贝塞尔曲线的数学原理与实现方法,展示了如何利用Flutter的Path类创建流体视觉效果。文章包含核心代码示例、参数对照表和实战案例,如波浪背景裁剪和液态刷新球动画,揭示了贝塞尔曲线在实现鸿蒙系统"自然流体"风格中的关键作用。从几何原理到代码实现,本文为开发者提供了将数学优雅转化为视觉美

摘要:柏林噪声场在鸿蒙系统中的艺术应用 本文探索了柏林噪声算法在数字艺术中的应用,重点研究了如何通过伪随机演化模拟自然界的混沌美学。文章提出了一种基于多重三角函数叠加的数学模型,实现音频驱动的动态噪声场效果。通过非线性映射和频域叠加,构建了具备呼吸感的极光视觉形态。在鸿蒙系统实现上,采用步长优化、分层渲染等技术解决性能瓶颈,最终呈现出随音乐律动变化的极光幻彩效果。本文为混沌美学在UI设计中的应用提
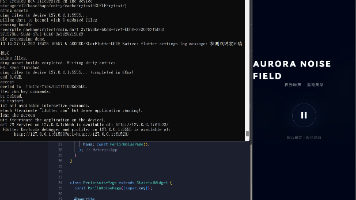
本文介绍了在鸿蒙系统上实现基于物理仿真的粒子动效设计。通过万有引力和斥力模型构建动态粒子物理场,利用欧拉积分更新粒子状态,创造出星云爆发般的视觉效果。文章详细阐述了数学模型、逻辑流程和核心代码实现,重点优化了鸿蒙系统下大规模粒子渲染的性能问题,包括批量绘制、物理逻辑简化和渲染树卸载等技术。这种将物理规律与艺术表达相结合的设计方案,为用户带来震撼的视觉体验,展现了技术实现与美学表达的完美融合。

本文探讨了OpenHarmony跨平台开发中的性能优化问题,重点介绍了离散数学中的计算复杂度理论及其应用。文章分析了Big O符号在量化算法性能中的作用,阐述了鸿蒙低功耗模式下的复杂度约束标准,并提供了系统架构设计方案和Flutter代码实现。通过对比线性搜索和二分搜索的复杂度差异,展示了如何在高性能列表渲染中应用这些理论。最后总结了离散数学在鸿蒙开发中的核心价值,强调其作为构建高效应用的底层逻辑

本文介绍了在OpenHarmony系统上实现丝绸流体视觉效果的算法设计。通过三阶贝塞尔曲线模拟丝绸飘动形态,结合音频能量动态调整曲线张力,创造出富有呼吸感的视觉动效。文章详细解析了数学模型构建、音频驱动逻辑和核心绘制算法,包括贝塞尔曲线控制点计算和性能优化策略。这种技术将刚性频谱转化为柔性流动的视觉效果,实现了从机械精准到有机律动的美学跨越,为后续研究柏林噪声场等更复杂的视觉模拟奠定了基础。

在浩瀚的宇宙尺度下,地球生命从冥古宙的炼狱到现代文明的繁荣,跨越了逾 38 亿年的壮丽征程。物种的进化与变迁,本质上是一场关于基因信息在时间洪流中不断自我重构与环境博弈的宏大史诗。本文旨在探讨如何利用 Flutter 这一高性能跨平台框架,结合鸿蒙系统(HarmonyOS)的全场景协同能力,构建一款名为“EVO-CHRONOS (进化纪元)”的沉浸式生命科学应用。我们将深度解析系统的时空维度建模逻
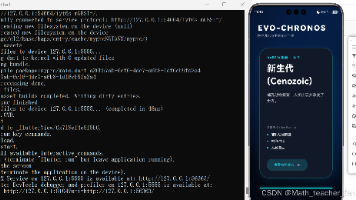
在浩瀚的宇宙尺度下,地球生命从冥古宙的炼狱到现代文明的繁荣,跨越了逾 38 亿年的壮丽征程。物种的进化与变迁,本质上是一场关于基因信息在时间洪流中不断自我重构与环境博弈的宏大史诗。本文旨在探讨如何利用 Flutter 这一高性能跨平台框架,结合鸿蒙系统(HarmonyOS)的全场景协同能力,构建一款名为“EVO-CHRONOS (进化纪元)”的沉浸式生命科学应用。我们将深度解析系统的时空维度建模逻

在浩瀚的宇宙尺度下,地球生命从冥古宙的炼狱到现代文明的繁荣,跨越了逾 38 亿年的壮丽征程。物种的进化与变迁,本质上是一场关于基因信息在时间洪流中不断自我重构与环境博弈的宏大史诗。本文旨在探讨如何利用 Flutter 这一高性能跨平台框架,结合鸿蒙系统(HarmonyOS)的全场景协同能力,构建一款名为“EVO-CHRONOS (进化纪元)”的沉浸式生命科学应用。我们将深度解析系统的时空维度建模逻











