搜索：在一个状态空间里，从起始状态开始，通过一系列合法动作找到目标状态的过程。

许多 AI 中的问题都可以理解为“搜索问题”

• 下棋：在棋局空间搜索最佳落子

• 路径规划：在地图空间搜索最短路

• 机器学习中的分类问题：在函数空间搜索最优分类器（函数）

• 运筹学中的函数最小化/最大化问题：在参数空间里找最小点/最大点（单纯形法 顶点的移动）

• 深度学习：在参数空间搜索神经网络的最优权重

区别在于：空间的结构不同 搜索方法不同

1. 状态空间图

Ex.1 两个房间吸尘器

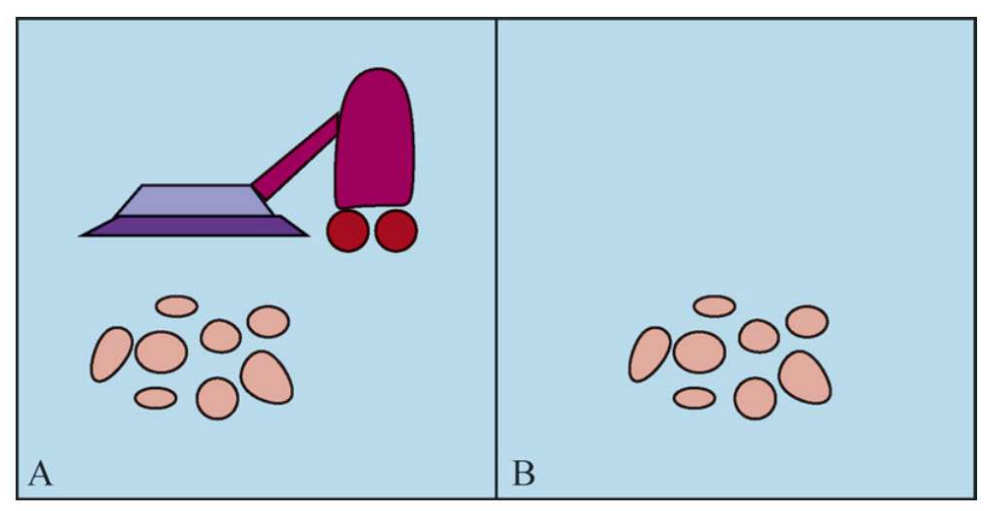
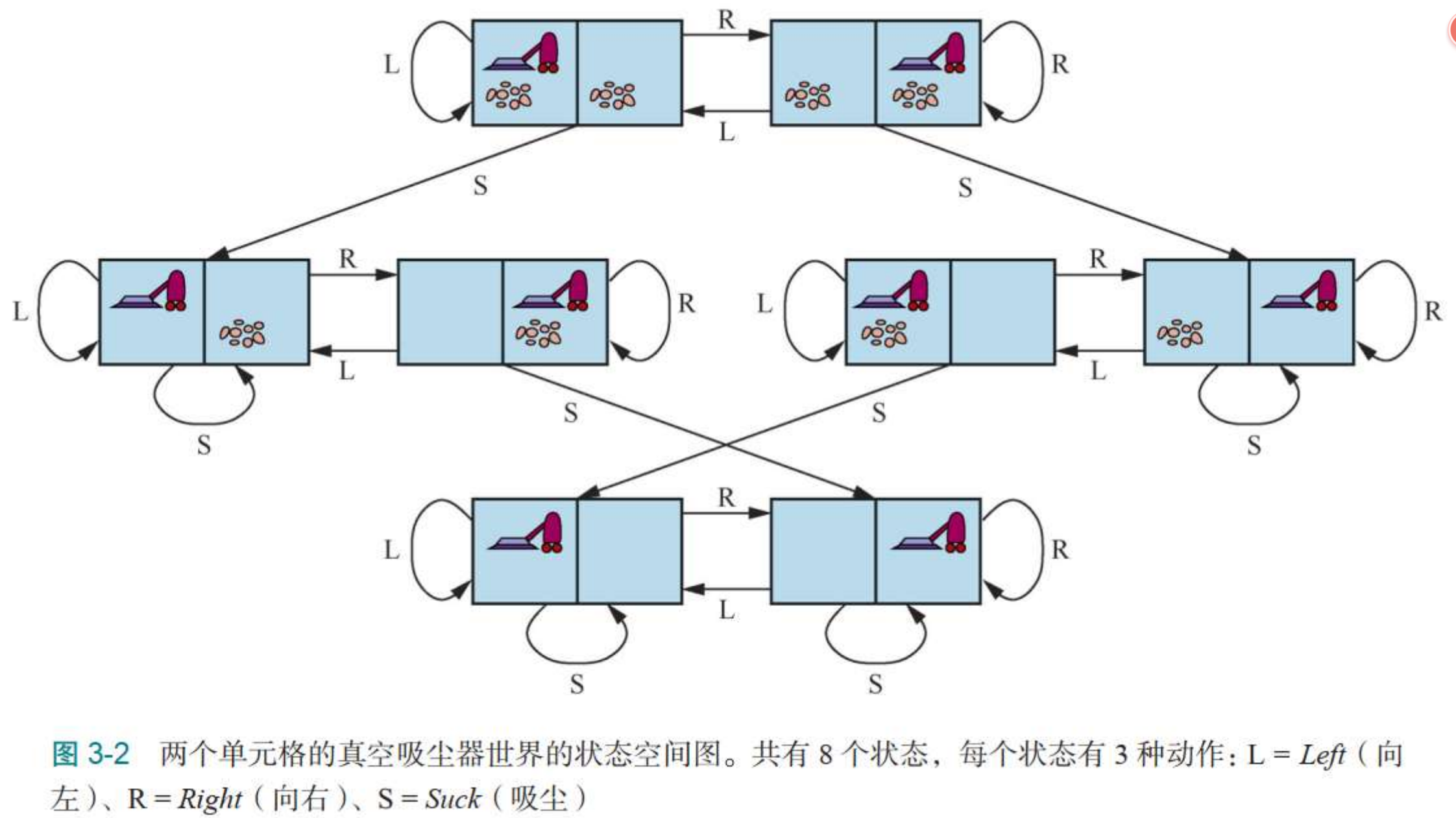
一个只有两个方格的真空吸尘器世界。每个位置可以是干净的，也可以是脏的，智能体可以向左移动L 或向右移动R，可以清理S 它所占据的方格。不同版本的真空吸尘器世界允许不同的规则，例如智能体可以感知什么，它的动作是否总是成功等.

状态三元组(Cleaner,A,B)表示：吸尘器现在在A还是B / A是否干净 Yes or No / B是否干净；

1. 状态空间 |S| 8个元素； n个房子就 n*2^n；    2. 初始状态为S中任意情况

3. 目标状态 房间都干净（全为Yes）吸尘器任意房间

4. 动作集合有(Left, Right, Suck) 往左移动 往右移动 和清洁

5. 状态转移 比如  清洗把A变干净 T((A,N,N),Suck) = (A,Y,N)    右移到B: T((A,Y,N),Right) = (B,Y,N)

6. 动作代价函数Cost  行动的消耗 比如 C((A,N,N),Suck) 吸尘A房间的消耗资源之类

Ex.2 迷宫

1. 状态空间：在地图上的各个位置

2. 初始状态：迷宫入口位置

3. 目标状态：迷宫出口位置

4. 动作集合：按规则移动 比如上下左右之类

5. 状态转移：状态+动作 之后的位置

6. 动作代价函数Cost：移动损耗；比如我目标是最小化步数 移动一次就损耗1步

2. 搜索算法

https://clementmihailescu.github.io/Pathfinding-Visualizer/#  可视化迷宫搜索

设置起始点 目标点 地图障碍；选择搜索算法 可视化进行搜索过程。

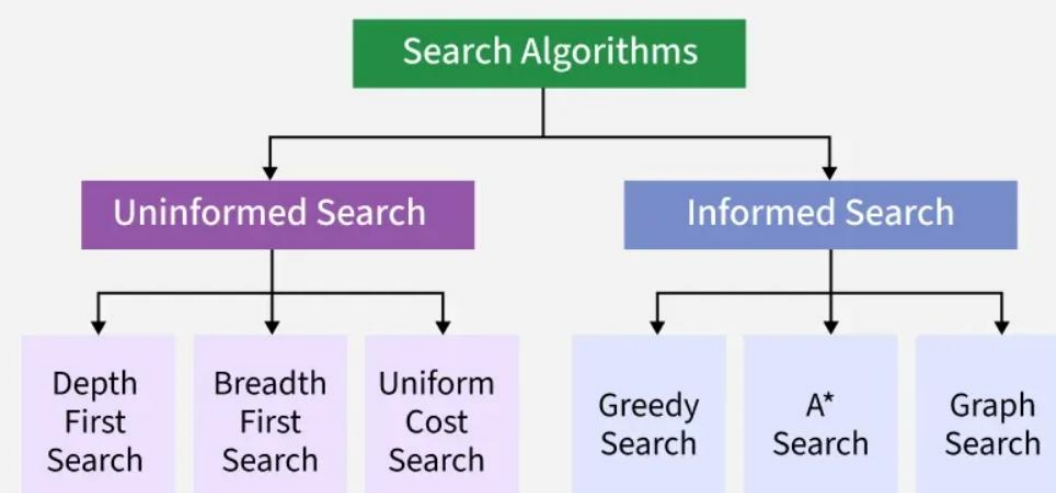
无信息搜索/盲目搜索（Uninformed Search）

• 智能体对状态空间与目标状态的关系不知情

• 穷举搜索（Brute force） • BFS, DFS, UCS 

有信息搜索/知情搜索（Informed Search）

• 使用与目标状态有关的特定领域信息       • Greedy, A*

2.1 宽度/广度优先搜索（Breadth-First Search, BFS）

先扩展根节点，然后1. 扩展根节点的所有后继节点

2. 检查是否为目标节点，3. 再扩展后继节点的后继并检查，以此类推。

Ex.1 迷宫问题

先将图转换为 图论形式（顶点和边表示）

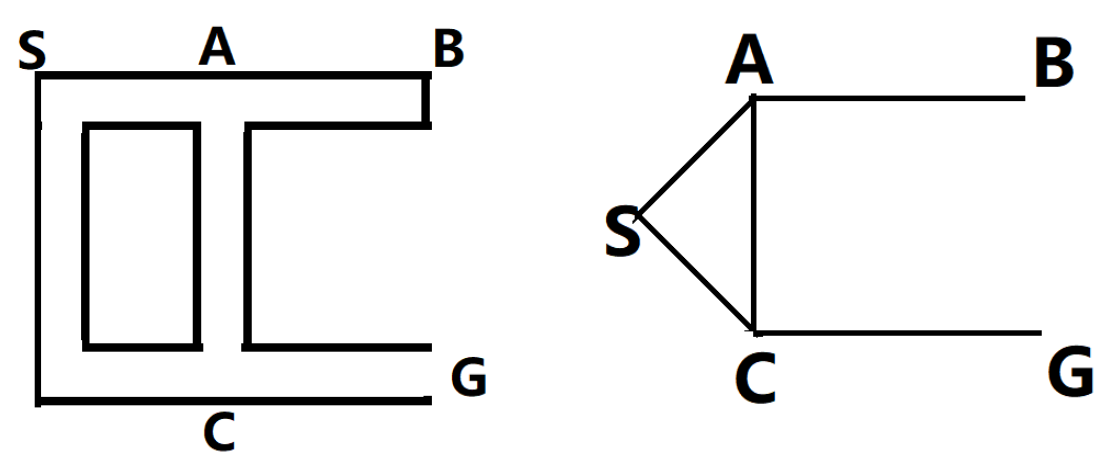
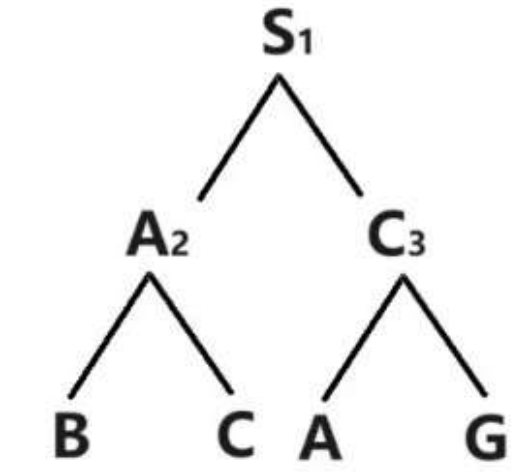
每次站在一个节点 做所有动作 看能转换到哪些状态

Ex.2 数字华容道

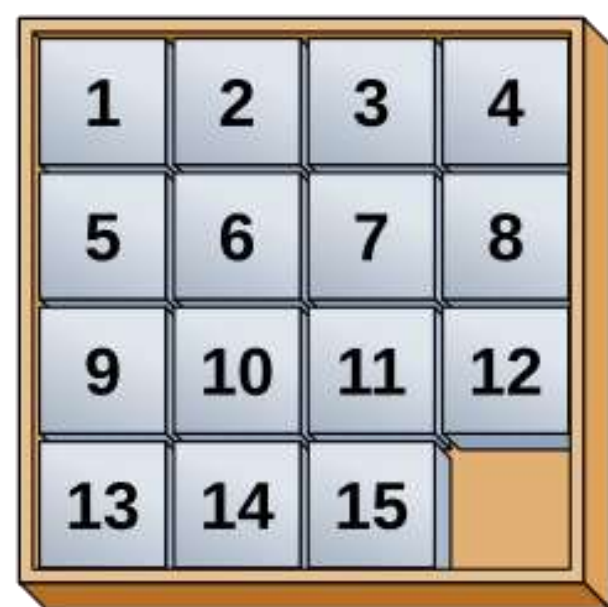
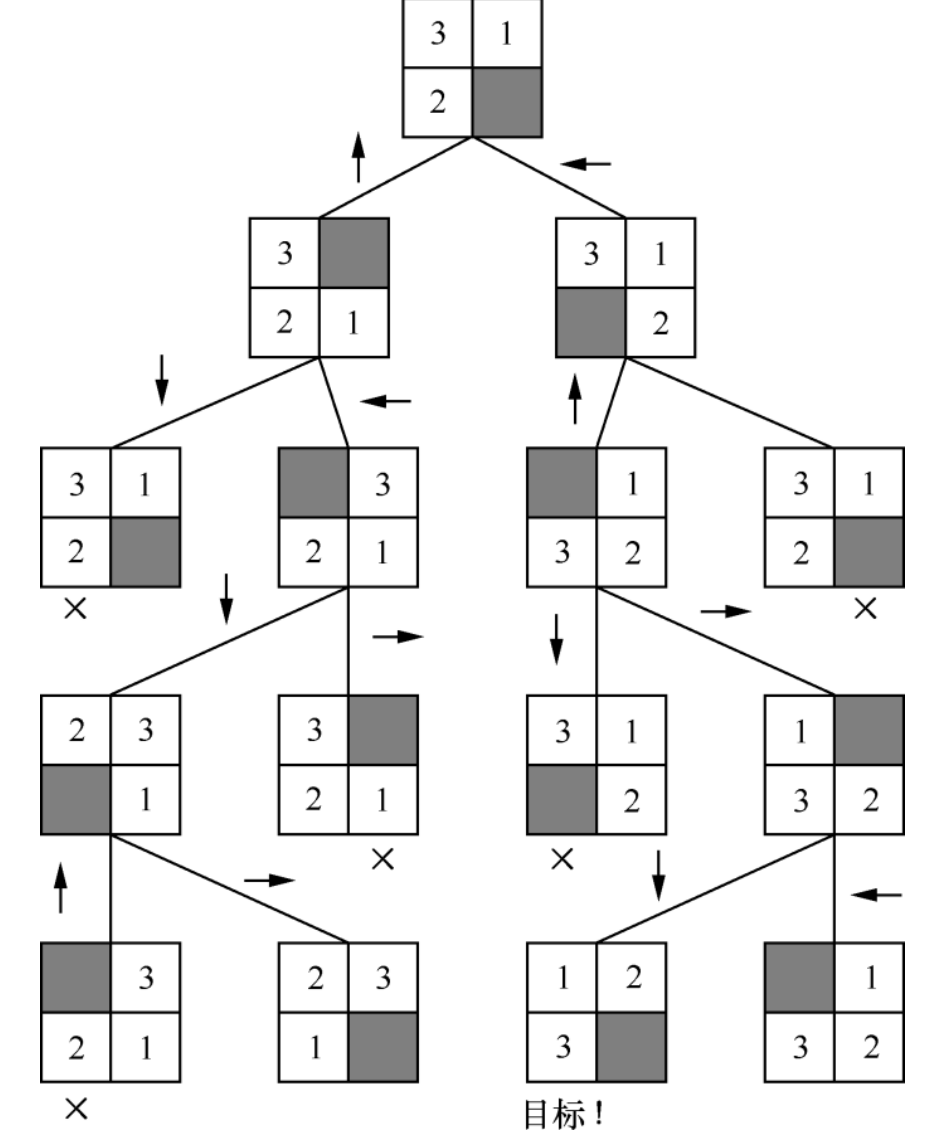
动作空间 围绕中间的空 和上下左右位置交换：比如上面 左 <- 就代表把15移动到空格上

把矩阵展平成向量 T( (312* ), 上) = (3*21)

搜索树中 与之前状态重复则剪枝

n个格子状态空间总数：n! / 2。  因为无论怎么移动 展开序列的逆序数奇偶性不变

比如 3*3 九个格子 八数码问题 则有 9! / 2 个状态。

比如这个四阶的 做上下调换 3->0 逆序数奇偶变，（逆序数+“*”所在行）奇偶不变

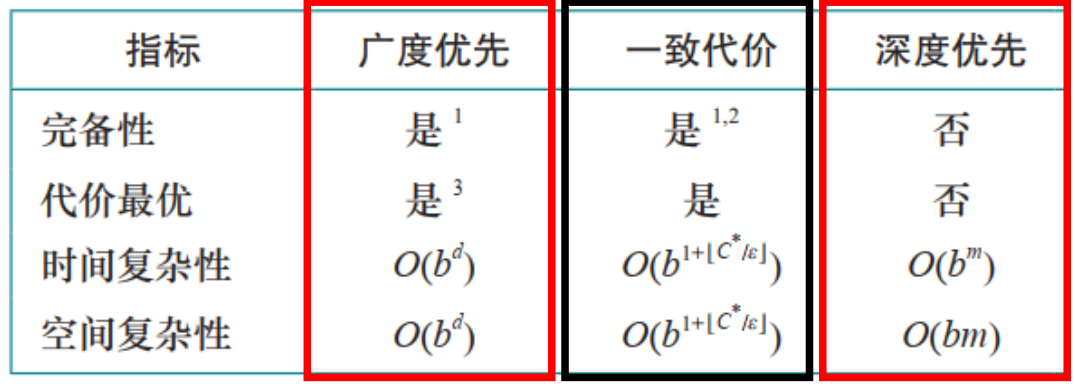
• 完备性：有限分支的情况下，BFS是完备的

• 最优性：BFS总能找到一个动作数量最少的解（步数更少的解都被pass了）

                 如果所有动作的代价相同，则BFS代价最优

因为前面d项等比数列 b≥2 时 小于b^d； 所以求和小于 2*b^d  即O(b^d)

2.2 深度优先搜索（Depth-First Search, DFS）

• 总是优先扩展边界中最深的节点

• 搜索先直接到达搜索树的最深层，这里的节点不存在后继节点

• 然后，搜索将回退到下一个仍存在未扩展后继节点的最深的节点。

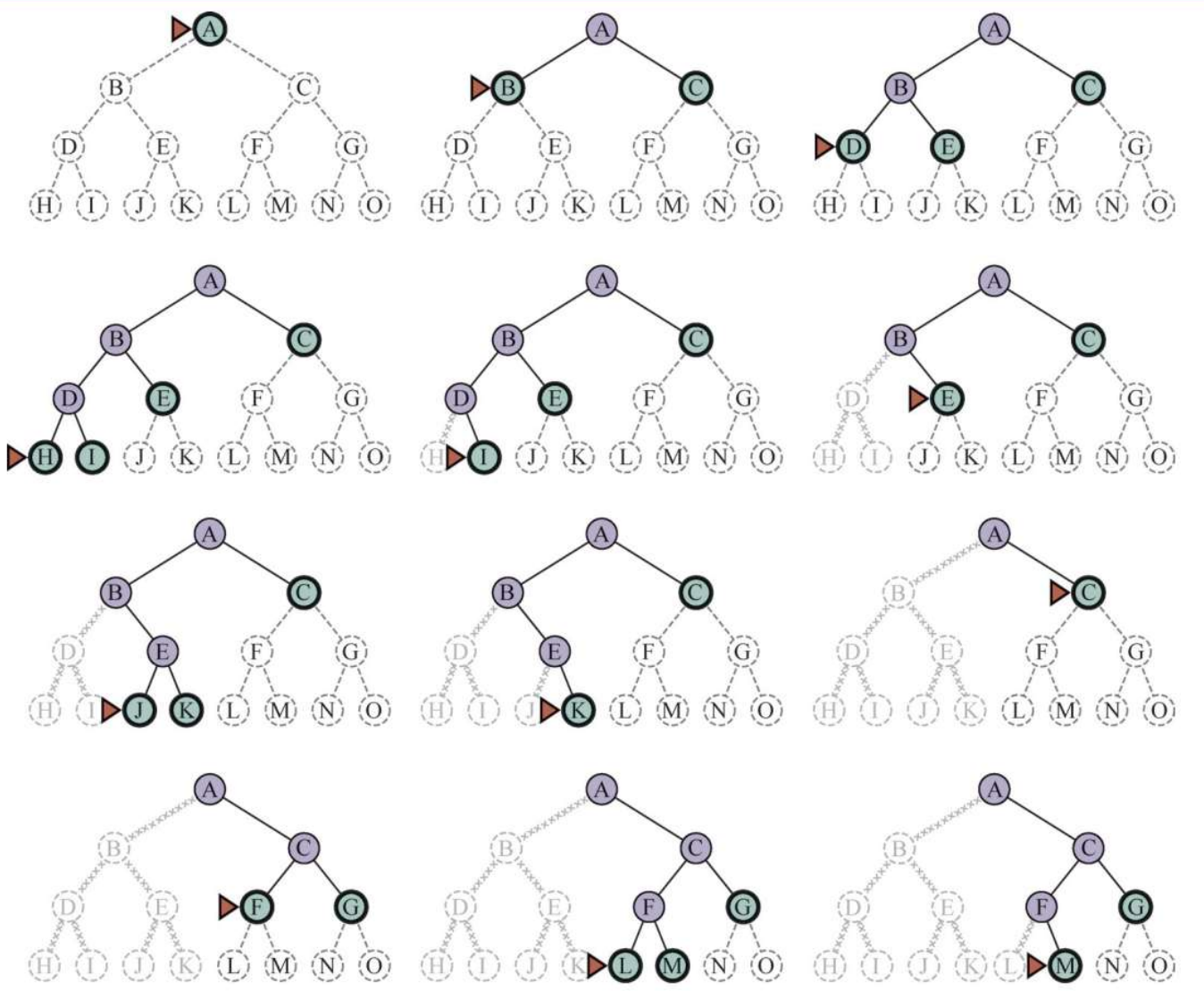
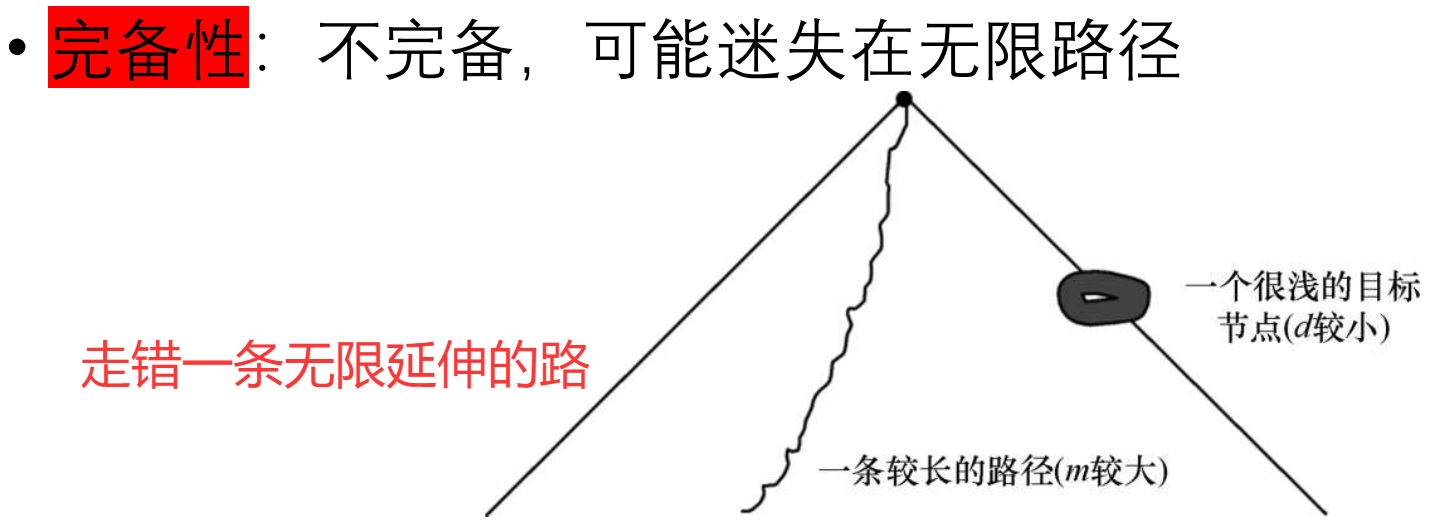
DFS优势 O(bm)的空间复杂度 ； 解比较深的dfs 比较浅的bfs

指数复杂度的问题，在未来计算机运算速度提升很多之后 解决问题规模的提升不显著

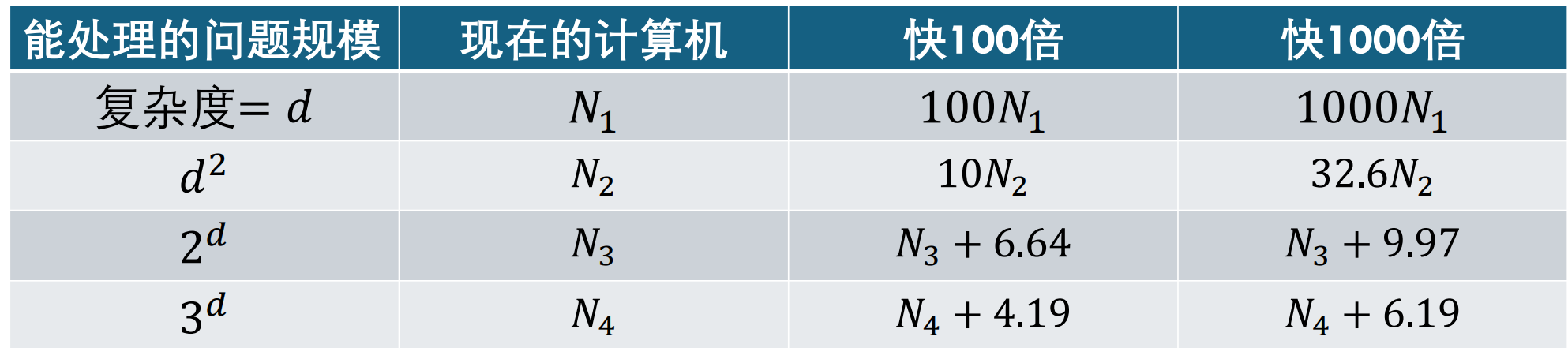
2.3 一致代价搜索（Uniform Cost Search, UCS）

类似Dijkstra思想，每次扩展 用距离起点最近 / 代价最小的点扩展

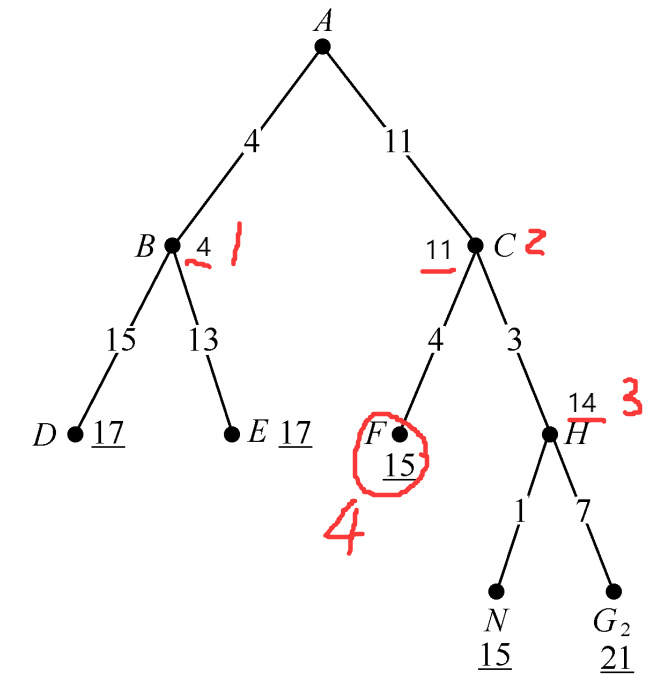
初始 A扩展出了B C；B代价最小扩展出D E；

C D E 中 C代价最小；扩展出 F H;            D E F H 中 H代价最小 扩展出 N G;

D E F N G中 F代价最小，准备扩展 F。

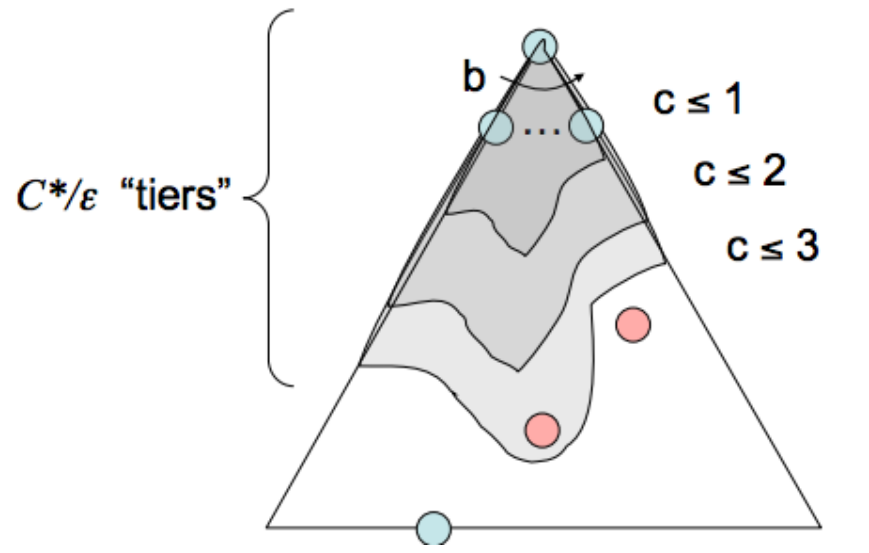
假设所有动作代价都是正数 达到的解则是代价最优的。

2.4 无信息与有信息 Informed Search

BFS/DFS/UCS: 最坏情况下均为指数级复杂度

盲目搜索：直到看到Goal才停止，途中对于Goal没有任何信息

贪心算法（Greedy Best-First Search）

每次扩展Heuristic (ℎ(n)) 最小的点，即（可能）最接近Goal的点

A* Search 结合UCS & Greedy

A*的启发式函数h

可容许Admissibility

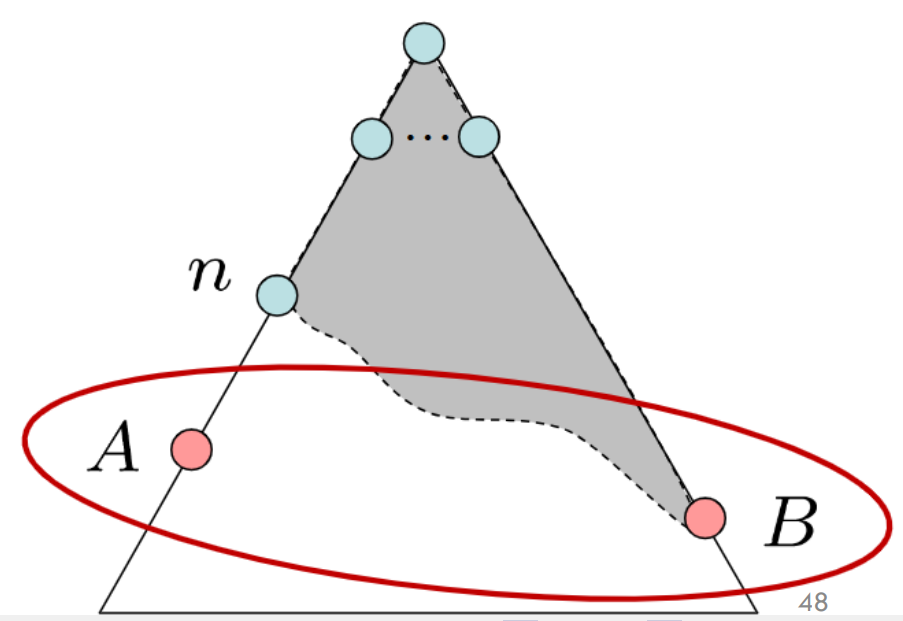
证明：设 A、B均为目标点 h(A) = h(B)=0 ；A是最优点 g(A)=c*<g(B)

因为 f = h + g 所以 f(A)<f(B) 所以保证搜索到 B之前就搜索到A了。

h(n) ≤ h*(n)   g(n)+h*(n)=f(A)

f(n) = g(n) + h(n) ≤ f(A) 即

一致性Consistency

一致性的A*下，一个节点第一次被扩展时，它的 g 就是最优路径代价。每个点只被扩展一次。

   

Dominance占优性

如8数码问题 使用h1(错位滑块数) h2(曼哈顿距离)

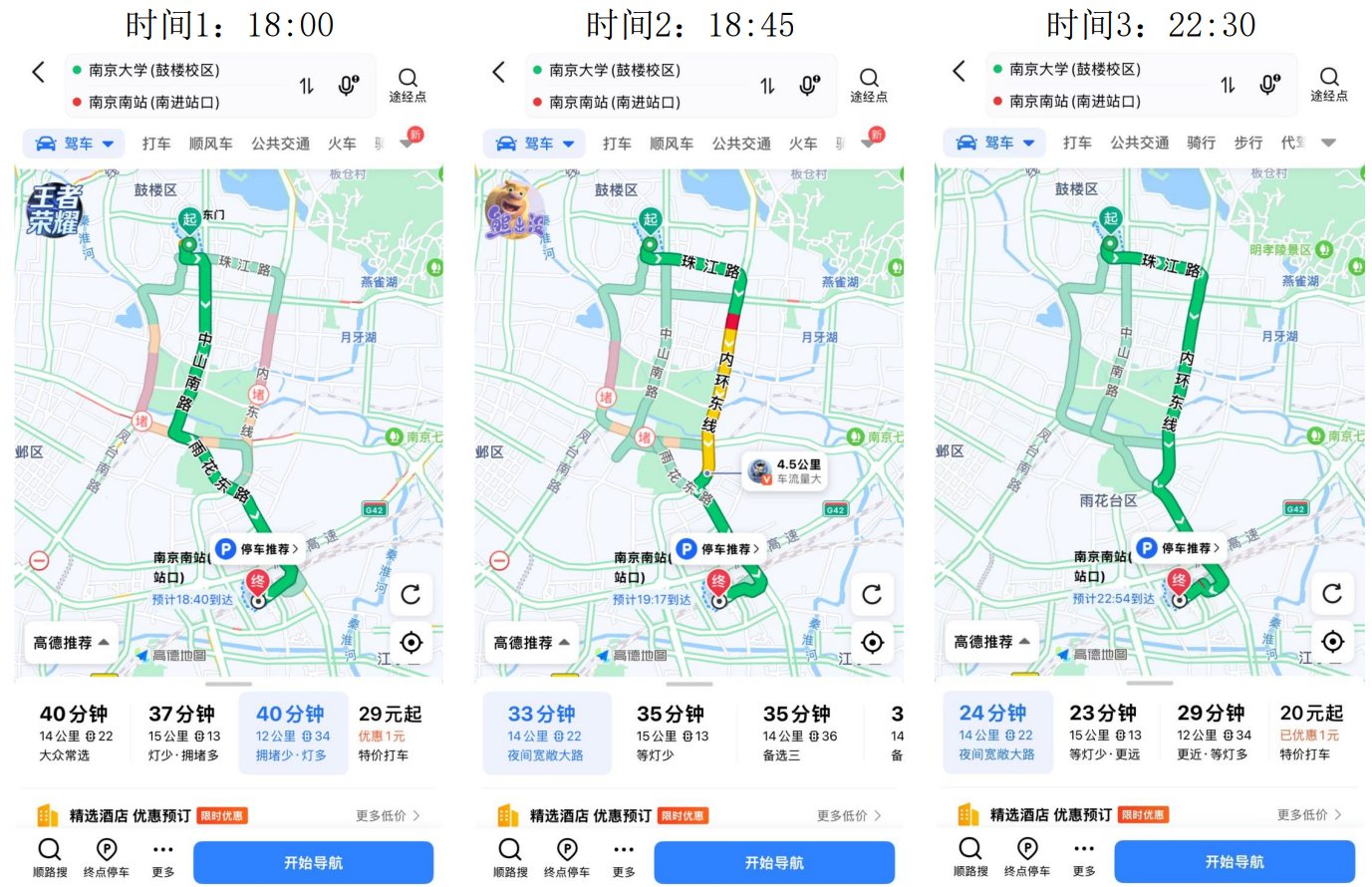
搜索应用到实际还需要进行 条件的完善和修正，如高德地图 在同一地点、不同时间段，车流量不同得到的路线规划与预期时间不同。