[旧]Markov Decision Processes: A Tool for Sequential Decision Making under Uncertainty
摘要:本文介绍了马尔可夫决策过程(MDP)在医疗决策中的应用,通过比较MDP与传统决策分析方法在活体肝移植最佳时机问题上的表现。研究表明,MDP不仅能更高效地求解最优策略(计算时间显著少于传统方法),还能处理序列决策中的不确定性。文章阐述了MDP的核心概念、求解方法(后向归纳法、价值迭代和策略迭代)及其在医疗领域的潜力,强调其在处理复杂临床决策问题时的优势。案例显示MDP与传统方法得出的最优移植策
Markov Decision Processes: A Tool for Sequential Decision Making under Uncertainty
摘要
我们提供了一个关于马尔可夫决策过程(MDP)构建和评估的教程,这些强大的分析工具在许多工业和制造应用中被广泛使用,但在医学决策制定(MDM)中却未得到充分利用。我们展示了如何利用MDP解决不确定性的顺序临床治疗问题。马尔可夫决策过程扩展了标准的马尔可夫模型,因为决策过程嵌入到模型中,并且随着时间的推移做出多次决策。此外,他们比标准决策分析具有显著优势。我们通过使用这两种方法解决最佳移植时机问题来比较MDPs和基于马尔可夫的模拟模型。两种模型都产生了相同的最优移植政策和相同患者的预期寿命。
求解MDP模型的时间明显少于求解马尔可夫模型的时间。我们简要描述了应用于医学决策的MDPs文献的增长情况。
序贯决策 (Sequential Decision Making)
不确定性 (Uncertainty)
动态规划 (Dynamic Programming)
最优策略 (Optimal Policy)
医疗决策 (Medical Decision Making, MDM)
一、绪论
1.1 传统决策分析的局限性

标准马尔科夫模型对一种决策组合进行评估,如果决策组合有几百万站,计算量则非常大。遇到了挑战!
1.2 MDP:更强大的决策工具

1.3 MDP 的定义:离散时间 MDP

1.4 MDP 的核心概念:决策规则与策略
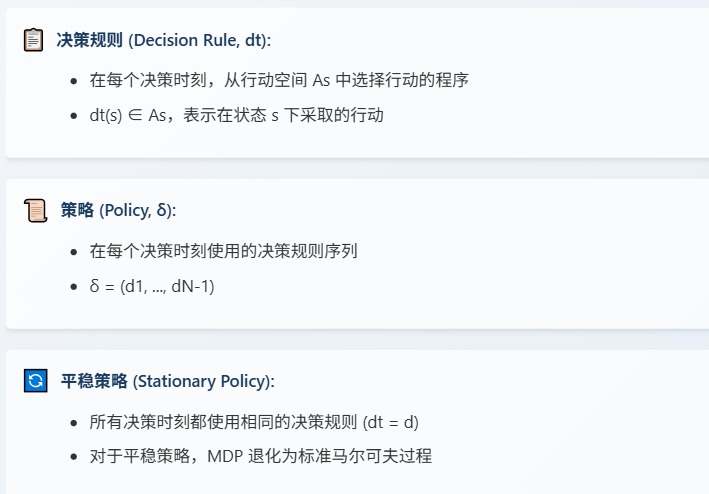
决策规则就像医生每天的查房决定:比如当病人MELD评分=20时选择"等待",MELD=30时选择"移植"。这相当于在每个状态下的具体行动指南. 一状态一决策。
策略则是整个治疗过程的完整方案:比如"在MELD<30时都选择等待,MELD≥30时立即移植"。这相当于把各个决策规则串联起来形成完整的治疗方案。 所有状态的决策。
1.5 MDP 的目标:最大化长期期望奖励

第二公式Ut∗U^*_tUt∗中,对于当前的状态sts_tst我们应该采取哪个动作a∈Ata \in A_ta∈At才能获得总的期望的奖励最大化。
pt(j∣st,a):=pt(st+1∣st,a)p_t(j|s_t,a) := p_t(s_{t+1}|s_t,a)pt(j∣st,a):=pt(st+1∣st,a) 下一个状态的转移概率。
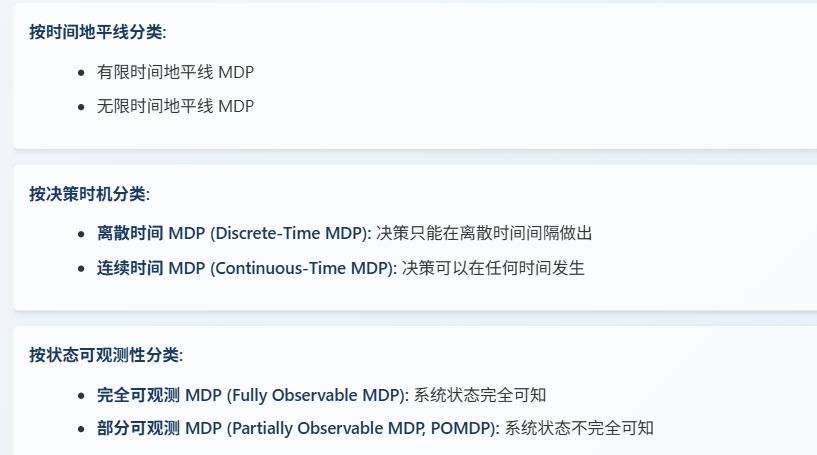
1.6 、MDP的分类

在无限时间MDP中,我们通常会引入一个折现因子,来保证未来奖励的总和是有限的,从而确保最优策略的存在。
当然,无限时间MDP也有一些假设条件,比如奖励和转移概率是平稳的,也就是不随时间变化,同时我们还需要一个折现因子,以及状态和行动空间最好是离散的。
1.7 MDP 的类型:离散时间、连续时间、POMDP
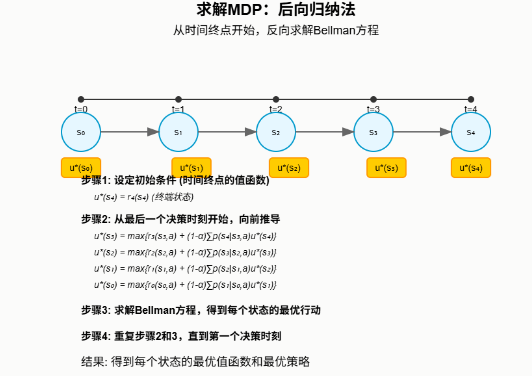
二、求解MDP
🔄后向归纳法 (Backward Induction):
- 最常用的求解有限时间地平线 MDP 的方法
- 从时间终点开始,反向求解 Bellman 方程
- 逐步计算每个决策时刻的最优行动

2.1 求解 MDP:价值迭代法和策略迭代法

2.2 策略迭代算法步骤
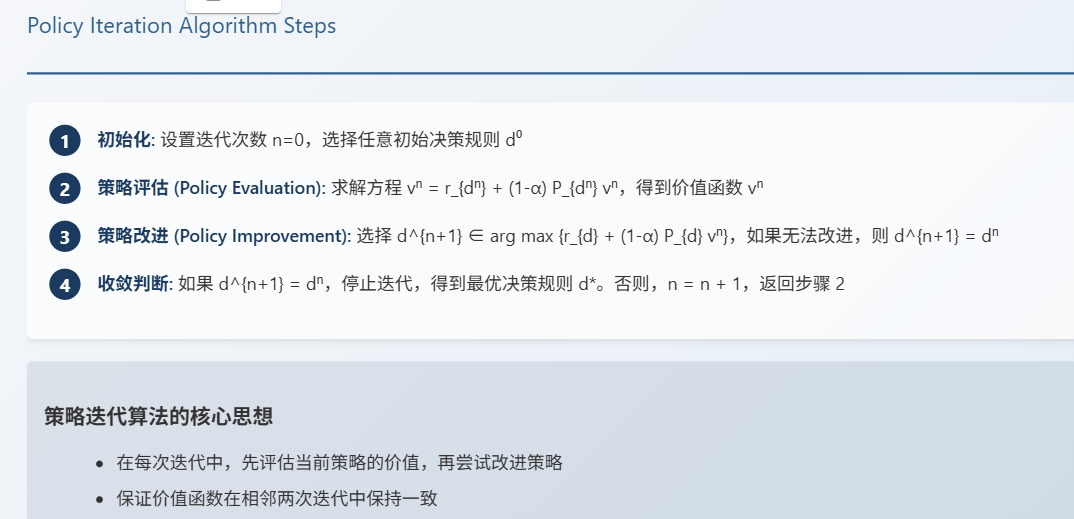
三、 案例研究:活体肝移植的最佳时机
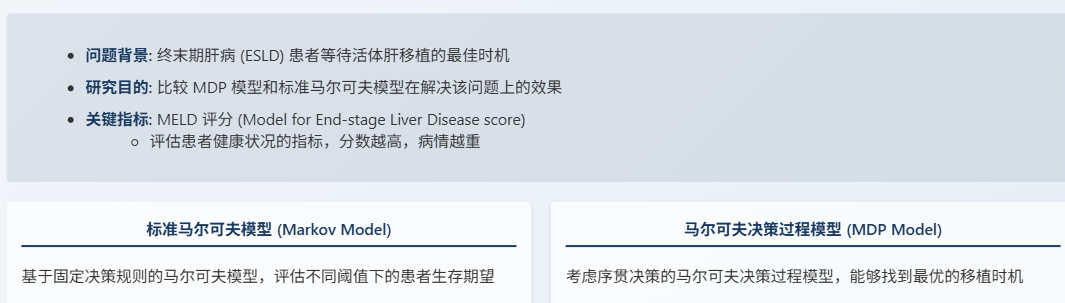

更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)