使用 Scipy 拟合 Weibull 分布
·
问题:使用 Scipy 拟合 Weibull 分布
我正在尝试重新创建最大似然分布拟合,我已经可以在 Matlab 和 R 中做到这一点,但现在我想使用 scipy。特别是,我想估计我的数据集的 Weibull 分布参数。
我试过这个:
import scipy.stats as s
import numpy as np
import matplotlib.pyplot as plt
def weib(x,n,a):
return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a)
data = np.loadtxt("stack_data.csv")
(loc, scale) = s.exponweib.fit_loc_scale(data, 1, 1)
print loc, scale
x = np.linspace(data.min(), data.max(), 1000)
plt.plot(x, weib(x, loc, scale))
plt.hist(data, data.max(), density=True)
plt.show()
得到这个:
(2.5827280639441961, 3.4955032285727947)
一个看起来像这样的分布:
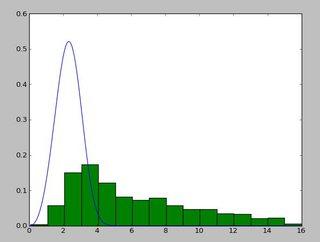
读完这篇http://www.johndcook.com/distributions_scipy.html后,我一直在使用exponweib。我还尝试了 scipy 中的其他 Weibull 函数(以防万一!)。
在 Matlab(使用分布拟合工具 - 见屏幕截图)和 R(使用 MASS 库函数fitdistr和 GAMLSS 包)中,我得到的 a(loc)和 b(scale)参数更像 1.58463497 5.93030013。我相信这三种方法都使用最大似然法进行分布拟合。
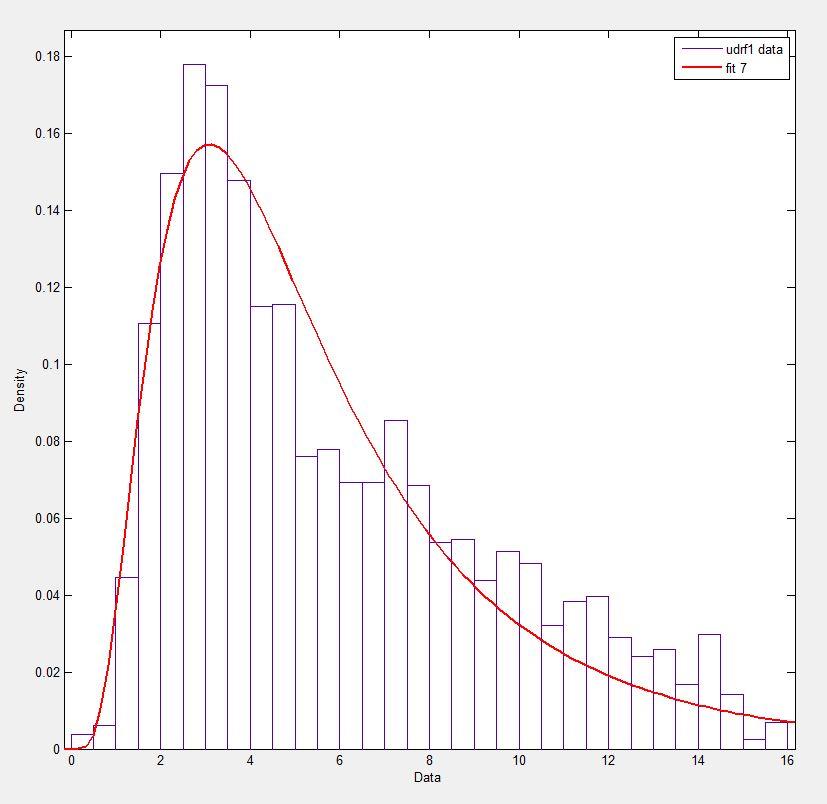
我已经在这里发布了我的数据如果你想试试看!为了完整起见,我使用的是 Python 2.7.5、Scipy 0.12.0、R 2.15.2 和 Matlab 2012b。
为什么我得到不同的结果!?
解答
我的猜测是,您想估计形状参数和 Weibull 分布的比例,同时保持位置固定。修复loc假设您的数据和分布的值为正,下限为零。
floc=0保持位置固定为零,f0=1保持指数威布尔的第一个形状参数固定为 1。
>>> stats.exponweib.fit(data, floc=0, f0=1)
[1, 1.8553346917584836, 0, 6.8820748596850905]
>>> stats.weibull_min.fit(data, floc=0)
[1.8553346917584836, 0, 6.8820748596850549]
与直方图相比,拟合看起来不错,但不是很好。参数估计值比您提到的来自 R 和 matlab 的估计值要高一些。
更新
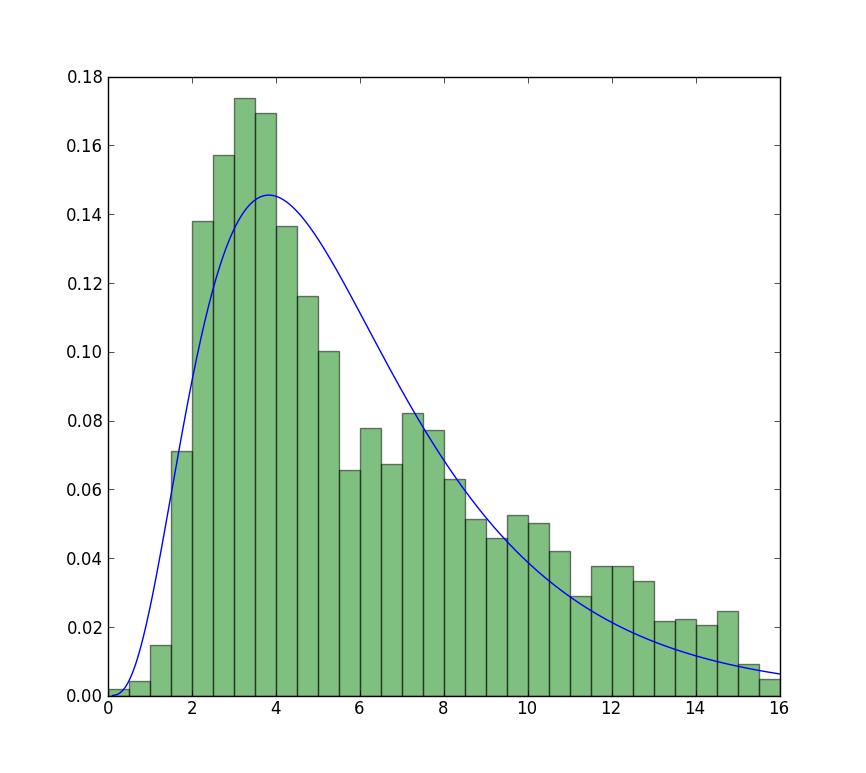
我能得到的最接近现在可用的图的是不受限制的拟合,但使用的是起始值。情节仍然没有那么高峰。注意前面没有 f 的 fit 值用作起始值。
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> plt.plot(data, stats.exponweib.pdf(data, *stats.exponweib.fit(data, 1, 1, scale=02, loc=0)))
>>> _ = plt.hist(data, bins=np.linspace(0, 16, 33), normed=True, alpha=0.5);
>>> plt.show()
更多推荐
 已为社区贡献126445条内容
已为社区贡献126445条内容







所有评论(0)