The matplotlib.pyplot.contour() function takes 3 input arrays X, Y and Z.
The arrays X and Y specify the x- and y-coordinates of points, while Z specifies the corresponding value of the function of interest evaluated at the points.
I understand that np.meshgrid() makes it easy to produce arrays which serve as arguments to contour():
X = np.arange(0,5,0.01)
Y = np.arange(0,3,0.01)
X_grid, Y_grid = np.meshgrid(X,Y)
Z_grid = X_grid**2 + Y_grid**2
plt.contour(X_grid, Y_grid, Z_grid) # Works fine
This works fine. And conveniently, this works fine too:
plt.contour(X, Y, Z_grid) # Works fine too
However, why is the Z input required to be a 2D-array?
Why is something like the following disallowed, even though it specifies all the same data aligned appropriately?
plt.contour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel()) # Disallowed
Also, what are the semantics when only Z is specified (without the corresponding X and Y)?
Looking at the documentation of contour one finds that there are a couple of ways to call this function, e.g. contour(Z) or contour(X,Y,Z). So you'll find that it does not require any X or Y values to be present at all.
However in order to plot a contour, the underlying grid must be known to the function. Matplotlib's contour is based on a rectangular grid. But even so, allowing contour(z), with z being a 1D array, would make it impossible to know how the field should be plotted. In the case of contour(Z) where Z is a 2D array, its shape unambiguously sets the grid for the plot.
Once that grid is known, it is rather unimportant whether optional X and Y arrays are flattened or not; which is actually what the documentation tells us:
X and Y must both be 2-D with the same shape as Z, or they must both be 1-D such that len(X) is the number of columns in Z and len(Y) is the number of rows in Z.
It is also pretty obvious that someting like plt.contour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel()) cannot produce a contour plot, because all the information about the grid shape is lost and there is no way the contour function could know how to interprete the data. E.g. if len(Z_grid.ravel()) == 12, the underlying grid's shape could be any of (1,12), (2,6), (3,4), (4,3), (6,2), (12,1).
A possible way out could of course be to allow for 1D arrays and introduce an argument shape, like plt.contour(x,y,z, shape=(6,2)). This however is not the case, so you have to live with the fact that Z needs to be 2D.
However, if you are looking for a way to obtain a countour plot with flattened (ravelled) arrays, this is possible using plt.tricontour().
plt.tricontour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel())
Here a triangular grid will be produced internally using a Delaunay Triangualation. Therefore even completely randomized points will produce a nice result, as can be seen in the following picture, where this is compared to the same random points given to contour.
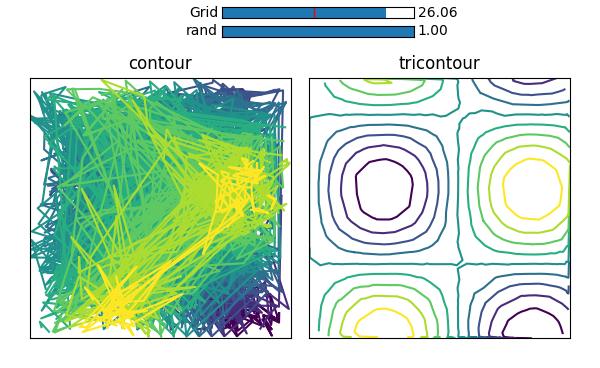
(Here is the code to produce this picture)







 已为社区贡献126446条内容
已为社区贡献126446条内容

所有评论(0)