I am trying to invert an interpolated function using scipy's interpolate function. Let's say I create an interpolated function,

import scipy.interpolate as interpolate
interpolatedfunction = interpolated.interp1d(xvariable,data,kind='cubic')

Is there some function that can find x when I specify a:

interpolatedfunction(x) == a

In other words, "I want my interpolated function to equal a; what is the value of xvariable such that my function is equal to a?"

I appreciate I can do this with some numerical scheme, but is there a more straightforward method? What if the interpolated function is multivalued in xvariable?

After creating an interpolated function interp_fn, you can find the value of x where interp_fn(x) == a by the roots of the function

interp_fn2 = lambda x: interp_fn(x) - a

There are number of options to find the roots in scipy.optimize. For instance, to use Newton's method with the initial value starting at 10:

from scipy import optimize

optimize.newton(interp_fn2, 10)

Actual example

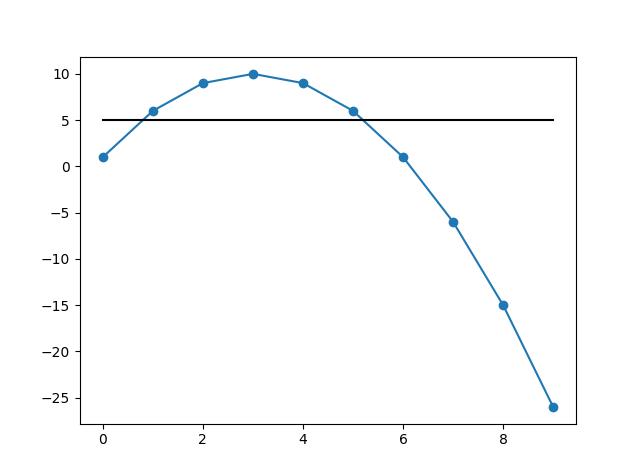
Create an interpolated function and then find the roots where fn(x) == 5

import numpy as np
from scipy import interpolate, optimize

x = np.arange(10)
y = 1 + 6*np.arange(10) - np.arange(10)**2
y2 = 5*np.ones_like(x)
plt.scatter(x,y)
plt.plot(x,y)
plt.plot(x,y2,'k-')
plt.show()

# create the interpolated function, and then the offset
# function used to find the roots

interp_fn = interpolate.interp1d(x, y, 'quadratic')
interp_fn2 = lambda x: interp_fn(x)-5

# to find the roots, we need to supply a starting value
# because there are more than 1 root in our range, we need 
# to supply multiple starting values.  They should be 
# fairly close to the actual root

root1, root2 = optimize.newton(interp_fn2, 1), optimize.newton(interp_fn2, 5)

root1, root2
# returns:
(0.76393202250021064, 5.2360679774997898)