I have a set of simulation data where I would like to find the lowest slope in n dimensions. The spacing of the data is constant along each dimension, but not all the same (I could change that for the sake of simplicity).

I can live with some numerical inaccuracy, especially towards the edges. I would heavily prefer not to generate a spline and use that derivative; just on the raw values would be sufficient.

It is possible to calculate the first derivative with numpy using the numpy.gradient() function.

import numpy as np

data = np.random.rand(30,50,40,20)
first_derivative = np.gradient(data)
# second_derivative = ??? <--- there be kudos (:

This is a comment regarding laplace versus the hessian matrix; this is no more a question but is meant to help understanding of future readers.

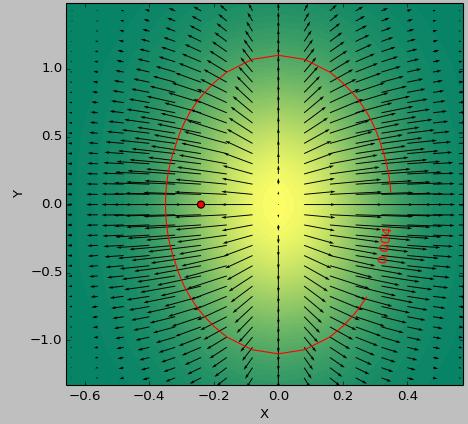
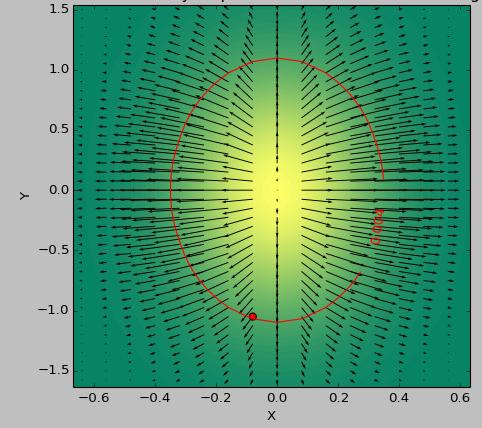
I use as a testcase a 2D function to determine the 'flattest' area below a threshold. The following pictures show the difference in results between using the minimum of second_derivative_abs = np.abs(laplace(data)) and the minimum of the following:

second_derivative_abs = np.zeros(data.shape)
hess = hessian(data)
# based on the function description; would [-1] be more appropriate? 
for i in hess[0]: # calculate a norm
    for j in i[0]:
        second_derivative_abs += j*j

The color scale depicts the functions values, the arrows depict the first derivative (gradient), the red dot the point closest to zero and the red line the threshold.

The generator function for the data was ( 1-np.exp(-10*xi**2 - yi**2) )/100.0 with xi, yi being generated with np.meshgrid.

Laplace:

Hessian:

The second derivatives are given by the Hessian matrix. Here is a Python implementation for ND arrays, that consists in applying the np.gradient twice and storing the output appropriately,

import numpy as np

def hessian(x):
    """
    Calculate the hessian matrix with finite differences
    Parameters:
       - x : ndarray
    Returns:
       an array of shape (x.dim, x.ndim) + x.shape
       where the array[i, j, ...] corresponds to the second derivative x_ij
    """
    x_grad = np.gradient(x) 
    hessian = np.empty((x.ndim, x.ndim) + x.shape, dtype=x.dtype) 
    for k, grad_k in enumerate(x_grad):
        # iterate over dimensions
        # apply gradient again to every component of the first derivative.
        tmp_grad = np.gradient(grad_k) 
        for l, grad_kl in enumerate(tmp_grad):
            hessian[k, l, :, :] = grad_kl
    return hessian

x = np.random.randn(100, 100, 100)
hessian(x)

Note that if you are only interested in the magnitude of the second derivatives, you could use the Laplace operator implemented by scipy.ndimage.filters.laplace, which is the trace (sum of diagonal elements) of the Hessian matrix.

Taking the smallest element of the the Hessian matrix could be used to estimate the lowest slope in any spatial direction.