回答问题

我目前正在为一门课程做一些频谱分析,尽管我们还没有明确地教过傅里叶变换。我一直在使用 scipy 和 numpy 中的各种 fft 算法来处理一些我知道答案应该是什么样子的数据

在这种情况下,它是一个 8kHz 载波频率的 AM 信号,顶部是 1kHz 调制正弦波,因此 fft 上应该有 3 个清晰的峰值

应用scipy.fftpack.rfft和numpy.fft.rfft时,我分别得到以下图:

Scipy:

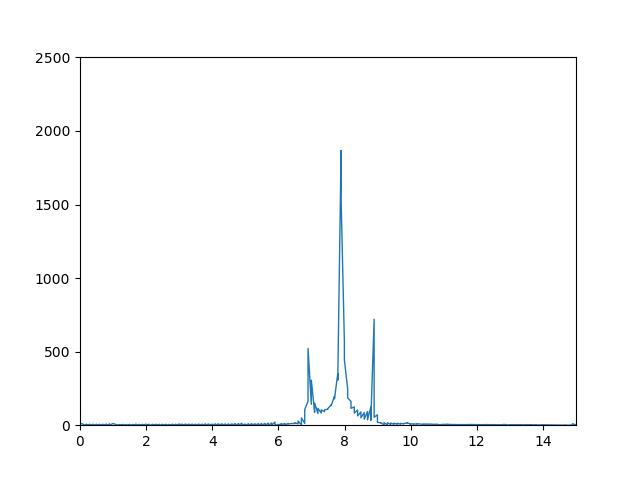
麻木:

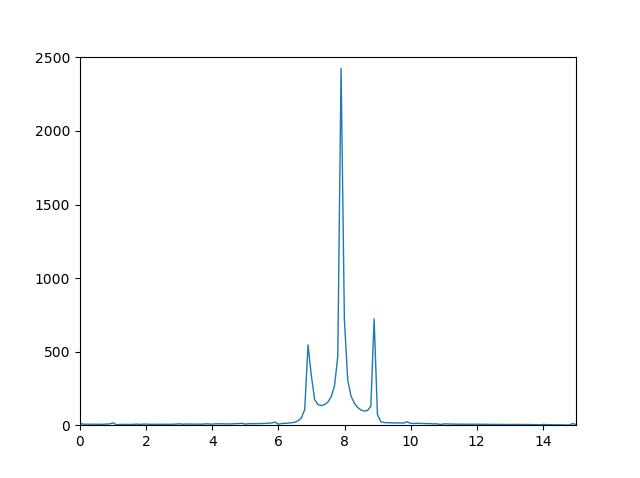
虽然 2 个 FFT 的形状与峰值之间的正确比率大致相同,但numpy看起来更平滑,而scipy的最大峰值略小,噪声更大。

我假设这很大程度上取决于离散傅立叶变换算法的不同应用,并且已经看到其他关于scipy实现如何在运行时更快的文章。但是我一直在徘徊,具体是什么导致了这种差异,哪一个实际上更准确?

编辑:用于生成图的代码:

data = pd.read_csv("./Waveforms/AM waveform Sine.csv", sep = ',', dtype = float)

data = data.as_matrix()
time = data[:,0]
voltage = data[:,1]/data[:,1].max() # normalise the values

#scipy plot:
plt.figure()
magnitude =  scipy.fftpack.rfft(voltage)
freq = scipy.fftpack.rfftfreq(len(time),np.diff(time)[0])
plt.figure()
plt.plot(freq, np.absolute(magnitude), lw = 1)
plt.ylim(0,2500)
plt.xlim(0,15)

#numpy plot
magnitude = np.fft.rfft(voltage)
freq = np.fft.rfftfreq(len(time),np.diff(time)[0])

plt.figure()
plt.plot(freq, np.absolute(magnitude), lw = 1)
plt.ylim(0,2500)
plt.xlim(0,15)

Answers

来自 NumPy 的rfft的文档:

退货:

out : 复杂的 ndarray

截断或补零的输入,沿轴指示的轴转换,如果未指定轴,则为最后一个。如果 n 是偶数,则变换轴的长度为 (n/2)+1。如果 n 为奇数,则长度为 (n+1)/2。

它没有明确写入,但“转换后的数据”在这里很复杂。

来自 SciPy 的文档rfft

z : 实数数组

返回的实数数组包含:

[y(0),Re(y(1)),Im(y(1)),...,Re(y(n/2))] 如果 n 是偶数

[y(0),Re(y(1)),Im(y(1)),...,Re(y(n/2)),Im(y(n/2))] 如果 n 是奇怪的

结论:存储不同。

首先,看一下magnitude的长度,这两种情况都会有所不同。为了清楚起见,我在下面举一个例子:

In [33]: data = np.random.random(size=8)

In [34]: np.fft.rfft(data)
Out[34]: 
array([ 3.33822983+0.j        ,  0.15879369+0.48542266j,
        0.00614876+0.03590621j, -0.67376592-0.69793372j,  1.51730861+0.j        ])

In [35]: scipy.fftpack.rfft(data)
Out[35]: 
array([ 3.33822983,  0.15879369,  0.48542266,  0.00614876,  0.03590621,
       -0.67376592, -0.69793372,  1.51730861])

在这两种情况下,第一个元素是所谓的“直流分量”(信号的平均值)。

然后,您可以在 SciPy 版本中识别 NumPy 版本的实部和虚部的连续性。