回答问题

我正在尝试在 Python 中实现一个 Reed-Solomon 编码器-解码器,支持对擦除和错误的解码,这让我发疯。

该实现目前支持仅解码错误或仅擦除,但不能同时解码两者(即使它低于 2*errors+erasures <u003d (n-k) 的理论界限)。

从 Blahut 的论文(这里和这里)看来,我们似乎只需要用擦除定位多项式初始化错误定位多项式,就可以隐式计算 Berlekamp-Massey 内的勘误定位多项式。

这种方法部分适用于我:当我有 2*errors+erasures < (n-k)/2 时,它可以工作,但实际上在调试之后它才有效,因为 BM 计算了一个错误定位器多项式,它得到与擦除定位器完全相同的值多项式(因为我们低于仅错误校正的限制),因此它通过 galois 域被截断,我们最终得到了擦除定位多项式的正确值(至少我是这样理解的,我可能是错的) .

但是,当我们超过 (n-k)/2 时,例如,如果 n u003d 20 且 k u003d 11,则我们可以纠正 (n-k)u003d9 个擦除符号,如果我们输入 5 个擦除,那么 BM 就会出错。如果我们输入 4 个擦除 + 1 个错误(我们仍然远低于界限,因为我们有 2*errors+erasures u003d 2+4 u003d 6 < 9),BM 仍然会出错。

我实现的 Berlekamp-Massey 的确切算法可以在这个演示文稿(第 15-17 页)中找到,但是可以在这里找到非常相似的描述和这里和这里我附上一份副本,数学描述:

现在,我将这个数学算法几乎完全复制到了 Python 代码中。我想要扩展它以支持擦除,我尝试使用擦除定位器初始化错误定位器 sigma:

def _berlekamp_massey(self, s, k=None, erasures_loc=None):
    '''Computes and returns the error locator polynomial (sigma) and the
    error evaluator polynomial (omega).
    If the erasures locator is specified, we will return an errors-and-erasures locator polynomial and an errors-and-erasures evaluator polynomial.
    The parameter s is the syndrome polynomial (syndromes encoded in a
    generator function) as returned by _syndromes. Don't be confused with
    the other s = (n-k)/2

    Notes:
    The error polynomial:
    E(x) = E_0 + E_1 x + ... + E_(n-1) x^(n-1)

    j_1, j_2, ..., j_s are the error positions. (There are at most s
    errors)

    Error location X_i is defined: X_i = a^(j_i)
    that is, the power of a corresponding to the error location

    Error magnitude Y_i is defined: E_(j_i)
    that is, the coefficient in the error polynomial at position j_i

    Error locator polynomial:
    sigma(z) = Product( 1 - X_i * z, i=1..s )
    roots are the reciprocals of the error locations
    ( 1/X_1, 1/X_2, ...)

    Error evaluator polynomial omega(z) is here computed at the same time as sigma, but it can also be constructed afterwards using the syndrome and sigma (see _find_error_evaluator() method).
    '''
    # For errors-and-erasures decoding, see: Blahut, Richard E. "Transform techniques for error control codes." IBM Journal of Research and development 23.3 (1979): 299-315. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.92.600&rep=rep1&type=pdf and also a MatLab implementation here: http://www.mathworks.com/matlabcentral/fileexchange/23567-reed-solomon-errors-and-erasures-decoder/content//RS_E_E_DEC.m
    # also see: Blahut, Richard E. "A universal Reed-Solomon decoder." IBM Journal of Research and Development 28.2 (1984): 150-158. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.84.2084&rep=rep1&type=pdf
    # or alternatively see the reference book by Blahut: Blahut, Richard E. Theory and practice of error control codes. Addison-Wesley, 1983.
    # and another good alternative book with concrete programming examples: Jiang, Yuan. A practical guide to error-control coding using Matlab. Artech House, 2010.
    n = self.n
    if not k: k = self.k

    # Initialize:
    if erasures_loc:
        sigma = [ Polynomial(erasures_loc.coefficients) ] # copy erasures_loc by creating a new Polynomial
        B = [ Polynomial(erasures_loc.coefficients) ]
    else:
        sigma =  [ Polynomial([GF256int(1)]) ] # error locator polynomial. Also called Lambda in other notations.
        B =    [ Polynomial([GF256int(1)]) ] # this is the error locator support/secondary polynomial, which is a funky way to say that it's just a temporary variable that will help us construct sigma, the error locator polynomial
    omega =  [ Polynomial([GF256int(1)]) ] # error evaluator polynomial. We don't need to initialize it with erasures_loc, it will still work, because Delta is computed using sigma, which itself is correctly initialized with erasures if needed.
    A =  [ Polynomial([GF256int(0)]) ] # this is the error evaluator support/secondary polynomial, to help us construct omega
    L =      [ 0 ] # necessary variable to check bounds (to avoid wrongly eliminating the higher order terms). For more infos, see https://www.cs.duke.edu/courses/spring11/cps296.3/decoding_rs.pdf
    M =      [ 0 ] # optional variable to check bounds (so that we do not mistakenly overwrite the higher order terms). This is not necessary, it's only an additional safe check. For more infos, see the presentation decoding_rs.pdf by Andrew Brown in the doc folder.

    # Polynomial constants:
    ONE = Polynomial(z0=GF256int(1))
    ZERO = Polynomial(z0=GF256int(0))
    Z = Polynomial(z1=GF256int(1)) # used to shift polynomials, simply multiply your poly * Z to shift

    s2 = ONE + s

    # Iteratively compute the polynomials 2s times. The last ones will be
    # correct
    for l in xrange(0, n-k):
        K = l+1
        # Goal for each iteration: Compute sigma[K] and omega[K] such that
        # (1 + s)*sigma[l] == omega[l] in mod z^(K)

        # For this particular loop iteration, we have sigma[l] and omega[l],
        # and are computing sigma[K] and omega[K]

        # First find Delta, the non-zero coefficient of z^(K) in
        # (1 + s) * sigma[l]
        # This delta is valid for l (this iteration) only
        Delta = ( s2 * sigma[l] ).get_coefficient(l+1) # Delta is also known as the Discrepancy, and is always a scalar (not a polynomial).
        # Make it a polynomial of degree 0, just for ease of computation with polynomials sigma and omega.
        Delta = Polynomial(x0=Delta)

        # Can now compute sigma[K] and omega[K] from
        # sigma[l], omega[l], B[l], A[l], and Delta
        sigma.append( sigma[l] - Delta * Z * B[l] )
        omega.append( omega[l] - Delta * Z * A[l] )

        # Now compute the next B and A
        # There are two ways to do this
        # This is based on a messy case analysis on the degrees of the four polynomials sigma, omega, A and B in order to minimize the degrees of A and B. For more infos, see https://www.cs.duke.edu/courses/spring10/cps296.3/decoding_rs_scribe.pdf
        # In fact it ensures that the degree of the final polynomials aren't too large.
        if Delta == ZERO or 2*L[l] > K \
            or (2*L[l] == K and M[l] == 0):
            # Rule A
            B.append( Z * B[l] )
            A.append( Z * A[l] )
            L.append( L[l] )
            M.append( M[l] )

        elif (Delta != ZERO and 2*L[l] < K) \
            or (2*L[l] == K and M[l] != 0):
            # Rule B
            B.append( sigma[l] // Delta )
            A.append( omega[l] // Delta )
            L.append( K - L[l] )
            M.append( 1 - M[l] )

        else:
            raise Exception("Code shouldn't have gotten here")

    return sigma[-1], omega[-1]

多项式和 GF256int 分别是 2^8 上的多项式和伽罗瓦域的通用实现。这些类是单元测试的,并且它们通常是错误证明的。 Reed-Solomon 的其他编码/解码方法也是如此,例如 Forney 和 Chien 搜索。可以在这里找到针对我正在谈论的问题的快速测试用例的完整代码:http://codepad.org/l2Qi0y8o

这是一个示例输出:

Encoded message:
hello world�ꐙ�Ī`>
-------
Erasures decoding:
Erasure locator: 189x^5 + 88x^4 + 222x^3 + 33x^2 + 251x + 1
Syndrome: 149x^9 + 113x^8 + 29x^7 + 231x^6 + 210x^5 + 150x^4 + 192x^3 + 11x^2 + 41x
Sigma: 189x^5 + 88x^4 + 222x^3 + 33x^2 + 251x + 1
Symbols positions that were corrected: [19, 18, 17, 16, 15]
('Decoded message: ', 'hello world', '\xce\xea\x90\x99\x8d\xc4\xaa`>')
Correctly decoded:  True
-------
Errors+Erasures decoding for the message with only erasures:
Erasure locator: 189x^5 + 88x^4 + 222x^3 + 33x^2 + 251x + 1
Syndrome: 149x^9 + 113x^8 + 29x^7 + 231x^6 + 210x^5 + 150x^4 + 192x^3 + 11x^2 + 41x
Sigma: 101x^10 + 139x^9 + 5x^8 + 14x^7 + 180x^6 + 148x^5 + 126x^4 + 135x^3 + 68x^2 + 155x + 1
Symbols positions that were corrected: [187, 141, 90, 19, 18, 17, 16, 15]
('Decoded message: ', '\xf4\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00.\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00P\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xe3\xe6\xffO> world', '\xce\xea\x90\x99\x8d\xc4\xaa`>')
Correctly decoded:  False
-------
Errors+Erasures decoding for the message with erasures and one error:
Erasure locator: 77x^4 + 96x^3 + 6x^2 + 206x + 1
Syndrome: 49x^9 + 107x^8 + x^7 + 109x^6 + 236x^5 + 15x^4 + 8x^3 + 133x^2 + 243x
Sigma: 38x^9 + 98x^8 + 239x^7 + 85x^6 + 32x^5 + 168x^4 + 92x^3 + 225x^2 + 22x + 1
Symbols positions that were corrected: [19, 18, 17, 16]
('Decoded message: ', "\xda\xe1'\xccA world", '\xce\xea\x90\x99\x8d\xc4\xaa`>')
Correctly decoded:  False

在这里,擦除解码总是正确的,因为它根本不使用 BM 来计算擦除定位器。通常,其他两个测试用例应该输出相同的 sigma,但它们根本不会。

当您比较前两个测试用例时,问题来自 BM 的事实在这里是公然的:校正子和擦除定位器是相同的,但得到的 sigma 完全不同(在第二个测试中,使用了 BM,而在不调用仅擦除 BM 的第一个测试用例)。

非常感谢您对我如何调试它的任何帮助或任何想法。请注意,您的答案可以是数学或代码,但请解释我的方法出了什么问题。

/编辑: 仍然没有找到正确实现勘误表 BM 解码器的方法(请参阅下面的答案)。赏金提供给任何可以解决问题(或至少引导我找到解决方案)的人。

/EDIT2: 傻我,对不起,我刚刚重新阅读了架构,发现我错过了分配L = r - L - erasures_count中的更改...我已经更新了代码来解决这个问题并重新接受了我的答案。

Answers

在阅读了大量的研究论文和书籍之后,我唯一找到答案的地方就是书中(可以在 Google Books上在线阅读,但不能以 PDF 格式提供):

“数据传输的代数码”,Blahut,Richard E.,2003 年,剑桥大学出版社。

以下是本书的一些摘录,其中详细描述了我实现的 Berlekamp-Massey 算法的准确描述(多项式运算的矩阵/向量化表示除外):

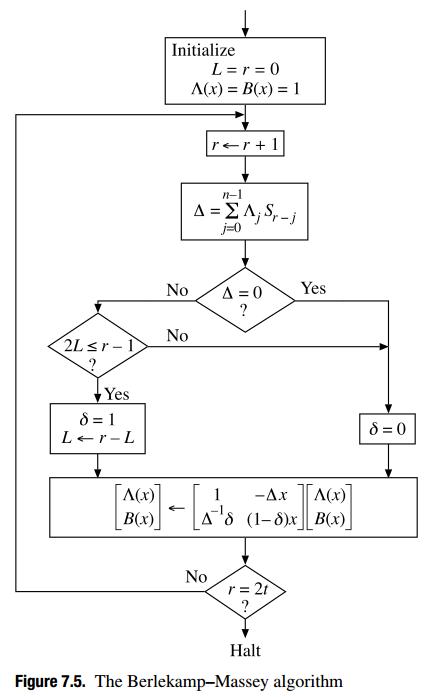
这是 Reed-Solomon 的勘误表(错误和擦除)Berlekamp-Massey 算法:

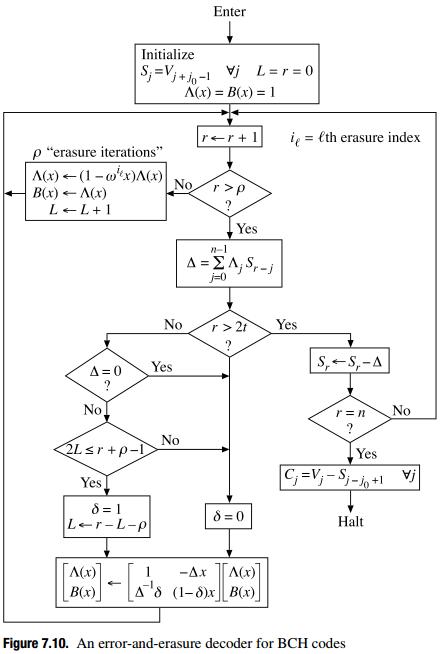
正如你所看到的——与通常的描述相反,你只需要用先前计算的擦除定位多项式的值来初始化 Lambda,即错误定位多项式**——你还需要跳过前 v 次迭代,其中 v 是擦除次数。请注意,它不等同于跳过最后 v 次迭代:您需要跳过前 v 次迭代,因为 r(迭代计数器,在我的实现中为 K)不仅用于计算迭代次数,还用于生成正确的差异因子 Delta。

以下是修改后的结果代码,以支持擦除以及高达v+2*e <= (n-k)的错误:

def _berlekamp_massey(self, s, k=None, erasures_loc=None, erasures_eval=None, erasures_count=0):
    '''Computes and returns the errata (errors+erasures) locator polynomial (sigma) and the
    error evaluator polynomial (omega) at the same time.
    If the erasures locator is specified, we will return an errors-and-erasures locator polynomial and an errors-and-erasures evaluator polynomial, else it will compute only errors. With erasures in addition to errors, it can simultaneously decode up to v+2e <= (n-k) where v is the number of erasures and e the number of errors.
    Mathematically speaking, this is equivalent to a spectral analysis (see Blahut, "Algebraic Codes for Data Transmission", 2003, chapter 7.6 Decoding in Time Domain).
    The parameter s is the syndrome polynomial (syndromes encoded in a
    generator function) as returned by _syndromes.

    Notes:
    The error polynomial:
    E(x) = E_0 + E_1 x + ... + E_(n-1) x^(n-1)

    j_1, j_2, ..., j_s are the error positions. (There are at most s
    errors)

    Error location X_i is defined: X_i = α^(j_i)
    that is, the power of α (alpha) corresponding to the error location

    Error magnitude Y_i is defined: E_(j_i)
    that is, the coefficient in the error polynomial at position j_i

    Error locator polynomial:
    sigma(z) = Product( 1 - X_i * z, i=1..s )
    roots are the reciprocals of the error locations
    ( 1/X_1, 1/X_2, ...)

    Error evaluator polynomial omega(z) is here computed at the same time as sigma, but it can also be constructed afterwards using the syndrome and sigma (see _find_error_evaluator() method).

    It can be seen that the algorithm tries to iteratively solve for the error locator polynomial by
    solving one equation after another and updating the error locator polynomial. If it turns out that it
    cannot solve the equation at some step, then it computes the error and weights it by the last
    non-zero discriminant found, and delays the weighted result to increase the polynomial degree
    by 1. Ref: "Reed Solomon Decoder: TMS320C64x Implementation" by Jagadeesh Sankaran, December 2000, Application Report SPRA686

    The best paper I found describing the BM algorithm for errata (errors-and-erasures) evaluator computation is in "Algebraic Codes for Data Transmission", Richard E. Blahut, 2003.
    '''
    # For errors-and-erasures decoding, see: "Algebraic Codes for Data Transmission", Richard E. Blahut, 2003 and (but it's less complete): Blahut, Richard E. "Transform techniques for error control codes." IBM Journal of Research and development 23.3 (1979): 299-315. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.92.600&rep=rep1&type=pdf and also a MatLab implementation here: http://www.mathworks.com/matlabcentral/fileexchange/23567-reed-solomon-errors-and-erasures-decoder/content//RS_E_E_DEC.m
    # also see: Blahut, Richard E. "A universal Reed-Solomon decoder." IBM Journal of Research and Development 28.2 (1984): 150-158. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.84.2084&rep=rep1&type=pdf
    # and another good alternative book with concrete programming examples: Jiang, Yuan. A practical guide to error-control coding using Matlab. Artech House, 2010.
    n = self.n
    if not k: k = self.k

    # Initialize, depending on if we include erasures or not:
    if erasures_loc:
        sigma = [ Polynomial(erasures_loc.coefficients) ] # copy erasures_loc by creating a new Polynomial, so that we initialize the errata locator polynomial with the erasures locator polynomial.
        B = [ Polynomial(erasures_loc.coefficients) ]
        omega =  [ Polynomial(erasures_eval.coefficients) ] # to compute omega (the evaluator polynomial) at the same time, we also need to initialize it with the partial erasures evaluator polynomial
        A =  [ Polynomial(erasures_eval.coefficients) ] # TODO: fix the initial value of the evaluator support polynomial, because currently the final omega is not correct (it contains higher order terms that should be removed by the end of BM)
    else:
        sigma =  [ Polynomial([GF256int(1)]) ] # error locator polynomial. Also called Lambda in other notations.
        B =    [ Polynomial([GF256int(1)]) ] # this is the error locator support/secondary polynomial, which is a funky way to say that it's just a temporary variable that will help us construct sigma, the error locator polynomial
        omega =  [ Polynomial([GF256int(1)]) ] # error evaluator polynomial. We don't need to initialize it with erasures_loc, it will still work, because Delta is computed using sigma, which itself is correctly initialized with erasures if needed.
        A =  [ Polynomial([GF256int(0)]) ] # this is the error evaluator support/secondary polynomial, to help us construct omega
    L = [ 0 ] # update flag: necessary variable to check when updating is necessary and to check bounds (to avoid wrongly eliminating the higher order terms). For more infos, see https://www.cs.duke.edu/courses/spring11/cps296.3/decoding_rs.pdf
    M = [ 0 ] # optional variable to check bounds (so that we do not mistakenly overwrite the higher order terms). This is not necessary, it's only an additional safe check. For more infos, see the presentation decoding_rs.pdf by Andrew Brown in the doc folder.

    # Fix the syndrome shifting: when computing the syndrome, some implementations may prepend a 0 coefficient for the lowest degree term (the constant). This is a case of syndrome shifting, thus the syndrome will be bigger than the number of ecc symbols (I don't know what purpose serves this shifting). If that's the case, then we need to account for the syndrome shifting when we use the syndrome such as inside BM, by skipping those prepended coefficients.
    # Another way to detect the shifting is to detect the 0 coefficients: by definition, a syndrome does not contain any 0 coefficient (except if there are no errors/erasures, in this case they are all 0). This however doesn't work with the modified Forney syndrome (that we do not use in this lib but it may be implemented in the future), which set to 0 the coefficients corresponding to erasures, leaving only the coefficients corresponding to errors.
    synd_shift = 0
    if len(s) > (n-k): synd_shift = len(s) - (n-k)

    # Polynomial constants:
    ONE = Polynomial(z0=GF256int(1))
    ZERO = Polynomial(z0=GF256int(0))
    Z = Polynomial(z1=GF256int(1)) # used to shift polynomials, simply multiply your poly * Z to shift

    # Precaching
    s2 = ONE + s

    # Iteratively compute the polynomials n-k-erasures_count times. The last ones will be correct (since the algorithm refines the error/errata locator polynomial iteratively depending on the discrepancy, which is kind of a difference-from-correctness measure).
    for l in xrange(0, n-k-erasures_count): # skip the first erasures_count iterations because we already computed the partial errata locator polynomial (by initializing with the erasures locator polynomial)
        K = erasures_count+l+synd_shift # skip the FIRST erasures_count iterations (not the last iterations, that's very important!)

        # Goal for each iteration: Compute sigma[l+1] and omega[l+1] such that
        # (1 + s)*sigma[l] == omega[l] in mod z^(K)

        # For this particular loop iteration, we have sigma[l] and omega[l],
        # and are computing sigma[l+1] and omega[l+1]

        # First find Delta, the non-zero coefficient of z^(K) in
        # (1 + s) * sigma[l]
        # Note that adding 1 to the syndrome s is not really necessary, you can do as well without.
        # This delta is valid for l (this iteration) only
        Delta = ( s2 * sigma[l] ).get_coefficient(K) # Delta is also known as the Discrepancy, and is always a scalar (not a polynomial).
        # Make it a polynomial of degree 0, just for ease of computation with polynomials sigma and omega.
        Delta = Polynomial(x0=Delta)

        # Can now compute sigma[l+1] and omega[l+1] from
        # sigma[l], omega[l], B[l], A[l], and Delta
        sigma.append( sigma[l] - Delta * Z * B[l] )
        omega.append( omega[l] - Delta * Z * A[l] )

        # Now compute the next support polynomials B and A
        # There are two ways to do this
        # This is based on a messy case analysis on the degrees of the four polynomials sigma, omega, A and B in order to minimize the degrees of A and B. For more infos, see https://www.cs.duke.edu/courses/spring10/cps296.3/decoding_rs_scribe.pdf
        # In fact it ensures that the degree of the final polynomials aren't too large.
        if Delta == ZERO or 2*L[l] > K+erasures_count \
            or (2*L[l] == K+erasures_count and M[l] == 0):
        #if Delta == ZERO or len(sigma[l+1]) <= len(sigma[l]): # another way to compute when to update, and it doesn't require to maintain the update flag L
            # Rule A
            B.append( Z * B[l] )
            A.append( Z * A[l] )
            L.append( L[l] )
            M.append( M[l] )

        elif (Delta != ZERO and 2*L[l] < K+erasures_count) \
            or (2*L[l] == K+erasures_count and M[l] != 0):
        # elif Delta != ZERO and len(sigma[l+1]) > len(sigma[l]): # another way to compute when to update, and it doesn't require to maintain the update flag L
            # Rule B
            B.append( sigma[l] // Delta )
            A.append( omega[l] // Delta )
            L.append( K - L[l] ) # the update flag L is tricky: in Blahut's schema, it's mandatory to use `L = K - L - erasures_count` (and indeed in a previous draft of this function, if you forgot to do `- erasures_count` it would lead to correcting only 2*(errors+erasures) <= (n-k) instead of 2*errors+erasures <= (n-k)), but in this latest draft, this will lead to a wrong decoding in some cases where it should correctly decode! Thus you should try with and without `- erasures_count` to update L on your own implementation and see which one works OK without producing wrong decoding failures.
            M.append( 1 - M[l] )

        else:
            raise Exception("Code shouldn't have gotten here")

    # Hack to fix the simultaneous computation of omega, the errata evaluator polynomial: because A (the errata evaluator support polynomial) is not correctly initialized (I could not find any info in academic papers). So at the end, we get the correct errata evaluator polynomial omega + some higher order terms that should not be present, but since we know that sigma is always correct and the maximum degree should be the same as omega, we can fix omega by truncating too high order terms.
    if omega[-1].degree > sigma[-1].degree: omega[-1] = Polynomial(omega[-1].coefficients[-(sigma[-1].degree+1):])

    # Return the last result of the iterations (since BM compute iteratively, the last iteration being correct - it may already be before, but we're not sure)
    return sigma[-1], omega[-1]

def _find_erasures_locator(self, erasures_pos):
    '''Compute the erasures locator polynomial from the erasures positions (the positions must be relative to the x coefficient, eg: "hello worldxxxxxxxxx" is tampered to "h_ll_ worldxxxxxxxxx" with xxxxxxxxx being the ecc of length n-k=9, here the string positions are [1, 4], but the coefficients are reversed since the ecc characters are placed as the first coefficients of the polynomial, thus the coefficients of the erased characters are n-1 - [1, 4] = [18, 15] = erasures_loc to be specified as an argument.'''
    # See: http://ocw.usu.edu/Electrical_and_Computer_Engineering/Error_Control_Coding/lecture7.pdf and Blahut, Richard E. "Transform techniques for error control codes." IBM Journal of Research and development 23.3 (1979): 299-315. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.92.600&rep=rep1&type=pdf and also a MatLab implementation here: http://www.mathworks.com/matlabcentral/fileexchange/23567-reed-solomon-errors-and-erasures-decoder/content//RS_E_E_DEC.m
    erasures_loc = Polynomial([GF256int(1)]) # just to init because we will multiply, so it must be 1 so that the multiplication starts correctly without nulling any term
    # erasures_loc is very simple to compute: erasures_loc = prod(1 - x*alpha[j]**i) for i in erasures_pos and where alpha is the alpha chosen to evaluate polynomials (here in this library it's gf(3)). To generate c*x where c is a constant, we simply generate a Polynomial([c, 0]) where 0 is the constant and c is positionned to be the coefficient for x^1. See https://en.wikipedia.org/wiki/Forney_algorithm#Erasures
    for i in erasures_pos:
        erasures_loc = erasures_loc * (Polynomial([GF256int(1)]) - Polynomial([GF256int(self.generator)**i, 0]))
    return erasures_loc

注意:Sigma、Omega、A、B、L 和 M 都是多项式列表(因此我们保留了我们在每次迭代中计算的所有中间多项式的全部历史)。这当然可以优化,因为我们真的只需要Sigma[l]、Sigma[l-1]、Omega[l]、Omega[l-1]、A[l]、B[l]、L[l]和M[l](所以只有Sigma和Omega需要将之前的迭代保留在内存中,其他变量不需要)。

Note2:更新标志 L 很棘手:在某些实现中,像在 Blahut 的模式中那样做会在解码时导致错误的失败。在我过去的实现中,必须使用L = K - L - erasures_count将错误和擦除正确解码到 Singleton 界限,但在我最新的实现中,我必须使用L = K - L(即使存在擦除)以避免错误解码失败。你应该在你自己的实现上都尝试一下,看看哪一个不会产生任何错误的解码失败。有关更多信息,请参阅下面的问题。

该算法的唯一问题是它没有描述如何同时计算 Omega,即错误评估多项式(本书描述了如何初始化 Omega 仅用于错误,而不是在解码错误和擦除时)。我尝试了几种变体和上述工作,但并不完全:最后,欧米茄将包括本应取消的高阶项。可能 Omega 或 A 错误评估器支持多项式,没有用好的值初始化。

但是,您可以通过修剪太高阶项的 Omega 多项式来解决这个问题(因为它应该具有与 Lambda/Sigma 相同的次数):

if omega[-1].degree > sigma[-1].degree: omega[-1] = Polynomial(omega[-1].coefficients[-(sigma[-1].degree+1):])

或者,您可以在 BM 之后使用勘误表定位器 Lambda/Sigma 完全从头计算 Omega,它始终可以正确计算:

def _find_error_evaluator(self, synd, sigma, k=None):
    '''Compute the error (or erasures if you supply sigma=erasures locator polynomial) evaluator polynomial Omega from the syndrome and the error/erasures/errata locator Sigma. Omega is already computed at the same time as Sigma inside the Berlekamp-Massey implemented above, but in case you modify Sigma, you can recompute Omega afterwards using this method, or just ensure that Omega computed by BM is correct given Sigma (as long as syndrome and sigma are correct, omega will be correct).'''
    n = self.n
    if not k: k = self.k

    # Omega(x) = [ Synd(x) * Error_loc(x) ] mod x^(n-k+1) -- From Blahut, Algebraic codes for data transmission, 2003
    return (synd * sigma) % Polynomial([GF256int(1)] + [GF256int(0)] * (n-k+1)) # Note that you should NOT do (1+Synd(x)) as can be seen in some books because this won't work with all primitive generators.

我正在以下关于 CSTheory的问题中寻找更好的解决方案。

/编辑: 我将描述我遇到的一些问题以及如何解决它们:

• 不要忘记使用擦除定位器多项式初始化错误定位器多项式(您可以轻松地从校正子和擦除位置计算)。

• 如果您只能解码错误并且只能完美擦除,但仅限于2*errors + erasures <= (n-k)/2,那么您忘记跳过前 v 次迭代。

• 如果您可以同时解码擦除和错误但最高可达2*(errors+erasures) <= (n-k),那么您忘记更新 L 的分配:L = i+1 - L - erasures_count而不是L = i+1 - L。但这实际上可能会使您的解码器在某些情况下失败,具体取决于您如何实现解码器,请参阅下一点。

• 我的第一个解码器仅限于一个生成器/素数多项式/fcr,但是当我将其更新为通用并添加严格的单元测试时,解码器在不应该的情况下失败了。似乎 Blahut 的上述模式关于 L(更新标志)是错误的:它必须使用L = K - L而不是L = K - L - erasures_count更新,因为这有时会导致解码器失败,即使我们处于单例绑定之下(因此我们应该正确解码!)。计算L = K - L不仅可以解决这些解码问题,而且它还会给出与不使用更新标志 L 的替代更新方式完全相同的结果(即条件if Delta == ZERO or len(sigma[l+1]) <= len(sigma[l]):),这一事实似乎证实了这一点。但这很奇怪:在我过去的实现中,L = K - L - erasures_count对于错误和擦除解码是强制性的,但现在它似乎会产生错误的失败。因此,您应该尝试使用和不使用您自己的实现,以及其中一个或另一个是否会为您产生错误的失败。

• 注意条件2*L[l] > K变为2*L[l] > K+erasures_count。如果不首先添加条件+erasures_count,您可能不会注意到任何副作用,但在某些情况下,解码会在不应该的情况下失败。

• 如果您只能修复一个错误或擦除,请检查您的条件是2*L[l] > K+erasures_count而不是2*L[l] >= K+erasures_count(注意>而不是>=)。

• 如果您可以纠正2*errors + erasures <= (n-k-2)(略低于限制,例如,如果您有 10 个 ecc 符号,则只能纠正 4 个错误而不是正常的 5 个)然后检查您的综合症和 BM 算法中的循环:如果综合症以0 常数项 x^0 的系数(有时在书中建议),然后您的综合症被转移,然后您在 BM 内的循环必须从1开始,如果没有转移,则在n-k+1而不是0:(n-k)结束。

• 如果您可以更正除最后一个(最后一个 ecc 符号)之外的每个符号,请检查您的范围,特别是在您的 Chien 搜索中:您不应该评估从 alpha^0 到 alpha^255 而是从 alpha^1 的错误定位器多项式到 alpha^256。