回答问题

哪些因素决定了multiprocessing.Pool.map()等方法的最佳chunksize参数?.map()方法似乎对其默认块大小使用任意启发式(解释如下);是什么激发了这种选择,是否有基于某些特定情况/设置的更周到的方法?

示例 - 说我是:

• 将iterable传递给具有约 1500 万个元素的.map();

• 在一台 24 核的机器上工作,在multiprocessing.Pool()中使用默认的processes = os.cpu_count()。

我的幼稚想法是给 24 名工人中的每人一个相同大小的块,即15_000_000 / 24或 625,000。大块应在充分利用所有工人的同时减少营业额/开销。但这似乎遗漏了为每个工人提供大批量的一些潜在缺点。这是一张不完整的照片,我错过了什么?

---

我的部分问题源于chunksize=None的默认逻辑:.map()和.starmap()都调用.map_async(),如下所示:

def _map_async(self, func, iterable, mapper, chunksize=None, callback=None,
               error_callback=None):
    # ... (materialize `iterable` to list if it's an iterator)
    if chunksize is None:
        chunksize, extra = divmod(len(iterable), len(self._pool) * 4)  # ????
        if extra:
            chunksize += 1
    if len(iterable) == 0:
        chunksize = 0

divmod(len(iterable), len(self._pool) * 4)背后的逻辑是什么?这意味着块大小将更接近15_000_000 / (24 * 4) == 156_250。将len(self._pool)乘以 4 的目的是什么?

这使得生成的块大小比我上面的“幼稚逻辑”小 4 倍,这只是将可迭代的长度除以pool._pool中的工人数量。

最后,还有来自.imap()上的 Python 文档的片段进一步激发了我的好奇心:

chunksize参数与map()方法使用的参数相同。对于非常长的迭代,使用较大的chunksize值可以使作业完成快比使用默认值 1 快。

祖兹 100033 * *

有帮助但有点太高级的相关答案:Python 多处理:为什么大块大小更慢?。

Answers

简答

Pool 的 chunksize-algorithm 是一种启发式算法。它为您尝试填充到 Pool 方法中的所有可以想象的问题场景提供了一个简单的解决方案。因此,它无法针对任何特定场景进行优化。

该算法将可迭代对象任意划分为大约四倍于幼稚方法的块。更多的块意味着更多的开销,但增加了调度的灵活性。这个答案将如何显示,这平均会导致更高的工人利用率,但_没有_保证每个案例的总计算时间更短。

“很高兴知道”,您可能会想,“但是知道这一点如何帮助我解决具体的多处理问题?”好吧,它没有。更诚实的简短答案是“没有简短答案”、“多处理很复杂”和“取决于情况”。观察到的症状可能有不同的根源,即使对于类似的情况也是如此。

这个答案试图为您提供基本概念,帮助您更清楚地了解 Pool 的调度黑盒。它还尝试为您提供一些手头的基本工具,用于识别和避免与块大小相关的潜在悬崖。

---

目录

第一部分

1. 定义

2. 并行化目标

3. 并行化场景

4. Chunksize > 1 的风险

5. Pool 的 Chunksize-Algorithm

6.量化算法效率

6.1 型号

6.2 并行调度

6.3 效率

6.3.1 绝对分配效率(ADE)

6.3.2 相对分配效率(RDE)

第二部分

7. Naive vs. Pool 的 Chunksize-Algorithm

8. 现实检查

9. 结论

有必要首先澄清一些重要的术语。

---

1.定义

大块

这里的一个块是在池方法调用中指定的iterable-argument 的一部分。如何计算块大小以及这会产生什么影响,是这个答案的主题。

任务

下图可以看到任务在工作进程中的数据物理表示。

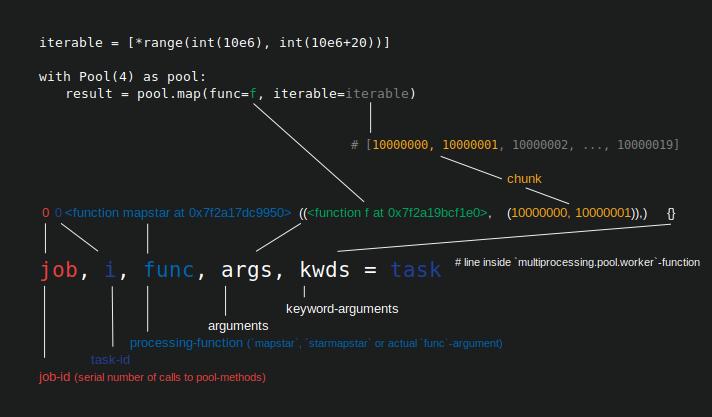
该图显示了对pool.map()的示例调用,沿一行代码显示,取自multiprocessing.pool.worker函数,其中从inqueue读取的任务被解包。worker是池工作进程的MainThread中的底层主函数。 pool-method 中指定的func- 参数将仅匹配worker- 函数中的func- 变量,用于apply_async等单调用方法以及imap和chunksize=1。对于带有chunksize-参数的池方法的其余部分,处理函数func将是映射器函数(mapstar或starmapstar)。此函数将用户指定的func-参数映射到可迭代的传输块的每个元素(-->“map-tasks”)。所花费的时间将任务也定义为工作单元。

抛光

虽然在multiprocessing.pool中使用“任务”一词来处理一个块的 whole 处理与multiprocessing.pool中的代码相匹配,但没有迹象表明如何对用户指定的func进行 single call,将块的一个元素作为参数,应该参考。为了避免命名冲突引起的混淆(想想池的__init__-方法的maxtasksperchild-参数),这个答案将任务中的单个工作单元称为 taskel。

taskel(来自task + element)是task 中的最小工作单元。它是使用Pool- 方法的func- 参数指定的函数的单次执行,使用从传输的块的单个元素获得的参数调用。一个 task 由chunksizetaskels 组成。

并行化开销 (PO)

PO 由 Python 内部开销和进程间通信 (IPC) 开销组成。 Python 中的每个任务开销伴随着打包和解包任务及其结果所需的代码。 IPC 开销伴随着必要的线程同步和不同地址空间之间的数据复制(需要两个复制步骤:父 -> 队列 -> 子)。 IPC 开销的数量取决于操作系统、硬件和数据大小,这使得对影响的概括变得困难。

zoz100036 * *

2.并行化目标

使用多处理时,我们的总体目标(显然)是最小化所有任务的总处理时间。为了达到这个总体目标,我们的技术目标需要优化硬件资源的利用率。

实现技术目标的一些重要子目标是:

• 最小化并行化开销(最著名,但并不孤单:IPC)

• 所有 cpu 核心的高利用率

• 限制内存使用以防止操作系统过度分页(垃圾)

首先,这些任务需要计算量足够大(密集),以_赚回_我们必须为并行化支付的 PO。 PO 的相关性随着每个任务的绝对计算时间的增加而降低。或者,换句话说,您的问题的绝对计算时间_per taskel_ 越大,减少 PO 的需求就越不相关。如果您的计算每个任务需要几个小时,那么 IPC 开销相比之下可以忽略不计。这里的主要关注点是防止在所有任务分发后空闲的工作进程。保持所有内核加载意味着,我们尽可能地并行化。

---

3.并行化场景

哪些因素决定了 multiprocessing.Pool.map() 等方法的最佳块大小参数

有问题的主要因素是我们的单个任务可能会_改变_多少计算时间。顾名思义,最佳块大小的选择由每个任务的计算时间的变异系数(CV)决定。

根据这种变化的程度,规模上的两种极端情况是:

1. 所有任务需要完全相同的计算时间。

2. taskel 可能需要几秒钟或几天才能完成。

为了更好地记忆,我将这些场景称为:

1. 密集场景

2. 宽场景

密集场景

在密集场景中,最好一次分发所有任务,以将必要的 IPC 和上下文切换保持在最低限度。这意味着我们只想创建尽可能多的块,尽可能多的工作进程。如上所述,PO 的权重随着每个任务的计算时间的缩短而增加。

为了获得最大吞吐量,我们还希望所有工作进程都处于忙碌状态,直到所有任务都处理完毕(没有空闲的工作进程)。为此目标,分布式块的大小应该相等或接近。

宽场景

Wide Scenario 的主要示例是优化问题,其中结果要么快速收敛,要么计算可能需要数小时,甚至数天。通常,在这种情况下,一个任务将包含哪些“轻任务”和“重任务”的混合是不可预测的,因此不建议一次在一个任务批次中分配太多任务。一次分配更少的任务意味着增加调度的灵活性。这是实现我们所有内核高利用率的子目标所必需的。

如果默认情况下Pool方法将针对密集场景进行完全优化,那么它们将越来越多地为靠近宽场景的每个问题创建次优时序。

---

4. Chunksize > 1 的风险

考虑这个 Wide Scenario-iterable 的简化伪代码示例,我们希望将其传递到池方法中:

good_luck_iterable = [60, 60, 86400, 60, 86400, 60, 60, 84600]

我们假装以秒为单位查看所需的计算时间,而不是实际值,为简单起见,仅为 1 分钟或 1 天。我们假设池中有四个工作进程(在四个核心上)并且chunksize设置为2。因为订单将被保留,所以发送给工作人员的块将是这些:

[(60, 60), (86400, 60), (86400, 60), (60, 84600)]

由于我们有足够的工人并且计算时间足够长,我们可以说,每个工人进程首先都会得到一个块来工作。 (这不一定是快速完成任务的情况)。进一步我们可以说,整个处理大约需要 86400+60 秒,因为这是这个人工场景中一个块的最高总计算时间,我们只分配一次块。

现在考虑这个可迭代对象,与前一个可迭代对象相比,它只有一个元素切换其位置:

bad_luck_iterable = [60, 60, 86400, 86400, 60, 60, 60, 84600]

...以及相应的块:

[(60, 60), (86400, 86400), (60, 60), (60, 84600)]

不幸的是,我们的迭代排序几乎使我们的总处理时间翻了一番(86400+86400)!获得恶意 (86400, 86400) 块的工人正在阻止其任务中的第二个重型任务分配给已经完成 (60, 60) 块的空闲工人之一。如果我们设置chunksize=1,我们显然不会冒这样不愉快的结果的风险。

这是更大块的风险。随着更大的块大小,我们用调度灵活性换取更少的开销,在上述情况下,这是一个糟糕的交易。

我们将如何在第 6 章中看到。量化算法效率,更大的块也可能导致密集场景的次优结果。

---

5.池的块大小算法

下面您将在源代码中找到该算法的略微修改版本。如您所见,我将下半部分切掉并包装成一个函数,用于在外部计算chunksize参数。我还用factor参数替换了4并将len()调用外包。

# mp_utils.py

def calc_chunksize(n_workers, len_iterable, factor=4):
    """Calculate chunksize argument for Pool-methods.

    Resembles source-code within `multiprocessing.pool.Pool._map_async`.
    """
    chunksize, extra = divmod(len_iterable, n_workers * factor)
    if extra:
        chunksize += 1
    return chunksize

为了确保我们都在同一个页面上,这是divmod所做的:

divmod(x, y)是一个返回(x//y, x%y)的内置函数。x // y是地板除法,从x / y返回向下舍入的商,而x % y是从x / y返回余数的模运算。因此,例如divmod(10, 3)返回(3, 1)。

现在,当您查看chunksize, extra = divmod(len_iterable, n_workers * 4)时,您会注意到n_workers是x / y中的除数y并乘以4,稍后无需通过if extra: chunksize +=1进一步调整,导致初始块大小_至少_比其他情况小四倍(对于len_iterable >= n_workers * 4) .

要查看乘以4对中间块大小结果的影响,请考虑以下函数:

def compare_chunksizes(len_iterable, n_workers=4):
    """Calculate naive chunksize, Pool's stage-1 chunksize and the chunksize
    for Pool's complete algorithm. Return chunksizes and the real factors by
    which naive chunksizes are bigger.
    """
    cs_naive = len_iterable // n_workers or 1  # naive approach
    cs_pool1 = len_iterable // (n_workers * 4) or 1  # incomplete pool algo.
    cs_pool2 = calc_chunksize(n_workers, len_iterable)

    real_factor_pool1 = cs_naive / cs_pool1
    real_factor_pool2 = cs_naive / cs_pool2

    return cs_naive, cs_pool1, cs_pool2, real_factor_pool1, real_factor_pool2

上面的函数计算了 Pool 的 chunksize-algorithm 的初始块大小(cs_naive)和第一步块大小(cs_pool1),以及完整的 Pool-algorithm 的块大小(cs_pool2)。此外,它还计算了 real 因子rf_pool1 = cs_naive / cs_pool1和rf_pool2 = cs_naive / cs_pool2,它们告诉我们天真计算的块大小比 Pool 的内部版本大多少倍。

下面您会看到使用此函数的输出创建的两个图形。左图只显示了n_workers=4的块大小,直到500的可迭代长度。右图显示了rf_pool1的值。对于可迭代长度16,实因子变为>=4(对于len_iterable >= n_workers * 4),对于可迭代长度28-31,其最大值为7。这与算法收敛到更长迭代的原始因子4有很大偏差。这里的“更长”是相对的,取决于指定工人的数量。

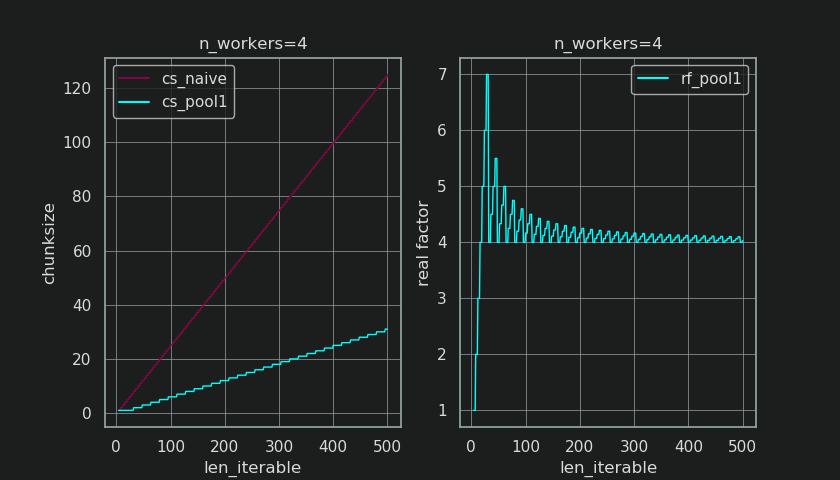
请记住,chunksizecs_pool1仍然缺少extra-调整,而divmod的余数包含在完整算法的cs_pool2中。

算法继续:

if extra:
    chunksize += 1

现在,如果存在余数(来自 divmod 操作的extra),将块大小增加 1 显然不能对每个任务都有效。毕竟,如果可以的话,就没有剩余的开始了。

从下图中可以看出,“额外处理”的效果是,rf_pool2的 real factor 现在从_below_4向4收敛,并且偏差更加平滑。n_workers=4和len_iterable=500的标准差从rf_pool1的0.5233下降到rf_pool2的0.4115。

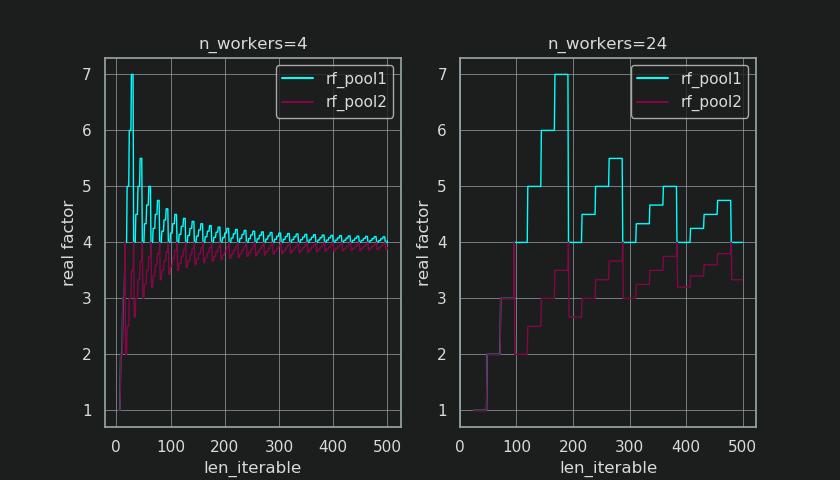
最终,将chunksize增加 1 的效果是,最后传输的任务的大小仅为len_iterable % chunksize or chunksize。

额外处理的效果更有趣以及我们稍后将如何看到,更重要的效果可以观察到生成的块数(n_chunks)。对于足够长的迭代,Pool 完成的 chunksize-algorithm(下图中的n_pool2)会将 chunk 的数量稳定在n_chunks == n_workers * 4。相比之下,朴素算法(在初始打嗝之后)随着迭代长度的增长在n_chunks == n_workers和n_chunks == n_workers + 1之间保持交替。

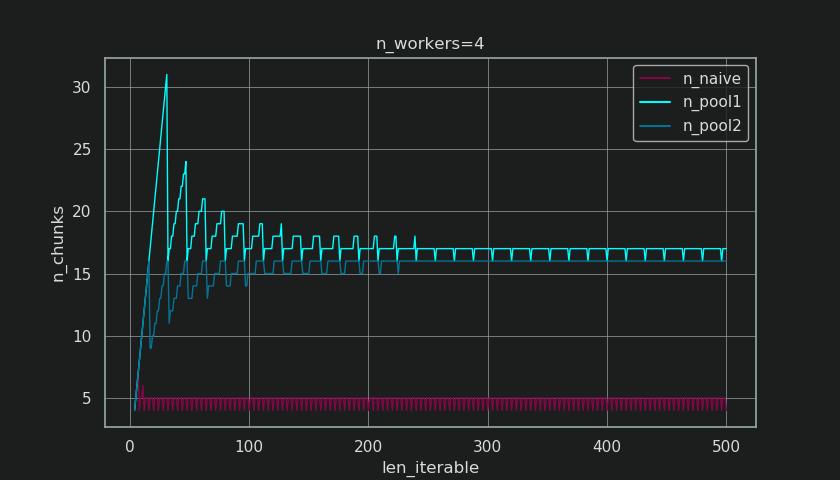
下面你会发现两个增强的信息功能池和天真的块大小算法。下一章将需要这些函数的输出。

# mp_utils.py

from collections import namedtuple


Chunkinfo = namedtuple(
    'Chunkinfo', ['n_workers', 'len_iterable', 'n_chunks',
                  'chunksize', 'last_chunk']
)

def calc_chunksize_info(n_workers, len_iterable, factor=4):
    """Calculate chunksize numbers."""
    chunksize, extra = divmod(len_iterable, n_workers * factor)
    if extra:
        chunksize += 1
    # `+ (len_iterable % chunksize > 0)` exploits that `True == 1`
    n_chunks = len_iterable // chunksize + (len_iterable % chunksize > 0)
    # exploit `0 == False`
    last_chunk = len_iterable % chunksize or chunksize

    return Chunkinfo(
        n_workers, len_iterable, n_chunks, chunksize, last_chunk
    )

不要被calc_naive_chunksize_info可能出乎意料的外观所迷惑。divmod中的extra不用于计算块大小。

def calc_naive_chunksize_info(n_workers, len_iterable):
    """Calculate naive chunksize numbers."""
    chunksize, extra = divmod(len_iterable, n_workers)
    if chunksize == 0:
        chunksize = 1
        n_chunks = extra
        last_chunk = chunksize
    else:
        n_chunks = len_iterable // chunksize + (len_iterable % chunksize > 0)
        last_chunk = len_iterable % chunksize or chunksize

    return Chunkinfo(
        n_workers, len_iterable, n_chunks, chunksize, last_chunk
    )

---

6.量化算法效率

现在,在我们看到Pool的块大小算法的输出与朴素算法的输出相比看起来有何不同之后......

• 如何判断 Pool 的方法是否真的_改进_了一些东西?

• 这_something_到底是什么?

如上一章所示,对于更长的可迭代对象(更大数量的任务),Pool 的 chunksize-algorithm approximately 将可迭代对象划分为比 naive 方法多 4 倍的块。更小的块意味着更多的任务,更多的任务意味着更多的并行化开销(PO),必须权衡增加调度灵活性的好处(回忆**“块大小> 1”的风险**)。

由于相当明显的原因,Pool 的基本块大小算法无法为我们权衡调度灵活性与 PO。 IPC 开销取决于操作系统、硬件和数据大小。该算法不知道我们在什么硬件上运行我们的代码,也不知道任务需要多长时间才能完成。这是一种为_所有_可能的场景提供基本功能的启发式方法。这意味着它无法针对任何特定场景进行优化。如前所述,随着每个任务的计算时间增加(负相关),PO 也变得越来越不受关注。

当您回想起第 2 章中的并行化目标时,其中一个要点是:

• 所有 cpu 核心的高利用率

前面提到的_something_,Pool的chunksize-algorithm_can_尝试改进的是最小化idling worker-processes,分别是利用cpu-cores。

一个关于multiprocessing.Pool的重复问题是人们想知道在您期望所有工作进程都忙的情况下未使用的内核/空闲工作进程的问题。虽然这可能有很多原因,但在计算结束时空闲的工作进程是我们经常可以观察到的,即使在 密集场景(每个任务的计算时间相等)的情况下,工作人员的数量不是除数块数(n_chunks % n_workers > 0)。

现在的问题是:

我们如何才能将我们对块大小的理解转化为能够解释观察到的工人利用率的东西,甚至在这方面比较不同算法的效率?

---

6.1 型号

为了在这里获得更深入的见解,我们需要一种并行计算的抽象形式,它将过于复杂的现实简化到可管理的复杂程度,同时在定义的边界内保持重要性。这样的抽象称为_model_。如果要收集数据,这种“并行化模型”(PM) 的实现会像实际计算一样生成工作映射元数据(时间戳)。模型生成的元数据允许在某些约束下预测并行计算的指标。

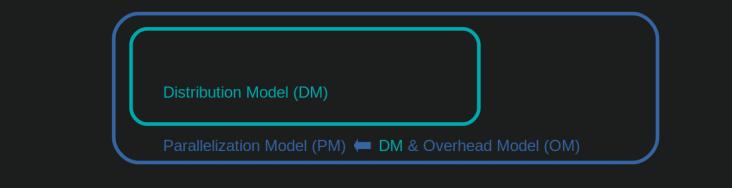
此处定义的PM 中的两个子模型之一是分布模型 (DM)。 DM 解释了原子工作单元(taskels)如何分布在 parallel workers 和 time 上,除了相应的 chunksize-algorithm、worker 数量、input-iterable( taskels) 并考虑了它们的计算持续时间。这意味着_不_包括任何形式的开销。

为了获得完整的 PM,DM 扩展了 Overhead Model (OM),代表各种形式的Parallelization Overhead (PO)。这样的模型需要为每个节点单独校准(硬件、操作系统依赖)。 OM 中表示多少形式的开销是开放的,因此可以存在具有不同复杂程度的多个 OM。实现的 OM 需要的准确度级别取决于特定计算的 PO 的总体权重。更短的任务导致 PO 的权重更高,如果我们试图_预测_并行化效率 (PE),这反过来又需要更精确的 OM。

---

6.2 并行调度(PS)

Parallel Schedule 是并行计算的二维表示,其中 x 轴代表时间,y 轴代表并行工作池。工作人员的数量和总计算时间标志着一个矩形的延伸,其中绘制了较小的矩形。这些较小的矩形代表原子工作单元(taskels)。

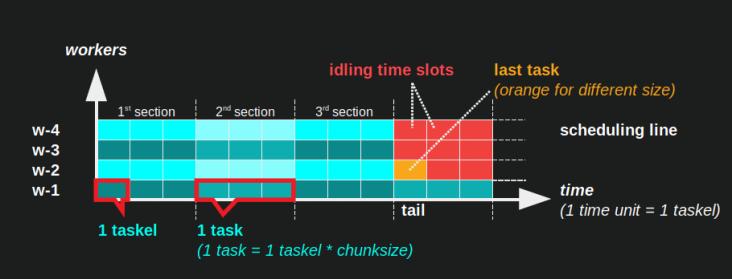
下面是 PS 的可视化,它使用来自 Dense Scenario 的 Pool 的 chunksize-algorithm 的 DM 的数据。

• x 轴被划分为相等的时间单位,其中每个单位代表 taskel 所需的计算时间。

• y 轴分为池使用的工作进程数。

• 这里的taskel显示为最小的青色矩形,放入匿名工作进程的时间线(时间表)中。

• 任务是工作时间线中的一个或多个任务,以相同的色调连续突出显示。

• 空闲时间单位通过红色瓷砖表示。

• 并行调度被划分为多个部分。最后一部分是尾部。

组成部分的名称如下图所示。

在包含 OM 的完整 PM 中,Idling Share 不仅限于尾部,还包括任务之间甚至任务之间的空间。

---

6.3 效率

上面介绍的模型允许量化工人利用率。我们可以区分:

• 分配效率 (DE) - 在 DM 的帮助下计算(或 Dense Scenario 的简化方法)。

• 并行化效率 (PE) - 借助校准的 PM(预测)计算或根据实际计算的元数据计算。

需要注意的是,计算出的效率**do not** 自动与给定并行化问题的_faster_ 整体计算相关联。在这种情况下,工人利用率仅区分具有已开始但未完成的任务的工人和没有这种“开放”任务的工人。这意味着,可能闲置_during_一个taskel的时间跨度_not_注册。

上述所有效率基本上都是通过计算除法Busy Share / Parallel Schedule的商获得的。 DE 和 PE 之间的区别在于,对于开销扩展的 PM,Busy Share 占据了整个并行计划的较小部分。

该答案将进一步仅讨论为密集场景计算 DE 的简单方法。这足以比较不同的块大小算法,因为......

1. ... DM 是 PM 的一部分,它随着所采用的不同块大小算法而变化。

2. ...每个任务的计算持续时间相等的密集场景描绘了一个“稳定状态”,对于这种状态,这些时间跨度从等式中消失。任何其他情况只会导致随机结果,因为任务的顺序很重要。

---

6.3.1 绝对分配效率(ADE)

这种基本效率通常可以通过将 Busy Share 除以 Parallel Schedule 的全部潜力来计算:

绝对分配效率 (ADE) u003d Busy Share / Parallel Schedule

对于 Dense Scenario,简化的计算代码如下所示:

# mp_utils.py

def calc_ade(n_workers, len_iterable, n_chunks, chunksize, last_chunk):
    """Calculate Absolute Distribution Efficiency (ADE).

    `len_iterable` is not used, but contained to keep a consistent signature
    with `calc_rde`.
    """
    if n_workers == 1:
        return 1

    potential = (
        ((n_chunks // n_workers + (n_chunks % n_workers > 1)) * chunksize)
        + (n_chunks % n_workers == 1) * last_chunk
    ) * n_workers

    n_full_chunks = n_chunks - (chunksize > last_chunk)
    taskels_in_regular_chunks = n_full_chunks * chunksize
    real = taskels_in_regular_chunks + (chunksize > last_chunk) * last_chunk
    ade = real / potential

    return ade

如果没有 Idle Share,Busy Share 将 equal 到 Parallel Schedule,因此我们得到 100% 的 ADE。在我们的简化模型中,这是一个所有可用进程在处理所有任务所需的全部时间内都处于忙碌状态的场景。换句话说,整个作业被有效地并行化到 100%。

但是为什么我在这里一直将 PE 称为 absolute PE 呢?

为了理解这一点,我们必须考虑块大小(cs)的可能情况,以确保最大的调度灵活性(还有可能存在的 Highlander 的数量。巧合?):

________________________\ __________~ 一个~____________ ______________________

例如,如果我们有 4 个工作进程和 37 个任务,即使使用chunksize=1,也会有空闲的工作人员,因为n_workers=4不是 37 的除数。除以 37 / 4 的余数是 1。这个剩余的单个任务将有由一名工人处理,其余三人闲置。

同样,仍然会有一名闲置的工人有 39 个任务,如下图所示。

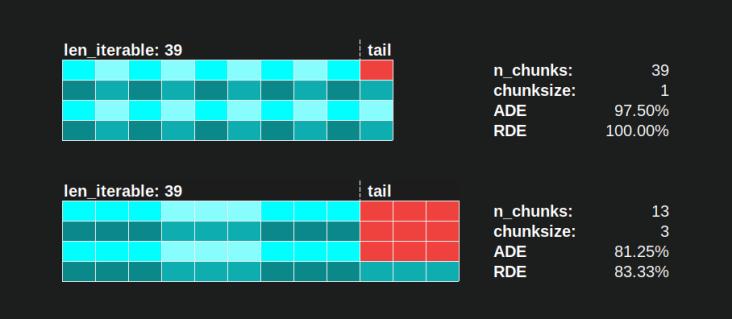
当您将chunksize=1的上 Parallel Schedule 与chunksize=3的以下版本进行比较时,您会注意到上 Parallel Schedule 更小,x 轴上的时间线更短。现在应该很明显了,即使对于密集场景,更大的块大小也会意外地_can_导致整体计算时间增加。

但是为什么不直接使用 x 轴的长度来计算效率呢?

因为此模型中不包含开销。两种块大小都会有所不同,因此 x 轴并不是真正可直接比较的。开销仍然会导致更长的总计算时间,如下图的案例 2 所示。

---

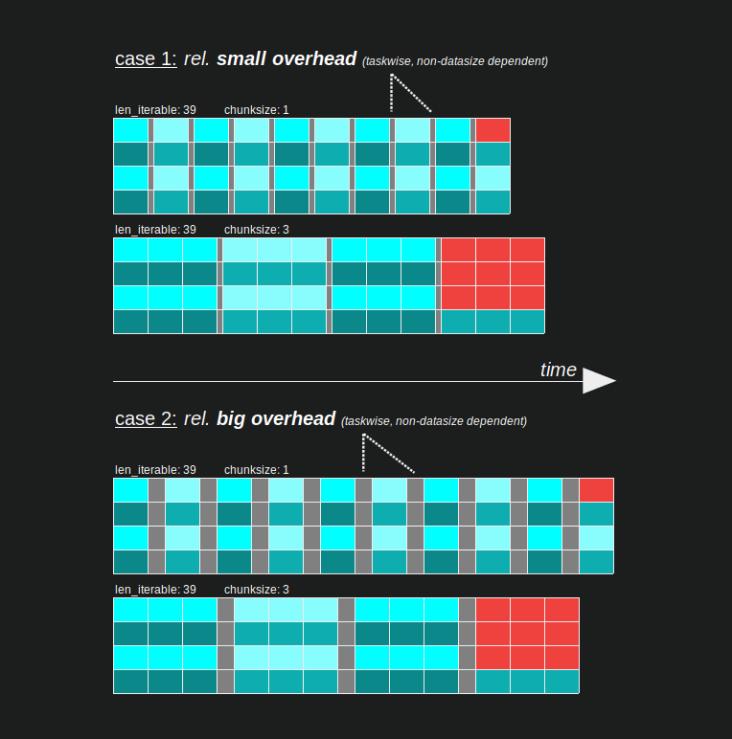
6.3.2 相对分配效率(RDE)

ADE 值不包含是否可以在 chunksize 设置为 1 的情况下 better 分配 taskels 的信息。这里的 Better 仍然意味着较小的 Idling Share。

为了获得针对最大可能 DE 调整的 DE 值,我们必须将考虑的 ADE 除以我们为chunksize=1获得的 ADE。

相对分配效率 (RDE) u003d ADE_cs_x / ADE_cs_1

这是它在代码中的样子:

# mp_utils.py

def calc_rde(n_workers, len_iterable, n_chunks, chunksize, last_chunk):
    """Calculate Relative Distribution Efficiency (RDE)."""
    ade_cs1 = calc_ade(
        n_workers, len_iterable, n_chunks=len_iterable,
        chunksize=1, last_chunk=1
    )
    ade = calc_ade(n_workers, len_iterable, n_chunks, chunksize, last_chunk)
    rde = ade / ade_cs1

    return rde

RDE,这里如何定义,本质上是一个关于 Parallel Schedule 尾部的故事。 RDE 受尾部中包含的最大有效块大小的影响。 (这条尾巴可以是 x 轴长度chunksize或last_chunk。)这会导致 RDE 对于各种“tail-looks”自然收敛到 100%(偶数),如下图所示。

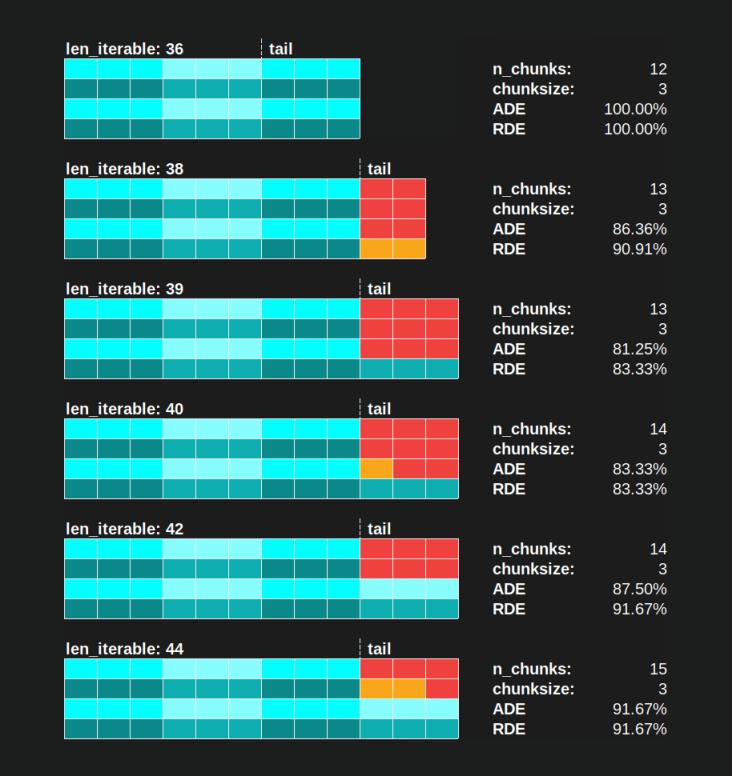
低 RDE ...

• 是优化潜力的有力提示。

• 对于更长的迭代自然变得不太可能,因为整个 Parallel Schedule 的相对尾部缩小了。

---

请在此处找到此答案的第二部分。