I'm trying to get python to return, as close as possible, the center of the most obvious clustering in an image like the one below:

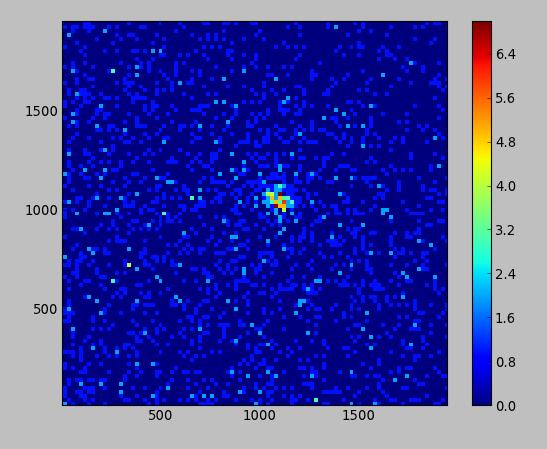
In my previous question I asked how to get the global maximum and the local maximums of a 2d array, and the answers given worked perfectly. The issue is that the center estimation I can get by averaging the global maximum obtained with different bin sizes is always slightly off than the one I would set by eye, because I'm only accounting for the biggest bin instead of a group of biggest bins (like one does by eye).

I tried adapting the answer to this question to my problem, but it turns out my image is too noisy for that algorithm to work. Here's my code implementing that answer:

import numpy as np
from scipy.ndimage.filters import maximum_filter
from scipy.ndimage.morphology import generate_binary_structure, binary_erosion
import matplotlib.pyplot as pp

from os import getcwd
from os.path import join, realpath, dirname

# Save path to dir where this code exists.
mypath = realpath(join(getcwd(), dirname(__file__)))
myfile = 'data_file.dat'

x, y = np.loadtxt(join(mypath,myfile), usecols=(1, 2), unpack=True)
xmin, xmax = min(x), max(x)
ymin, ymax = min(y), max(y)

rang = [[xmin, xmax], [ymin, ymax]]
paws = []

for d_b in range(25, 110, 25):
    # Number of bins in x,y given the bin width 'd_b'
    binsxy = [int((xmax - xmin) / d_b), int((ymax - ymin) / d_b)]

    H, xedges, yedges = np.histogram2d(x, y, range=rang, bins=binsxy)
    paws.append(H)


def detect_peaks(image):
    """
    Takes an image and detect the peaks usingthe local maximum filter.
    Returns a boolean mask of the peaks (i.e. 1 when
    the pixel's value is the neighborhood maximum, 0 otherwise)
    """

    # define an 8-connected neighborhood
    neighborhood = generate_binary_structure(2,2)

    #apply the local maximum filter; all pixel of maximal value 
    #in their neighborhood are set to 1
    local_max = maximum_filter(image, footprint=neighborhood)==image
    #local_max is a mask that contains the peaks we are 
    #looking for, but also the background.
    #In order to isolate the peaks we must remove the background from the mask.

    #we create the mask of the background
    background = (image==0)

    #a little technicality: we must erode the background in order to 
    #successfully subtract it form local_max, otherwise a line will 
    #appear along the background border (artifact of the local maximum filter)
    eroded_background = binary_erosion(background, structure=neighborhood, border_value=1)

    #we obtain the final mask, containing only peaks, 
    #by removing the background from the local_max mask
    detected_peaks = local_max - eroded_background

    return detected_peaks


#applying the detection and plotting results
for i, paw in enumerate(paws):
    detected_peaks = detect_peaks(paw)
    pp.subplot(4,2,(2*i+1))
    pp.imshow(paw)
    pp.subplot(4,2,(2*i+2) )
    pp.imshow(detected_peaks)

pp.show()

and here's the result of that (varying the bin size):

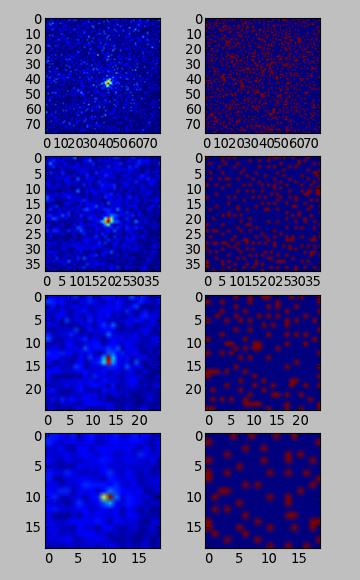
Clearly my background is too noisy for that algorithm to work, so the question is: how can I make that algorithm less sensitive? If an alternative solution exists then please let me know.

---

EDIT

Following Bi Rico advise I attempted smoothing my 2d array before passing it on to the local maximum finder, like so:

H, xedges, yedges = np.histogram2d(x, y, range=rang, bins=binsxy)
H1 = gaussian_filter(H, 2, mode='nearest')
paws.append(H1)

These were the results with a sigma of 2, 4 and 8:

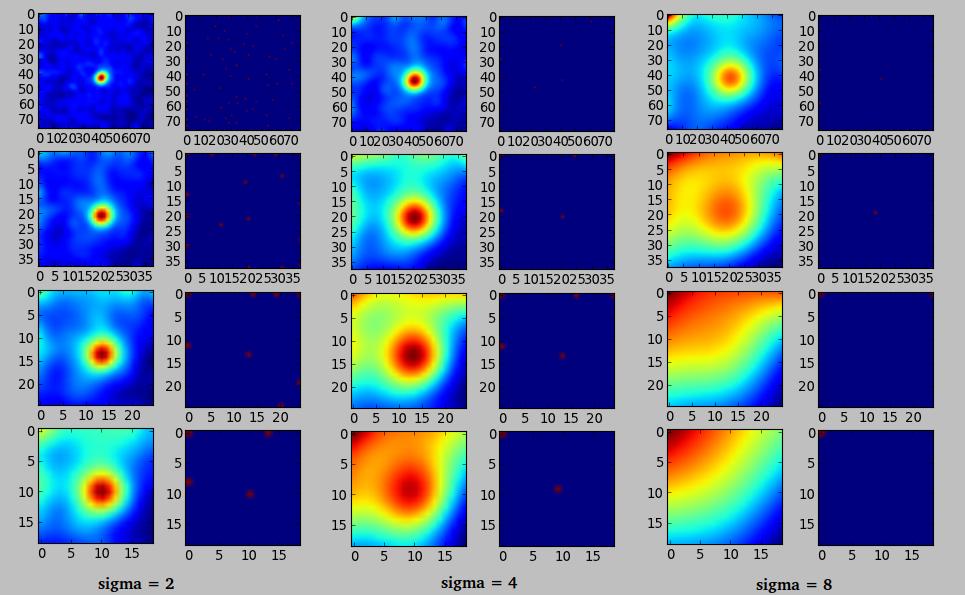
EDIT 2

A mode ='constant' seems to work much better than nearest. It converges to the right center with a sigma=2 for the largest bin size:

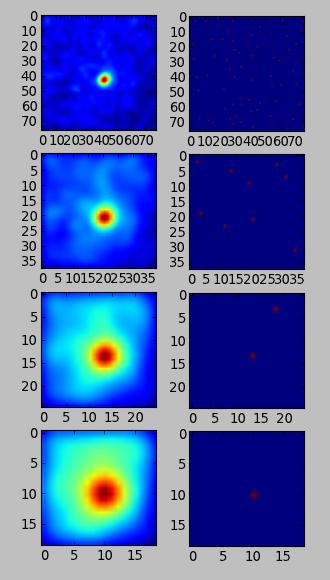
So, how do I get the coordinates of the maximum that shows in the last image?

I'm adding this answer because it's the solution I ended up using. It's a combination of Bi Rico's comment here (May 30 at 18:54) and the answer given in this question: Find peak of 2d histogram.

As it turns out using the peak detection algorithm from this question Peak detection in a 2D array only complicates matters. After applying the Gaussian filter to the image all that needs to be done is to ask for the maximum bin (as Bi Rico pointed out) and then obtain the maximum in coordinates.

So instead of using the detect-peaks function as I did above, I simply add the following code after the Gaussian 2D histogram is obtained:

# Get 2D histogram.
H, xedges, yedges = np.histogram2d(x, y, range=rang, bins=binsxy)
# Get Gaussian filtered 2D histogram.
H1 = gaussian_filter(H, 2, mode='nearest')
# Get center of maximum in bin coordinates.
x_cent_bin, y_cent_bin = np.unravel_index(H1.argmax(), H1.shape)
# Get center in x,y coordinates.
x_cent_coor , y_cent_coord = np.average(xedges[x_cent_bin:x_cent_bin + 2]), np.average(yedges[y_cent_g:y_cent_g + 2])