神经元

深度学习中最基本的概念:神经元,流行的神经网络,几乎是由不同方式组合的神经元组成。一个完整的神经元主要由线性函数和激励函数两部分组成。

线性函数:

y u003d wX + b

线性函数的公式就是这样表示的,其中x代表输入,y代表输出,w代表权重,b代表偏差。

input:神经元处理前的数据,x不一定是数字,也可以是矩阵或其他数据

输出:神经元处理的数据。输出数据也可以是各种形式的数据,由输入数据和神经元决定

权重:进入神经元时相乘的数据可以是数字也可以是矩阵。通常,初始权重是随机设置的。训练结束后,计算机会调整权重,对比较重要的特征赋予较大的权重,反之,对不重要的特征赋予较小的权重。

偏差:输入和权重相乘的结果加上线性分量,可以增加线性范围

激活函数(激发函数):

激活函数就是给神经元添加非线性因子。因为线性函数所能表达的内容有很大的局限性,现实中很多问题都是非线性的,所以加入非线性因素可以增加模型的拟合效果。

常见的激活函数:

常用的激活函数包括sigmoid函数、relu函数、tanh函数、softmax函数等。

sigmoid函数:

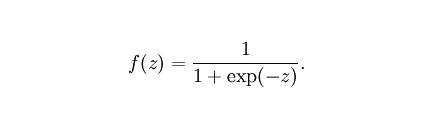
,也称为逻辑函数,用于隐藏层神经元输出。取值范围为 (0,1)。它可以将一个实数映射到(0,1)的区间,可以用于二分类。在特征差异比较复杂或者差异不是特别大的情况下效果更好。

sigmoid缺点:激活函数计算量大。通过反向传播计算误差梯度时,推导涉及除法。在反向传播过程中,梯度很容易消失,因此无法完成深度网络的训练。

为什么梯度会消失:在反向传播算法中,需要推导激活函数。 sigmoid的导数表达式为:

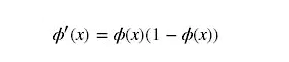
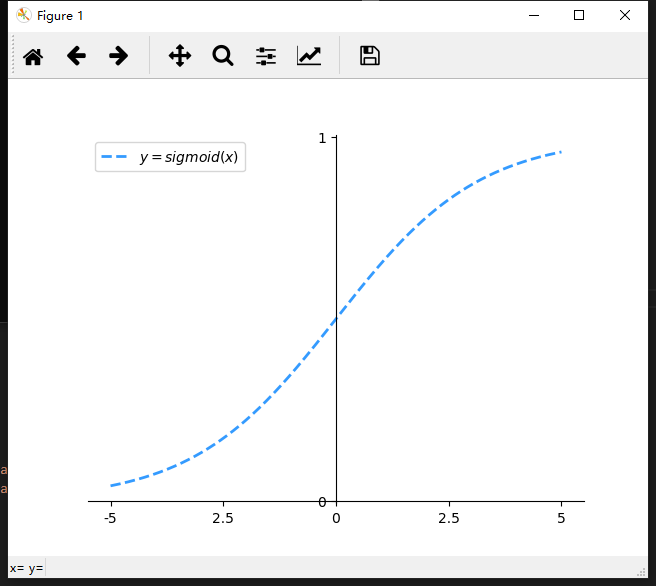
sigmoid原函数和导数图如下:从图中可以看出导数从0快速逼近0,容易造成“梯度消失”现象

绘制 sigmoid 函数:

"""

画一条直线 sigmoid 曲线

"""

将 numpy 导入为 np

导入 matplotlib.pyplot 作为 mp

导入数学

def sigmoid(x):

y u003d 1 / (1 + np.exp(-x))

返回 y

[- π, π] 拆1000分

x u003d np.linspace(-np.pi, np.pi, 1000)

sigmoid_x u003d sigmoid(x)

映射

mp.plot(x, sigmoid_x, linestyleu003d'--', linewidthu003d2,

颜色u003d'dodgerblue', alphau003d0.9,

标签u003dr'$yu003dsigmoid(x)$')

修改坐标比例

x_val_listu003d[-np.pi, -np.pi/2, 0, np.pi/2, np.pi]

x_text_listu003d['-5', '2.5', '0', '2.5', '5']

mp.xticks(x_val\list, ax\text\list)

mp.yticks([0, 1],

['0', '1'])

设置轴

斧头 u003d mp.gca()

ax.spines['top'].set_color('none')

ax.spines['right'].set_color('none')

ax.spines['left'].set_position(('data',0))

ax.spines['bottom'].set_position(('data',0))

显示图例

mp.legend(locu003d'best')

mp.show()

重新功能:

绘制relu函数:

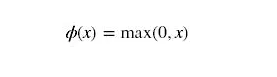
ReLU的优点:用ReLU得到的SGD的收敛速度比sigmoid/tanh快很多

ReLU的缺点:训练时非常“脆弱”,很容易“死”。例如,一个非常大的梯度流经一个 ReLU 神经元。更新参数后,神经元将不再激活任何数据,因此神经元的梯度永远为0。如果学习率大,很可能网络中40%的神经元都“死”了。

"""

画relu

"""

将 numpy 导入为 np

导入 matplotlib.pyplot 作为 mp

导入数学

定义 Relu(x):

y u003d []

对于 x 中的 xx:

如果 xx >u003d 0:

y.append(xx)

其他:

y.append(0)

返回 y

[- π, π] 拆1000分

x u003d np.linspace(-np.pi, np.pi, 1000)

重读_x u003d 重读(x)

映射

mp.plot(x, Relu_x, linestyleu003d'--', linewidthu003d2,

颜色u003d'dodgerblue', alphau003d0.9,

标签u003dr'$yu003drelu(x)$')

修改坐标比例

x_val_listu003d[-np.pi, -np.pi/2, 0, np.pi/2, np.pi]

x_text_listu003d['-π', r'$-\frac{\pi}{2}$', '0',

r'$\frac{π}{2}$', 'π']

mp.xticks(x_val\list, ax\text\list)

mp.yticks([-1, -0.5, 0.5, 1],

['-1', '-0.5', '0.5', '1'])

设置轴

斧头 u003d mp.gca()

ax.spines['top'].set_color('none')

ax.spines['right'].set_color('none')

ax.spines['left'].set_position(('data',0))

ax.spines['bottom'].set_position(('data',0))

显示图例

mp.legend(locu003d'best')

mp.show()

tanh 函数

绘制tanh函数:

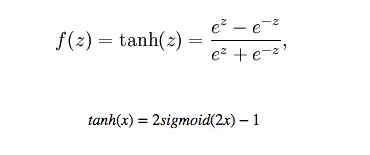
8195. 当特征差异明显时,tanh的效果会非常好,并且特征效果会在流通过程中不断扩大。 tanh和sigmoid的区别在于tanh是零均值,所以在实际应用中tanh会比sigmoid好

"""

绘制一条直线 tanh 曲线

"""

将 numpy 导入为 np

导入 matplotlib.pyplot 作为 mp

[- π, π] 拆1000分

x u003d np.linspace(-np.pi, np.pi, 1000)

tanh_x u003d np.tanh(x)

映射

mp.plot(x, tanh_x, linestyleu003d'--', linewidthu003d2,

颜色u003d'dodgerblue', alphau003d0.9,

标签u003dr'$yu003dtanh(x)$')

修改坐标比例

x_val_listu003d[-np.pi, -np.pi/2, 0, np.pi/2, np.pi]

x_text_listu003d['-π', r'$-\frac{\pi}{2}$', '0',

r'$\frac{π}{2}$', 'π']

mp.xticks(x_val\list, ax\text\list)

mp.yticks([-1, -0.5, 0.5, 1],

['-1', '-0.5', '0.5', '1'])

设置轴

斧头 u003d mp.gca()

ax.spines['top'].set_color('none')

ax.spines['right'].set_color('none')

ax.spines['left'].set_position(('data',0))

ax.spines['bottom'].set_position(('data',0))

显示图例

mp.legend(locu003d'best')

mp.show()

softmax 函数

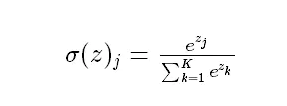
通过激活函数将输出层的值映射到0-1区间,将神经元输出构造成多分类问题的概率分布。 softmax激活函数的映射值越大,真实类别的可能性就越大。

sigmoid一般用于二分类问题,而softmax用于多分类问题

参考:

链接:https://www.jianshu.com/p/22d9720dbf1a