Python位运算符——详解

• Python位操作根据内存中数据的二进制位(bits)进行操作。一般用于底层开发(算法设计、驱动、图像处理、单片机等),在应用层开发(Web开发、Linux运维等)中并不常见。想要加快学习速度或者不关注底层开发的读者可以先跳过这一部分,以后有需要的时候再学习。

Python 位运算符只能用于操作整数类型。它们是根据内存中整数的二进制形式计算的。 Python支持的位运算符如表1所示。

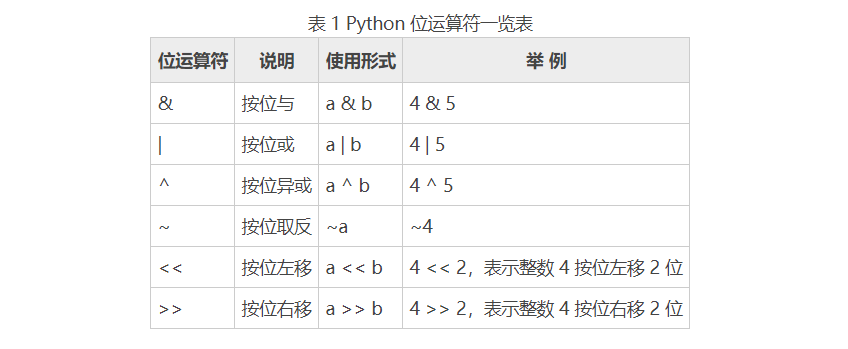
&位与运算符

• 按位与运算符&的运算规则是:只有&运算涉及的两位为1时结果为1,否则为0。例如1&1为1,0&0为0 , 1 & 0 为 0,与逻辑运算符 & & 非常相似。

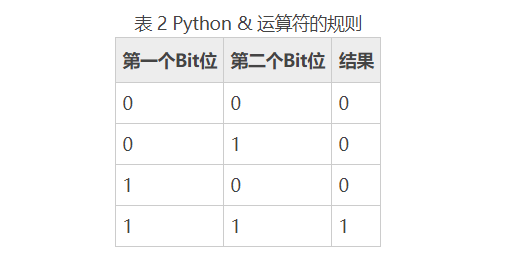
例如 9&5 可以转化为如下运算:

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1001 (9 存储在内存中)

& 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0101 (5 存储在内存中)

---

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0001 (1 存储在内存中)

运算符将对运算中涉及的两个整数的所有二进制位进行&运算,9&5的结果为1。

再举一个例子,-9&5 可以转换成以下操作:

1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0111 (-9 存储在内存中)

& 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0101 (5 存储在内存中)

---

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0101 (5 存储在内存中)

-9-5 的结果是 5。

同样,& 运算符对存储在内存中的数据的原始二进制位进行操作,而不是数据本身的二进制形式;其他位运算符也是如此。

以 - 9 & 5 为例, - 9 在内存中的存储与 - 9 的二进制形式有很大不同:

1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0111 (-9 存储在内存中)

-0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1001 (-9二进制形式,前面多余的0可以擦掉)

按位和运算通常用于将某些位清 0 或保留某些位。例如,要将n的高16位清0,保留低16位,可以进行n&0xfff操作(0xfff在内存中的存储形式为0000 0000 – 0000 0000 – 1111 1111 1111)。

用 Python 代码验证上述分析:

n u003d 0X8FA6002D

打印("%X" % (9&5) )

打印("%X" % (-9&5) )

打印("%X" % (n&0XFFFF) )

运行结果:

1

5

可能

|按位或运算符

• 按位或运算符的运算规则 |即:当两个二进制位中的一个为1时,结果为1,同时为0时,结果为0。例如,1 | 1 是 1, 0 | 0 是 0,而 1 | 0 是 1,与 | 非常相似在逻辑运算中。

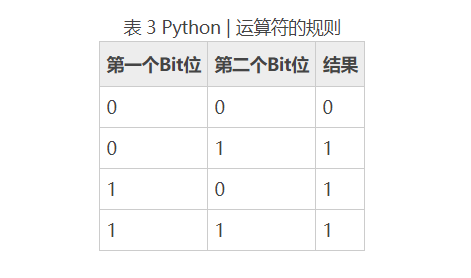
例如,9 | 5 可转化为以下运算:

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1001 (9 存储在内存中)

| 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0101 (5 存储在内存中)

---

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1101 (13 存储在内存中)

9 的结果 | 5 是 13。

再举一个例子,- 9 | 5 可转化为以下运算:

1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0111 (-9 存储在内存中)

| 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0101 (5 存储在内存中)

---

1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0111 (-9 存储在内存中)

-9 的结果 | 5 是 - 9。

按位或运算可用于将某些位置设置为 1,或保留某些位。例如,如果要保留 N 的高 16 位 1 和低 16 位,可以执行 n | 0xfff0000操作(0xfff0000在内存中的存储形式为1111 1111 – 1111 1111 – 0000 0000 – 0000)。

用 Python 代码验证上述分析:

n u003d 0X2D

打印("%X" % (9|5) )

打印("%X" % (-9|5) )

打印("%X" % (n|0XFFFF0000) )

运行结果:

D

-9

FFFF002D

^按位异或运算符

• 按位异或运算^的运算规则是:运算所涉及的两个二进制位如果不同则结果为1,如果相同则结果为0。例如0^1为1、0 ^ 0 为 0, 1 ^ 1 为 0。

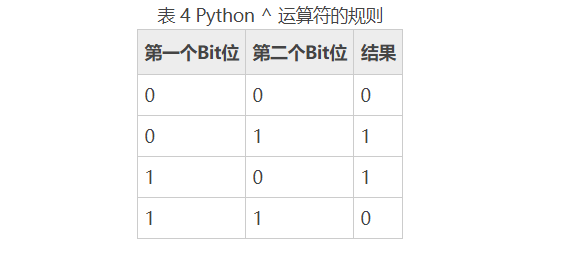
例如,9 ^ 5 可以转换为以下运算:

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1001 (9 存储在内存中)

^ 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0101 (5 存储在内存中)

---

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1100 (12 存储在内存中)

9 ^ 5 的结果是 12。

再举一个例子,-9 ^ 5 可以转换成如下运算:

1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0111 (-9 存储在内存中)

^ 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0101 (5 存储在内存中)

---

1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0010 (-14 存储在内存中)

-9 ^ 5 的结果是 - 14。

按位异或可用于反转某些二进制位。例如,要反转N的高16位,保留低16位,可以进行n^0xfff0000操作(0xfff0000在内存中的存储形式为1111 1111 – 1111 1111 – 0000 0000 – 0000 0000)。

用 Python 代码验证上述分析:

n u003d 0X0A07002D

打印("%X" % (9^5) )

打印("%X" % (-9^5) )

打印("%X" % (n^0XFFFF0000) )

运行结果:

C

-E

F5F8002D

~按位否定运算符

• 按位取反运算符是一元运算符(只有一个操作数),是右结合的。它用于取反操作中涉及的二进制位。比如1是0,~0是1,和逻辑运算是一样的!非常相似。

例如,~9 可以转换为以下操作:

~ 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1001 (9 存储在内存中)

---

1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0110 (-10 存储在内存中)

所以 ~9 的结果是 - 10。

例如,~-9 可以转换为以下操作:

~ 1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0111 (-9 存储在内存中)

---

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1000 (8 存储在内存中)

所以 ~-9 的结果是 8。

用 Python 代码验证上述分析:

打印("%X" % (~9) )

打印("%X" % (~-9) )

运行结果:

-A

8

< < 左移运算符

• Python左移运算符<<用于将操作数的所有二进制位左移几位,丢弃高位,用0填充低位。

例如,9 < < 3 可以转换为以下操作:

<< 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1001 (9 存储在内存中)

---

0000 0000 -- 0000 0000 -- 0000 0000 -- 0100 1000 (72 存储在内存中)

所以 9 < < 3 的结果是 72。

再举一个例子,(- 9) < < 3 可以转化为以下运算:

<< 1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0111 (-9 存储在内存中)

---

1111 1111 -- 1111 1111 -- 1111 1111 -- 1011 1000 (-72 存储在内存中)

所以 (- 9) < < 3 结果为 - 72

如果数据很小,丢弃的高位不包含1,则左移n位相当于乘以2的n次方。

用 Python 代码验证上述分析:

打印("%X" % (9<<3) )

打印("%X" % ((-9)<<3) )

运行结果:

48

-48

>>右移运算符

• Python右移运算符>>用于将操作数的所有二进制位右移几位,丢弃低位,用0或1填充高位。如果数据的最高位为0,则填充在 0;如果最高阶为1,则补1。

例如,9 > > 3 可以转换为以下操作:

>> 0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 1001 (9 存储在内存中)

---

0000 0000 -- 0000 0000 -- 0000 0000 -- 0000 0001 (1 存储在内存中)

所以 9 > > 3 的结果是 1。

再举一个例子,(- 9) > > 3 可以转换为以下操作:

>> 1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 0111 (-9 存储在内存中)

---

1111 1111 -- 1111 1111 -- 1111 1111 -- 1111 1110 (-2 存储在内存中)

所以 (- 9) > > 3 的结果是 - 2

如果丢弃的低位不包含 1,则右移 n 位相当于除以 2 的 n 次方(但移除的位通常包含 1)。

用 Python 代码验证上述分析:

打印("%X" % (9>>3) )

打印("%X" % ((-9)>>3) )

运行结果:

1

-2