时间序列分析——23 DTW(时间序列相似度测量算法)

DTW初探

简介

在时间序列分析中,DTW(Dynamic Time Warping)是一种用于检测两个时间序列相似度的算法,通常用距离来表示。例如以下两个序列,

a u003d [ 1 , 2 , 3 ] au003d[1,2,3] au003d[1,2,3]

b u003d [ 3 , 2 , 2 ] bu003d[3,2,2] bu003d[3,2,2]

我们如何测量两个序列之间的距离?一个明显的方法是,将两个序列中的元素根据它们的位置一个一个地计算距离,最后相加或相加后求平均。这听起来是一种相对简单易懂的方法。我们可以观察下图来理解时间相似度的度量。

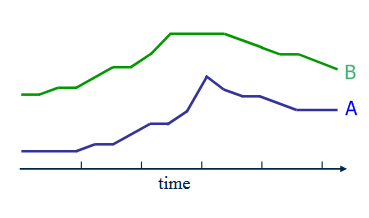
但如果是下面的顺序,

a u003d [ 1 , 2 , 3 ] au003d[1,2,3] au003d[1,2,3]

b u003d [ 2 , 2 , 2 , 3 , 4 ] bu003d[2,2,2,3,4] bu003d[2,2,2,3,4]

我们应该做什么?

DTW 是解决此类问题最常用的算法之一。

事实上,这种算法并不能解决两个序列长度不一样的问题,即使序列的长度不一样。

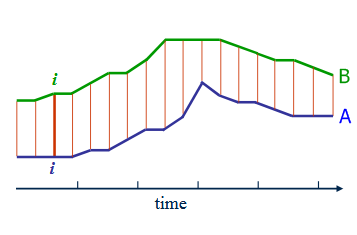
简而言之,DTW算法提供两个序列的弹性比对,找到最佳比对,并根据最佳比对计算距离。

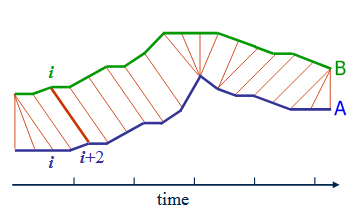
应用程序

DTW 的应用范围非常广泛。例如,它可以用来寻找相似的步行模式,即使一个是快走,另一个是慢走,或者一个是减速或加速。

DTW已应用于视频、音频、图像等多种可序列化数据,如根据音频识别说话人、签名识别等。

另一个典型的应用是股票市场的时间序列分析。在股市中,人们总是希望预测未来,但通用的机器学习算法在这个领域并不是很有效。因为机器学习的预测任务一般要求其训练集和测试集具有相同的维度特征属性。但我们知道,即使一只股票出现了完全相同的形态,其K线和其他指标的反映长度也不相同。

zoz100006 DTW算法规则

DTW就是计算两个序列在一定规则和约束下的最优匹配:

• 第一个序列的每个位置元素必须匹配第二个序列的一个或多个位置元素,反之亦然。

• 第一个序列的第一个元素必须匹配第二个序列的第一个元素,但也可以匹配其他位置。

• 第一个序列的最后一个元素必须匹配第二个序列的最后一个元素,但也可以匹配其他位置。

• 两个序列的位置映射关系一定是单调递增的,反之亦然。比如第一个序列的1,3位置映射到第二个序列的2,3位置是可以的,但是如果映射到3,2位置就不行了。

最优匹配是在上述所有约束条件下损失最小的匹配。最小损失是映射位置上的值的距离之和。综上所述,头部和尾部必须匹配。没有交叉映射,也没有残基子序列。

先来看伪代码:

int DTWDistance(s:数组[1..n],t:数组[1..m]){

DTW :u003d 数组 [0..n, 0..m]

对于 i :u003d 0 到 n

对于 j :u003d 0 到 m

DTW[i, j] :u003d 无穷大

DTW[0, 0] :u003d 0

对于 i :u003d 1 到 n

对于 j :u003d 1 到 m

成本 :u003d d(s[i], t[j])

DTW[i, j] :u003d cost + minimum(DTW[i-1, j ], // 插入

DTW[i , j-1], // 删除

DTW[i-1, j-1]) // 匹配

返回 DTW[n, m]

}

这里,d ( x , y ) u003d ∣ x − y ∣ d(x,y)u003d|x-y| d(x,y) u003d ∣ x − y ∣ 和 D T W [ i , j ] DTW[i,j] DTW[i,j] 表示最佳比对下的序列 s [ 1 : i ] s[1:i] s[1:i] 和 t [ 1 : j ] t[1:j] t[1:j] 之间的距离。

该算法的核心是:

DTW[i, j] :u003d 成本 + 最小值(DTW[i-1, j ], //插入

DTW[i , j-1], //删除

DTW[i-1, j-1]) //匹配

显然,这是一种动态规划算法。两个序列 s [ 1 : i ] s[1:i] s[1:i] 和 t [ 1 : j ] t[1:j] t[1 :j] 是 i i i 和 j j 的距离加上以下三个子问题的最小距离

• 分题1:DTW[i-1,j]理解为s s s序列插入一个点

• 分题2:DTW[i,j-1]理解为t t t序列删除一个点

• 子问题3:DTW[i-1,j-1]理解为最后一个时间点匹配的两个序列

Python代码如下

def dtw(s, t):

n, m u003d len(s), len(t)

dtw_matrix u003d np.zeros((n+1, m+1))

对于范围内的 i (n+1):

对于范围内的 j (m+1):

dtw_matrix[i, j] u003d np.inf

dtw_matrix[0, 0] u003d 0

对于范围内的 i (1, n+1):

对于范围内的 j (1, m+1):

成本 u003d abs(s[i-1] - t[j-1])

从一个方框中取出最后一分钟

最后_min u003d np.min([dtw_matrix[i-1, j], dtw_matrix[i, j-1], dtw_matrix[i-1, j-1\ ]])

dtw_matrix[i, j] u003d 成本 + 最后_min

返回 dtw_matrix

例如

将 numpy 导入为 np

a u003d [1,2,3]

b u003d [2,2,2,3,4]

dtw(a,b)

数组([[ 0., inf, inf, inf, inf, inf],

[inf, 1., 2., 3., 5., 8.],

[inf, 1., 1., 1., 2., 4.],

[inf, 2., 2., 2., 1., 2.]])

最后一个元素的值是两个序列之间的距离,即2。

增加窗口限制

上述算法的一个问题是,允许一个序列中的一个元素匹配另一个元素的元素数量没有限制。在这种情况下,如果其中一个序列太长,就会导致性能问题。例如,

a u003d [ 1 , 2 , 3 ] au003d[1,2,3] au003d[1,2,3]

b u003d [ 1 , 2 , 2 , 2 , 2 , 2 , . . . , 5 ] bu003d[1,2,2,2,2,2,...,5] bu003d[1,2,2,2,2,2,...,5]

为了避免这个问题,我们可以添加一个窗口参数来限制一个时间点在另一个时间点可以匹配的元素数量。

伪代码如下

int DTWDistance(s: 数组 [1..n], t: 数组 [1..m], w: int) {

DTW :u003d 数组 [0..n, 0..m]

w :u003d max(w, abs(n-m)) // 调整窗口大小 (*)

对于 i :u003d 0 到 n

对于 j:u003d 0 到 m

DTW[i, j] :u003d 无穷大

DTW[0, 0] :u003d 0

对于 i :u003d 1 到 n

对于 j :u003d max(1, i-w) 到 min(m, i+w)

DTW[i, j] :u003d 0

对于 i :u003d 1 到 n

对于 j :u003d max(1, i-w) 到 min(m, i+w)

成本 :u003d d(s[i], t[j])

DTW[i, j] :u003d cost + minimum(DTW[i-1, j ], // 插入

DTW[i , j-1], // 删除

DTW[i-1, j-1]) // 匹配

返回 DTW[n, m]

}

Python代码如下

def dtw(s, t, 窗口):

n, m u003d len(s), len(t)

w u003d np.max([窗口,abs(n-m)])

dtw_matrix u003d np.zeros((n+1, m+1))

对于范围内的 i (n+1):

对于范围内的 j (m+1):

dtw_matrix[i, j] u003d np.inf

dtw_matrix[0, 0] u003d 0

对于范围内的 i (1, n+1):

对于范围内的 j (np.max([1, i-w]), np.min([m, i+w])+1):

dtw_matrix[i, j] u003d 0

对于范围内的 i (1, n+1):

对于范围内的 j (np.max([1, i-w]), np.min([m, i+w])+1):

成本 u003d abs(s[i-1] - t[j-1])

从一个方框中取出最后一分钟

最后_min u003d np.min([dtw_matrix[i-1, j], dtw_matrix[i, j-1], dtw_matrix[i-1, j-1\ ]])

dtw_matrix[i, j] u003d 成本 + 最后_min

返回 dtw_matrix

a u003d [1,2,3,3,5]

b u003d [1,2,2,2,2,2,2,4]

dtw(a,b,窗口u003d3)

数组([[ 0., inf, inf, inf, inf, inf, inf, inf, inf],

[inf, 0., 1., 2., 3., inf, inf, inf, inf],

[inf, 1., 0., 0., 0., 0., inf, inf, inf],

[inf, 3., 1., 1., 1., 1., 1., inf, inf],

[inf, 5., 2., 2., 2., 2., 2., 2., inf],

[inf, inf, 5., 5., 5., 5., 5., 5., 3.]])

在窗口参数的控制下,结果为3

Python包

前面的示例代码采用递归实现动态规划。这种方法虽然实现简单,但运行效率很低。所以在实际场景中,一般都会用到一些优化算法,比如

PrunedDTW,SparseDTW,FastDTW和[MultiscaleDTW]zwz100

这里我们使用 FastDTW 来试听

从 fastdtw 导入 fastdtw

从 scipy.spatial.distance 导入欧几里得

x u003d np.array([1, 2, 3, 3, 7])

y u003d np.array([1, 2, 2, 2, 2, 2, 2, 4])

距离,路径 u003d fastdtw(x, y, distu003deuclidean)

打印(距离)

打印(路径)

5.0

[(0, 0), (1, 1), (1, 2), (1, 3), (1, 4), (2, 5), (3, 6), (4, 7 )]

5.0

[(0, 0), (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 7), (3, 7), (4, 7)]

未完待续