纸芯

目标

在这里,作者针对的是 GNN 的图分类问题。研究模型级解释方法。具体方法是训练一个图生成器

使用 f ( . ) f(.) f(.) 表示经过训练的 GNN 模型。 y ∈ c 1 , ⋅ ⋅ ⋅ , c l y \in {c_1,···,c_l} y ∈ c1, ⋅⋅⋅, c l 表示图的标签。给定训练好的 GNN 模型 f ( . ) f(.) f(.) 和标签 c i c_i ci 。图生成器的生成可以预测为 c i c_i ci G ∗ G^* G∗ 的图。定义为

G ∗ u003d a r g m a x G P ( f ( G ) u003d c i ) G^* u003d \mathop{argmax}\limits_{G}P(f(G) u003d c_i) G∗u003dGargmaxP( f(G)u003dci)

即最大化 G ∗ G^* G * 被预测为 c i c_i 的概率。

下图中,四个图被预测为类别3。人类观察到三角图是四个图的共同结构。图生成器的最终目标是生成相似的图并引入图规则(类似于人工验证)以增强有效性。

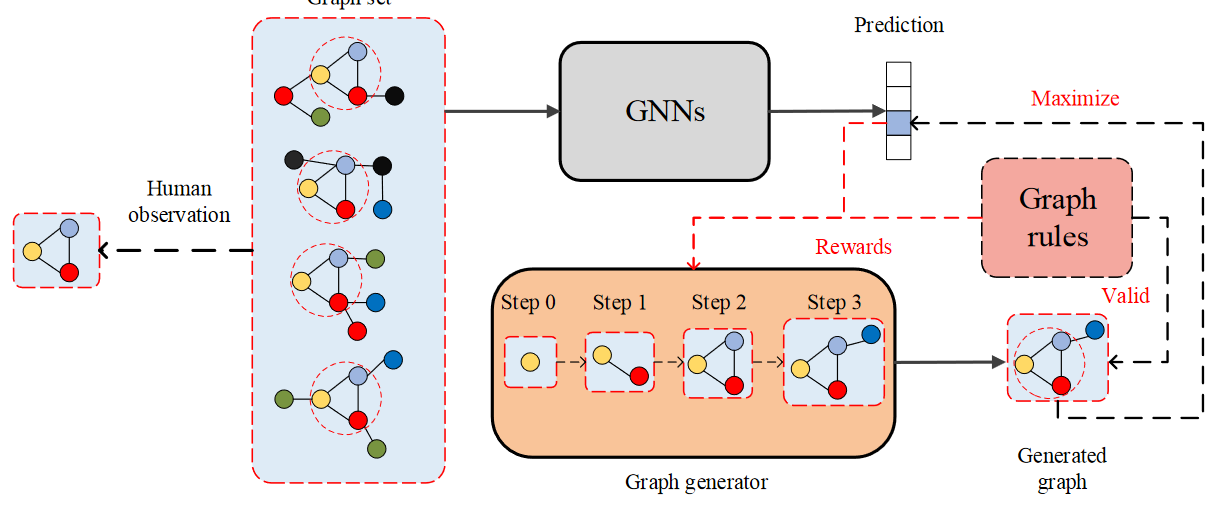
图形生成器目标

将图生成器表示为 g θ ( ⋅ ) g_\theta(·) g θ (⋅)。作者通过 T T T step s 生成 G ∗ G^* G∗。 t t 在时间 t 生成的图是 G t G_t Gt,包括

• n t n_t nt # 个节点

• 特征矩阵 X t ∈ R n t × d X_t \in R^{n_t \times d} Xt∈Rnt×d

• 邻接矩阵 A t ∈ { 0 , 1 } n t × n t A_t \in \{0,1\}^{n_t \times n_t} At∈{0,1}nt ×nt

是

X t + 1 , A t + 1 u003d g θ ( X t , A t ) X_{t+1},A_{t+1} u003d g_\theta(X_t,A\ _t) Xt+1,At+1u003dgθ(Xt,At)

生成任务属于强化学习任务。假设数据集存在 k k k 种节点,定义候选集 C u003d { s 1 , s 2 , ⋅ ⋅ ⋅ , s k } C u003d \{s_1,s_2,···,s_k\} Cu003d{s1,s2,⋅⋅⋅,sk}。比如化学分子图中的节点类型是原子类型,有Cu003d{碳主子,氢主子,·····,氧主子}Cu003d\{碳原子,氢原子,·· ·, 氧原子 \} C u003d {碳原子, 氢原子, ⋅ ⋅, 氧原子}。如果社交网络节点没有分类,则候选集只有一种类型。

g θ ( ⋅ ) g_\theta(·) g θ (⋅) 通过学习如何 G t G_t 将边添加到 Gt G t + 1 G_{t+1} Gt+1。可能包含在 G t G_t 中给 Gt 中的两个节点添加一条边,或者从候选集中添加一个节点。

强化学习任务通常包括四个部分:状态、动作、策略和奖励

• state: t t 时刻t的状态是图G t G_t Gt,初始时刻的图可以由从候选集中随机选择的一个节点组成。也可以手动选择。例如,通常选择碳原子作为生成有机结构图的初始时间。

• Action: t t 时间 t 的动作记录为 a t a_t at。基于图的 G t G_t Gt ^ 生成 G t + 1 G_{t + 1} Gt+1 的过程。具体是选择一个初始节点和一个结束节点,并添加一条边。初始节点 a t , s t a r t a_{t,start} at,start 是 G t G_t Gt 中的节点,结束节点 a t , e n d a_{t,end} at,end ;可以是 G t G\ _t Gt ,或 C C C 中的一个节点。

• Policy:policy是图生成器g θ ( ⋅ ) g_\theta(·) g θ (⋅) 。它可以通过奖励机制和策略梯度来训练。

• 奖励:t t 时间 t 的奖励表示为 R t R_t Rt。它包括 2 个部分:

• 从预训练 GNN f ( . ) f(.) f(.) 引导将增加 g θ ( ⋅ ) g_\theta(·) g θ (⋅) 生成的图被分类为 c i c_i ci的概率。并使用这个概率作为反馈更新 g θ ( ⋅ ) g_\theta(·) gθ(⋅)。

• 提升 g θ ( ⋅ ) g_\theta(·) g θ (⋅) 生成的图在图规则下有效。图规则包括:社交网络中的两个节点不能有多个边,分子图中原子的度数不会超过其化学价。

奖励包括中间奖励和全局奖励。

图形生成器

关于 t t t 时刻,动作 a t a_t at ,记为 ( a t , s t a r t , a t , e n d ) (a_{t,start}, a_{t,end}) (at,start,at,end )。 g θ ( ⋅ ) g_\theta(·) g θ (⋅) 是基于 G t G_t Gt ,和 C C C 来预测不同动作的概率 s p t u003d ( p t , s t a r t , p t , e n d ) p _tu003d(p_{t,start} ,p_{t,end}) ptu003d(pt,start,pt,end)。 g θ ( ⋅ ) g_\theta(·) g θ (⋅) 包含若干个 GCN。

该过程可以描述为

X ^ u003d G C N s ( G t , C ) \widehat{X} u003d GCNs(G_t,C) X u003dGCNs(Gt,C)

p t , s t a r t u003d S o f t m a x ( M L P s ( X ^ ) ) p_{t,start} u003d Softmax(MLPs(\widehat{X})) pt,startu003dSoftmax(MLPs(X ))

p t , e n d u003d S o f t m a x ( M L P s ( [ X ^ , x ^ s t a r t ) ) p_{t,end} u003d Softmax(MLPs([\widehat{X},\hat x_{start })) pt,endu003dSoftmax(MLPs([X ,x^start))

之中

• X ^ \widehat{X} X 为 GCN 学习的节点特征

• a t , s t a r t ∼ p t , s t a r t ⊙ m t , s t a r t a_{t,start} ∼ p_{t,start} \odot m_{t,start} at,start∼pt,start⊙mt ,开始. m t , s t a r t m_{t,start} mt,start 是一个掩码向量,用于过滤掉候选集中的节点, a t , s t a r t a_{t,start} at,start 用于选择 p t , s t a r t p_ {t,start} Pt,start中概率最高的节点

• x ^ s t a r t \hat x_{start} x^start 是一个 t , s t a r t a_{t,start} at,start + 的特征向量

• a t , e n d ∼ p t , e n d ⊙ m t , e n d a_{t,end} ∼ p_{t,end} \odot m_{t,end} at,end∼pt,end⊙mt ,结束。 m t , e n d m_{t,end} mt,end ,是一个掩码向量,用于过滤掉节点 a t , s t a r t a_{t,start} at,start

示例如下图所示。当前图是 G t G_t Gt。可以看到 G t G_t Gt # 包含 4 个节点,候选集有 3 类节点。生成过程包括

• 取 G t G_t Gt X t X_t Xt # 和 C C 的特征矩阵,将 C 中节点的特征向量拼接起来形成特征矩阵 X X X。并将 G t G_t Gt A 的邻接矩阵t A_t At 扩展为 A A A(从 R 4 × 4 R^{4 \times 4} R4 × 4 扩展为 R 7 × 7 R^{7 \times 7} R7×7)

• 每个节点的特征向量通过GCN X ^ \widehat{X} X (青色矩阵)形成

• X ^ \widehat{X} X 通过前MLPs a t , s t a r t a_{t,start} at,start × \times × 预测新添加边的起始节点,该节点为节点掩码ed。可以看到 C C C中的所有节点都被屏蔽了

• X ^ + x ^ s t a r t \widehat{X} + \hat x_{start} X +x^start 通过第二个 MLP a t , e n d a_{t,end} 预测新边的结束节点在,结束。您可以看到起始节点是 mask ed。

• 形成图 G t + 1 G_{t + 1} Gt+1.比 G t G_t Gt # 多了一个节点和一个边。

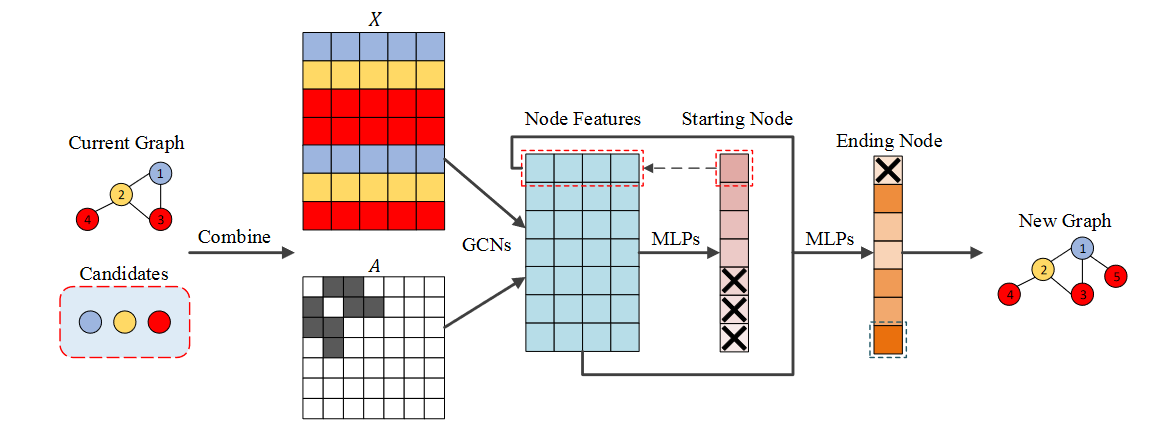
训练图生成器

训练 g θ ( ⋅ ) g_\theta(·) g θ (⋅) 使用策略梯度。公式是

L g u003d - R t ( L C E ( p t , s t a r t , a t , s t a r t ) + L C E ( p t , e n d , a t , e n d ) ) \mathcal{L}_g u003d -R_t(\mathcal{L}\ _{CE}(p_{t,start}, a_{t,start}) + \mathcal{L}_{CE}(p_{t,end}, a_{t ,end})) Lgu003d−Rt(LCE(pt,start,at,start)+LCE(pt,end,at,end))

之中

• L C E \mathcal{L}_{CE} LCE u003d 交叉熵损失

• R t R_t Rt^是t t t时间奖励函数

R t R_t Rt 包括 R t , f R_{t,f} Rt,f ,和 R t , r R_{t,r} Rt,r # 2个部分。

R t , f ( G t + 1 ) u003d p ( f ( G t + 1 ) u003d c i ) − 1 / l R_{t,f}(G_{t+1}) u003d p(f( G_{t+1})u003dci) − 1 / l Rt,f(Gt+1)u003dp(f(Gt+1)u003dci)−1/l

R t , f u003d R t , f ( G t + 1 ) + λ 1 。 ∑ i u003d 0 m R t , f ( R o l l o u t ( G t + 1 ) ) m R_{t,f} u003d R_{t,f}(G_{t+1}) + \ λ_1 。 \frac{\sum_{i u003d 0}^m R_{t,f}(Rollout(G_{t+1}))}{m} Rt,fu003dRt,f (Gt+1)+λ1.m∑iu003d0mRt,f(Rollout(Gt+1))

R t u003d R t , f ( G t + 1 ) + λ 1 。 ∑ 我 u003d 0 米 R t , f ( R o l l o u t ( G t + 1 ) ) m + λ 2 。 R t , r R_t u003d R_{t,f}(G_{t+1}) + \lambda_1 。 \frac{\sum_{i u003d 0}^m R_{t,f}(Rollout(G_{t+1}))}{m} + \lambda_2.R\ _{t,r} Rtu003dRt,f(Gt+1)+λ1.m∑iu003d0mRt,f(Rollout(Gt+1))+λ2.Rt,r

之中

• l l l 为图中的标签个数

• λ 1 \lambda_1 λ 1。而λ 2 \lambda_2 λ 2 ¢是超参数

• R t , r R_{t,r} Rt,r ,代表人工制定的图规则。例如,分子图的每个节点都必须满足化学键的规则(必须是合法的有机物),否则 R t , r R_{t,r} Rt,r ,将为负数

这个算法中最重要的是8、9和10行。

实验

数据集

作者使用合成数据集 Is_Acyclic 和真实数据集 MUTAG。这里我使用MUTAG进行复现。

MUTAG 数据集根据其对细菌的诱变作用分为两类。节点类型包括碳、氮、氧、氟、碘、氯和溴。此处不使用边的类型。

MUTAG 包括 188 个分子图,共 3371 个节点(原子)和 7442 个边(化学键)。数据集目录如下

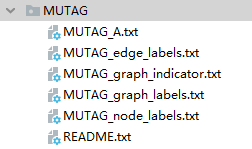
• node_labels.txt 记录了3371个节点中每个节点的类型(编号从0到6)

• graph_indicator.txt 记录每个节点对应的索引号(索引号从1-188编号)

• graph_labels.txt 记录了188个图的对应类型(label为1或-1)

• A.txt记录了7442条边,(start_node_idx,end_node_idx),start_ node_ IDX和end_ node_ IDX在3371范围内

• edge_labels.txt 记录了7442条边以及每条边的类型,这里不使用。

加载数据集的代码如下:

将 numpy 导入为 np

导入 scipy.sparse 作为 sp

进口火炬

def 编码_onehot(标签):

类 u003d 设置(标签)

类_dict u003d {c: np.identity(len(classes))[i, :] for i, c in

枚举(类)}

标签_onehot u003d np.array(列表(地图(类_dict.get,标签)),

dtypeu003dnp.int32)

返回标签_onehot

归一化(mx):

"""行归一化稀疏矩阵"""

rowsum u003d np.array(mx.sum(1))

r_inv u003d np.power(rowsum, -1).flatten()

r_inv[np.isinf(r_inv)] u003d 0。

r_mat_inv u003d sp.diags(r_inv)

mx u003d r_mat_inv.dot(mx)

返回 mx

def load_split_MUTAG_data(pathu003d"datas/MUTAG/", datasetu003d"MUTAG_", split_trainu003d0.7, split_valu003d0.15):

"""加载MUTAG数据"""

print('正在加载 {} 数据集...'.format(dataset))

加载图表的标签

graph_labels u003d np.genfromtxt("{}{}graph_labels.txt".format(path, dataset),

dtypeu003dnp.dtype(int))

图_labels u003d 编码_onehot(图_labels) # (188, 2)

图_labels u003d torch.LongTensor(np.where(graph_labels)[1]) # (188, 1)

图节点的索引号

graph_idx u003d np.genfromtxt("{}{}graph_indicator.txt".format(path, dataset),

dtypeu003dnp.dtype(int))

图_idx u003d np.array(图_idx,dtypeu003dnp.int32)

idx_map u003d {j: i for i, j in enumerate(graph_idx)} # key,value表示key图的起始节点,索引号为value

length u003d len(idx_map.keys()) # 一共有多少张图片

num_nodes u003d [idx_map[n] - idx_map[n - 1] if n - 1 > 1 else idx_map[n] for n in range(1, length + 1)] # 一个长度为188的列表表示每个图中有多少个节点

max_num_nodes u003d max(num_nodes) # 最大的图有多少个节点

功能\列表 u003d []

adj_list u003d []

上一页 u003d 0

节点标签

nodeidx_features u003d np.genfromtxt("{}{}node_labels.txt".format(path, dataset), delimiteru003d",",

dtypeu003dnp.dtype(int))

节点_features u003d np.zeros((nodeidx_features.shape[0], max(nodeidx_features) + 1))

节点_features[np.arange(nodeidx_features.shape[0]), nodeidx_features] u003d 1

边缘信息

边_unordered u003d np.genfromtxt("{}{}A.txt".format(path, dataset), delimiteru003d",",

dtypeu003dnp.int32)

边的标签

边_label u003d np.genfromtxt("{}{}edge_labels.txt".format(path, dataset), delimiteru003d",",

dtypeu003dnp.int32) # 形状 u003d (7442,)

生成邻接矩阵A,包含数据集中的所有边

adj u003d sp.coo_matrix((edges_label, (edges_unordered[:, 0] - 1, edges_unordered[:, 1] - 1)))

论文中a^u003d(d~)^0.5是a~(d~)^0.5的公式

adj u003d adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)

节点_features u003d 标准化(节点_features)

adj u003d normalize(adj + sp.eye(adj.shape[0])) # 对应公式A~u003dA+IN

adj u003d adj.todense()

对于范围内的 n(1,长度 + 1):

entry是第n个图的特征矩阵X

entry u003d np.zeros((max_num_nodes, max(nodeidx_features) + 1))

entry[:idx\map[and] - prev] u003d node\features[prev:idx\map[n]]

entry u003d torch.FloatTensor(entry)

功能_list.append(entry.tolist())

entry是第n个图的邻接矩阵A

条目 u003d np.zeros((max_num_nodes, max_num_nodes))

entry[:idx_map[n] - prev, :idx_map[n] - prev] u003d adj[prev:idx_map[n], prev:idx_map\ [n]]

entry u003d torch.FloatTensor(entry)

adj_list.append(entry.tolist())

prev u003d idx_map[n] # prev是下一个图的起始节点的索引号

数量_total u003d 最大值(图_idx)

数量_train u003d int(拆分_train * 数量_total)

num_val u003d int((split_train + split_val) * num_total)

如果(num_train u003du003d num_val 或 num_val u003du003d num_total):

返回

features\list u003d torch.FloatTensor(features\list)

adj_list u003d torch.FloatTensor(adj_list)

idx_train u003d 范围(数量_train)

idx_val u003d 范围(num_train,num_val)

idx_test u003d 范围(num_val,num_total)

idx_train u003d torch.LongTensor(idx_train)

idx_val u003d torch.LongTensor(idx_val)

idx_test u003d torch.LongTensor(idx_test)

返回值是188个图的邻接矩阵列表,188个图的特征矩阵列表,188个图的标签,每个图的起始节点的索引号,训练集的索引号,

验证集索引号,测试集索引号

返回 adj_list、特征\列表、图形\标签、idx\map、idx_train、idx_val、idx_test

这里有188个图,每个图的邻接矩阵维数为 m a x _ n o d e _ n u m × m a x _ n o d e _ n u m max\_node\_num \times max\_node\_num最大_node_num × 最大_node_num。特征矩阵的维数为 m a x _ n o d e _ n u m × f e a t u r e _ d i m max\_node\_num \times feature\_dim max_node_num×feature_dim

训练 GCN 分类器

这里 f ( . ) f(.) f(.) 由 GCN 表示,模型的代码如下

导入数学

进口火炬

将 torch.nn 导入为 nn

导入 torch.nn.functional 作为 F

从 torch.nn.parameter 导入参数

类 GraphConvolution(nn.Module):

"""

简单的 GCN 层,类似于 https://arxiv.org/abs/1609.02907

论文:半监督分类与图卷积网络

"""

模型的参数包括权重和偏差

def __init__(自我,在_features,out_features):

super(GraphConvolution, self).__init__()

self.in_features u003d 在_features

self.in_features u003d out_features

self.weight u003d Parameter(torch.FloatTensor(in_features, out_features))

self.bias u003d Parameter(torch.FloatTensor(out_features))

self.reset_parameters()

权重初始化

def 重置_参数(自我):

stdv u003d 1./math.sqrt(self.weight.size(1))

self.weight.data.uniform_(-stdv, stdv)

self.bias.data.uniform_(-stdv, stdv)

类似于 tostring

def __repr__(自我):

返回自我。__class__.__name__ + ' (' \

• str(self.in_features) + ' -> ' \

• str(self.out_features) + ')'

计算 A~ X W(0)

def forward(自我,输入,调整):

input.shape u003d [max_node, features] u003d X

adj.shape u003d [max_node, max_node] u003d A~

torch.mm(a, b)是矩阵A和矩阵B的乘积,torch Mul(a,b)是矩阵A和B对应位的乘积,并且a和B的维度必须相等

支持 u003d torch.mm(输入,self.weight)

输出 u003d torch.spmm(调整,支持)

返回输出 + self.bias

类 GCN(nn.Module):

特征个数;最终分类号

def __init__(自我,nfeat,nclass,辍学):

""" 根据论文 """

""" 3 层 GCN,输出维度分别等于 32、48、64,平均所有节点特征 """

""" 具有 2 个全连接层和隐藏维度设置为 32 的最终分类器 """

""" 激活函数 - ReLu (Mutag) """

超级(GCN,自我)。__init__()

self.dropout u003d 辍学

self.gc1 u003d GraphConvolution(nfeat, 32)

self.gc2 u003d GraphConvolution(32, 48)

self.gc3 u003d GraphConvolution(48, 64)

self.fc1 u003d nn.Linear(64, 32)

self.fc2 u003d nn.Linear(32, nclass)

def forward(self, x, adj):

x.shape u003d [max_node, features]

adj.shape u003d [max_node, max_node]

x u003d F.relu(self.gc1(x, adj))

x u003d F.dropout(x, self.dropout, trainingu003dself.training)

x u003d F.relu(self.gc2(x, adj))

x u003d F.dropout(x, self.dropout, trainingu003dself.training)

x u003d F.relu(self.gc3(x, adj))

y u003d torch.mean(x, 0) #均值作为聚合函数,聚合所有节点的特征

y u003d F.relu(self.fc1(y))

y u003d F.dropout(y, self.dropout, trainingu003dself.training)

y u003d F.softmax(self.fc2(y), dimu003d0)

返回 y

训练 GCN 分类器

from Load_dataset import load_split_MUTAG_data,准确度

从模型导入 GCN

进口时间

将 numpy 导入为 np

进口火炬

导入 torch.optim 作为优化

导入 torch.nn.functional 作为 F

模型_path u003d '模型/gcn_first.pth'

时期 u003d 1000

种子 u003d 200

lr u003d 0.001

辍学 u003d 0.1

重量_decay u003d 5e-4

np.random.seed(种子)

torch.manual_seed(种子)

torch.cuda.manual_seed(种子)

类 EarlyStopping():

def __init__(自我,耐心u003d10,min_lossu003d0.5,hit_min_before_stoppingu003dFalse):

self.patience u003d 耐心

self.counter u003d 0

self.hit_min\before\stopping u003d 命中_min\before\stopping

如果命中\min\before\stopping:

self.min_loss u003d min_loss

self.best_loss u003d 无

self.early_stop u003d 假

def __call__(自我,损失):

如果 self.best_loss 为无:

self.best_loss u003d 损失

elif 损失 > self.best_loss:

self.counter +u003d 1

如果 self.counter > self.patience:

if self.hit\min\before\stopping u003du003d True and loss > self.min_loss:

print("不能命中均值损失,将继续")

self.counter -u003d self.patience

其他:

self.early_stop u003d True

其他:

self.best_loss u003d 损失

计数器 u003d 0

如果 __name__ u003du003d '__main__':

adj_list: [188, 29, 29]

特征_list: [188, 29, 7]

图_标签:[188]

adj_list, features\list, graph\labels, idx\map, idx_train, idx_val, idx_test u003d load\split_MUTAG_data()

idx_train u003d torch.cat([idx_train, idx_val, idx_test])

模型 u003d GCN(nfeatu003dfeatures_list[0].shape[1], #nfeat u003d 7

nclassu003dgraph_labels.max().item() + 1, # nclass u003d 2

辍学u003d辍学)

优化器 u003d optim.Adam(model.parameters(),

lru003dlr, 重量_decayu003d重量_decay)

模型.cuda()

功能_list u003d 功能_list.cuda()

adj_list u003d adj_list.cuda()

图_labels u003d 图_labels.cuda()

idx_train u003d idx_train.cuda()

idx_val u003d idx_val.cuda()

idx_test u003d idx_test.cuda()

训练模型

early\stopping u003d Early Stopping(10, hit_min\before\stoppingu003dTrue)

t_total u003d time.time()

对于范围内的纪元(纪元):

t u003d time.time()

模型.train()

优化器.zero_grad()

# 拆分

输出 u003d []

对于 idx_train 中的 i:

输出 u003d 模型(特征_list[i],adj_list[i])

输出 u003d output.unsqueeze(0)

输出。附加(输出)

输出 u003d torch.cat(输出,暗淡 u003d 0)

损失_train u003d F.cross_entropy(输出,图_labels[idx_train])

acc_train u003d 准确度(输出,图_labels[idx_train])

损失_train.backward()

优化器.step()

模型.eval()

输出 u003d []

对于 idx_val 中的 i:

输出 u003d 模型(特征_list[i],adj_list[i])

输出 u003d output.unsqueeze(0)

输出。附加(输出)

输出 u003d torch.cat(输出,暗淡 u003d 0)

损失_val u003d F.cross_entropy(输出,图_labels[idx_val])

acc_val u003d 准确度(输出,图形_labels[idx_val])

print('Epoch: {:04d}'.format(epoch + 1),

'loss_train: {:.4f}'.format(loss_train.item()),

'acc_train: {:.4f}'.format(acc_train.item()),

'loss_val: {:.4f}'.format(loss_val.item()),

'acc_val: {:.4f}'.format(acc_val.item()),

'时间:{:.4f}s'.format(time.time() - t))

打印(损失_val)

早期_stopping(损失_val)

如果 early_stopping.early_stop u003du003d True:

休息

print("优化完成!")

print("经过的总时间:{:.4f}s".format(time.time() - t_total))

火炬.保存(模型.状态_dict(),模型_路径)

训练图生成器

生成器类定义

进口随机

导入副本

将 numpy 导入为 np

进口火炬

将 torch.nn 导入为 nn

导入 torch.nn.functional 作为 F

从模型导入GraphConvolution,GCN

推出 u003d 10

最大_gen_step u003d 10

MAX_NUM_NODES u003d 28 # 用于 mutag

随机种子(200)

类生成器(nn.Module):

def __init__(self, model_path: str, C: list, node_feature_dim: int,num_class u003d 2, cu003d0, hyp1u003d1, hyp2u003d2, start u003d无,nfeatu003d7,辍学u003d0.1):

"""

:param C: 候选节点集(列表)

:param start: 起始节点(默认为随机节点)

"""

超级(发电机,自我)。__init__()

self.nfeat u003d nfeat

self.dropout u003d 辍学

自我.c u003d c

self.fc u003d nn.Linear(nfeat, 8)

self.gc1 u003d GraphConvolution(8, 16)

self.gc2 u003d GraphConvolution(16, 24)

self.gc3 u003d GraphConvolution(24, 32)

MLP1

2 个隐藏维度为 16 的 FC 层

self.mlp1 u003d nn.Sequential(nn.Linear(32, 16), nn.Linear(16, 1))

#MLP2

2 个隐藏维度为 24 的 FC 层

self.mlp2 u003d nn.Sequential(nn.Linear(64, 24), nn.Linear(24, 1))

超参数

self.hyp1 u003d hyp1

self.hyp2 u003d hyp2

self.candidate_set u003d C

默认起始节点(如果有)

如果 start 不是 None:

self.start u003d 开始

self.random_start u003d 假

其他:

self.start u003d random.choice(np.arange(0, len(self.candidate_set)))

self.random_start u003d True

加载 GCN 计算奖励

self.model u003d GCN(nfeatu003dnode_feature_dim,

nclassu003dnum_class,

辍学u003d辍学)

self.model.load\state\dict(torch.load(model_path))

对于 self.model.parameters() 中的参数:

param.requires_grad u003d False

self.reset_graph()

def 重置_graph(自我):

"""

Reset g.G to default graph with only start node, 生成只有一个节点的图

"""

如果 self.random_start u003du003d True:

self.start u003d random.choice(np.arange(0, len(self.candidate_set)))

初始图除了第一个节点外被掩码,其中邻接矩阵的边长为MAX_NUM_NODES + len(self.candidate_set),所以掩码不仅是候选集合点,也是图中所有虚拟节点

掩码_start u003d torch.BoolTensor(

[False if i u003du003d 0 else True for i in range(MAX_NUM_NODES + len(self.candidate_set))])

adj u003d torch.zeros((MAX_NUM_NODES + len(self.candidate_set), MAX_NUM_NODES + len(self.candidate_set)),

dtypeu003dtorch.float32) # 这里的adj形状为[max_num_nodes + len(self.Candidate_set),max_num_nodes + len(self)中间可能有空节点.候选人_set)]

壮举 u003d torch.zeros((MAX_NUM_NODES + len(self.candidate_set), len(self.candidate_set)), dtypeu003dtorch.float32)

壮举[0, self.start] u003d 1

壮举[np.arange(-len(self.candidate_set), 0), np.arange(0, len(self.candidate_set))] u003d 1

度数 u003d torch.zeros(MAX_NUM_NODES)

self.G u003d {'adj': adj, 'feat': 壮举, 'degrees': 度数, 'num_nodes': 1, 'mask_start': mask_start}

计算 GT -> GT + 1

def 前向(自我,G_in):

G_in 是 Gt

G u003d copy.deepcopy(G_in)

x u003d G['feat'].detach().clone() # Gt的特征矩阵

adj u003d G['adj'].detach().clone() # Gt的邻接矩阵

##对应X u003d GCNs(Gt, C)

x u003d F.relu6(self.fc(x))

x u003d F.dropout(x, self.dropout, trainingu003dself.training)

x u003d F.relu6(self.gc1(x, adj))

x u003d F.dropout(x, self.dropout, trainingu003dself.training)

x u003d F.relu6(self.gc2(x, adj))

x u003d F.dropout(x, self.dropout, trainingu003dself.training)

x u003d F.relu6(self.gc3(x, adj))

x u003d F.dropout(x, self.dropout, trainingu003dself.training)

pt,startu003dSoftmax(MLPs(X))

p_start u003d self.mlp1(x)

p_start u003d p_start.masked_fill(G['mask_start'].unsqueeze(1), 0)

p_start u003d F.softmax(p_start, dimu003d0)

a_start_idx u003d torch.argmax(p_start.masked_fill(G['mask_start'].unsqueeze(1), -1))

pt,endu003dSoftmax(MLPs([X,x^start))

广播

x1, x2 u003d torch.broadcast_tensors(x, x[a_start_idx])

x u003d torch.cat((x1, x2), 1) # cat 将 dim 从 32 增加到 64

计算掩码并结束。除了候选集中的节点和没有被选为初始节点的Gt节点,其他的都被屏蔽了

mask_end u003d torch.BoolTensor([True for i in range(MAX_NUM_NODES + len(self.candidate_set))])

掩码_end[MAX_NUM_NODES:] u003d False

掩码_end[:G['num_nodes']] u003d False

掩码_end[a_start_idx] u003d True

p_end u003d self.mlp2(x)

p_end u003d p_end.masked_fill(mask_end.unsqueeze(1), 0)

p_end u003d F.softmax(p_end, dimu003d0)

a_end_idx u003d torch.argmax(p_end.masked_fill(mask_end.unsqueeze(1), -1))

返回新的 G

如果a_end_idx没有被屏蔽,节点存在于图中,没有新节点添加

如果 G['mask_start'][a_end_idx] u003du003d False:

G['adj'][a_end_idx][a_start_idx] +u003d 1

G['adj'][a_start_idx][a_end_idx] +u003d 1

更新度数

G['度'][a_start_idx] +u003d 1

G['degrees'][G['num_nodes']] +u003d 1

其他:

添加节点

G['壮举'][G['num_nodes']] u003d G['壮举'][a_end_idx]

添加边

G['adj'][G['num_nodes']][a_start_idx] +u003d 1

G['adj'][a_start_idx][G['num_nodes']] +u003d 1

更新度数

G['度'][a_start_idx] +u003d 1

G['degrees'][G['num_nodes']] +u003d 1

更新开始掩码

G_mask_start_copy u003d G['mask_start'].detach().clone()

G_mask_start_copy[G['num_nodes']] u003d False

G['mask_start'] u003d G_mask_start_copy

G['num_nodes'] +u003d 1

返回 p_start, a_start_idx, p_end, a_end_idx, G

基于前向函数 G t G_t Gt 计算 G t + 1 G_{t+1} Gt+1 的过程。这里定义分类任务中一个图中的最大节点数_NUM_NODES u003d 28。候选集C C C有7个节点。从 G t G_t Gt # 到 G t + 1 G_{t+1} Gt+1_邻接矩阵的边长为MAX_NUM_NODES + len(candidate set) u003d 35。即有中间是很多虚拟节点(类似于padding)。所以你在戴口罩时必须考虑到这一点。

奖励函数定义如下:

###奖励功能

def 计算_reward(self, G_t_1):

"""

Rtr 根据图表规则计算,以鼓励生成的图表有效

1. 任意两个节点之间只添加一条边

2. 生成的图不能包含比预定义的最大节点数更多的节点

3.(对于化学)度数不能超过化合价

如果生成的图违反了图规则,Rtr u003d -1

来自训练模型的 Rtf 反馈

"""

rtr u003d self.check_graph_rules(G_t_1)

rtf u003d self.calculate_reward_feedback(G_t_1)

rtf_sum u003d 0

对于范围内的 m(推出):

p_start, a_start, p_end, a_end, G_t_1 u003d self.forward(G_t_1)

rtf_sum +u003d self.calculate_reward_feedback(G_t_1)

rtf u003d rtf + rtf_sum * self.hyp1 / rollout

返回 rtf + self.hyp2 * rtr

def 计算_reward_feedback(self, G_t_1):

"""

p(f(G_t_1) u003d c) - 1/l

其中 l 表示 f 的可能类别数

"""

f u003d self.model(G_t_1['feat'], G_t_1['adj'], 无)

返回 f[self.c] - 1 / len(f)

图表规则

def 检查_graph_rules(self, G_t_1):

"""

对于 mutag,节点度数不能超过化合价

"""

idx u003d 0

对于 G_t_1['degrees'] 中的 d:

如果 d 不为 0:

node_id u003d torch.argmax(G_t_1['feat'][idx]) # 例如。 [0, 1, 0, 0] -> 1

node u003d self.candidate_set[node_id] # 例如 ['C.4', 'F.2', 'Br.7'][1] u003d 'F.2'

max_valency u003d int(node.split('.')[1]) # 例如。 C.4 -> ['C', '4'] -> 4

如果任何节点度数超过其化合价,则返回-1

如果 max_valency < d:

返回 -1

返回 0

可以看到

• 图规则只检测一个节点的度数是否超过其原子化学价。如果非法,则返回 - 1,如果合法,则返回 0

损失是

## 计算损失

def 计算_loss(self, Rt, p_start, a_start, p_end, a_end, G_t_1):

"""

由交叉熵损失 (Lce) 和奖励函数 (Rt) 计算得出

其中损失 u003d -Rt*(Lce_start + Lce_end)

"""

Lce_start u003d F.cross_entropy(torch.reshape(p_start, (1, 35)), a_start.unsqueeze(0))

Lce_end u003d F.cross_entropy(torch.reshape(p_end, (1, 35)), a_end.unsqueeze(0))

返回 -Rt * (Lce_start + Lce_end)

• 35 是 MAX_NUM_NODES + len(候选集)u003d 35。

在这里,reward 和 loss 都是 Generator 类的成员函数。

培训代码

从 GraphGenerator 导入生成器

导入副本

将 numpy 导入为 np

将 networkx 导入为 nx

导入 matplotlib.pyplot 作为 plt

进口火炬

导入 torch.optim 作为优化

lr u003d 0.01

b1 u003d 0.9

pa u003d 0.am

hyp1 u003d 1

hyp2 u003d 2

最大_gen_step u003d 10 # T u003d 10

候选_set u003d ['C.4', 'N.5', 'O.2', 'F.1', 'I.7', 'Cl.7', 'Br.5'] # C.4表示碳原子度数不超过4

模型_path u003d '模型/gcn_first.pth'

训练生成器

def train_generator(cu003d0, max_nodesu003d5):

g.c u003d c

对于范围内的 i (max_gen_step):

优化器.zero_grad()

G u003d copy.deepcopy(g.G)

p_start, a_start, p_end, a_end, G u003d g.forward(G)

Rt u003d g.calculate_reward(G)

损失 u003d g.calculate_loss(Rt, p_start, a_start, p_end, a_end, G)

loss.backward()

优化器.step()

如果 G['num_nodes'] > max_nodes:

g.reset_graph()

elif Rt > 0:

g.G u003d G

生成图表

def 生成_graph(cu003d0, max_nodesu003d5):

g.c u003d c

g.reset_graph()

对于范围内的 i (max_gen_step):

G u003d copy.deepcopy(g.G)

p_start, a_start, p_end, a_end, G u003d g.forward(G)

Rt u003d g.calculate_reward(G)

如果 G['num_nodes'] > max_nodes:

返回 g.G

elif Rt > 0:

g.G u003d G

返回 g.G

##画图

def 显示_graph(G):

G_nx u003d nx.from_numpy_matrix(np.asmatrix(G['adj'][:G['num_nodes'], :G['num_nodes'] ].numpy()))

nx.draw_networkx(G_nx)

布局u003dnx.spring_layout(G_nx)

nx.draw(G_nx, 布局)

着色u003dtorch.argmax(G['壮举'],1)

颜色u003d['b','g','r','c','m','y','k']

对于范围内的 i (7):

nx.draw_networkx_nodes(G_nx,posu003dlayout,nodelistu003d[x for x in G_nx.nodes() if coloring[x]u003du003di],node_coloru003dcolors [一世])

nx.draw_networkx_labels(G_nx,posu003dlayout,labelsu003d{x:candidate_set[i].split('.')[0] for x in G_nx.nodes () 如果着色[x]u003du003di})

nx.draw_networkx_edges(G_nx,posu003dlayout,widthu003dlist(nx.get_edge_attributes(G_nx,'weight').values()))

nx.draw_networkx_edge_labels(G_nx,posu003dlayout,edge_labelsu003dnx.get_edge_attributes(G_nx,“权重”))

plt.show()

如果 __name__ u003du003d '__main__':

g u003d 生成器(模型_path u003d 模型_path,C u003d 候选_set,节点_feature_dimu003d7,cu003d0,开始u003d0)

优化器 u003d optim.Adam(g.parameters(), lru003dlr, betasu003d(b1, b2))

对于范围内的 i (1, 10):

##分别生成最多i个节点的图结构

g.reset_graph()

训练_generator(cu003d1, max_nodesu003di)

to_display u003d 生成_graph(cu003d1, max_nodesu003di)

显示_graph(到_display)

print(g.model(to_display['feat'], to_display['adj']))

这里的训练过程不能用数据来评价,只能画出来。这里,分别生成包含1-9个节点的GCN分类模型 f ( . ) f(.) f(.) 预测为1的子图结构,并给出1的概率。给出结果如下

1个概率:0.7715

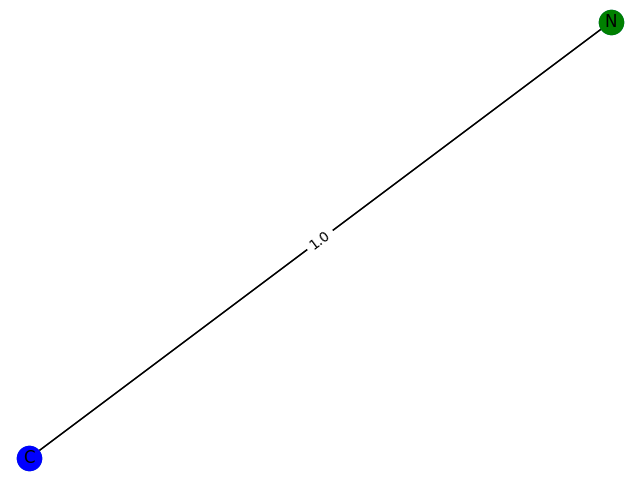
2\。概率:0.7935

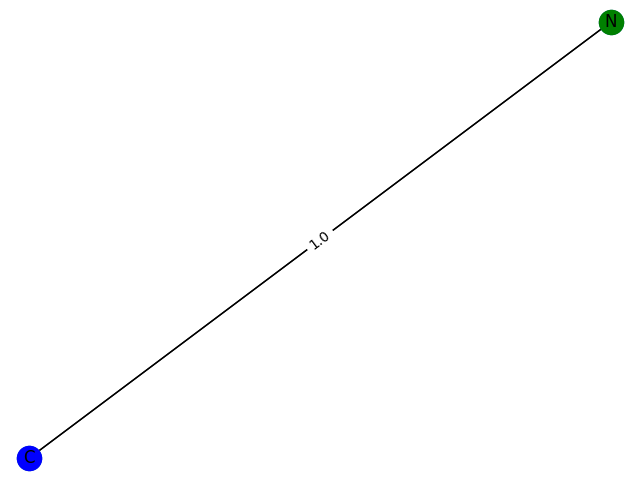
3\。概率:0.8358

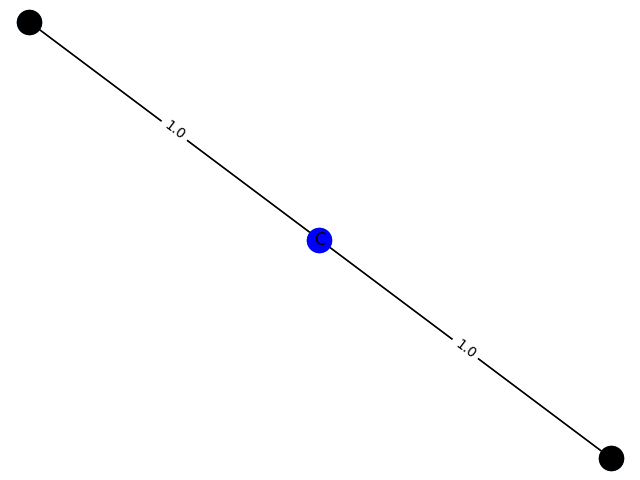
4 概率:0.8556

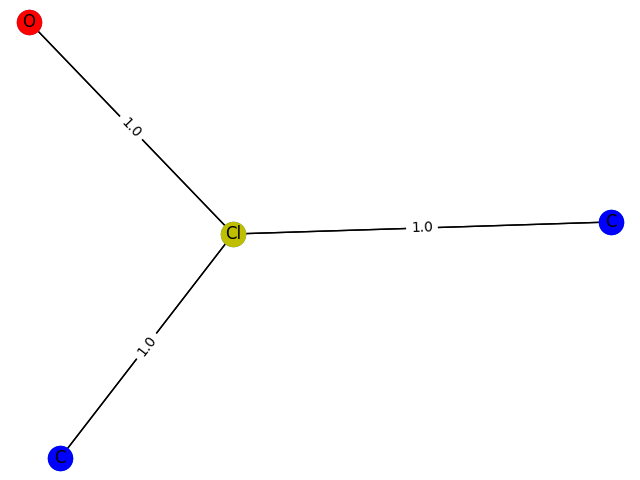
5概率:0.8778

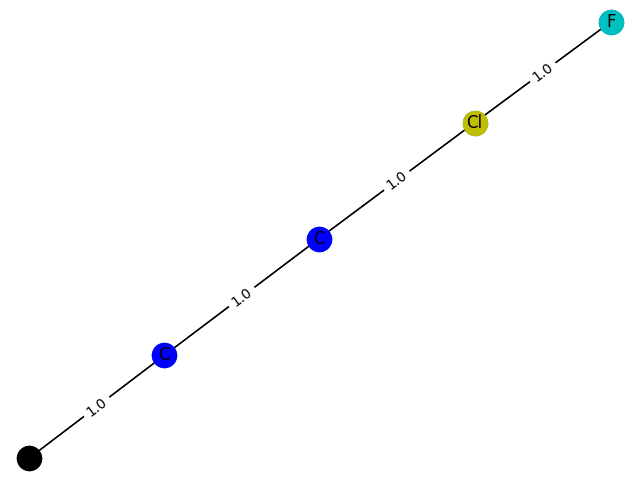
6概率:0.8533

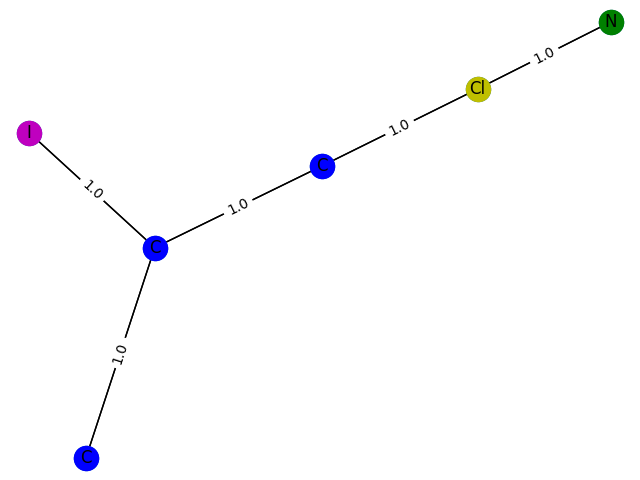
7 概率:0.9010

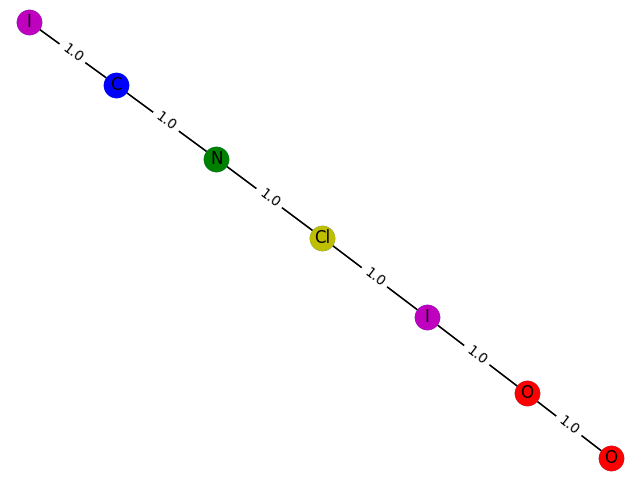
8概率:0.9005

! zoz100078](https://programming.vip/images/doc/ced618bb82bc5ecbebf45bd40c9c59ba.jpg)

9 概率:0.8510

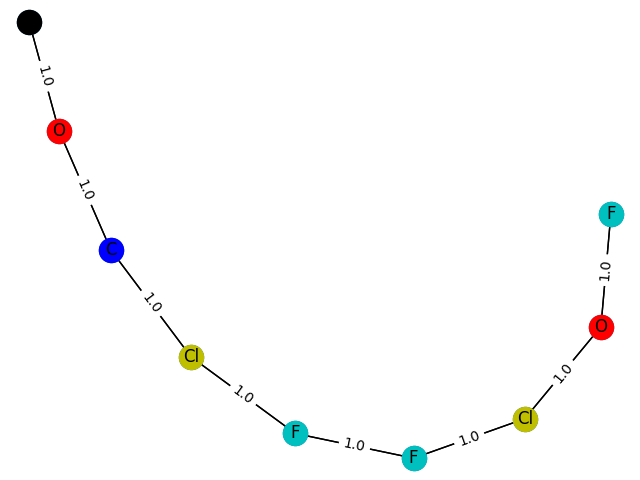
与纸的差距还是比较明显的。参数的调整还是很有学问的。也许我太优秀了,无法掌握。

参考

[1] H. Yuan、J. Tang、X. Hu 和 S. Ji,“XGNN:图神经网络的模型级解释”,序列号。 KDD'20。美国纽约州纽约市:计算机协会,2020 年,p。 430–438.[在线]。可用:https://doi.org/10.1145/3394486.3403085