机器学习A-Z学习笔记16汤普森采样算法

1.简单原理

本文继续讨论一种强化学习算法,称为 Thompson 采样算法。该算法的数学理论基础是贝叶斯推理。先说一下这个算法的基本原理,同样以多臂老虎机为例

采样算法计算流程

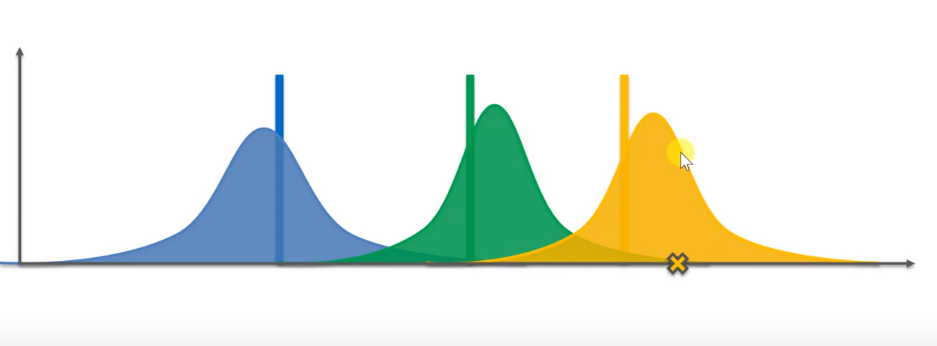
如图,横轴代表奖励,越靠右表示奖励越多。三条垂直线代表三台不同的老虎机及其平均奖励。

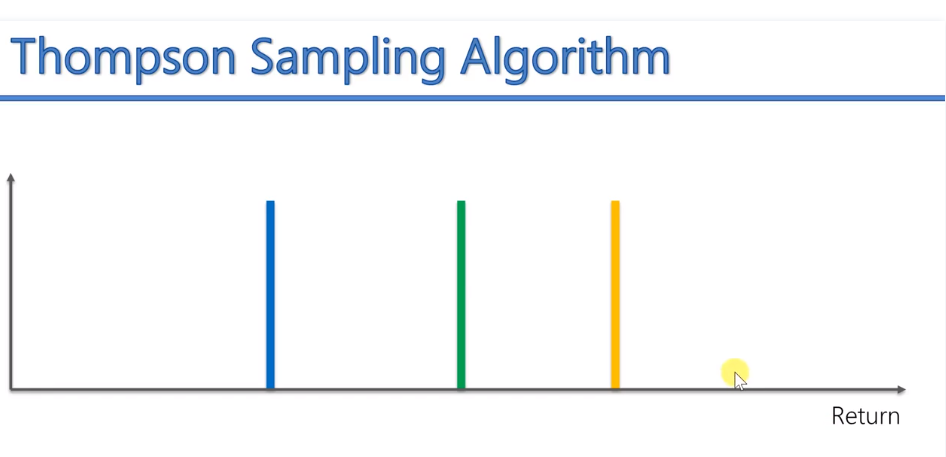
在算法开始之前,我们什么都不知道,所以我们需要得到一些基础数据。根据四台老虎机的数据,你可以根据蓝色分配获得若干奖励。同样,绿色老虎机也可以获得分配,黄色也是如此。

这三个分布预测了三台机器给我们带来回报的数学期望的概率分布。接下来,基于这三个随机分布,我们得到几个随机样本。选择获得最大采样值的机器并按下它。但是,由于是随机的,虽然黄色的实际期望值最高,但我们仍然可能会选择绿色大于黄色的结果。

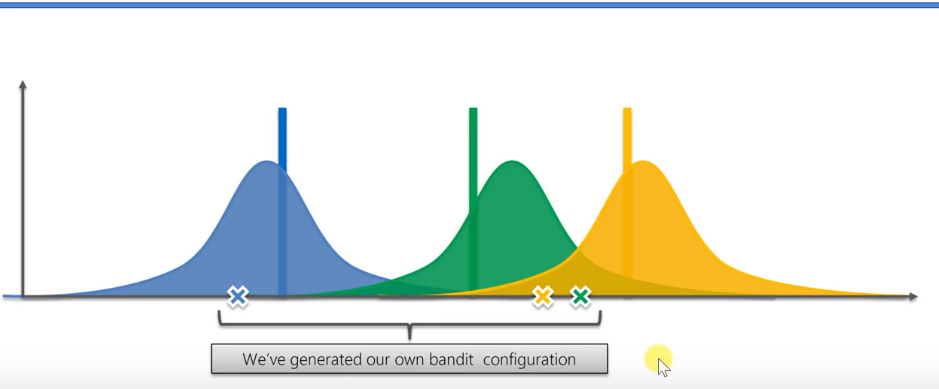
按下后,我们将得到一个新的观察奖励值。得到新的奖励值后,我们需要调整绿机的分配。

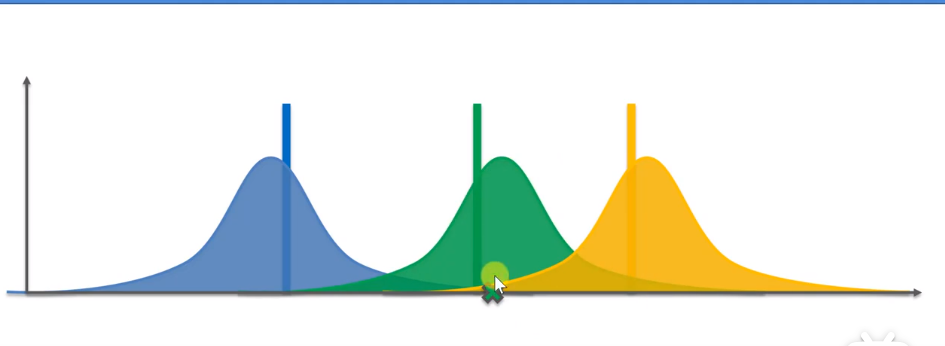
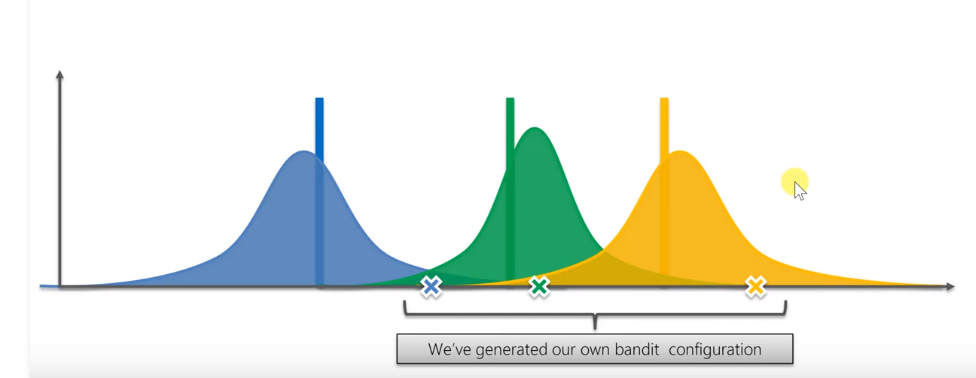
显然,绿色分布变得更高和更窄。以下步骤实际上与此处相同。仍然选择奖励值最高的机器,按下它,通过得到的结果继续调整分配。

当游戏经过很多步骤时,这些分布会变得很窄,尤其是黄色的会基本符合实际预期

! zoz100037](https://programming.vip/images/doc/86ebb4f5edb17a52a8bdd90b0a99200f.jpg)

这时候因为我们总是选择奖励值最高的机器,所以按黄色的概率会比较高,导致黄色的会越来越窄,而蓝色的很少玩,所以应该是相对较宽。

Thompson 采样算法 vs. 置信区间上限算法

我们使用 Thompson 采样算法和 ucb 算法来处理多臂老虎机问题。现在让我们比较接下来的两种算法。我们来看看这两种算法的基本原理图。

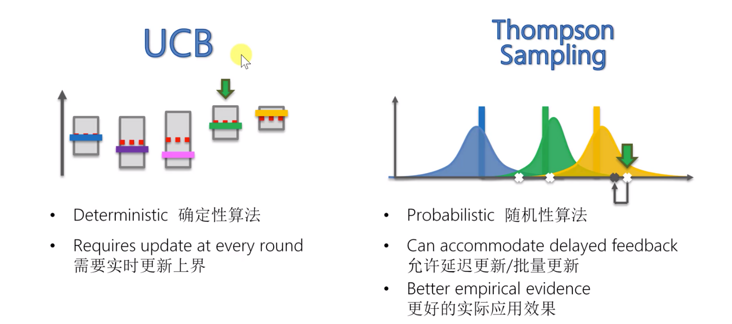
首先,这个UCB算法是一种确定性算法。当我们得到相同的奖励时,我们的决定就确定了。因此,我们的总收入和每一轮的总收入是确定的。每一轮做出的决定只与置信区间的上限有关,它只与机器的所有观察结果有关。所以当所有机器的观察值相同时,我们总是会做出相同的决定。对于 Thompson 算法,它是一种随机算法。它的一个或多个步骤由与运气有关的随机函数控制。这取决于一些随机事件。比如我们在上面选取点的时候,虽然黄色的实际期望值大于绿色,但我们仍然可能选取绿色大于黄色的数据点。因此,它是一种随机算法。

UCB的另一个特点是它需要实时更新上界,这在之前的文章中描述UCB算法的原理时就可以看出。对于 Thompson 采样算法,它允许延迟更新甚至批量更新。例如,我们在互联网上投放了一批广告。在这里,可以得到延迟的结果。最后,在近几年的实际应用和研究中,发现Thompson采样算法比置信区间算法具有更好的实际应用效果。

2.相关代码

# 汤普森抽样

导入库

将 numpy 导入为 np

导入 matplotlib.pyplot 作为 plt

将熊猫导入为 pd

导入数据集

数据集 u003d pd.read_csv('Ads_CTR_Optimisation.csv')

实现汤普森抽样

进口随机

N u003d 10000

d u003d 10

广告_selected u003d []

数量\of_ 奖励_1 u003d [0] * d

数量\of_ 奖励_0 u003d [0] * d

总计_reward u003d 0

对于范围内的 n (0, N):

广告 u003d 0

最大_随机 u003d 0

对于范围内的 i (0, d):

本轮广告i产生的概率(通过累计点击次数和非点击次数,基于贝叶斯推理)

随机_beta u003d random.betavariate(numbers_of_rewards_1[i] + 1, numbers_of_rewards_0[i] + 1)

如果本轮广告i概率最高,则选择推送

如果随机_beta > 最大_随机:

最大_random u003d 随机_beta

广告 u003d 我

日志记录

广告_selected.append(广告)

确认客户的点击结果

奖励 u003d dataset.values[n, ad]

如果i更新,i为累计读取点数

如果奖励 u003du003d 1:

数量_ of_ 奖励_1[ad] u003d 数量_ of_ 奖励_1[ad] + 1

如果点击结果为1,则更新累计未点击的广告i个数

其他:

数量_ of_ 奖励_0[ad] u003d 数量_ of_ 奖励_0[ad] + 1

#更新总奖项

总计_reward u003d 总计_reward + 奖励

可视化结果 - 直方图

plt.hist(广告_selected)

plt.title('广告选择的直方图')

plt.xlabel('广告')

plt.ylabel('每个广告被选中的次数')

plt.show()