Python 中的损失函数是任何机器学习模型的组成部分。这些函数告诉我们模型的预测输出与实际输出的差异有多大。

有多种计算这种差异的方法。在本教程中,我们将研究一些更流行的损失函数。

我们将在本教程中讨论以下四个损失函数。

1.均方误差

2. 均方根误差

3. 平均绝对误差

4. 交叉熵损失

在这 4 个损失函数中,前三个适用于回归,最后一个适用于分类模型的情况。

在 Python 中实现损失函数

让我们看看如何在 Python 中实现这些损失函数。

1.均方误差 (MSE)

均方误差 (MSE) 计算为预测值与实际观察值之间差异的平方的平均值。在数学上,我们可以将其表示如下:

均方误差

MSE 的 Python 实现如下:

import numpy as np
def mean_squared_error(act, pred):

   diff = pred - act
   differences_squared = diff ** 2
   mean_diff = differences_squared.mean()
   
   return mean_diff

act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])

print(mean_squared_error(act,pred))

输出 :

0.04666666666666667

您也可以使用 sklearn 中的mean_squared_error来计算 MSE。该函数的工作原理如下:

from sklearn.metrics import mean_squared_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_squared_error(act, pred)

输出 :

0.04666666666666667

2.均方根误差 (RMSE)

均方根误差 (RMSE) 计算为均方误差的平方根。在数学上,我们可以将其表示如下:

均方根误差

RMSE 的 Python 实现如下:

import numpy as np
def root_mean_squared_error(act, pred):

   diff = pred - act
   differences_squared = diff ** 2
   mean_diff = differences_squared.mean()
   rmse_val = np.sqrt(mean_diff)
   return rmse_val

act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])

print(root_mean_squared_error(act,pred))

输出 :

0.21602468994692867

您也可以使用 sklearn 中的mean_squared_error来计算 RMSE。让我们看看如何使用相同的函数实现 RMSE:

from sklearn.metrics import mean_squared_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_squared_error(act, pred, squared = False)

输出 :

0.21602468994692867

如果参数“squared”设置为True,则函数返回MSE值。如果设置为 False, 函数返回 RMSE 值。

3.平均绝对误差 (MAE)

平均绝对误差 (MAE) 计算为预测值和实际观测值之间的绝对差值的平均值。在数学上,我们可以将其表示如下:

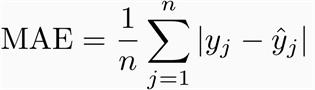
MAE

** MAE 的 Python 实现如下:**

import numpy as np
def mean_absolute_error(act, pred):
    diff = pred - act
    abs_diff = np.absolute(diff)
    mean_diff = abs_diff.mean()
    return mean_diff

act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_absolute_error(act,pred)

输出 :

0.20000000000000004

您也可以使用来自 sklearn 的mean_absolute_error来计算 MAE。

from sklearn.metrics import mean_absolute_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_absolute_error(act, pred)

输出 :

0.20000000000000004

4. Python中的交叉熵损失函数

交叉熵损失也称为负对数似然。这最常用于分类问题。分类问题是您将示例分类为属于两个以上类别之一的问题。

让我们看看在二分类问题的情况下如何计算误差。

让我们考虑一个分类问题,其中模型试图在狗和猫之间进行分类。

查找错误的python代码如下。

from sklearn.metrics import log_loss
log_loss(["Dog", "Cat", "Cat", "Dog"],[[.1, .9], [.9, .1], [.8, .2], [.35, .65]])

输出 :

0.21616187468057912

我们正在使用来自 sklearn 的log_loss方法。

函数调用中的第一个参数是每个输入的正确类标签列表。第二个参数是模型预测的概率列表。

概率采用以下格式:

[P(dog), P(cat)]

结论

本教程是关于 Python 中的损失函数的。我们涵盖了回归和分类问题的不同损失函数。希望您和我们一起学习愉快!