人脑是开发神经网络的模型,因为它可以充分学习、理解和解决复杂的问题。这种对大脑本质的理解催生了人工神经网络 (ANN) 的概念,该概念由 Warren McCulloch(神经科学家)和 Walter Pitts(逻辑学家)于 1943 年首次提出。为了更好地理解 Mcculloch 和 Pitts (MCP) 模型工作,从生物科学中吸取教训,了解大脑是如何工作的。

[](https://res.cloudinary.com/practicaldev/image/fetch/s--cLc7Wl06--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https:// imgur.com/35b34d0.jpeg)

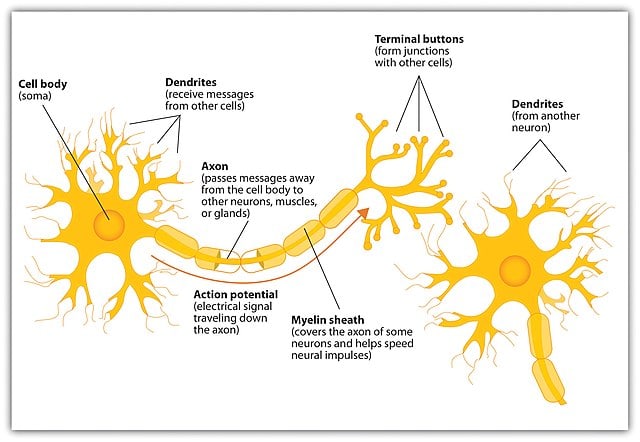
如上所示,在生物神经元中,树突负责接收来自其他细胞的信息/电信号,就像输入设备一样。像 CPU 一样,体细胞负责处理这些信号并返回输出/响应,轴突将这种输出传递给身体的其他神经元和器官。

[](https://res.cloudinary.com/practicaldev/image/fetch/s--yzpsW-ys--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://imgur. com/iiNMnrD.jpeg%2522Image-by-author%2522)

现在,MCP 模型是生物神经元的简化实现。 MCP 的设计使其可以对其输入执行聚合总和 ∑ 并将其与固定阈值 ∮ 进行比较,如果总和大于或小于阈值,则返回零或一的输出。此输出可能对应于特定操作,例如将电子邮件分类为垃圾邮件或非垃圾邮件。但是,MCP 模型有其局限性,即:

• 它只接受二进制输入(0 和 1)。

• 它赋予每一个输入同等的重要性,这未能反映生活事件的运作方式,因为有些事情比其他事情更重要。

• 它不适用于非线性可分离事件。

这些限制导致美国心理学家弗兰克·罗森布拉特在 1958 年提出了感知器。

感知器:单神经网络。

[](https://res.cloudinary.com/practicaldev/image/fetch/s--z21tWb6J--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://imgur.com /cRhK7AA.jpeg)

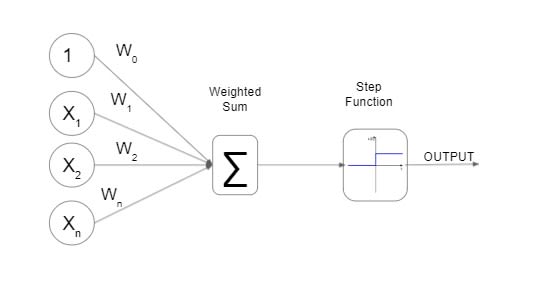
Perceptron 神经网络是一种用于二元线性分类的监督学习算法。它由四个部分组成:

• 个输入。

• 权重和偏差。

• 激活功能。

• 输出。

这是感知器神经网络的工作原理;

输入乘以它们各自的权重并与偏差 w0 相加。结果称为加权和。这个等式代表了它背后的数学:(1*w0) + (x1*w1) + (x2*w2) + ... + (xn*wn)。权重的目的是什么?权重显示每个输入的重要性。输入的权重越高,它对最终结果的影响就越大。假设您正在训练感知器来分类电子邮件是否为垃圾邮件。如果表示发送到多个帐户的电子邮件的输入 x1 的权重 w1 为 10,则它将对感知器的最终输出产生更大的影响。

在计算加权和后,感知器将其传递给激活函数。激活函数是一个非线性函数,它将加权和转换为一个值范围,例如,0 到 1(sigmoid 函数),-1 到 +1(tanh 函数),0 到无穷大(Relu 函数)。这种转换有助于感知器学习数据中的复杂性并决定执行或不执行什么动作,也称为决定触发或不触发的神经元。

偏见的目的如何?偏差是一个常数值,类似于直线方程 $$y u003d mx + c$$ 中的截距 c,它有助于将激活向左或向右移动,这对于决定神经元是否火灾与否。看一下这个进一步解释的例子:在计算一组输入的加权和后,你会得到 -0.35 的值,但神经元不会对任何小于零的输出执行任何动作(触发)。为了确保神经元为这组输入触发,您需要在加权和中添加一个偏差,例如 1,给出 0.65 的值,从而导致神经元触发。

Python 中的感知器实现。

在本节中,您将看到如何实现一个感知器神经网络,该网络根据其输入来决定它是否触发。

x_inputs = [1.2, 0.8, -0.7]
w_weights = [1, 0.87, -0.2]


def activating_step_function(weighted_sum):
    if weighted_sum > 0:
        return 1
    else:
        return 0


def neuron_fire_or_not(value_activation_function):
    if value_activation_function <= 0:
        return "Do Not Fire Neuron"
    else:
        return "Fire Neuron"

def perceptron():

    weighted_sum = 0

    for x, w in zip(x_inputs, w_weights):
        weighted_sum += x*w
        print(weighted_sum)

    value_activation_function = activating_step_function(weighted_sum)

    return neuron_fire_or_not(value_activation_function)

if "__main__" == "__name":
    perceptron()

进入全屏模式 退出全屏模式

在上面的演示中,加权和是在perceptron_function中通过将输入乘以它们各自随机设置的权重来计算的。然后将加权和传递给activation_step_function并为每个小于或等于零的加权和返回 0,如果大于零则输出 1。来自activation_step_function的值被进一步传递给neuron_fire_or_not函数,并为每个大于零的值触发神经元。运行代码,看看会发生什么。

输出:

1.2
1.896
2.036
'Fire Neuron'

进入全屏模式 退出全屏模式

通过在每次迭代中打印加权和,您会看到加权和的最终值为 2.036。由于最终总和大于 0,神经元将被激活(被激发)。

多层感知器。

类似于 MCP 模型的感知器神经网络有其局限性。一方面,它只能返回二进制值 0 和 1,作为二进制分类器,并且只能针对线性可分离问题进行训练。

[](https://res.cloudinary.com/practicaldev/image/fetch/s--EXDVdvBy--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://imgur.com /e71YsaJ.jpeg)

假设红点和蓝点是您要解决的问题的两个不同类别,例如垃圾邮件分类。红点代表垃圾邮件,蓝点代表非垃圾邮件。左边的图表是线性可分的,因为您可以画一条线来分离两个类。但是对于右侧的图像,您无法绘制一条将两个类明显分开的线。单个感知器神经网络将解决左侧的问题,但不能解决右侧的问题。

[的图像](https://res.cloudinary.com/practicaldev/image/fetch/s--2UPg0Z-6--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https: //imgur.com/KeIJEYy.jpeg)

这些限制导致了多层感知器 (MLP) 神经网络的发展。 MLP 包括两个或多个组合的单个感知器神经网络。它具有三层,输入层、隐藏层和输出层,一层中的每个节点(您在上图中看到的圆圈)完全连接到下一层中的每个节点,使其成为全连接神经网络。有了这种结构,多层感知器将在每个网络层具有多个权重和偏差。这种复杂程度和复杂性允许多层感知器神经网络解决线性和非线性可分离问题。

回顾。

• 人脑启发了神经网络的第一个模型——Mcculloch 和 Pitts (MCP) 模型。

• Frank Rosenblatt 在 1958 年发明了感知器神经网络,以克服 MCP 模型的局限性。

• 感知器包括输入、权重和偏差、激活函数和输出。

• 感知器也受到限制,因为它只能输出二进制值(0 和 1)并且只能解决线性可分问题。

• 多层感知器 (MLP) 通过组合两个或多个感知器克服了单层感知器的限制。

• MLP 具有输入层、隐藏层和输出层。

感谢您阅读本文,如果您喜欢它,请务必喜欢它。

您可以关注Twitter和LinkedIn以了解有关机器学习和人工智能世界的更多信息,如果您有任何问题,请在下方发表评论。