在这个最终花了几个月的周末项目中,我结合了三种爱好:中文、编程和 3D 打印。

我想知道是否可以生成一个高度代表书写顺序的汉字的 3D 模型。

结果

您可以生成的一些示例:

工作原理

读汉字的轮廓

对于这里的所有示例,我将使用字符 好 (hăo)。它的意思是“好”,是你好(nĭ hăo)的第二部分,中文意思是“你好”。好用常见的字体如下所示:

每个汉字都是用多笔书写的,笔画的顺序对于使汉字在视觉上正确很重要。好,有6招。

[](https://res.cloudinary.com/practicaldev/image/fetch/s--AQG06BOY--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_66%2Cw_880/https://dev-to-uploads。 s3.amazonaws.com/uploads/articles/7kujkrafetbmdlfa9adp.gif)

6招的好。来源:汉字作家

在Make me a Hanzi上有一个很棒的中文笔画数据库。每个字符都在 JSON 中定义,例如:

{
  "character": "好",
  "strokes": ["M 330 202 Q 361 175 399 134 Q 415 119 424 118 Q 433 118 439 128 Q 446 138 442 170 Q 435 206 361 247 L 319 270 Q 292 286 258 304 Q 237 314 240 335 Q 261 393 281 453 L 293 492 Q 317 568 337 644 Q 347 690 366 715 Q 379 737 373 750 Q 360 769 313 797 Q 294 810 276 801 Q 263 794 273 778 Q 303 733 247 486 L 236 442 Q 218 373 195 336 Q 185 314 206 296 Q 254 268 294 233 L 330 202 Z","M 294 233 Q 287 226 281 217 Q 250 180 196 143 Q 183 134 165 124 Q 149 114 133 104 Q 120 95 131 92 Q 212 86 327 199 Q 328 200 330 202 L 361 247 Q 406 322 421 385 Q 449 488 463 510 Q 473 526 458 537 Q 416 576 387 569 Q 374 565 378 550 Q 387 531 387 507 L 385 481 Q 384 469 382 455 Q 375 376 319 270 L 294 233 Z","M 387 507 Q 341 501 293 492 L 247 486 Q 183 479 115 468 Q 94 465 61 471 Q 48 471 45 462 Q 41 450 49 441 Q 68 422 96 400 Q 106 396 118 402 Q 190 436 236 442 L 281 453 Q 320 463 362 474 Q 372 478 385 481 C 414 489 417 511 387 507 Z","M 671 521 Q 788 635 822 648 Q 843 655 835 672 Q 831 688 760 725 Q 739 735 716 725 Q 661 703 575 676 Q 553 669 498 669 Q 473 669 482 648 Q 491 635 511 623 Q 544 605 578 627 Q 597 636 691 676 Q 706 682 719 673 Q 732 664 726 649 Q 693 595 655 531 C 640 505 649 500 671 521 Z","M 717 430 Q 702 497 671 521 L 655 531 Q 648 535 640 538 Q 618 547 608 540 Q 595 533 608 519 Q 645 491 653 444 Q 656 434 659 421 L 668 384 Q 701 204 658 103 Q 643 76 607 83 Q 576 89 548 94 Q 536 97 542 85 Q 546 78 564 65 Q 604 31 618 5 Q 628 -14 645 -11 Q 660 -10 687 17 Q 775 107 726 391 L 717 430 Z","M 726 391 Q 783 397 947 397 Q 966 398 971 406 Q 977 416 960 430 Q 909 467 848 454 Q 793 445 717 430 L 659 421 Q 562 409 452 393 Q 431 392 447 375 Q 460 362 478 357 Q 497 351 514 356 Q 586 375 668 384 L 726 391 Z"],
  "medians": [[[282,788],[307,769],[327,733],[264,465],[216,321],[235,298],[386,194],[411,166],[424,133]],[[390,556],[417,530],[424,516],[422,504],[387,361],[338,255],[304,207],[260,165],[206,127],[137,97]],[[59,457],[107,434],[373,491],[380,501]],[[493,656],[517,646],[550,644],[680,692],[706,699],[743,696],[771,669],[765,657],[677,546],[674,535],[663,536]],[[613,530],[637,519],[659,499],[674,474],[687,432],[711,289],[709,166],[692,92],[672,59],[648,41],[551,85]],[[449,384],[504,377],[860,427],[906,426],[960,412]]]
}

进入全屏模式 退出全屏模式

这个字符(好)的笔画轮廓在strokes数组中定义。它们以 SVG 路径格式存储。

每个笔划的中位数在medians数组中定义。

有 6 个笔画,因此每个数组包含 6 个项目。

所有点都在 1024x1024 网格上。

让我们使用 Python 库 Svgpathtools 读取这些数据:

import parse_path from svgpathtools
stroke_path = parse_path(character_data["strokes"][0])

进入全屏模式 退出全屏模式

Svgpathtools 给我们一个 Path 对象。要使用 Matplotlib 绘制这些笔画,我们需要在该笔画上采样一些点:

points = []
# for every segment in the path...
for segment in stroke_path:
    # take 4 samples
    for i in [0, 0.25, 0.5, 0.75]
        point = segment.point(i)
        ps.append(point)
points.append(points[0])
xs_stroke, ys_stroke = zip(*points)
plt(xs_stroke, ys_stroke, "g-")

进入全屏模式 退出全屏模式

这将绘制笔画的轮廓。我们还可以绘制中位数:

xs_medians, ys_medians = zip(*character_data["medians"][0])
plt(xs_medians, ys_medians, "ro", markersize=2)

进入全屏模式 退出全屏模式

经过一些子图和对齐后,我们得到了这个:

伟大的!现在我们如何把它变成 3D 对象?

好吧,我们可以尝试使用 SolidPython,一个输出 OpenSCAD 的库,一种用于创建 3D 对象的语言。

stroke_polygon = polygon(stroke_points)
stroke_obj = linear_extrude(10)(stroke_polygon)

进入全屏模式 退出全屏模式

如果我们对字符中的每个笔画都这样做,我们会得到以下输出:

每一笔都好,线性挤压

不错。但我们想在这里生成实际的 3D 对象,而不是无聊的平面形状。

我们需要一种方法将每个笔划分成大小大致相等的部分。

将字符切割成零件

所以我们接下来的步骤需要等距的点,笔画的每个部分都需要一个点。

幸运的是,Svgpathtools 使我们可以轻松地对给定 0 到 1 之间的数字的路径上的点的位置进行采样:

# create Svgpathtools Lines out of the medians
medians_lines = [Line(p1, p2) for p1, p2 in pairwise(medians)]
# create a Path out of those lines
medians_path = Path(*medians_lines)
# sample the Path
median_points = [medians_path.point(i) for i in np.linspace(0, 1, parts_count)]

进入全屏模式 退出全屏模式

如果我们现在也用蓝色绘制这些点,我们会得到:

现在我们现在大致应该如何划分我们的笔划。但是我们如何实际计算形状呢?为此,我们可以使用 Voronoi 图。

因为我们想要封闭的 Voronoi 区域(不是延伸到无穷大的区域),所以我们在形状周围添加了 4 个额外的点,在一定距离处,它们不会干扰中心 1024x1024 正方形内的 Voronoi 图。

缩小,看起来像这样:

如果我们现在将这些多边形与字符相交,线性拉伸每个部分并根据笔划中的距离移动它,我们得到:

[](https://res.cloudinary.com/practicaldev/image/fetch/s--NSogLWj9--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://dev-to -uploads.s3.amazonaws.com/uploads/articles/2wopogn5fax7qcq0zbvp.png)

obj += up(z)(
    linear_extrude(thickness)(
        intersection()(voronoi_polygon, strokes_polygon)
    )
)

进入全屏模式 退出全屏模式

不可怕。

如果我们根据部分在笔划中的位置添加一些颜色,它看起来像这样:

[](https://res.cloudinary.com/practicaldev/image/fetch/s--xeM4koUi--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://dev- to-uploads.s3.amazonaws.com/uploads/articles/b2otofkywo1v41tml5ao.png)

现在您可能认为我们可以通过将零件切割成更多零件来增加零件的平滑度,但这在角落里是行不通的。

我们会做一些不同的事情:我们根据斜率倾斜每个部分。

剪切每个零件以产生光滑的表面

3D 中的偏斜通常称为剪切,它可以用称为剪切矩阵的 3D 矩阵表示。

根据维基百科:

来源:https://en.wikipedia.org/wiki/Shear_matrix

我不太明白那是什么意思,但我知道一些矩阵代数。我可以看到输入的第 4 维会影响输出的第 1 维。

如果你推理它,你可以得出结论:如果只有第一个维度受到影响,那么剪切将平行于第一个维度的轴:x 轴。

在我们的例子中,我们需要剪切平行于 z 维度。 xxx 和 yyy 输入将能够影响 zzz 输出。

[# 00ab# ] \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ a & b & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ⎣ ⎡10a001b100001⎦⎤

在这种情况下,输出将偏斜如下: z′\u003da∗x+b∗y+zz' u003d a*x + b*y + zz′\u003da∗x+b∗y+z

所以我们需要计算 aaa 和 bbb 。

这不能太难。我们已经知道笔画各部分中心的 x、y 和 z 坐标。在上面的图表中,它们的 x 和 y 坐标是蓝色的。我们分配给自己的 z 坐标。

在我们的例子中,我们希望 x 和 y 影响 z。所以剪切将平行于 z 轴。实际上,我们要剪切的轴是 p1p_1p1 和 p2p_2p2 之间的轴。

我们可以计算 aaa 和 bbb ,但我们也可以只围绕 z 轴旋转对象,这样我们想要剪切的轴就是 x 轴。

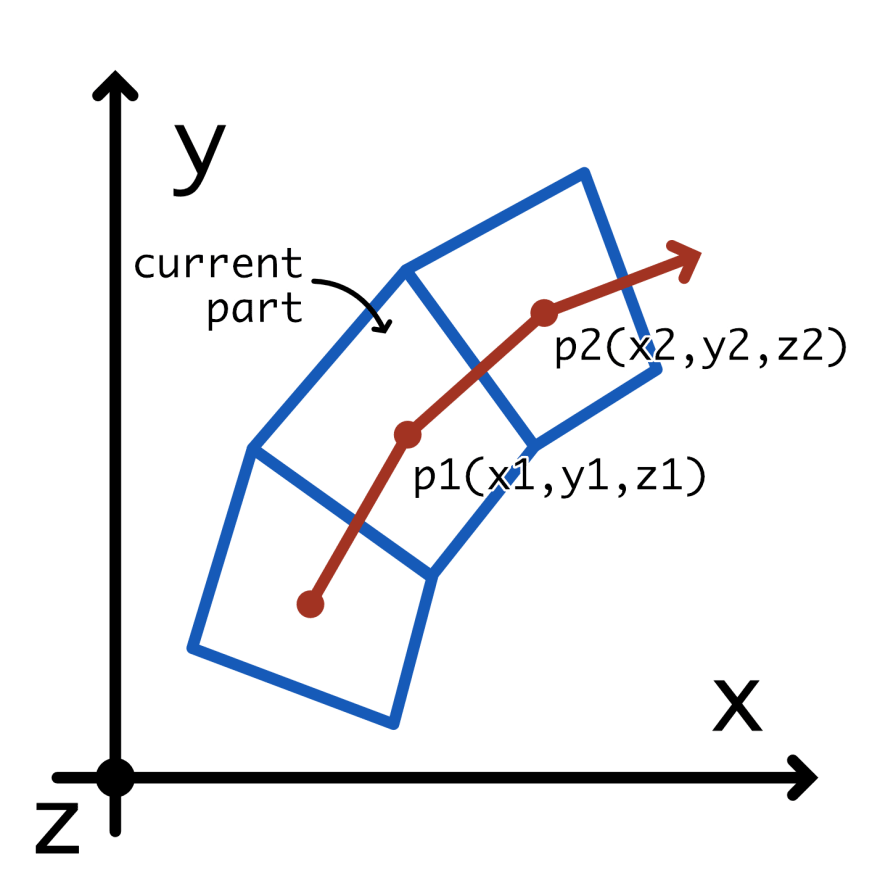
中风某些部分的顶视图

旋转矩阵如下所示:

[cos(θ)−sin(θ)00sin(θ)cos(θ)100001] \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 & 0\sin(\theta) & cos(\theta) & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \ end{bmatrix} ⎣⎡ cos(θ)sin(θ)00 −sin(θ )cos (θ)00 0010 0001 ⎦⎤

[](https://res.cloudinary.com/practicaldev/image/fetch/s--UHnxQE-B--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://dev-to- uploads.s3.amazonaws.com/uploads/articles/ms6ghui0fqo59nmcbg7r.png)

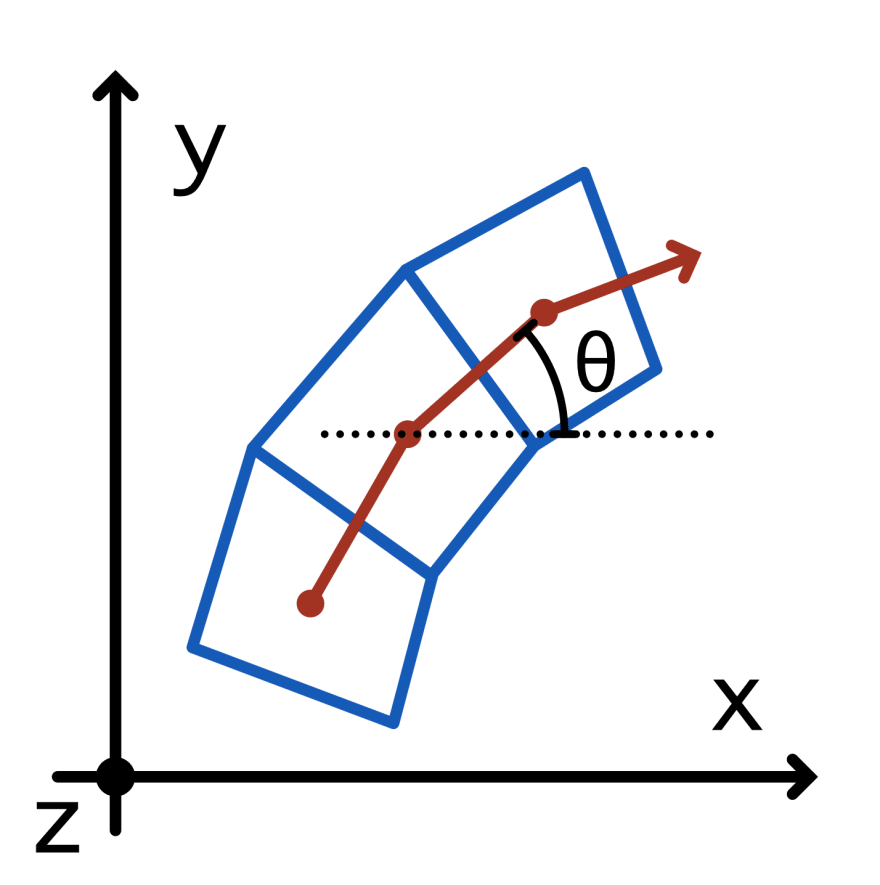
顶视图:我们需要将每个部分旋转 -θ 使其与 x 轴对齐

# calculate theta by using the arctangent
theta = np.arctan2(y2 - y1, x2 - x1)
# construct the rotation matrix, using -theta as the angle
rot_mat = np.matrix(
    (
        (cos(-theta), -sin(-theta), 0, 0),
        (sin(-theta), cos(-theta), 0, 0),
        (0, 0, 1, 0),
        (0, 0, 0, 1),
    )
).reshape((4, 4))

进入全屏模式 退出全屏模式

因为我们将剪切轴与 x 轴对齐,所以 b\u003d0b u003d 0b\u003d0 。剪切矩阵现在如下所示:

[# 00a100001] \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ a & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ⎣ ⎡10a1000100001⎦⎤

aaa 是 zzz 影响 xxx 的量。 ( x′\u003dx+a∗zx′ u003d x + a*zx′\u003dx+a∗z ) 所以我们可以推理:aaa 需要与笔画的斜率角度成正比。我们称这个角度为 α\alphaα 。

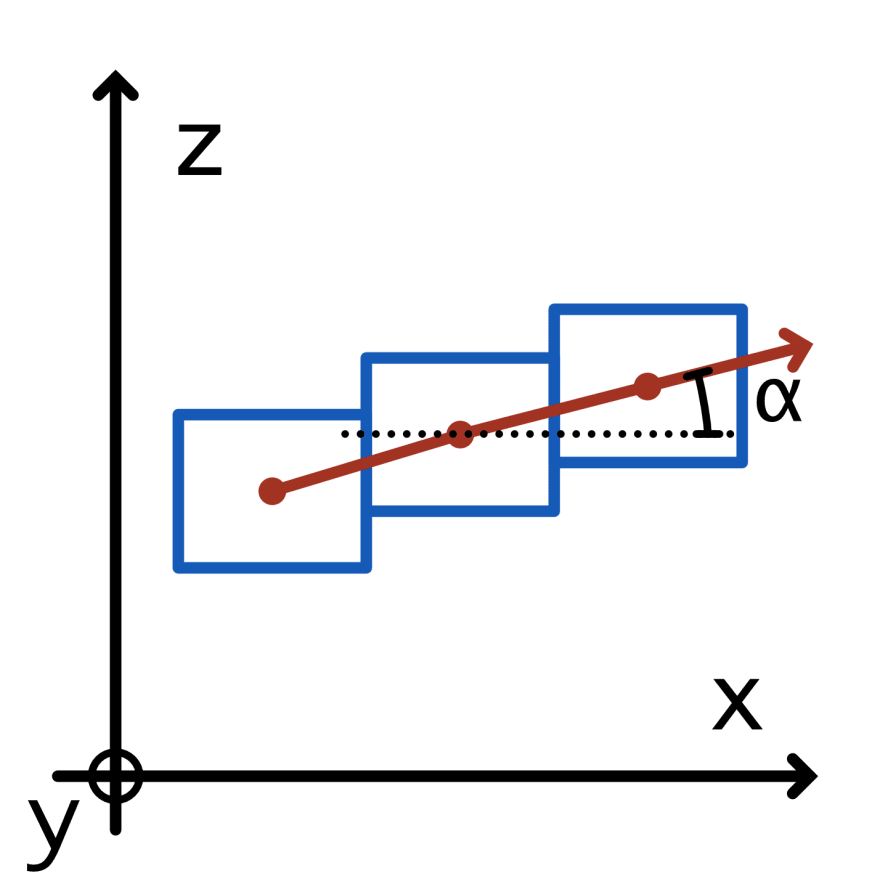
侧视图:我们需要将每个部分剪切 α

我们知道点的位置( p1p_1p1 和 p2p_2p2 ),所以我们可以计算切线如下:

距离xy\u003d(x2−x1)2+(y2−y1)2正切α\u003d(z2−z1)/距离xy 距离_{xy} u003d \sqrt{(x_2-x_1)^2 + (y\ _2-y_1)^2} \newline tangent_\alpha u003d (z_2-z_1) / distance_{xy} distancexy\u003d(x2−x1)2+(y2− y1)2正切α\u003d(z2−z1)/距离xy

distance_xy = sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)
tangent_alpha = (z2 - z1) / distance_xy

进入全屏模式 退出全屏模式

我们实际上不需要计算 α\alphaα !我们只需要 α\alphaα 的切线来构造剪切矩阵。这是有道理的,正切是 zzz 与 xxx 和 yyy 成比例的比率。

请记住 SOH-CAH-TOA:切线 u003d 对面/相邻。

[# 00tangentα100001] \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 正切_\alpha & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end {bmatrix} ⎣⎡10tangentα1000100001⎦⎤

shear_mat = np.matrix(
    (
        (1, 0, 0, 0),
        (0, 1, 0, 0),
        (tangent_alpha, 0, 1, 0),
        (0, 0, 0, 1)
    )
).reshape((4, 4))

进入全屏模式 退出全屏模式

现在我们知道了正确的剪切矩阵。

但是我们遗漏了一些重要的东西:我们的零件不在原点,所以剪切也会根据到原点的距离移动整个零件。为了解决这个问题,我们首先将零件移动到原点。

translate_mat = np.matrix(
    (
        (1, 0, 0, -x1),
        (0, 1, 0, -y1),
        (0, 0, 1, 0),
        (0, 0, 0, 1)
    )
).reshape((4, 4))

进入全屏模式 退出全屏模式

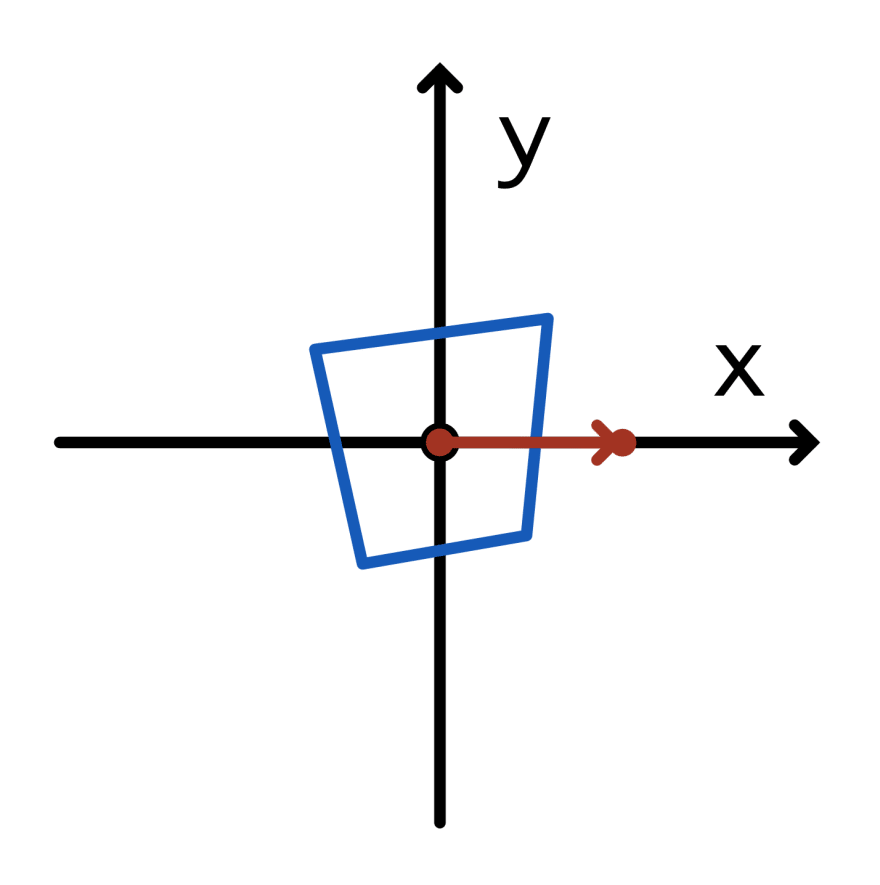
在原点旋转的零件的顶视图

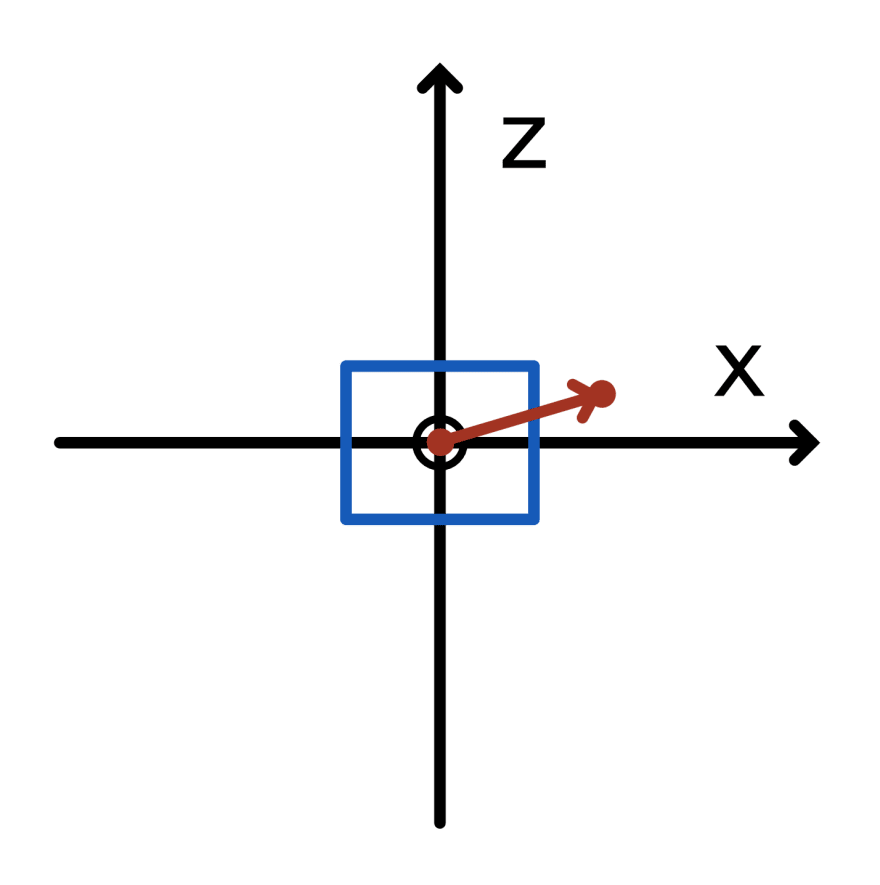
原点剪切前零件侧视图

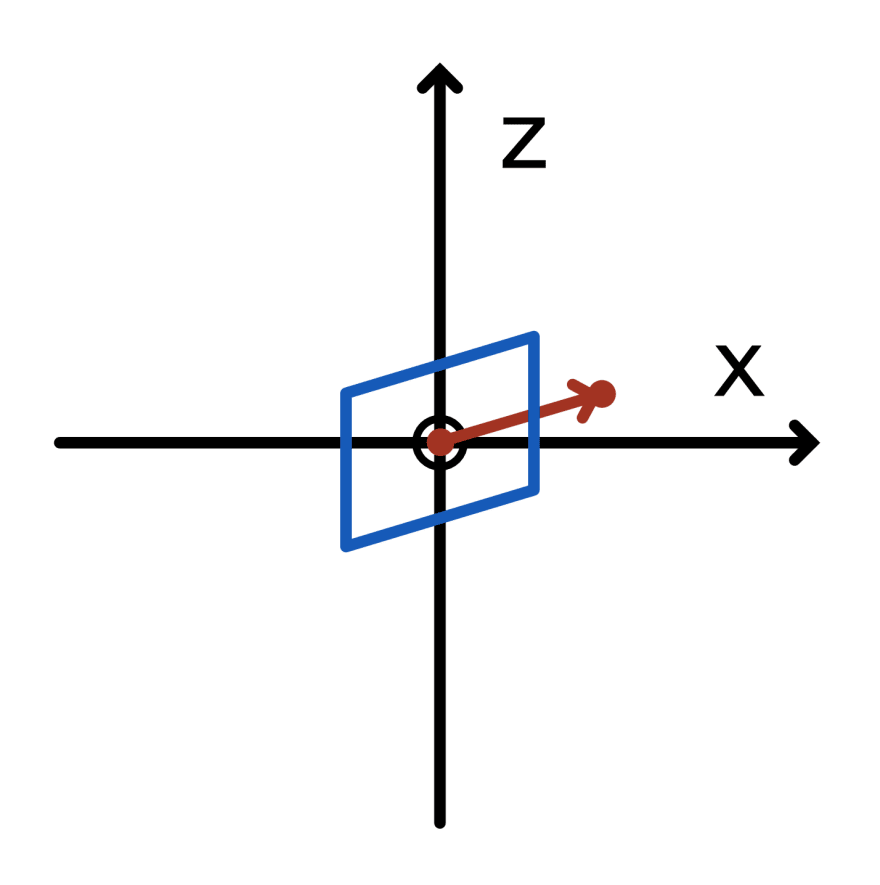
原点剪切后的零件侧视图

总的来说,矩阵将如下所示:

mat = np.identity(4)
# Apply translation
mat = np.matmul(translate_mat, mat)
# Apply rotation
mat = np.matmul(rot_mat, mat)
# Apply shear
mat = np.matmul(shear_mat, mat)
# Undo rotation
mat = np.matmul(np.linalg.inv(rot_mat), mat)
# Undo translation
mat = np.matmul(np.linalg.inv(translate_mat), mat)

total_obj += up(z)(multmatrix(np.asarray(mat))(obj))

进入全屏模式 退出全屏模式

我们最终会得到这样的结果:

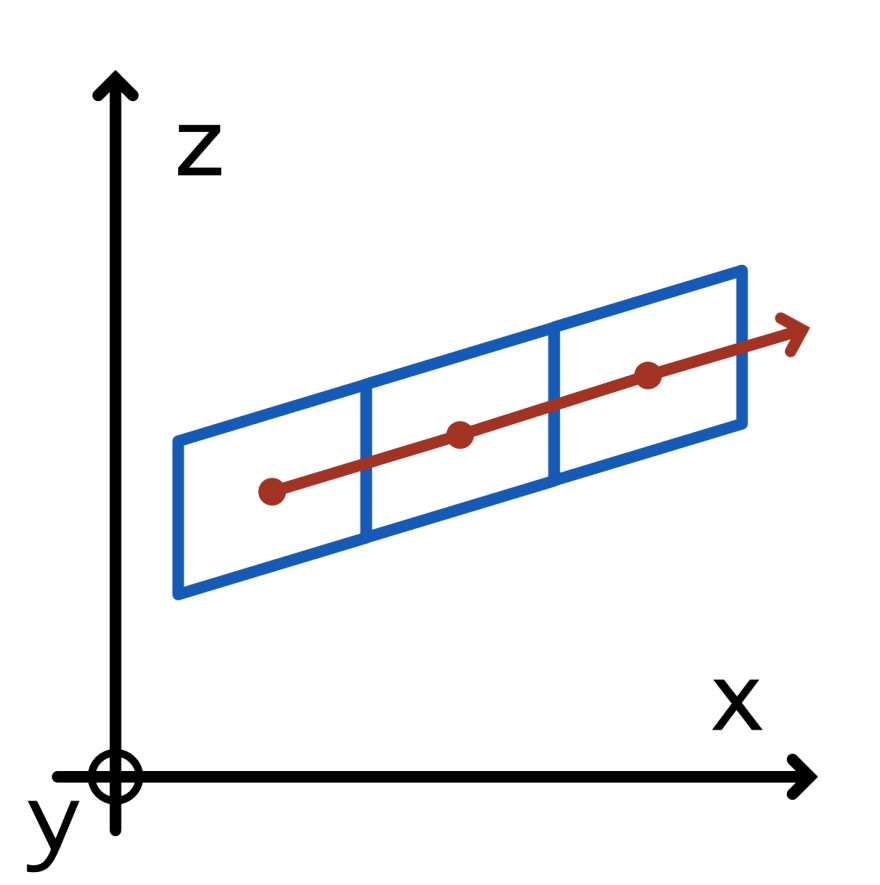
剪切的结果

非常好!

[](https://res.cloudinary.com/practicaldev/image/fetch/s--ghSvB4rA--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://dev- to-uploads.s3.amazonaws.com/uploads/articles/ruppunhycx2pfyp5fh3d.png)

动画剪切:

如您所见,拐角处和端点处的剪力还不理想。我通过用点平滑路径并采用剪切的移动平均值部分解决了这个问题。

平滑

如您所见,拐角处的平滑度不是很好。我认为使用这种分割方法不可能得到完美的平滑度,但我们可以做一些改进。

问题的部分原因在于中点创建了在角落处相当尖锐的 Voronoi 区域。中点的角越锐利,区域越锐利。

我添加了一种算法来消除这些角落的锐度。

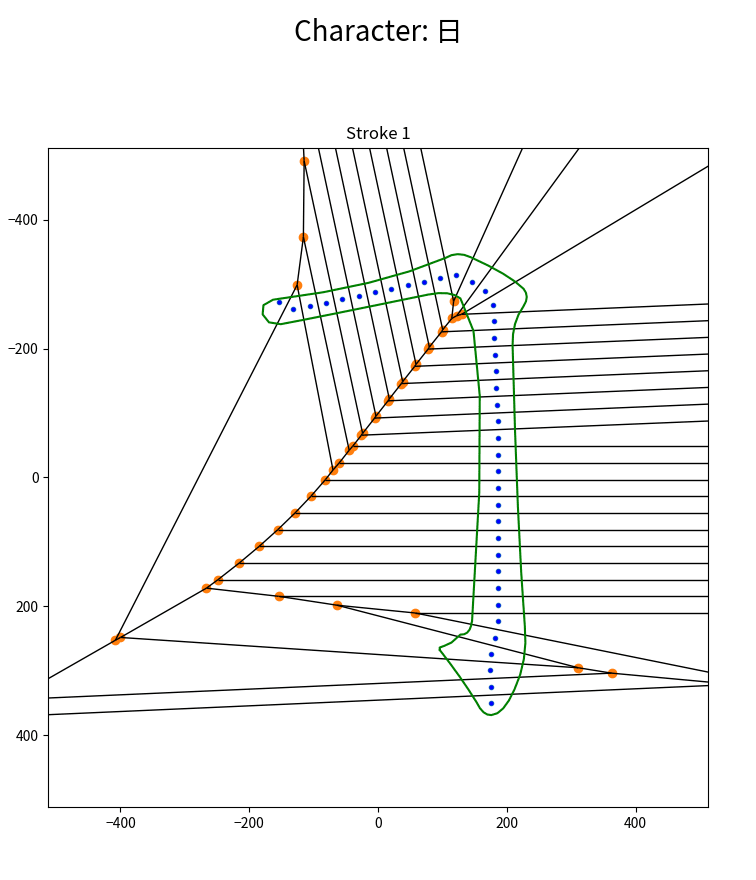
没有路径平滑的 Voronoi 区域

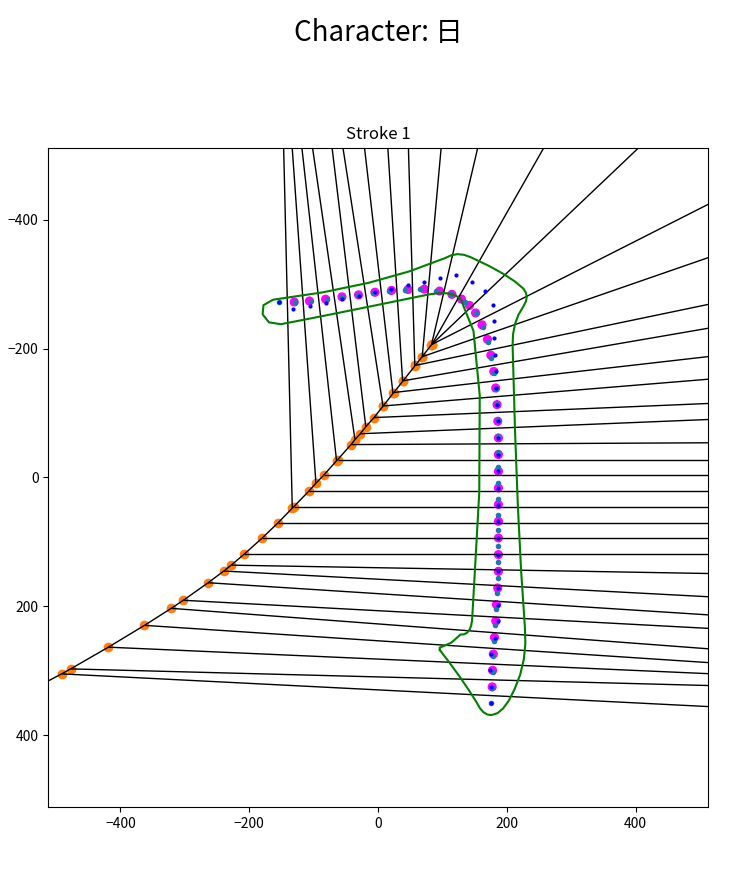
具有路径平滑的 Voronoi 区域

我不知道任何可以做到这一点的平滑算法,所以我发明了自己的:

[](https://res.cloudinary.com/practicaldev/image/fetch/s--XLKc6H-k--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://dev- to-uploads.s3.amazonaws.com/uploads/articles/zqwlw3jhtgtkhrf8ygt7.png)

• 创建一个空的输出点列表

• 将第一个输入点添加到输出点列表中

• 对于每 3 对输入点:

• 计算 3 点之间的角

• 计算角的平分角

• 在输出点列表中添加一个新点,要求:

• 点在二等分线上

• 点在拐角的内侧

• 角越尖,离输入点的距离就越大

• 将最后一个输入点添加到输出点列表中

• 重新插入点,使它们等距

重复这个算法 n 次。

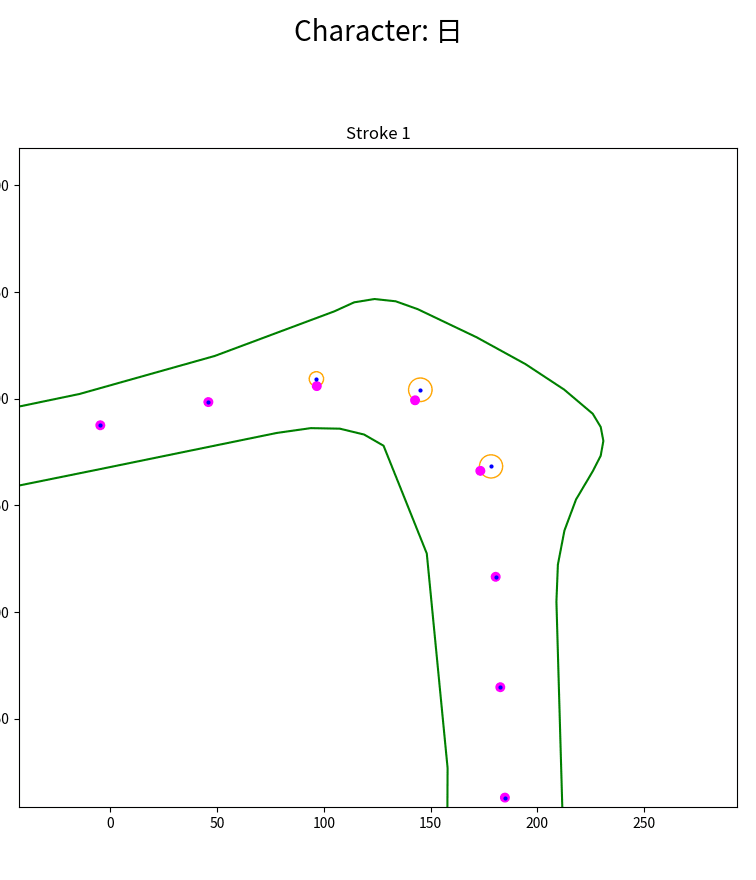
算法的第一次迭代。幅度为橙色,结果点为洋红色。

第一步:0 平滑步骤,最后一步:10 平滑步骤

第一步:0 平滑步骤,最后一步:15 平滑步骤

该算法收敛到一条直线。

我还添加了剪刀的移动平均线,这有助于更加平滑角落。

第一步:记住之前的 0 个部分,最后一步:记住之前的 10 个部分

两者都是对零件平滑度的显着改进,并产生了非常有用的零件 3D 模型。

这些功能还使我们能够不断增加零件数量,因为拐角问题现已得到解决。我们可以增加每个行程的零件数量并获得几乎光滑的表面!

最终结果

压扁零件

我们还可以添加一个模式来将每个笔划延伸到底部:

到底部模式

但是对于打印戒指或大部分是扁平的东西来说,这太高了。如果我们可以在将其拉伸到底部之前将其“压平”会更好。我们可以通过旋转顶部表面来实现这一点,使其或多或少是平坦的。

我把这个叫做untilted 模式。

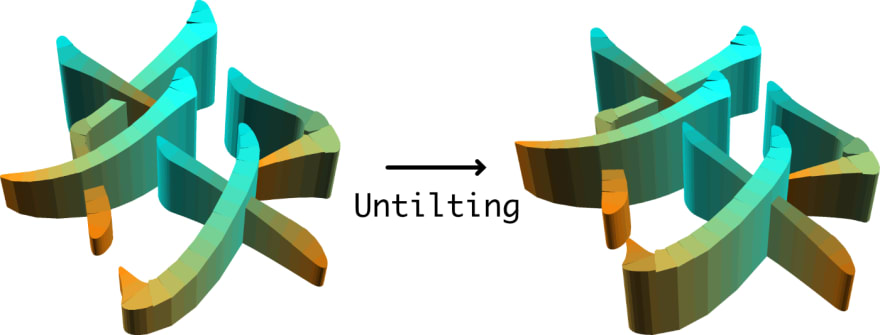[](https://res.cloudinary.com/practicaldev/image/fetch/s--O1rSb0eq--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://dev-to-uploads .s3.amazonaws.com/uploads/articles/r7k31ujoy5euklb3f4l5.png)

它通过对每个零件中心点的点云进行主成分分析来工作。然后,我们可以通过将 PCA 的特征向量与对象进行矩阵相乘来消除倾斜。

例如:

from sklearn.decomposition import PCA

pca = PCA()
pca.fit(medians_3d)
eigenvectors = pca.components_

mat = [(*values, 0) for values in eigenvectors] # pad with 0

obj = multmatrix(mat)(obj)

进入全屏模式 退出全屏模式

如果我们只是运行它,我们可以看到顶部是平的,正如我们想要的那样。但是角色也会旋转和倾斜。

[之前](https://res.cloudinary.com/practicaldev/image/fetch/s--K9r0_SMP--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://dev-to- uploads.s3.amazonaws.com/uploads/articles/o1tfxk42xlb84yy8xuk2.png)

拧开前的无标题模式

我们需要添加一些额外的代码来强制转换保持垂直线垂直。

# make sure z doesnt have an effect on x and y
eigenvectors[0][2] = 0
eigenvectors[1][2] = 0

进入全屏模式 退出全屏模式

由于某种我不确定的原因,特征向量也可能被反转。

# make sure all eigenvectors are in the same direction as the current axis
for i in range(3):
    # e.g. for Z, if 0, 0, 1 would map to *, *, < 0, then invert it
    if eigenvectors[i][i] < 0:
        eigenvectors[i] = -eigenvectors[i]

进入全屏模式 退出全屏模式

我们还需要消除可能围绕 z 轴的旋转和 xy 平面的缩放。

# make sure there's no rotation around z or scaling of the xy plane
eigenvectors[0][0] = 1
eigenvectors[0][1] = 0
eigenvectors[1][0] = 0
eigenvectors[1][1] = 1

进入全屏模式 退出全屏模式

在这些检查之后,字符就是我们想要的:

[](https://res.cloudinary.com/practicaldev/image/fetch/s--aGQqwq5u--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://dev-to- uploads.s3.amazonaws.com/uploads/articles/6qoo4b6fqioijj2ss1i5.png)

未来

我认为应该可以通过转换网格上的晶格来生成完美光滑的表面。这可能通过某种 Blender 插件实现。我认为甚至可以重用平滑算法,是否可以使用 Voronoi 图还有待观察。目前,这个简单的脚本可以满足大多数 3D 打印需求。

OpenSCAD 渲染和渲染到 STL 也是一个瓶颈。我认为应该可以将其移植到带有参数滑块的基于 Web 的应用程序,这样您就可以获得即时反馈,而不必等待渲染。

使用 OpenJSCAD 将其移植到 Javascript,或者移植到编译语言,然后移植到 WebAssembly 也是一种可能。

有兴趣吗?

如果您想尝试生成自己的部分,请查看repo,如果您有任何想法或建议,请打开问题或在Twitter上向我发送消息。

hansottowirtz/3d-汉字生成器

按照笔画顺序创建汉字/汉字的3d模型和STL

zd汉字发电机

简介

该程序使用来自Make me a Hanzi的笔画数据生成一个汉字/汉字字符的 3d 模型。它以笔画顺序作为 Z 维度来拉伸字符。

它通过按照笔划顺序将每个笔划拆分为多个部分,然后将每个部分倾斜以形成一个斜率来实现这一点。

在这篇博客文章中,我将详细介绍该程序的内部工作原理。它使用 Solid Python、OpenSCAD、Voronoi 图、PCA 和相当多的线性代数。

个例子

观看这个 YouTube 视频查看一些示例。

用途

程序的输入是一个 .yml 文件,其中包含生成模型的设置。

python src/main.py --out-scad main.scad --stl true --out-stl main.stl --settings examples/ai.yml --parts strokes

进入全屏模式 退出全屏模式

有关所有配置选项,请参见src/base_settings.yml。

安装

创建一个 venv 或类似的,然后:

pip3 install -r requirements.txt

进入全屏模式 退出全屏模式

在 ARM macOS 上安装

由于...

在 GitHub 上查看