第3章 运算方法和运算器
摘要:本文详细介绍了C语言中的移位运算,包括逻辑移位和算术移位。逻辑移位针对无符号数,左移高位移除低位补0,右移低位移除高位补0;算术移位针对有符号数,保持符号位不变,数值位移位。文章还阐述了不同编码方式(原码、反码、补码)下的空位添补规则,并说明了移位运算在寄存器位操作和乘法运算中的应用场景。最后介绍了补码的特殊算术移位方式及其优点。
1、移位运算
1)逻辑移位
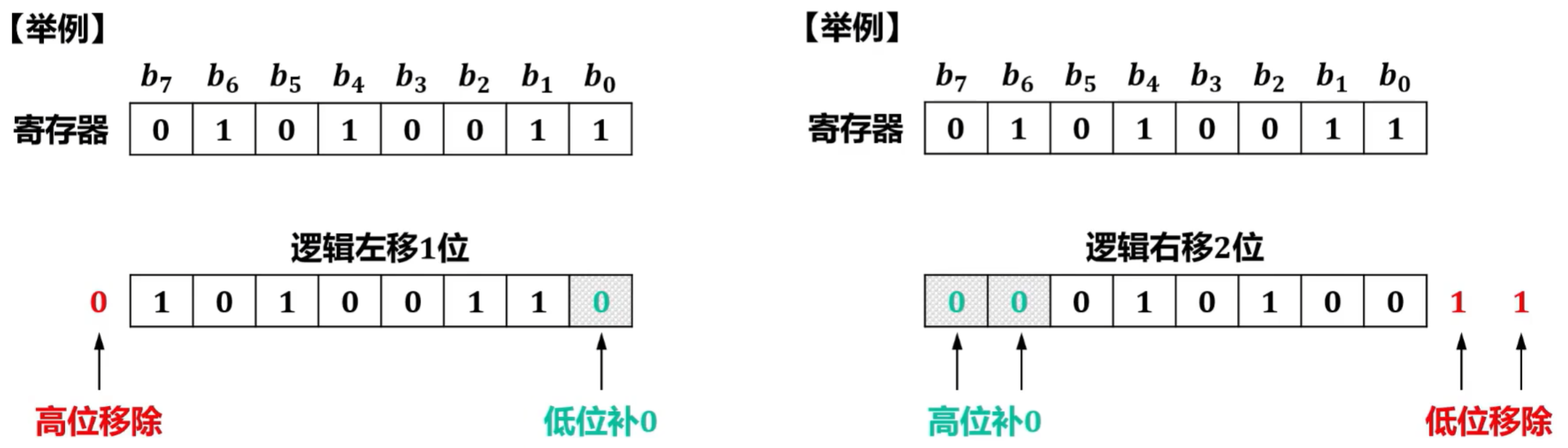
- C语言中的移位运算操作符包括“ << ”和“ >> ”两种,分别表示左移和右移
- 左移运算操作符“ << ”,对应汇编指令中的逻辑左移,即高位移除,低位补0;
- 右移运算操作符“ >> ",则根据操作数是无符号还是有符号类型分别对应汇编指令中的逻辑右移和算术右移指令;
- 逻辑右移:将低位移除,高位补0;
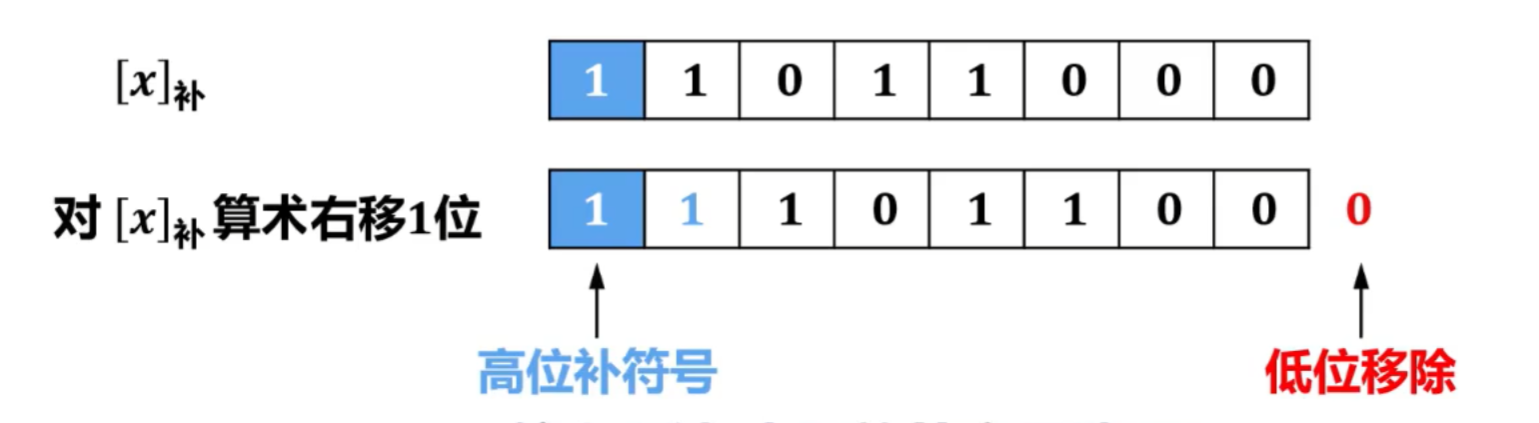
- 算术右移:将低位移除,高位补原数据的符号位。
①基本概念
-
逻辑移位的对象:无符号数
-
逻辑移位的规则:
-
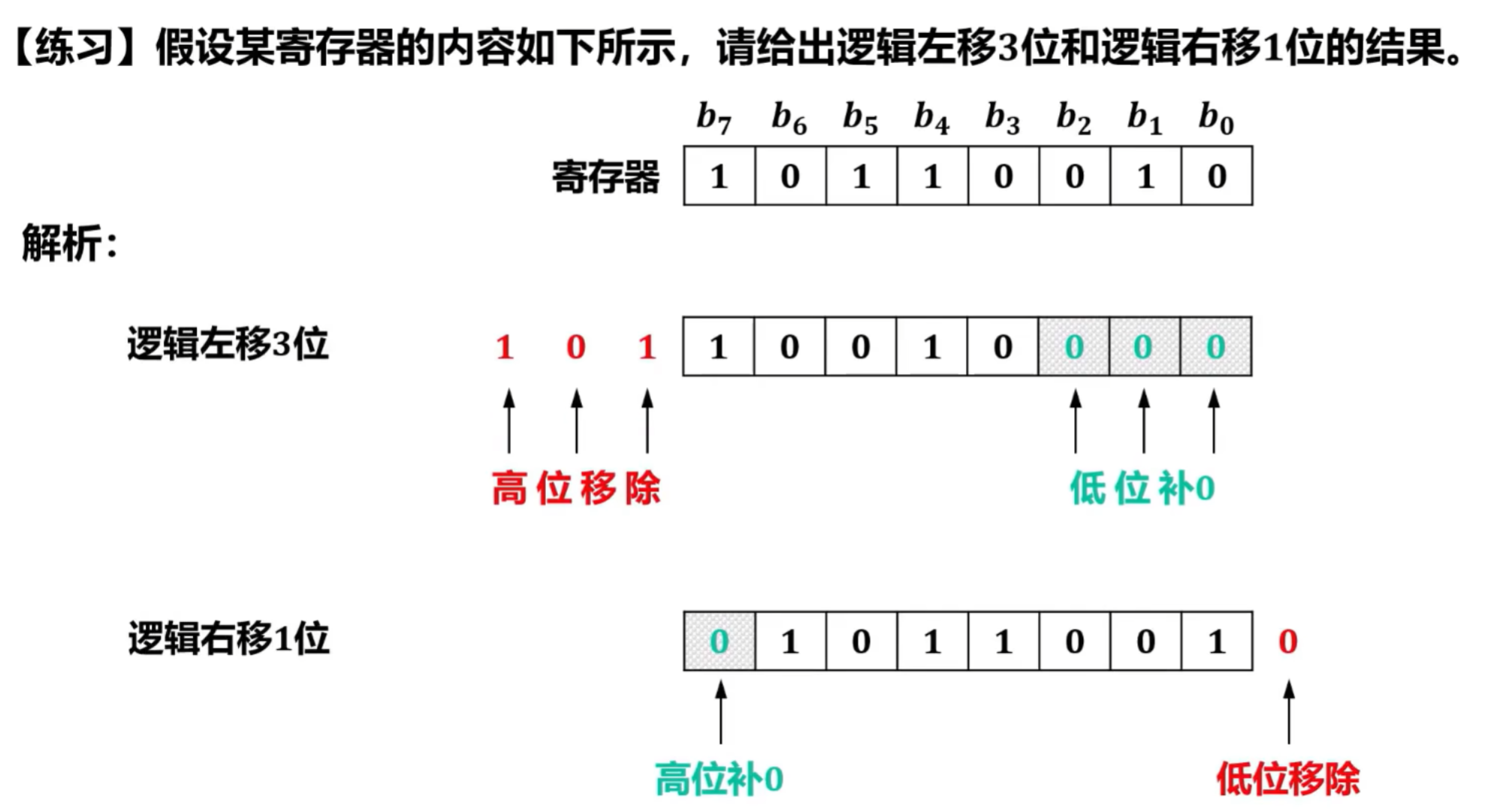
逻辑左移:高位移除,低位补0;
-
逻辑右移:低位移除,高位补0。
-
②应用场景
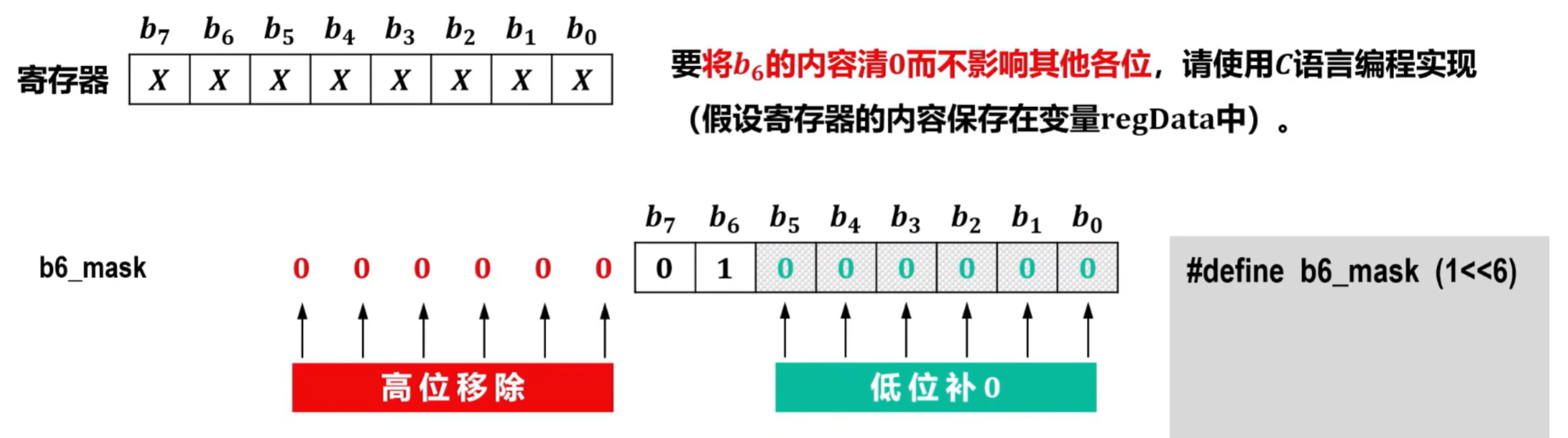
利用逻辑移位运算、取反运算、与/或运算实现寄存器中某个位清0或置1,不影响其他各位
-
定义宏,将数值1的二进制左移6位,得到以下结果:
-
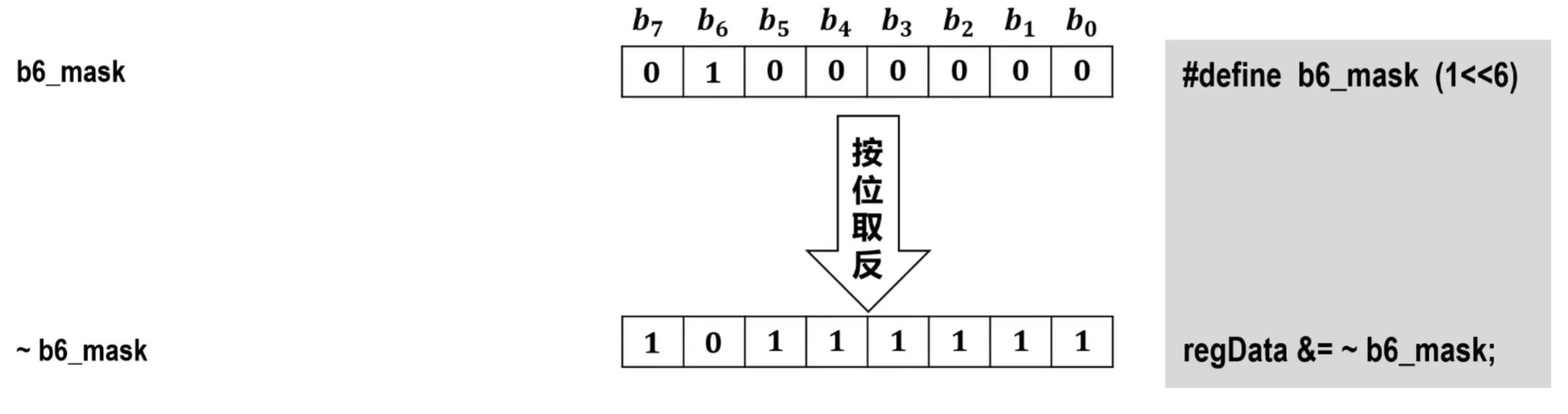
将b6的掩码按位取反得到以下结果:
-
进行与运算
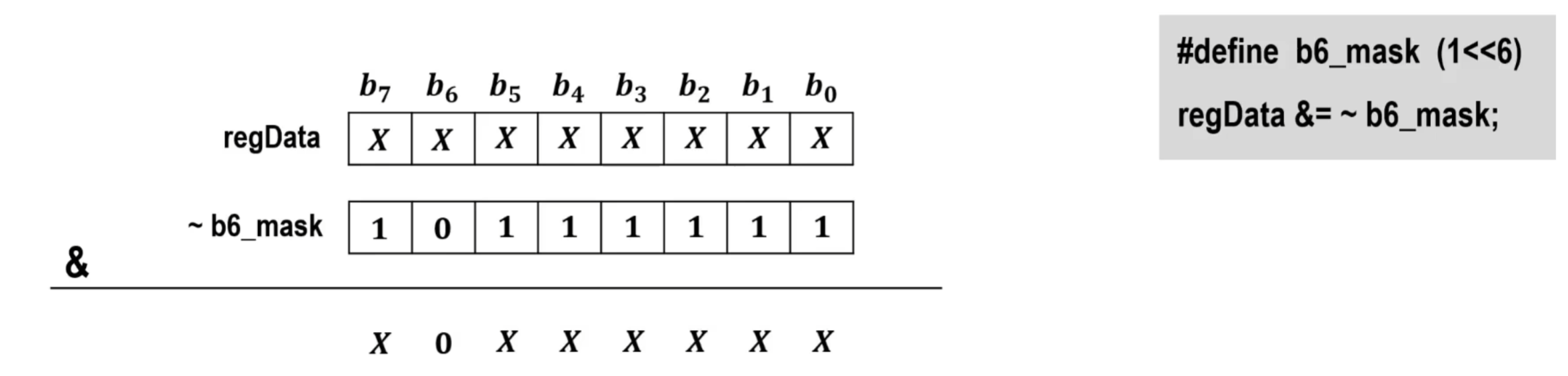
-
写回regData
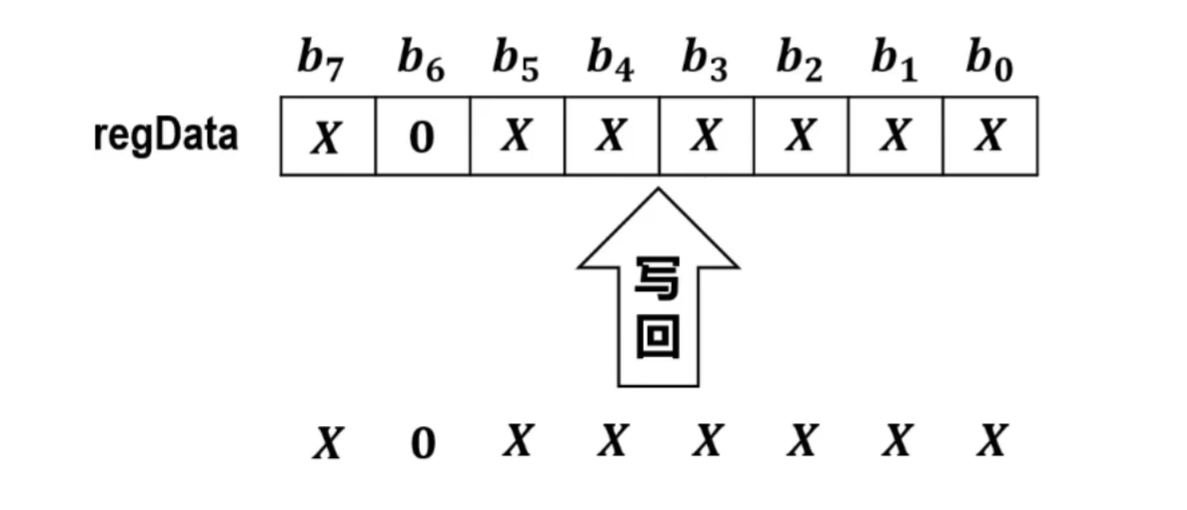
如果要将b6的内容置为1,只需要将与运算换成或运算即可

2)算术移位
①基本概念
- 逻辑移位的对象:有符号数(针对定点数,包括定点整数和定点小数);
- 不论正数还是负数,符号位保持不变,仅对数值位进行移位(左移或右移);
- 对真值的原码、反码和补码进行算术移位后,它们各自所对应的新的真值应该保持一致;
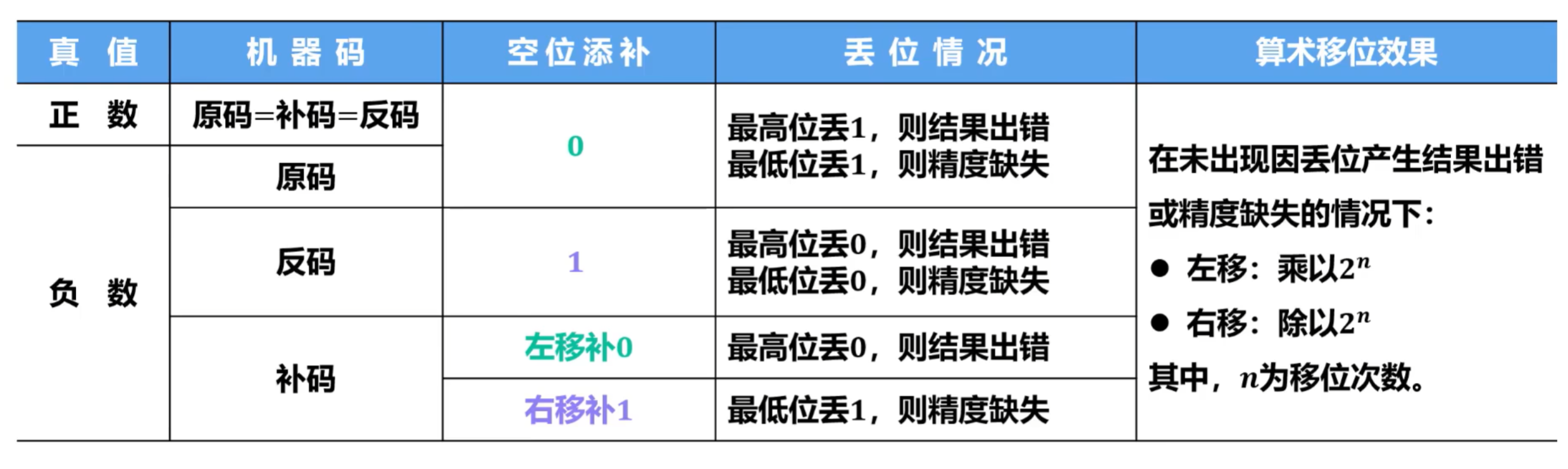
- 当真值为正数时,真值的原码,反码和补码都相同,因此,对它们进行算术移位后,它们各自所对应的新的真值自然是保持·致的。对于移位后出现的空位,规定添补0;
- 当真值为负数时,真值的原码、反码和补码都不同,因此,对它们进行算术移位后,为了确保它们各自所对应的新的真值保持一致,对于移位后出现的空位,添补规则各不相同。
②空位的添补规则
- 对于真值为正数左移情况
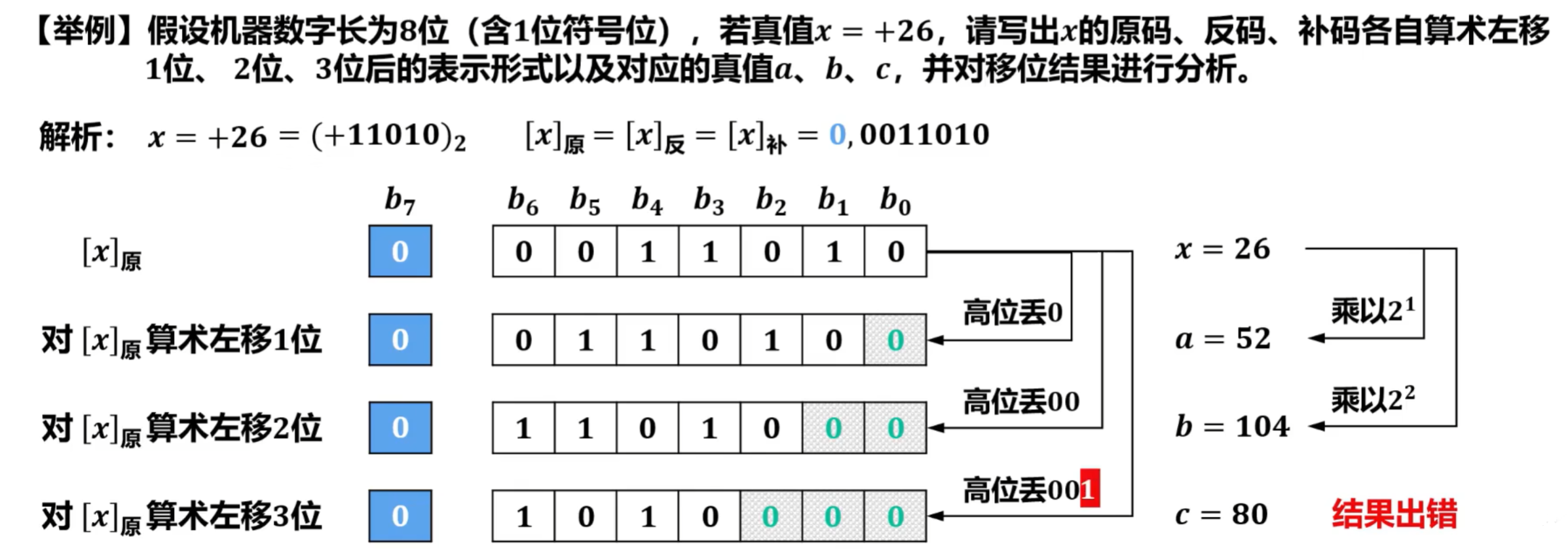
- 对于真值为正数右移情况
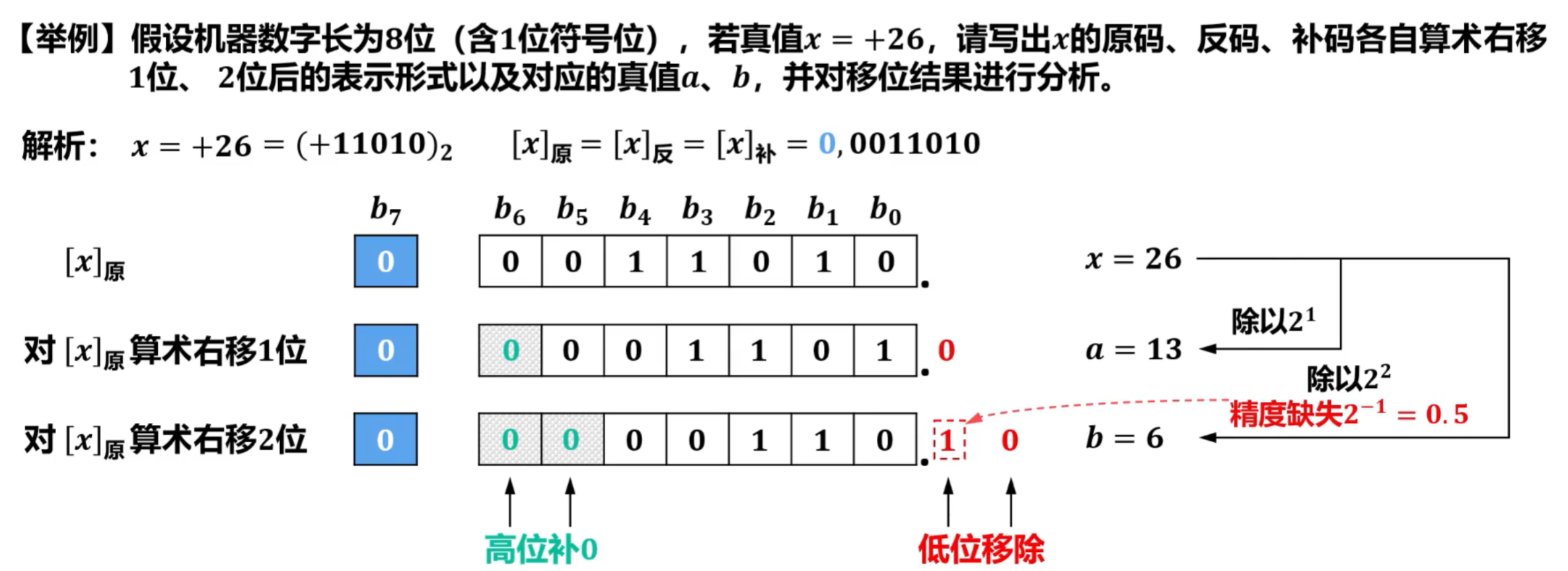
- 对于真值为负数,真值的原码、反码和补码规则不同
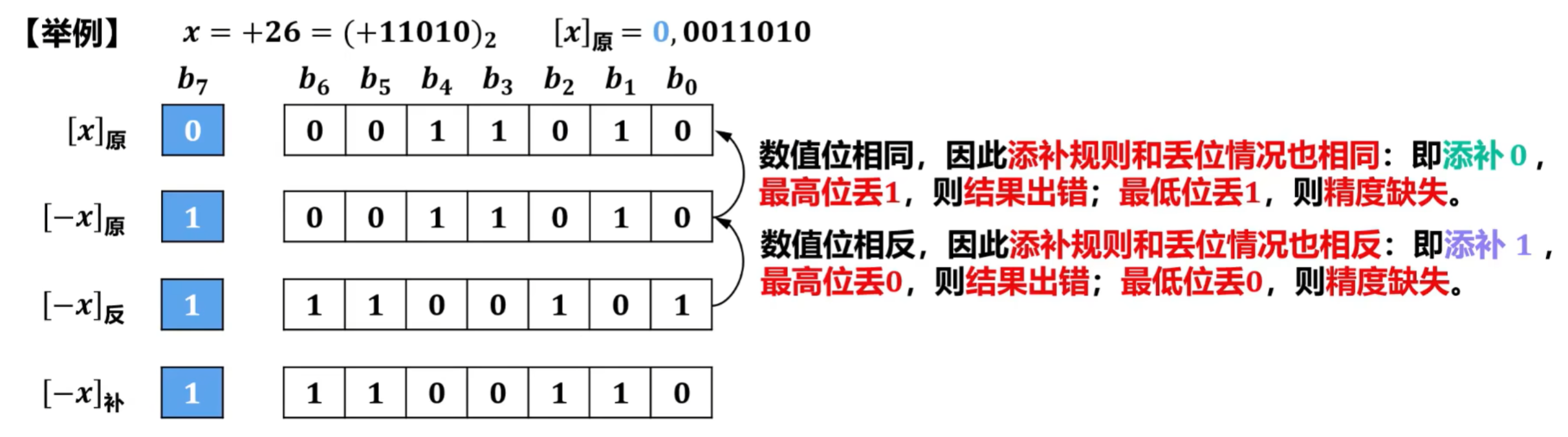
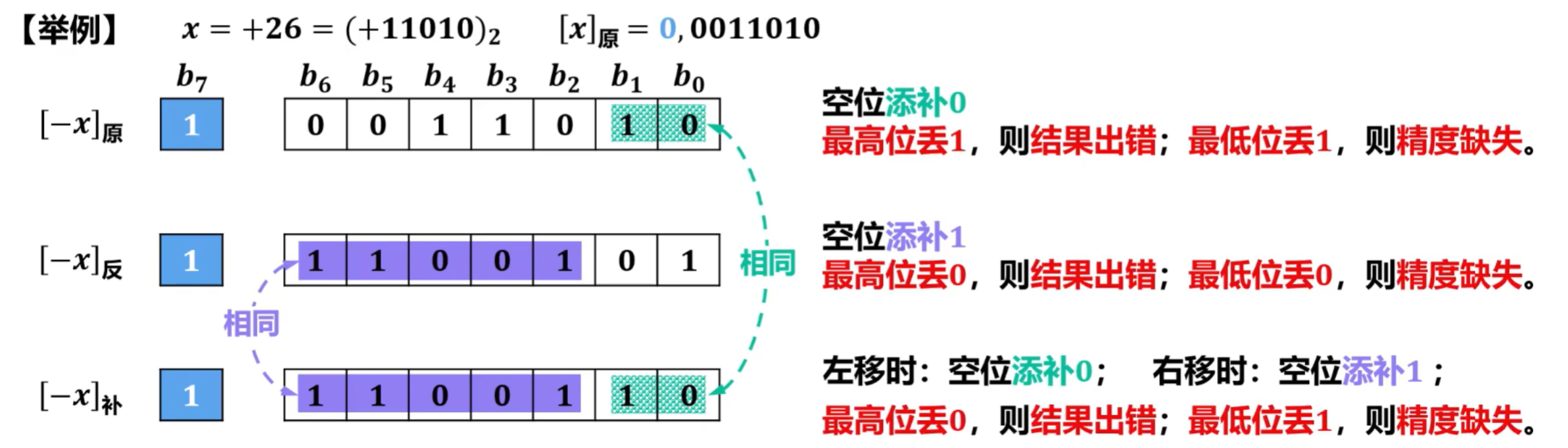
- 总结如下:
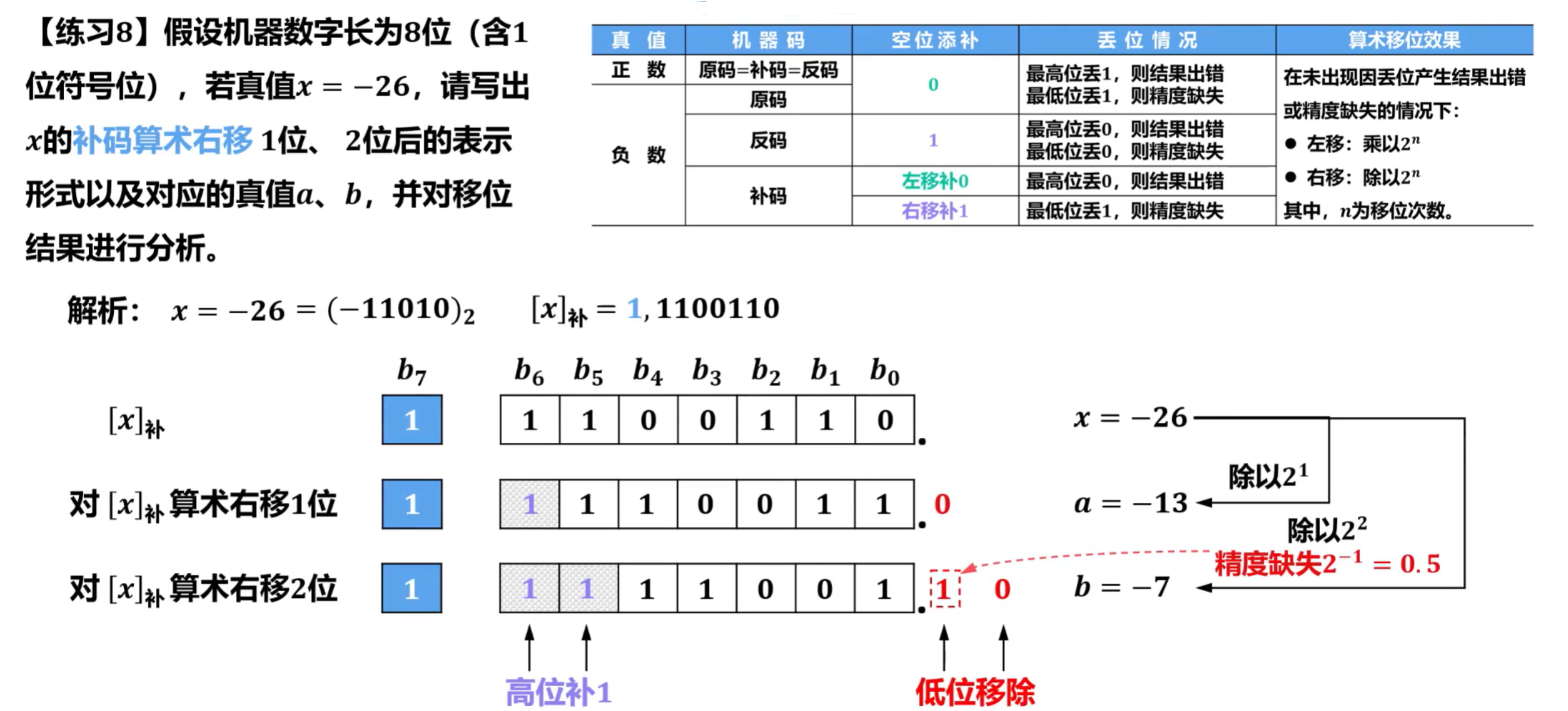
例题:
对原码进行左移
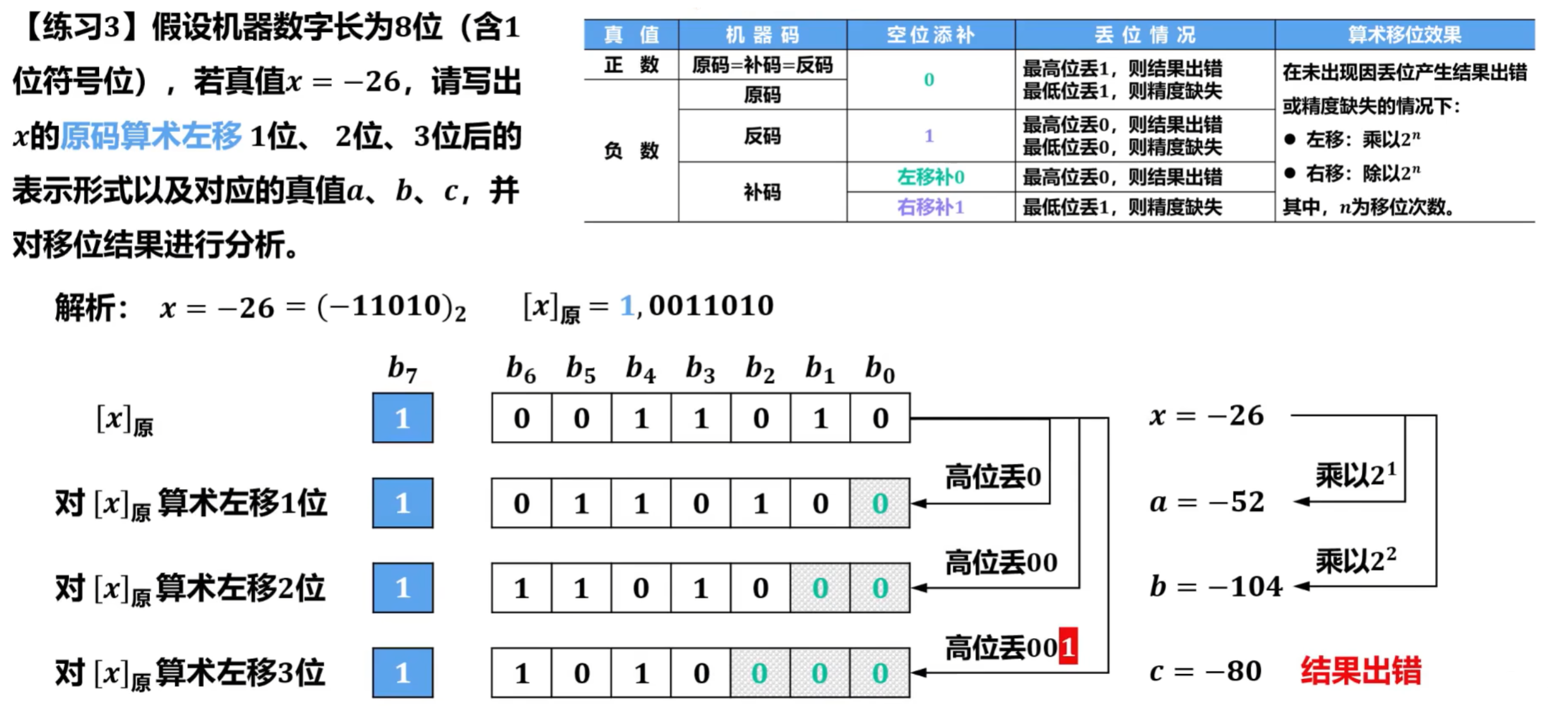
对反码进行左移
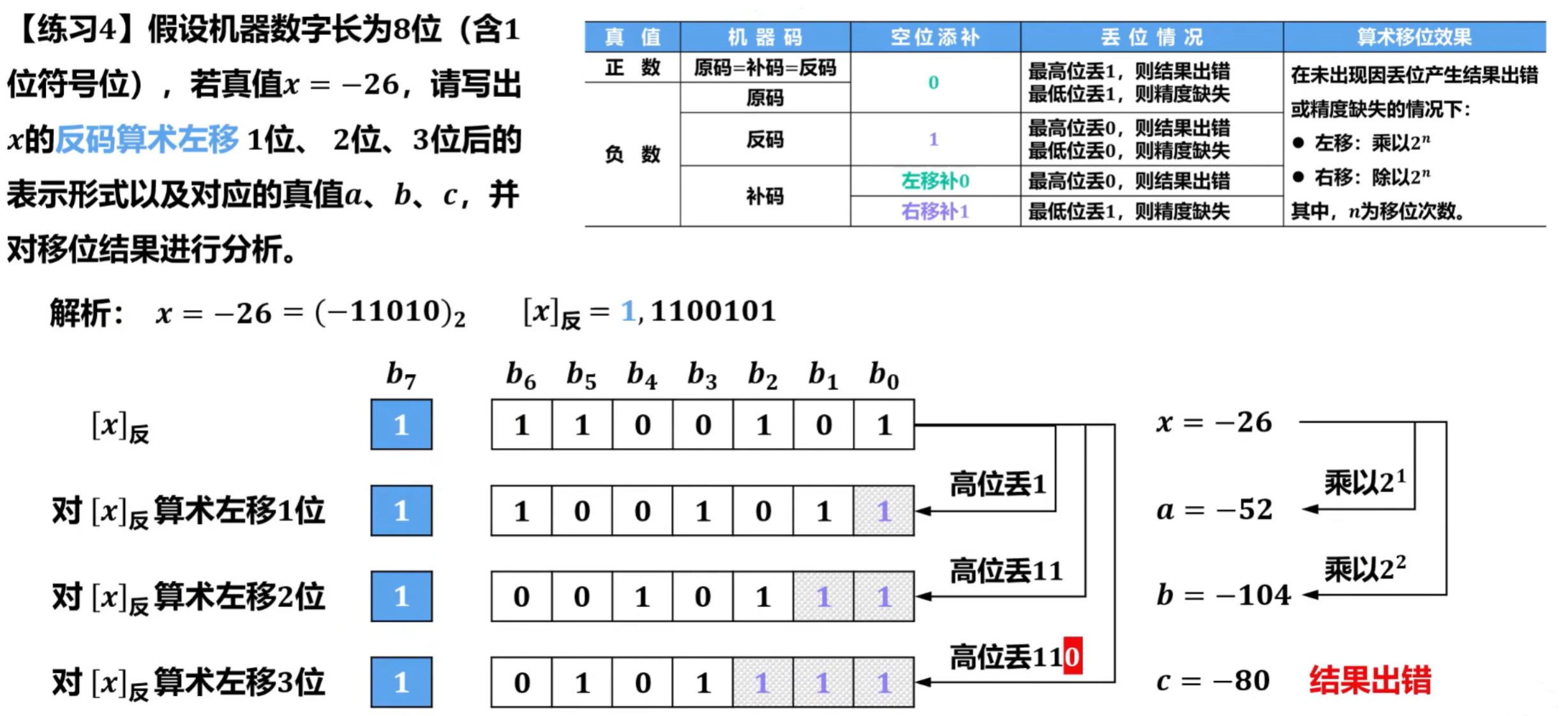
对补码进行左移
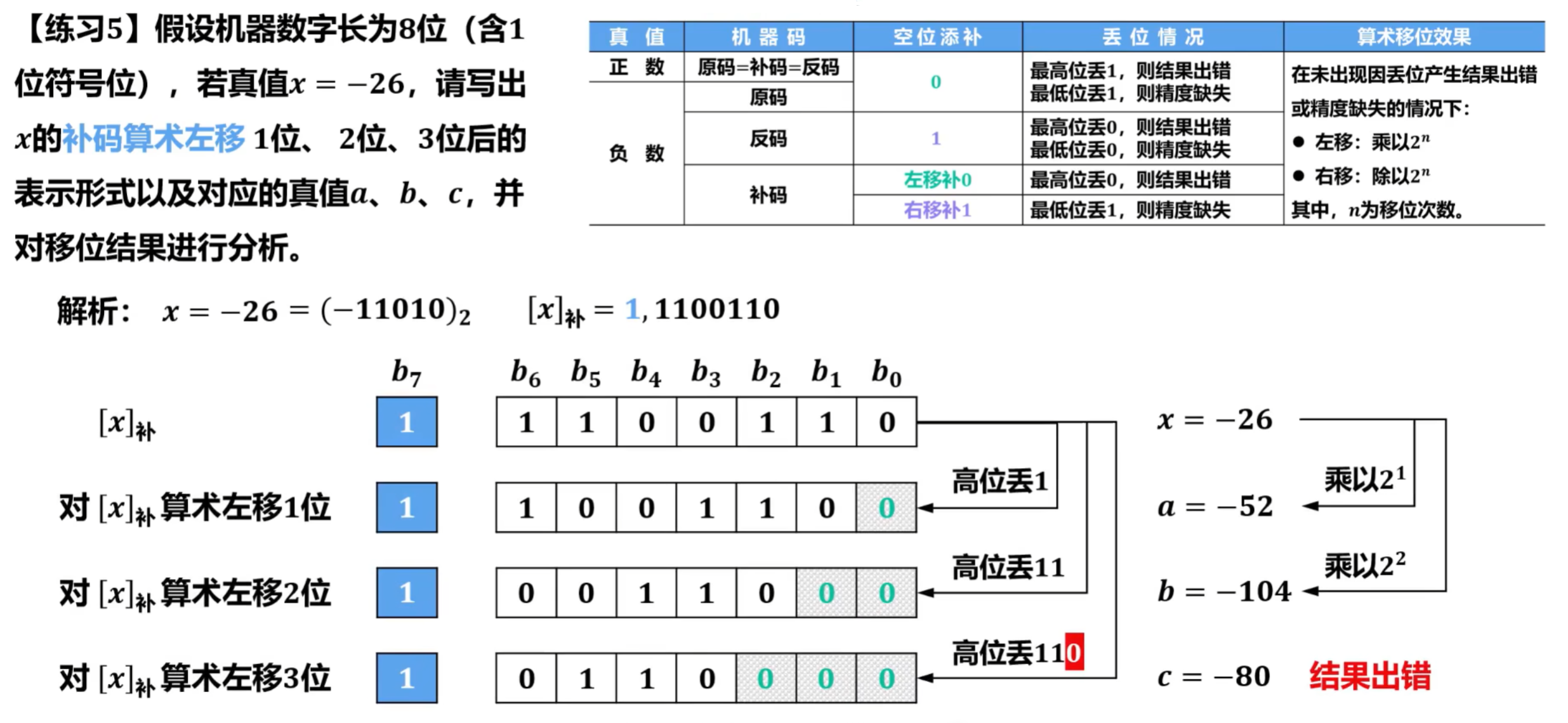
对原码进行右移
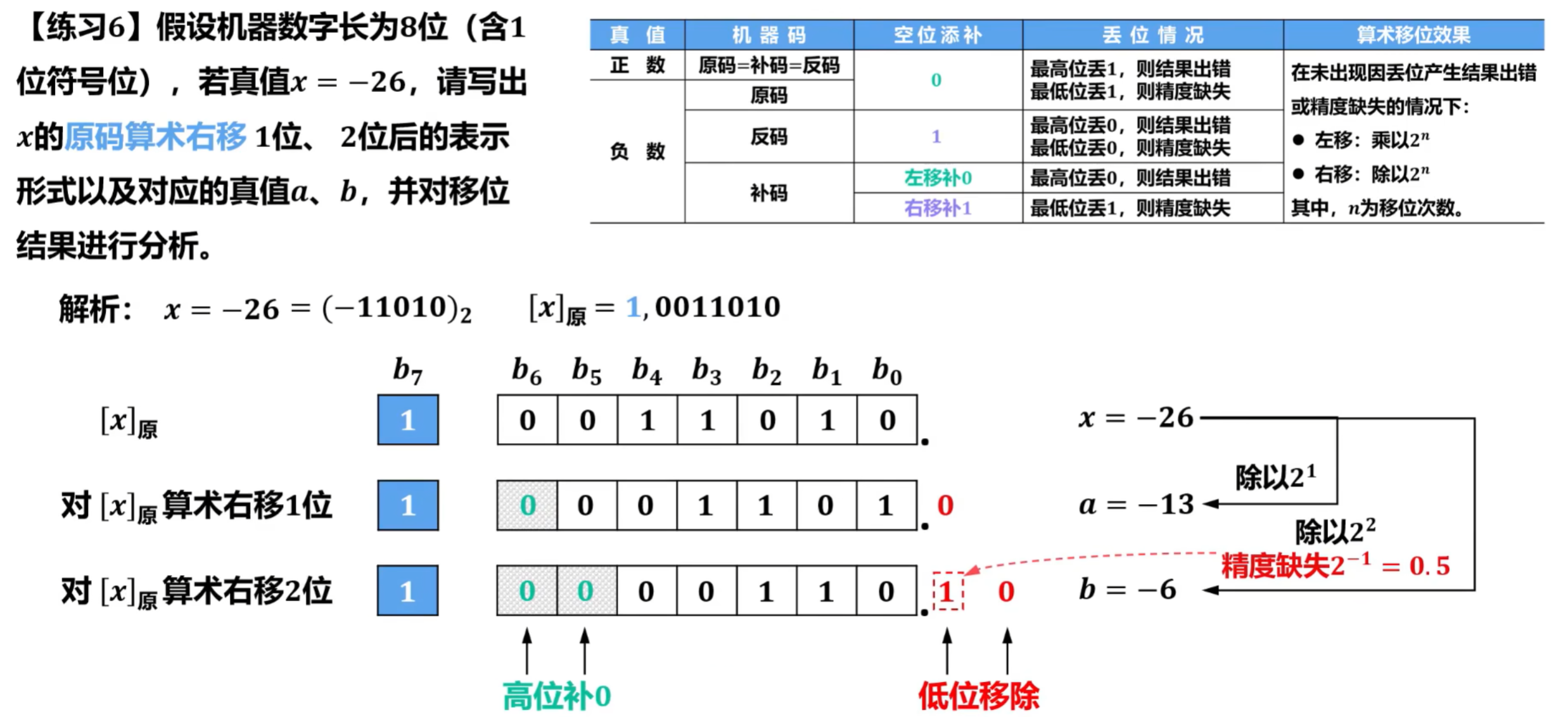
对反码进行右移
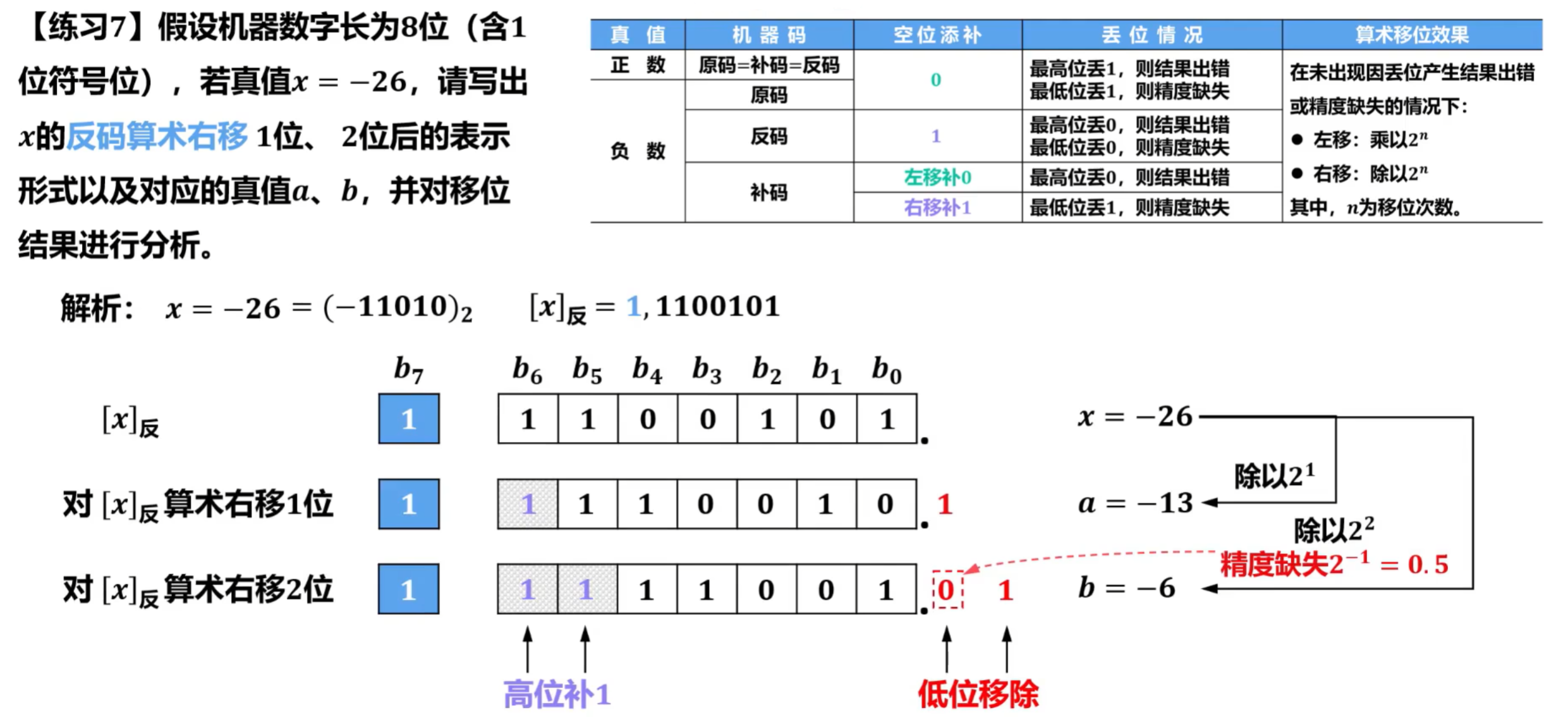
对补码进行右移
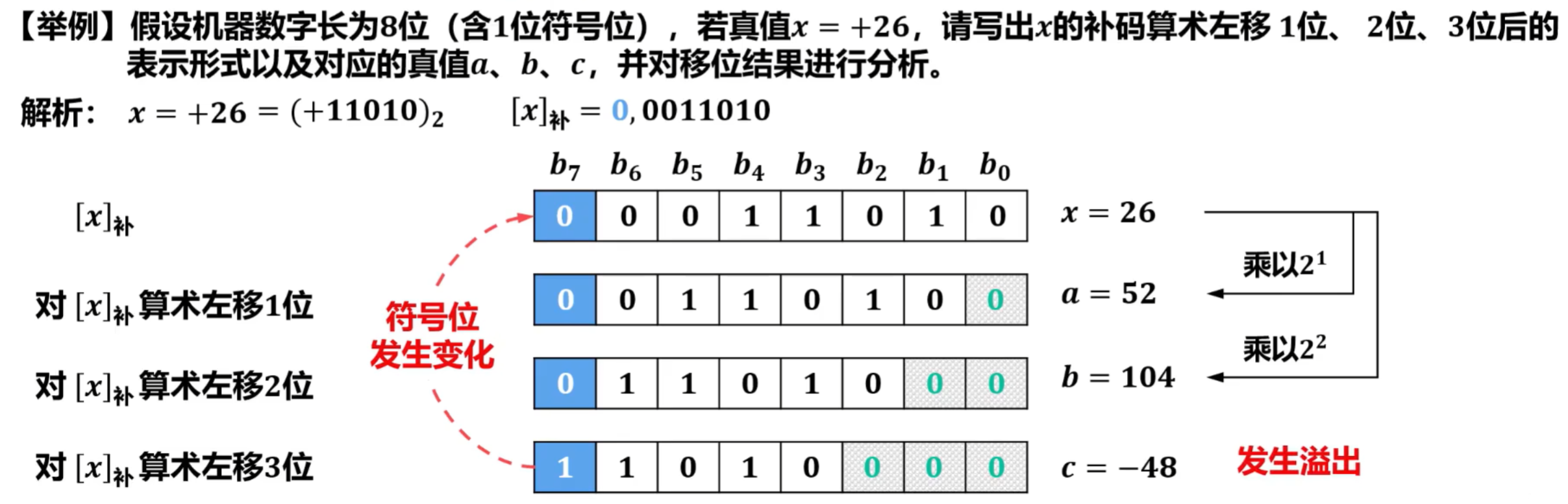
③补码的特殊算术移位
- 有符号定点数的补码的另一种算术移位方法,即“ 符号位也参与移位 ”
- 具体规则如下:
- 左移:高位移除,低位添补0;移动前后若符号位发生变化,则发生溢出;
- 右移:低位移除,高位添补符号。
左移
右移
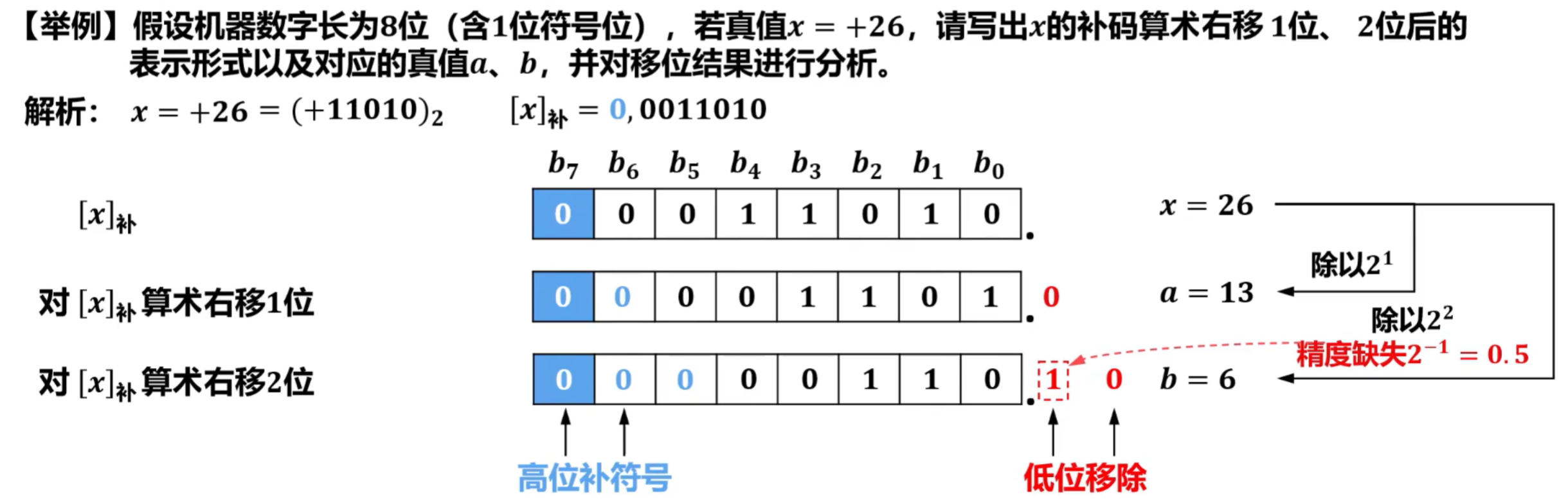
优点:
左移时,有检测出发生溢出的方法:符号位发生变化可判定溢出;
符号位与数值位一起移位,方便ALU处理,也方便人们记忆
④应用场景
计算机中的乘法运算可用加法和算术移位操作得到
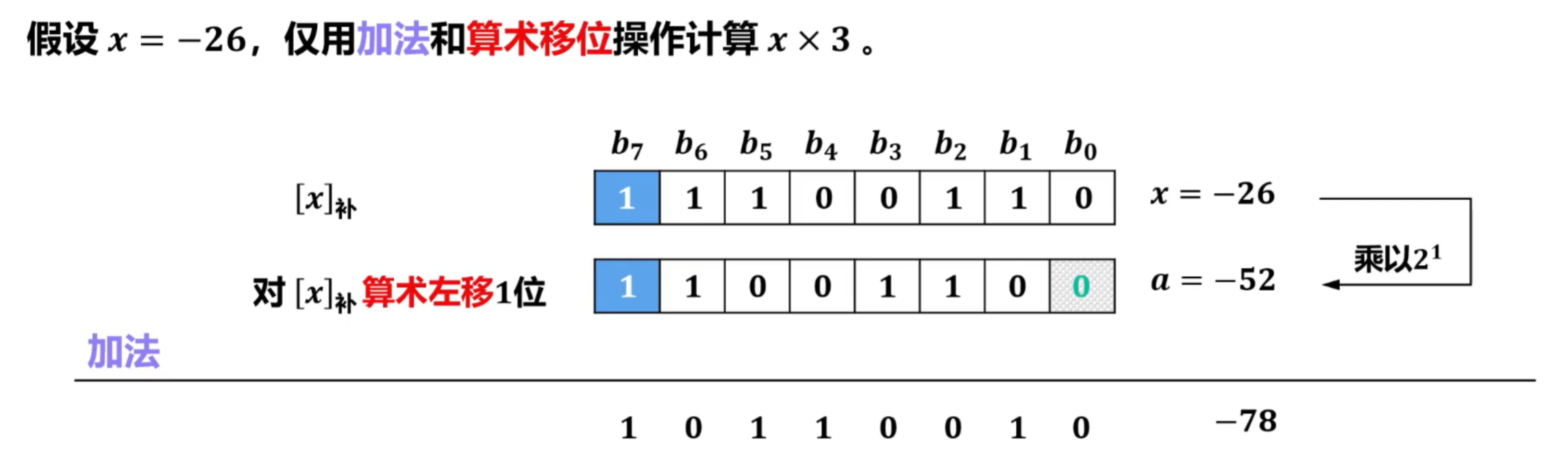
例题:

3)循环移位
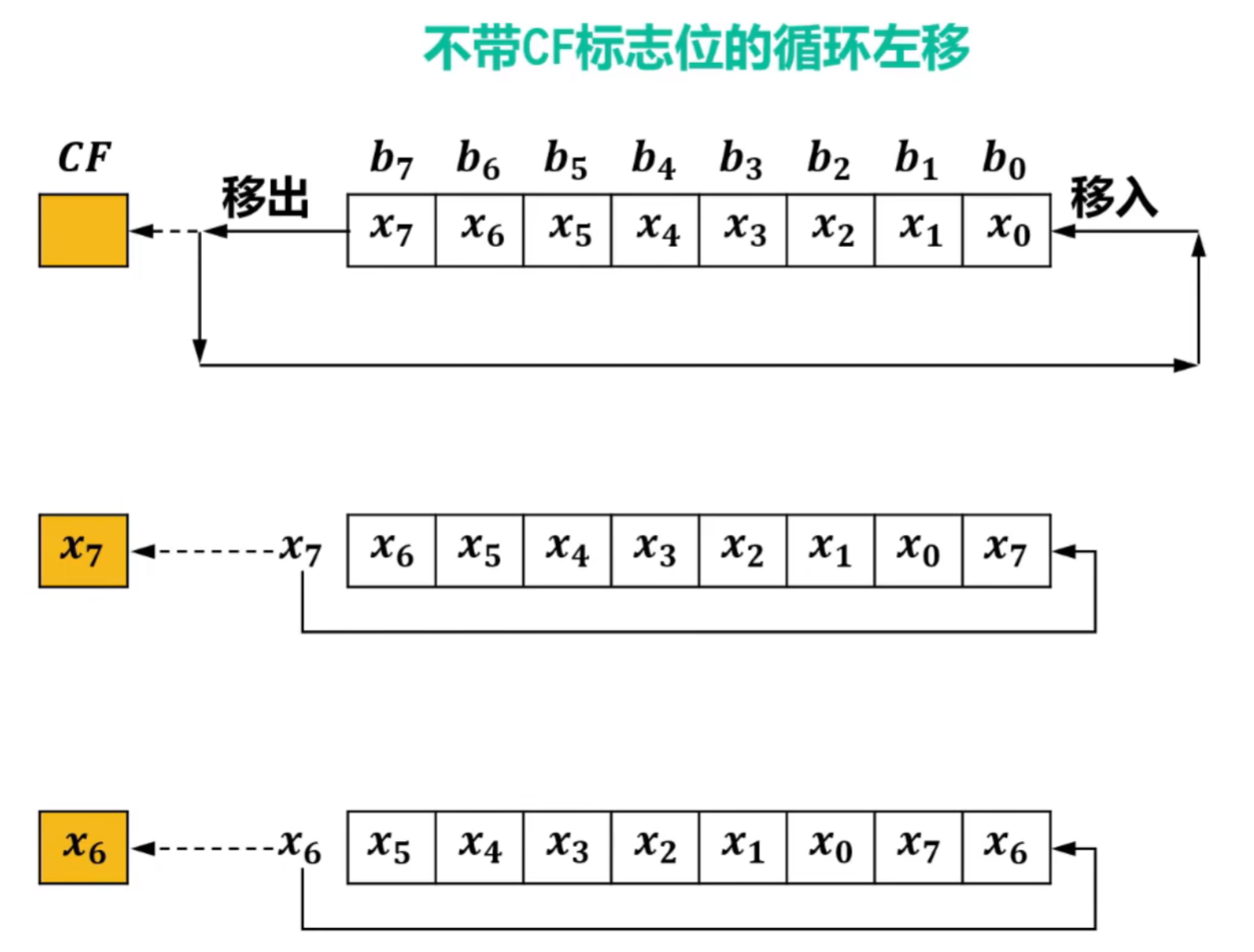
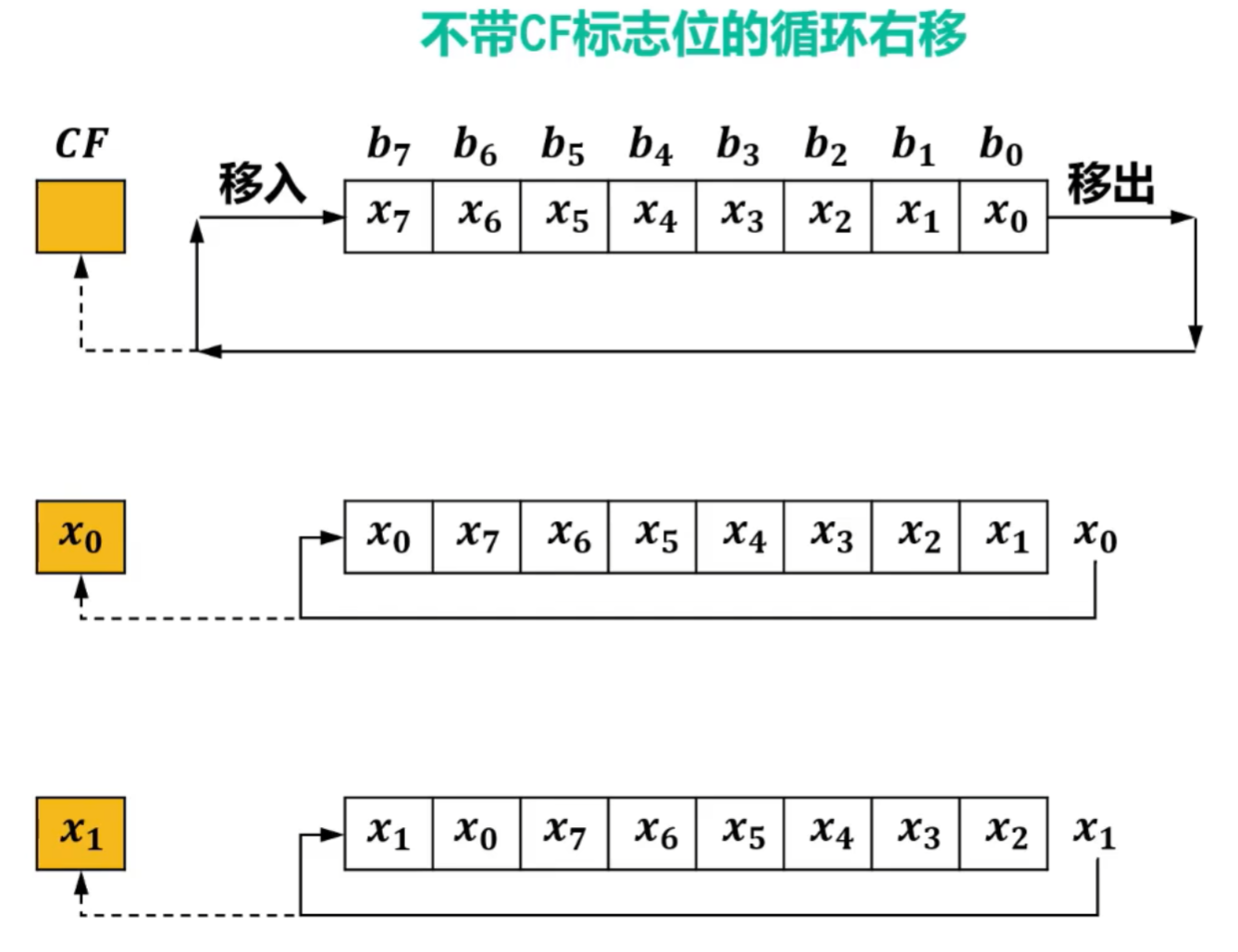
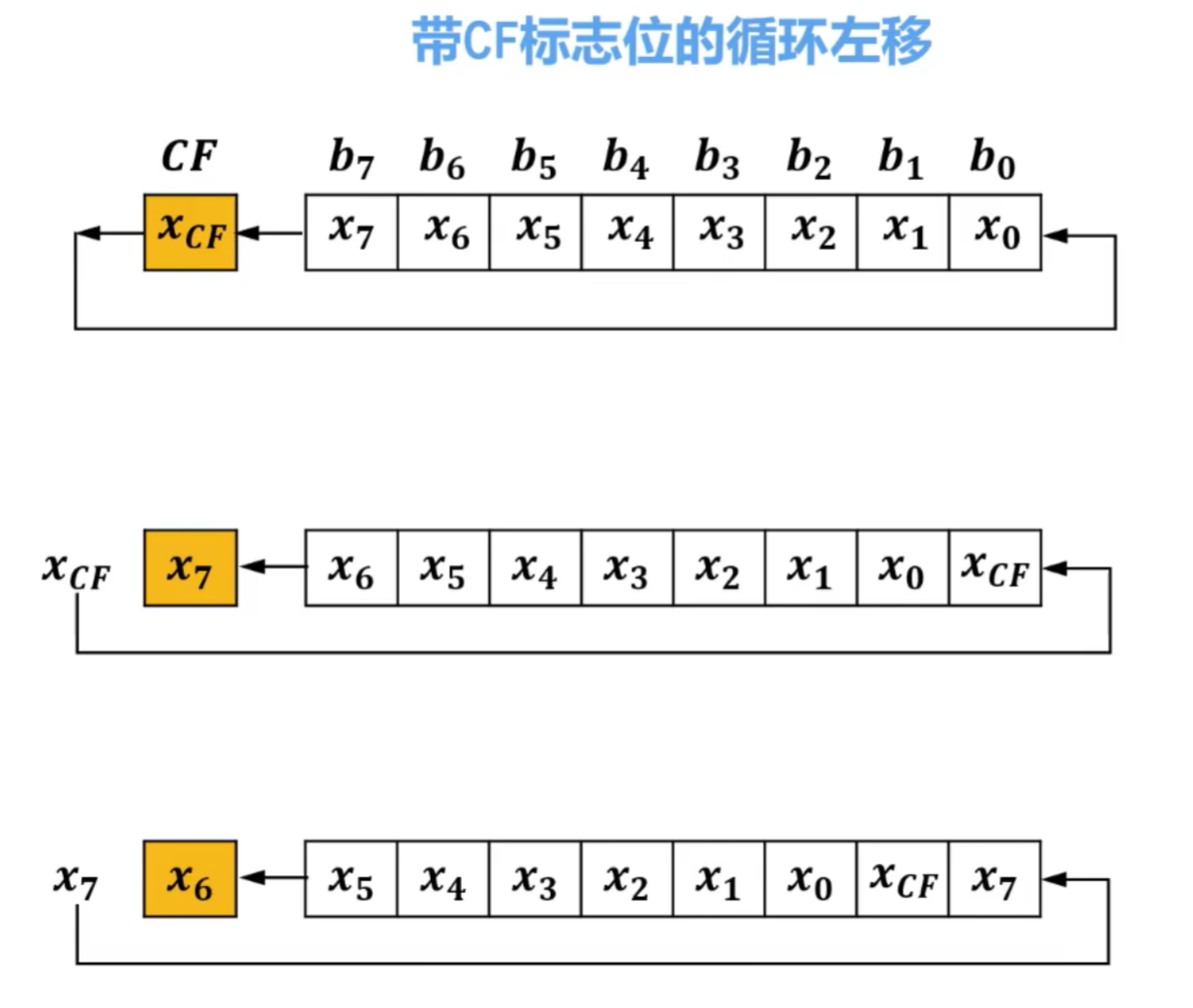
- 循环移位的对象:无符号数
- 将无符号数二进制形式中的各个位向左或向右移动,被移出的位会重新出现在另一端,形成循环。
- 在很多处理器架构中,循环移位指令会影响状态寄存器中的进位标志CF(Carry Flag)位,CF标志位用于标识在执行算术或逻辑操作时是否发生了进位。
- 根据CF标志位是否加入循环移位过程,循环移位可分为以下四种:
- 小循环
- 不带CF标志位的循环右移
- 不带CF标志位的循环左移
- 大循环
- 带CF标志位的循环右移
- 带CF标志位的循环左移
- 小循环
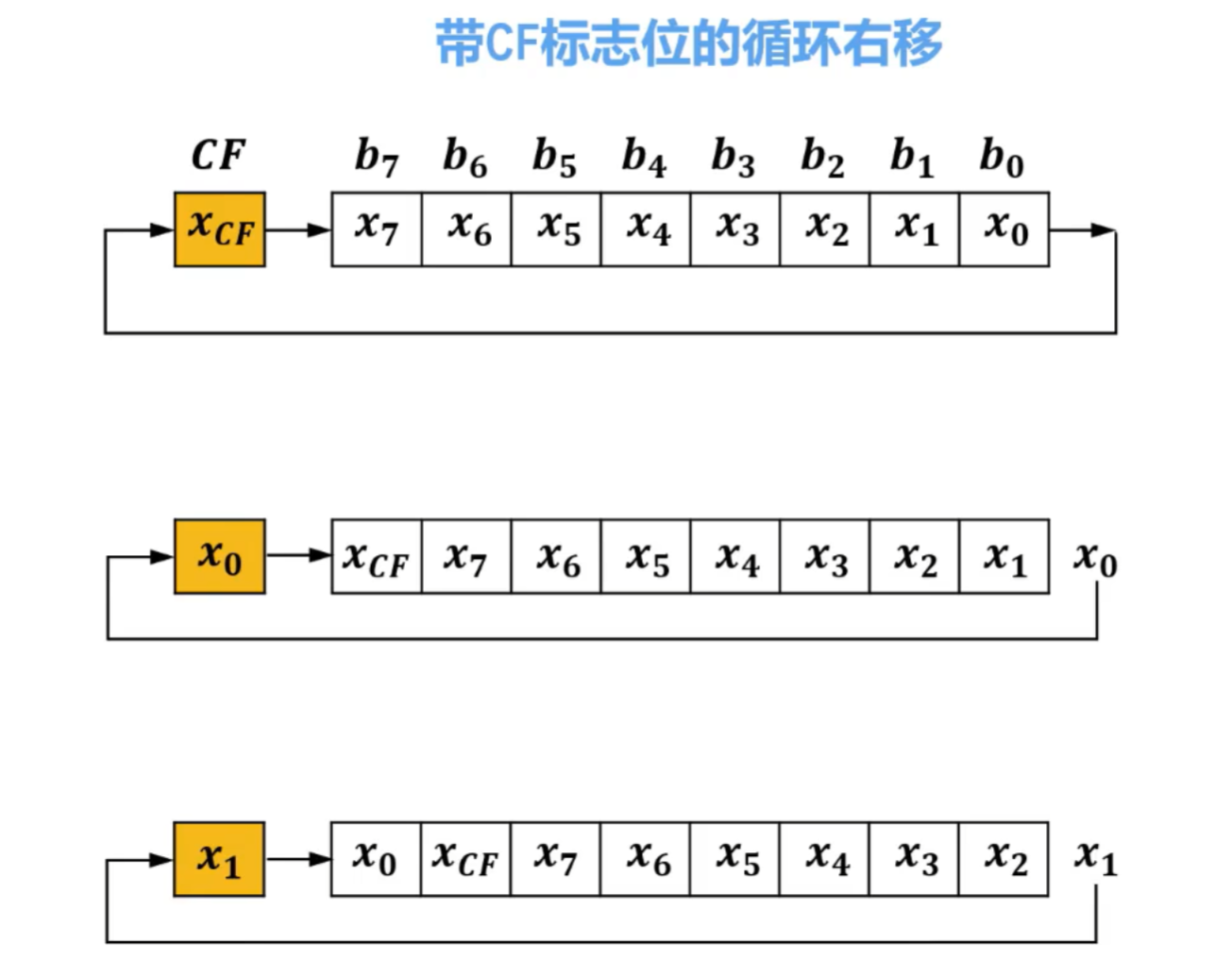
①CF标志位
图例所示:
不带CF标志位的循环左移
不带CF标志位的循环右移
带CF标志位的循环左移
带CF标志位的循环右移
②循环移位的应用
循环移位的应用主要有:加密算法、哈希函数、优化算法
- 加密算法:通过循环移位可以实现数据的混淆和置换,增强加密算法的安全性。
- 哈希函数:通过循环移位可以用来改变辑入数据的排列顺序,以产生不同的哈希值,有利于增强哈希函数的混淆性和扩散性。
- 优化算法:在某些算法中,循环移位可以,用于优化性能和节省资源。例如,在图形处理和数字信号处理中,循环移位可以月于加速算法的执行。
③循环移位的C语言实现
C语言中并没有直接提供循环移位操作符
- 通常情况下,可以使用移位运算操作符(例如:左移“ << ”或右移“ >> ”)和位运算操作符(例如:或运算 “ | ”)来实现。
C语言实现:
#include <stdio.h>
/* 循环左移 */
unsigned int circularLeftShift(unsigned int value, int n) {
return (value << n) | (value >> (32 - n));
}
/* 循环右移 */
unsigned int circularRightShift(unsigned int value, int n) {
return (value >> n) | (value << (32 - n));
}
int main() {
unsigned int usi = 0x12345678; // 待循环移位的32位无符号整数
int d = 4; // 移位距离(即一次循环移动几位)
printf("Original value: 0x%x\n", usi);
printf("Circular left shift by %d bits: 0x%x\n", d, circularLeftShift(usi, d));
printf("Circular right shift by %d bits: 0x%x\n", d, circularRightShift(usi, d));
return 0;
}
2、定点数的加减法运算
1)补码加减法运算公式

例题:
加法
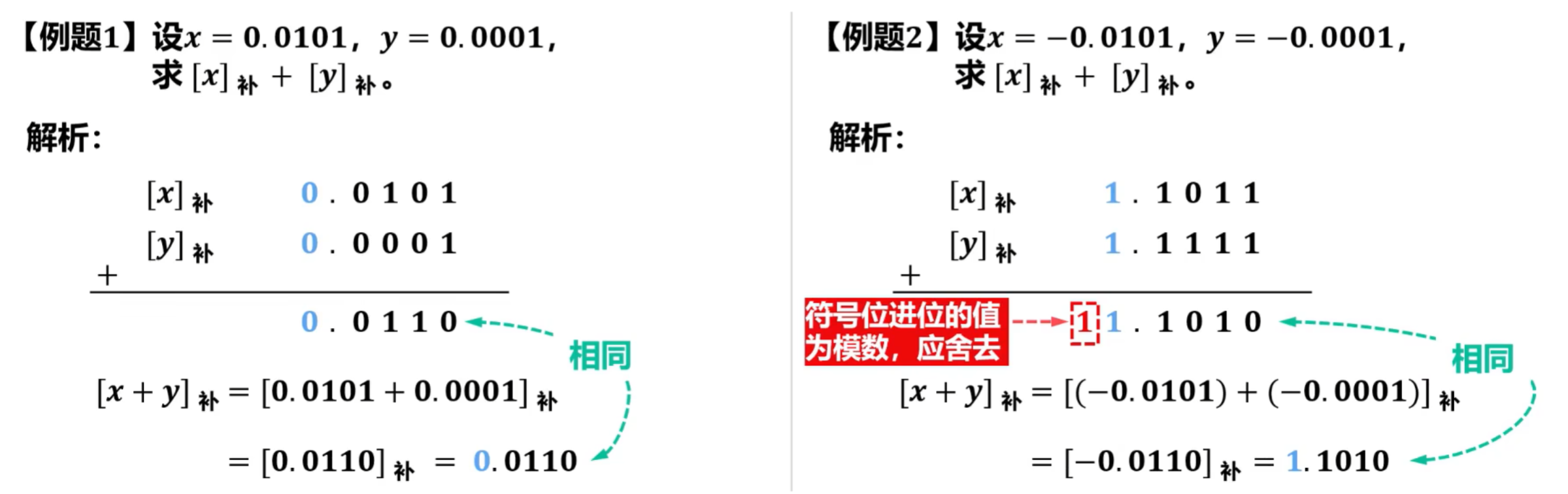

减法



2)补码加减法运算的溢出检测
①溢出的概念
- 计算机的字长是有限的,因此所能表示的数据范围也是有限的。
- 当运算结果超出所能表示的数据范围时,就会出现溢出(Overflow)
- 溢出会导致错误的运算结果;
- 计算机系统设计人员必须要解决溢出的检测问题,以便在发生溢出时计算机能做出相应的处理。

②检测溢出
-
定点数补码加减运算判断溢出的方法主要有以下3种:
-
根据操作数的符号位与运算结果的符号位是否一致进行判断;


逻辑表达式:下图中,x,y,z的上划线表示取反

-
根据运算过程中最高数值位的进位与符号位的进位是否一致进行判断;


逻辑表达式:

-
利用变形补码(具有2位符号位的补码)的符号位进行判断。


逻辑表达式:⊕表示为异或

例题:
题1、法一

法二

题2、

题3、法一

法二

16位定点补码所能表示定点整数的取值范围:-216-1 ≤ x ≤ 216-1的取值范围是[-32768,327677]
题4、

-
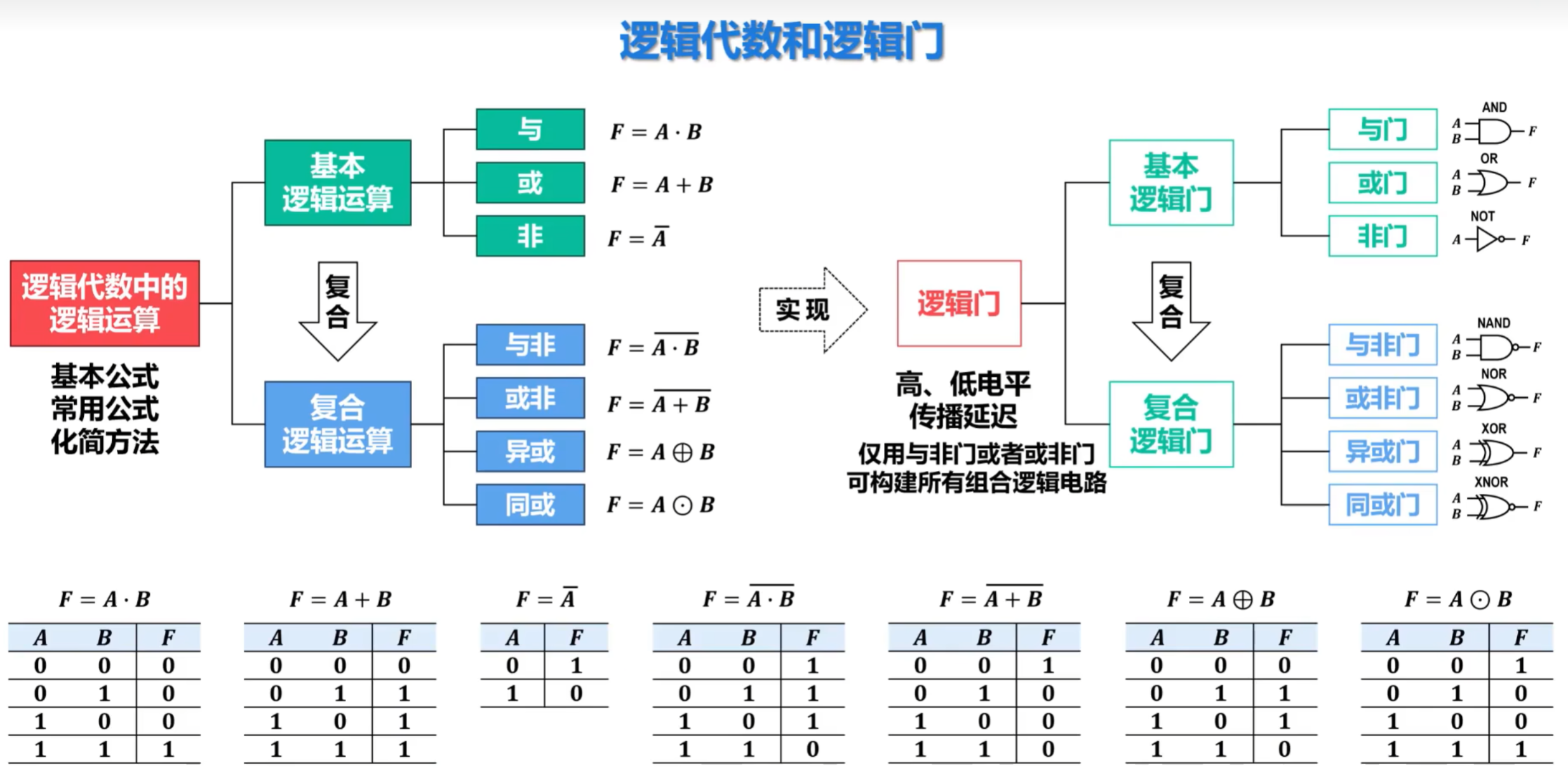
3)逻辑代数和逻辑门
①基本梗概
- 逻辑代数的逻辑运算
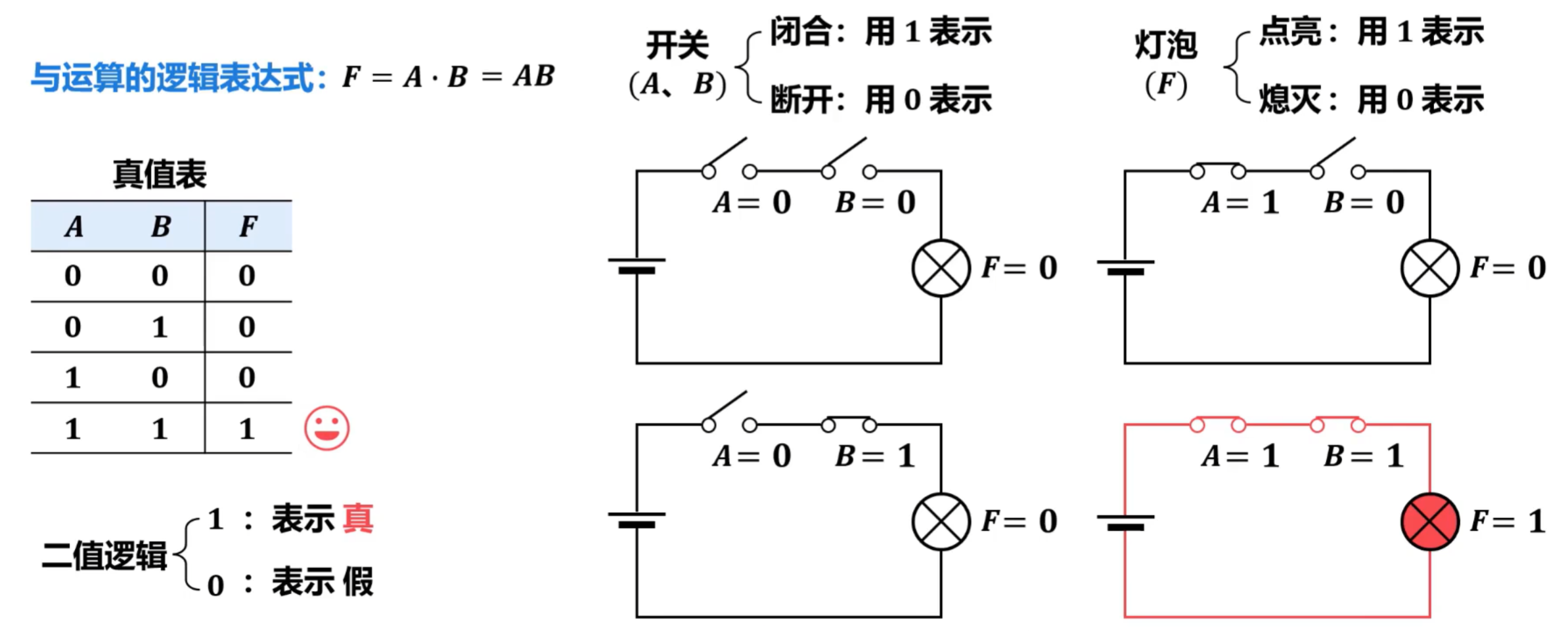
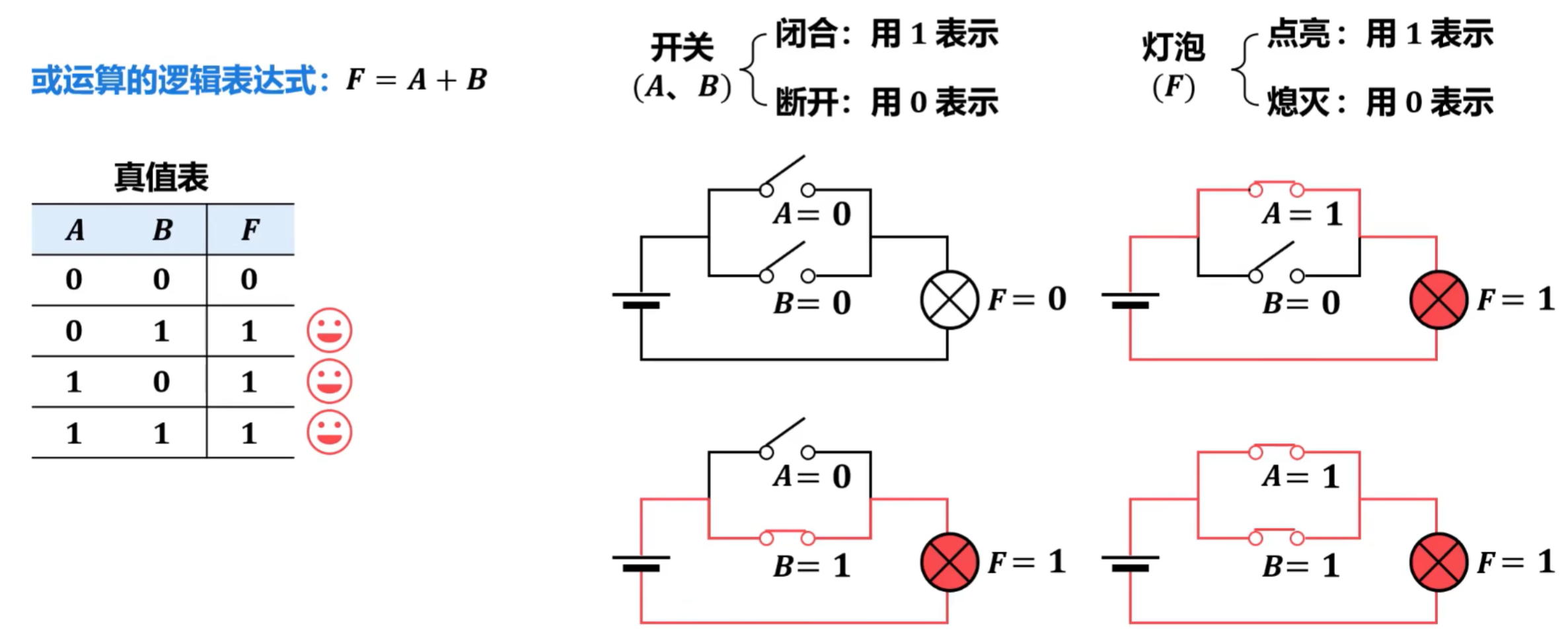
- 基本逻辑运算
- 与、或、非
- 复合逻辑运算(由基本逻辑运算复合得到)
- 与非、或非、异或、同或
- 基本逻辑运算
- 逻辑门(实现逻辑运算的电路)
- 基本逻辑门
- 与门、或门、非门
- 复合逻辑门(由基本逻辑门复合得到)
- 与非门、或非门、异或门、同或门
- 基本逻辑门
②基本逻辑和逻辑门运算
- 与运算和与门

- 或运算 和 或门
- 非运算 和 非门
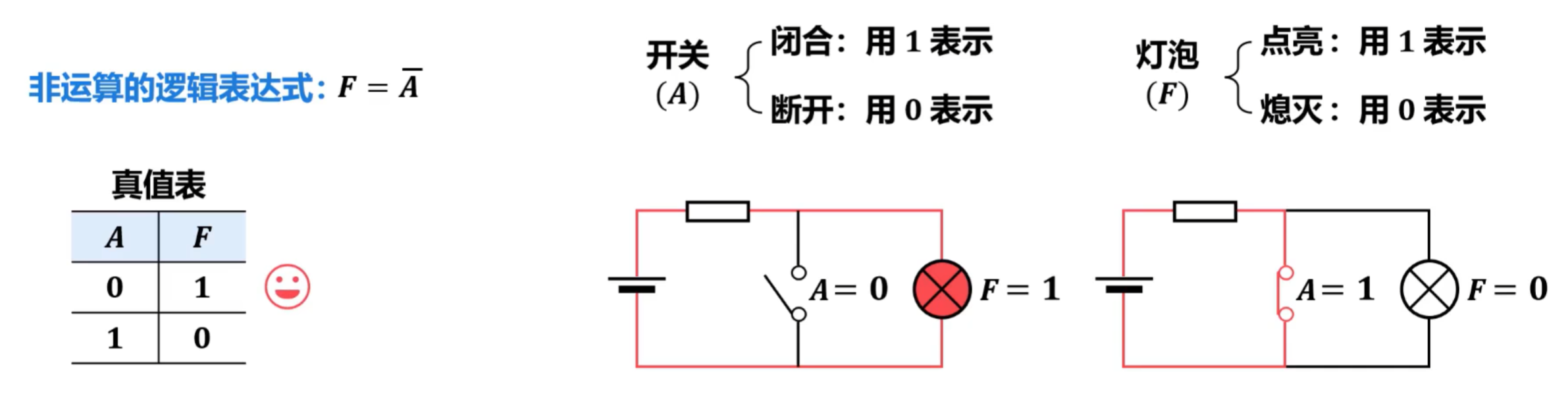

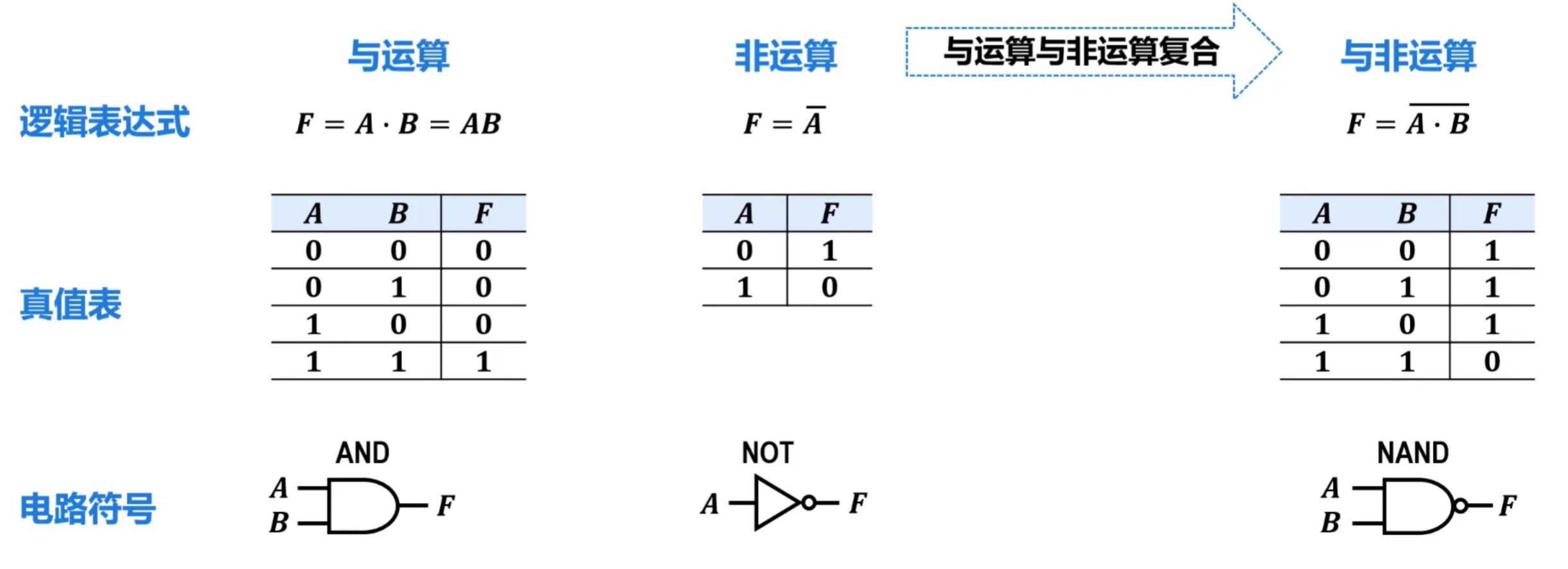
③复合逻辑和复合逻辑门运算
- 与非运算 和 与非门
反演律

重叠律

还原律
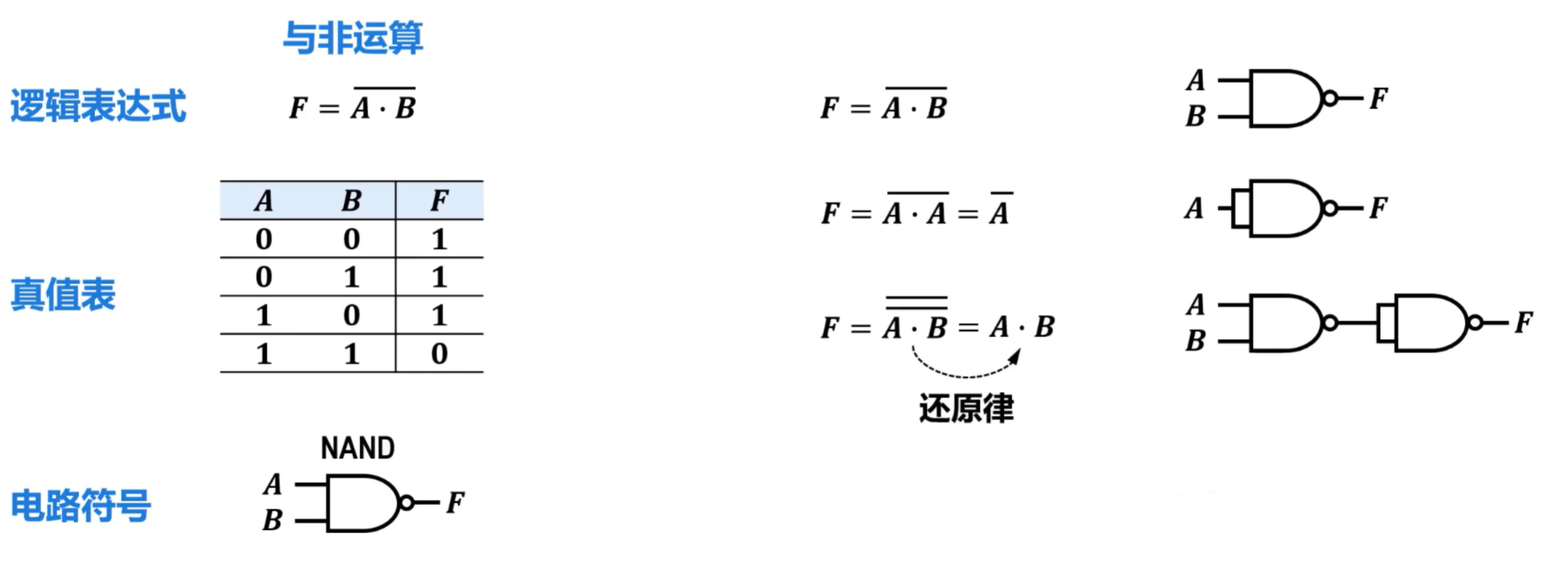
仅使用与非门可以构建所有组合逻辑电路

- 或非运算 和 或非门
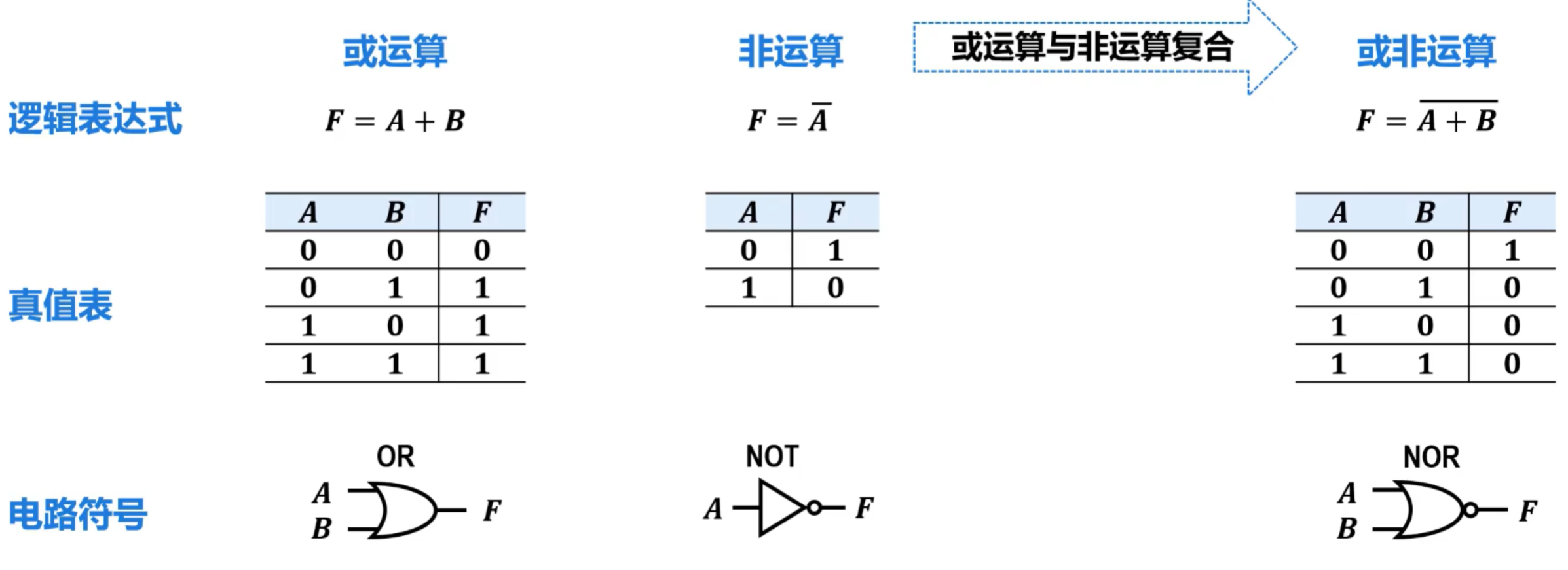
同与非门一样,仅使用或非门也可以构建非门、或门、与门,甚至可以构建任何组合逻辑电路。
- 异或运算 和 异或门
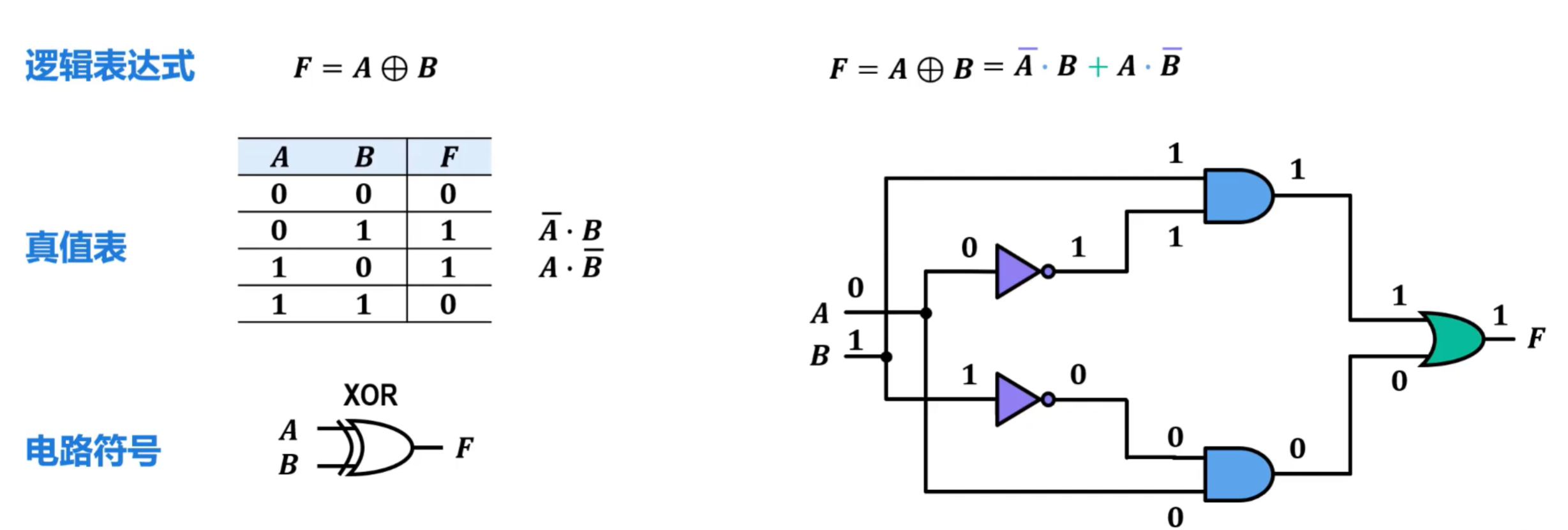
- 同或运算 和 同或门
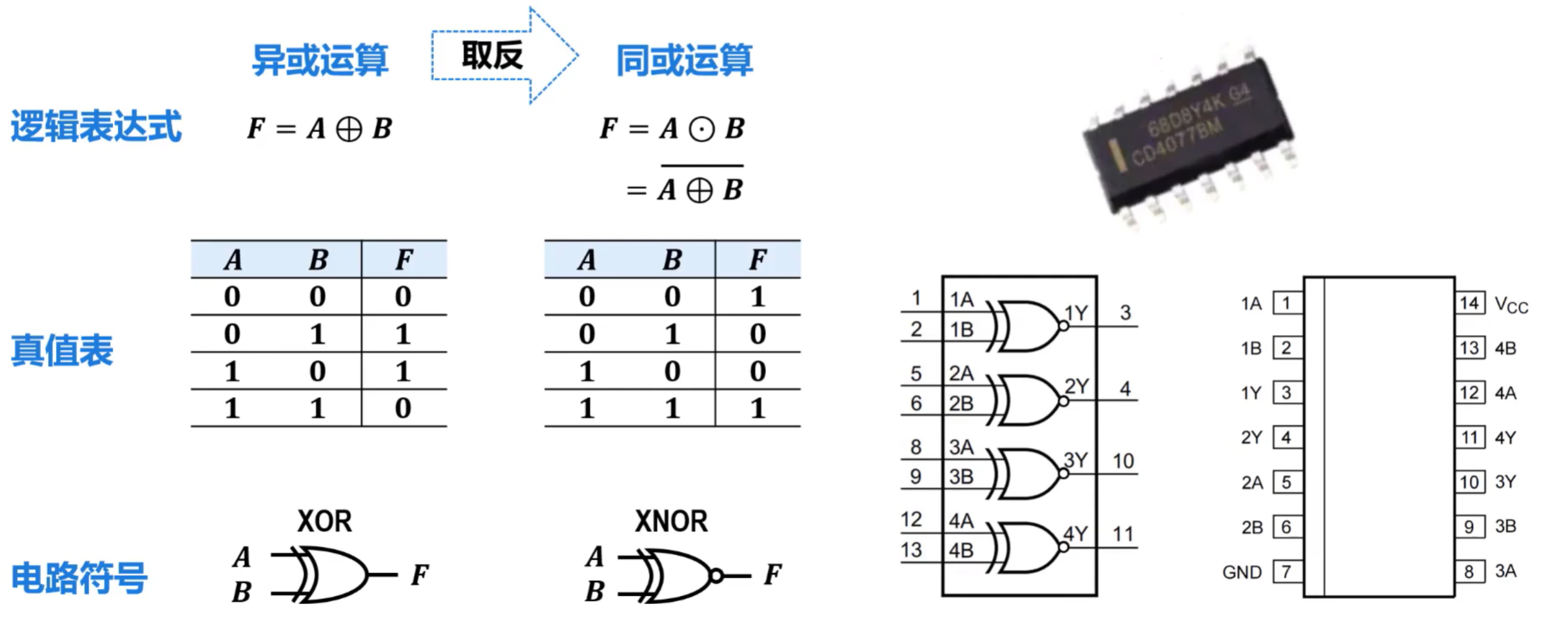
总结:
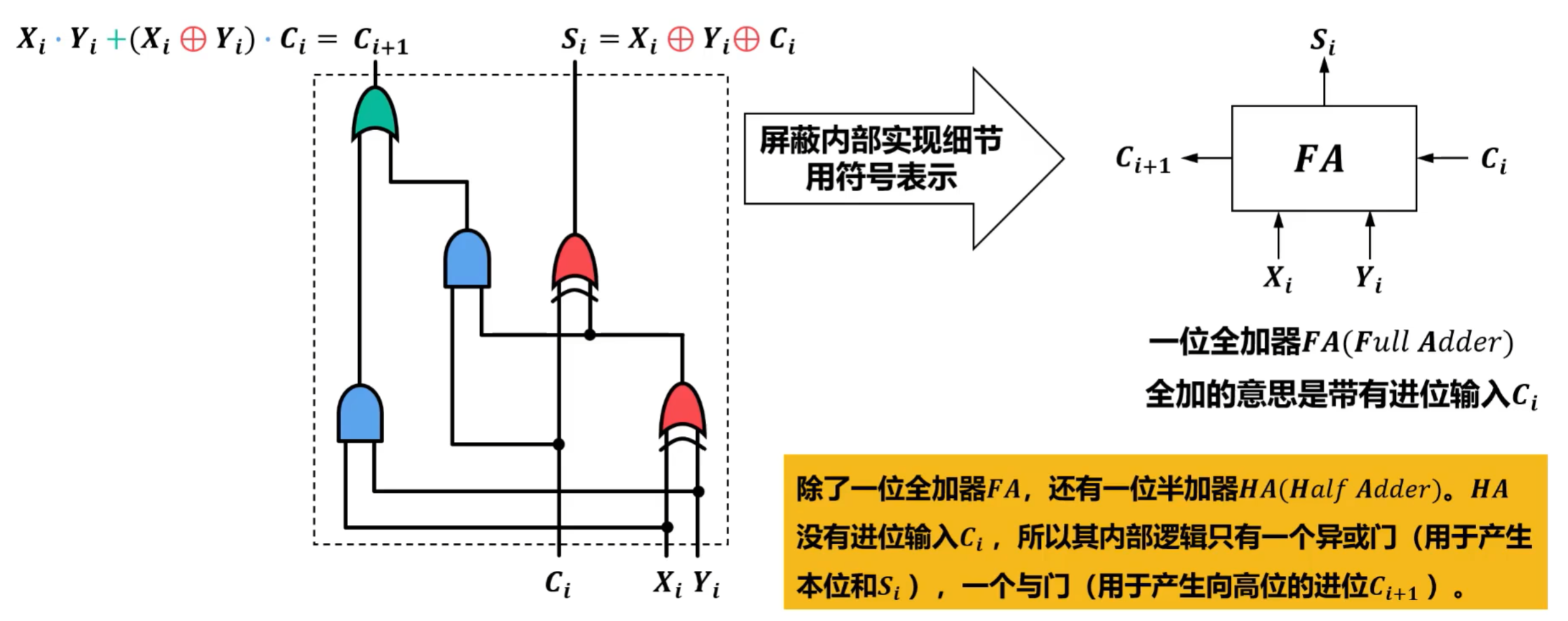
4)一位全加器的硬件逻辑实现
首先记Xi,Yi,Ci,Ci+1,Si
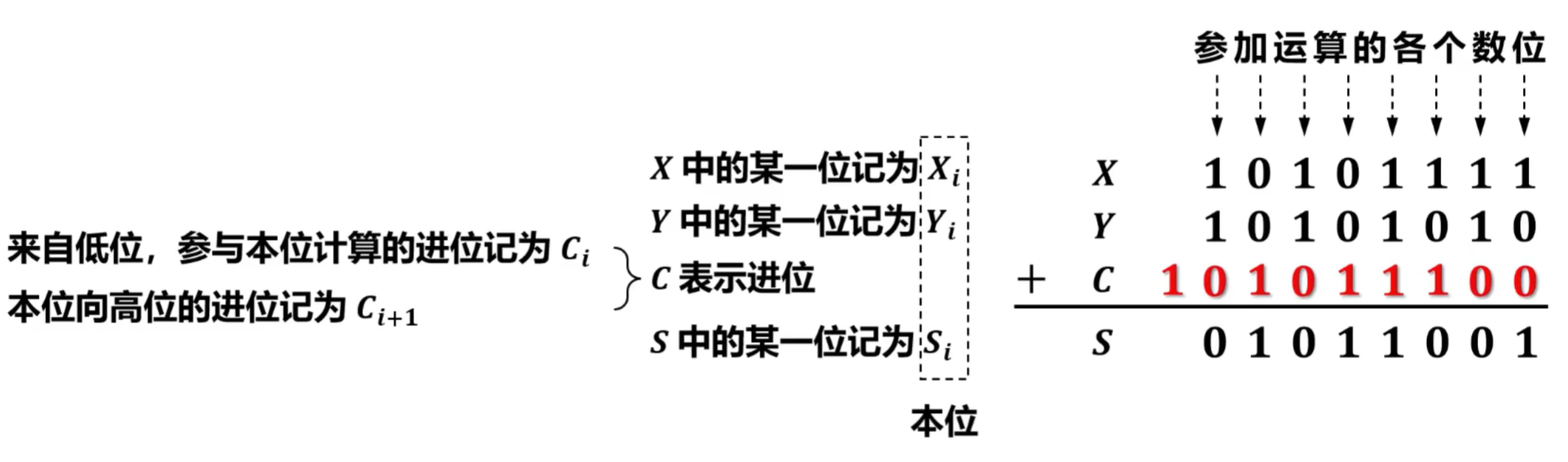
得到真值表
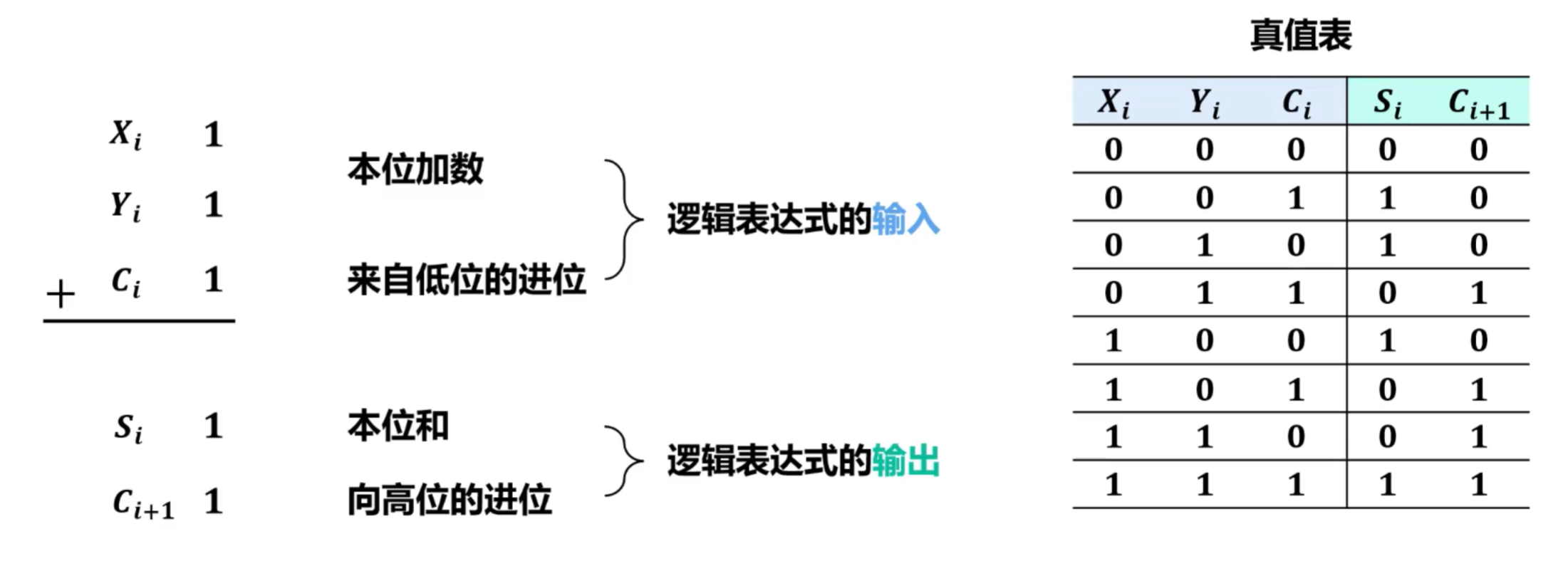
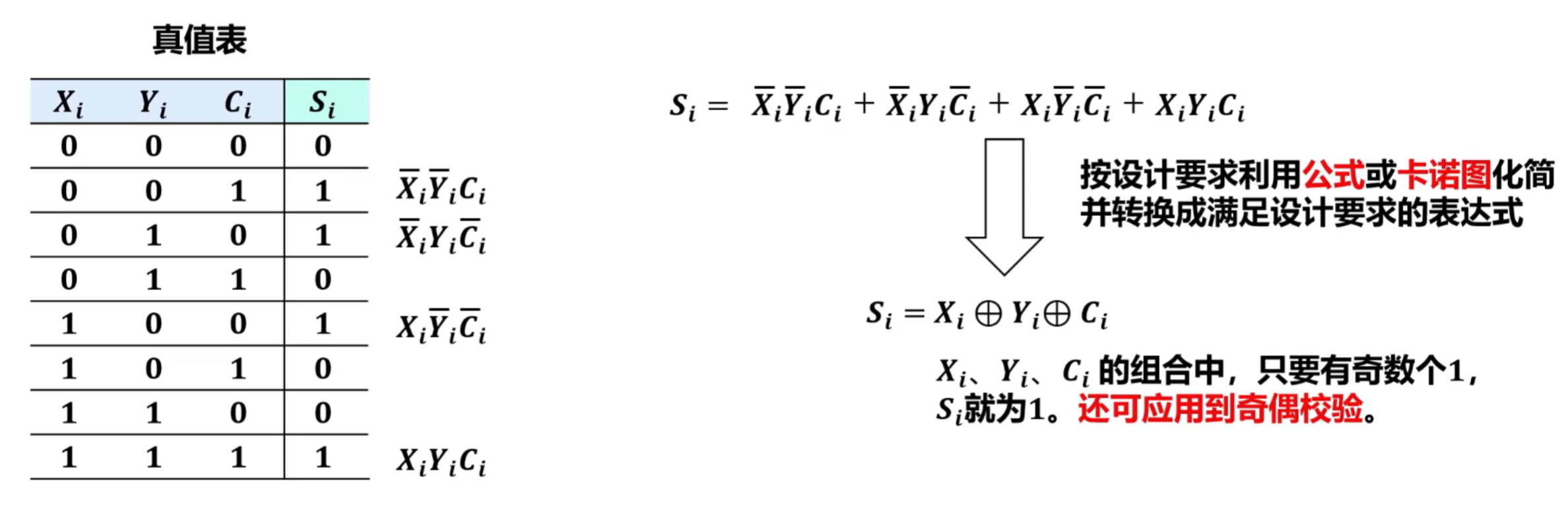
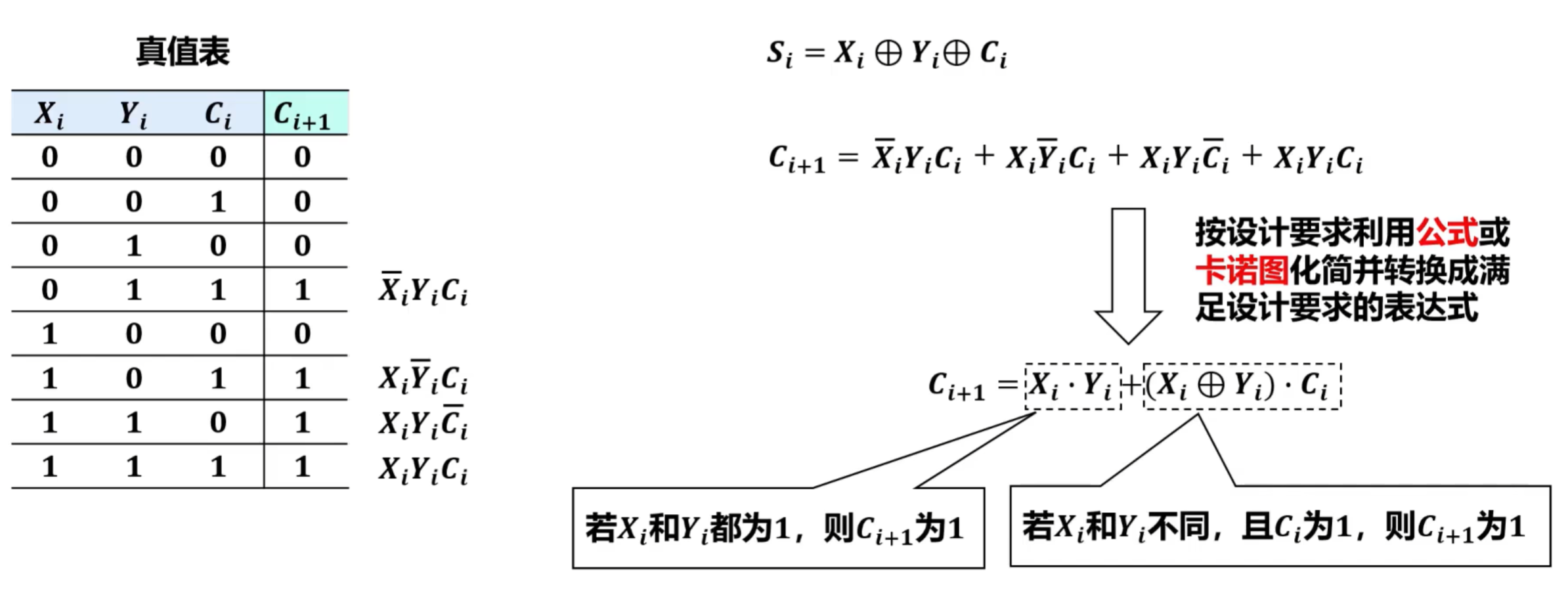
通过真值表得到满足要求的表达式
通过真值表验证逻辑电路图
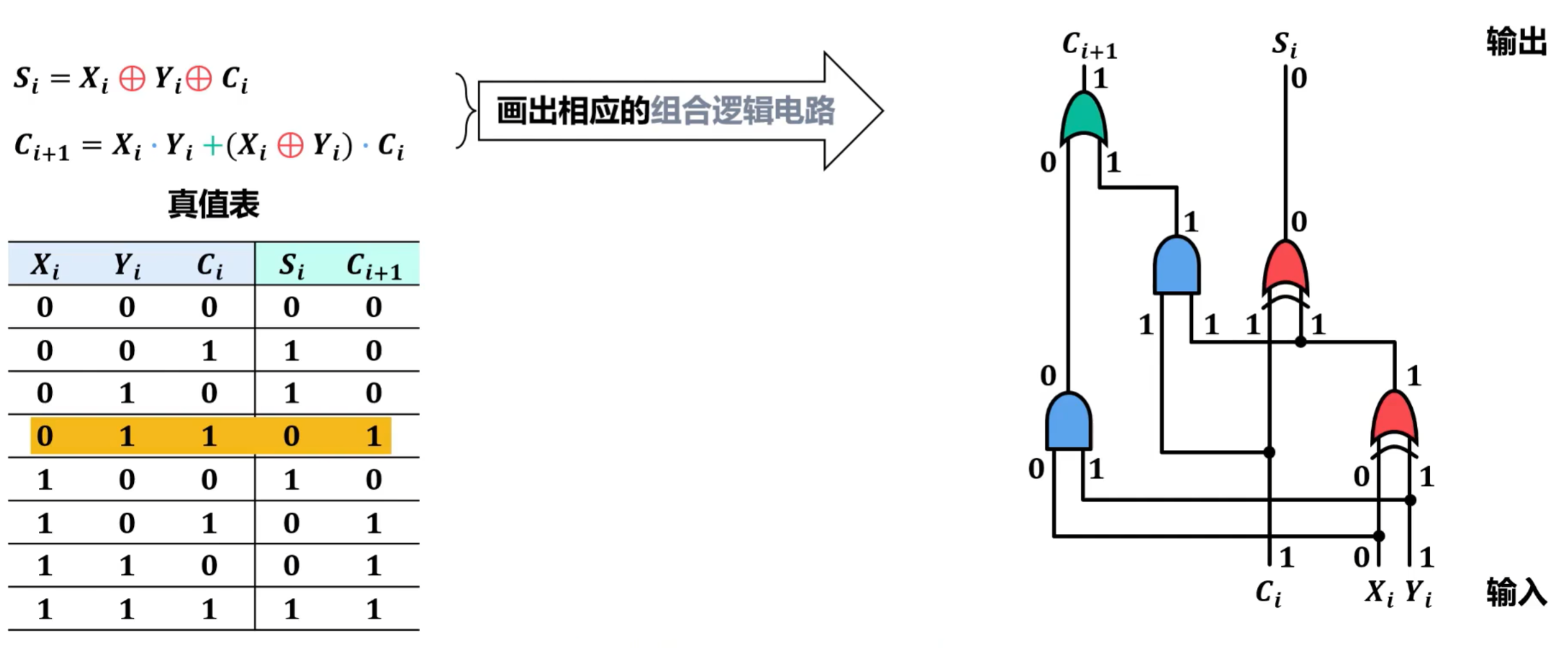
进而,得到了用逻辑门电路实现一位全加器
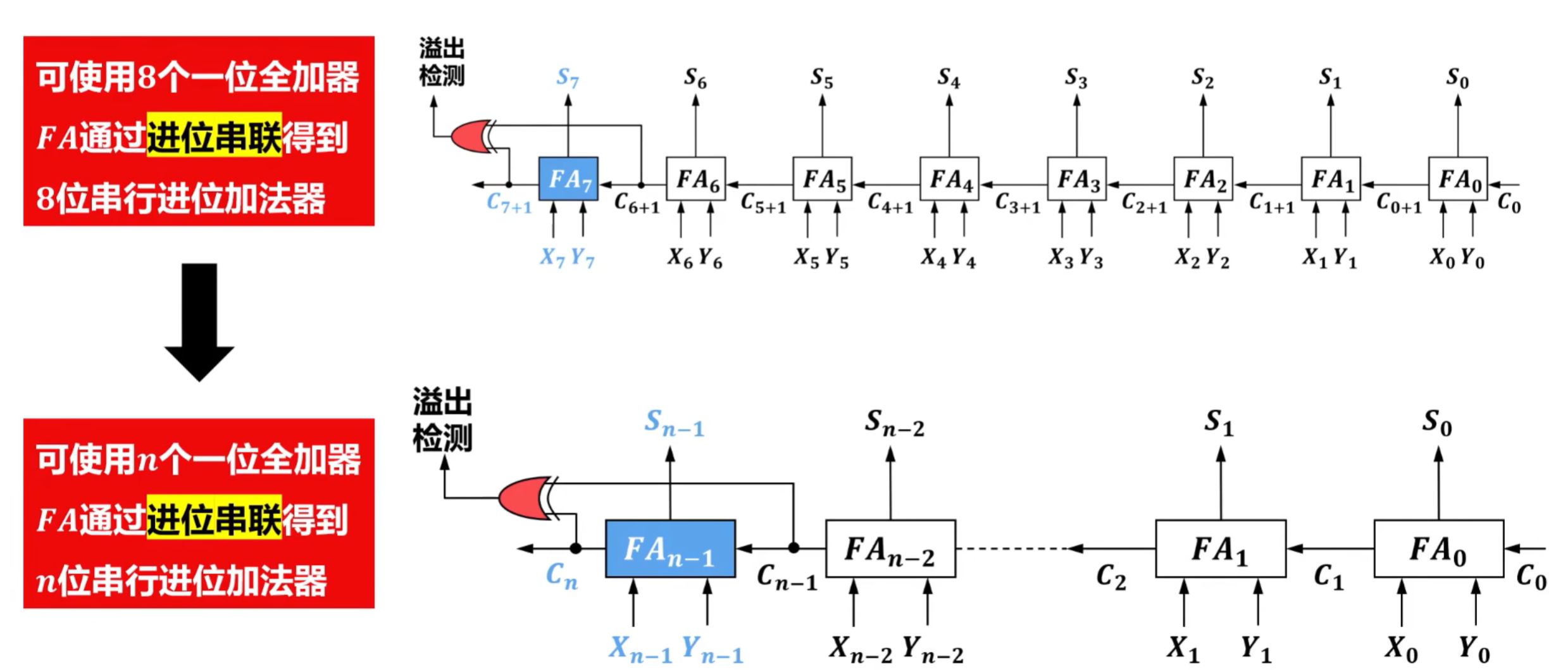
5)串行进位加法器的硬件逻辑实现
使用8个一位全加器FA通过进位串联得到8位串行进位加法器

该电路具备溢出检测功能

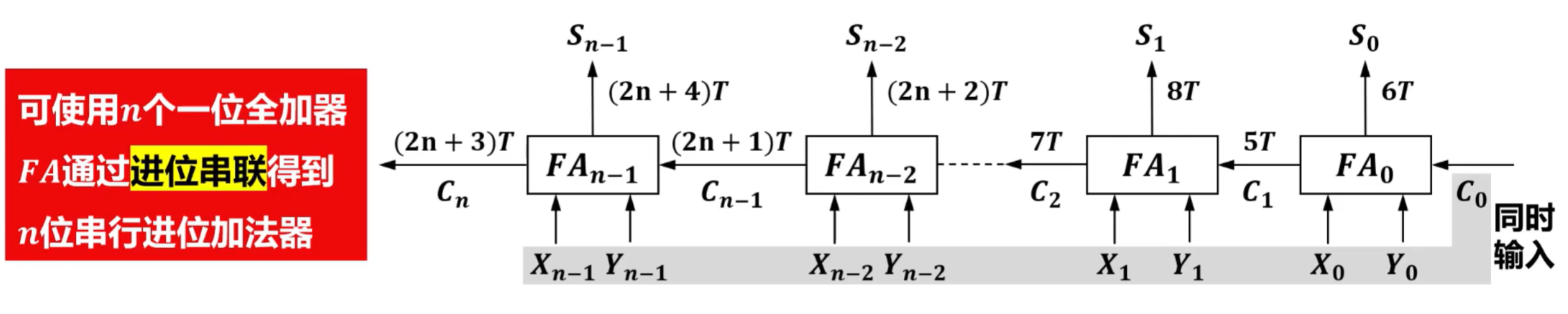
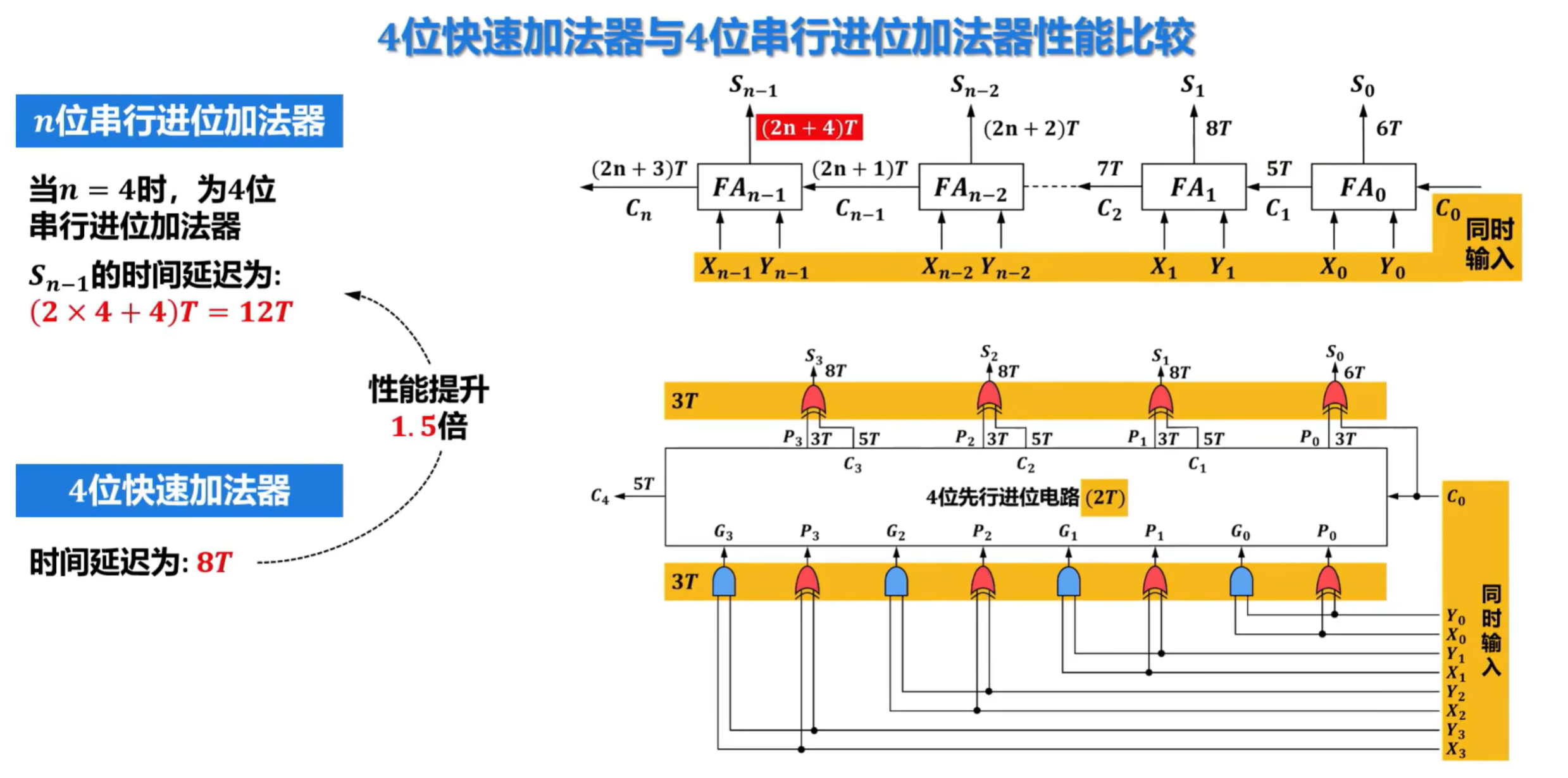
串行进位加法器的性能
- 在n位串行进位加法器中,每个高位的一位全加器FA的运算依赖于相邻低位的一位FA的进位Ci+1,因此所有一位FA不能并行运行,其时间关键延迟为(2n+4)T,与串行进位加法器的位数n呈线性关系,当n较大时性能较差。
例题:
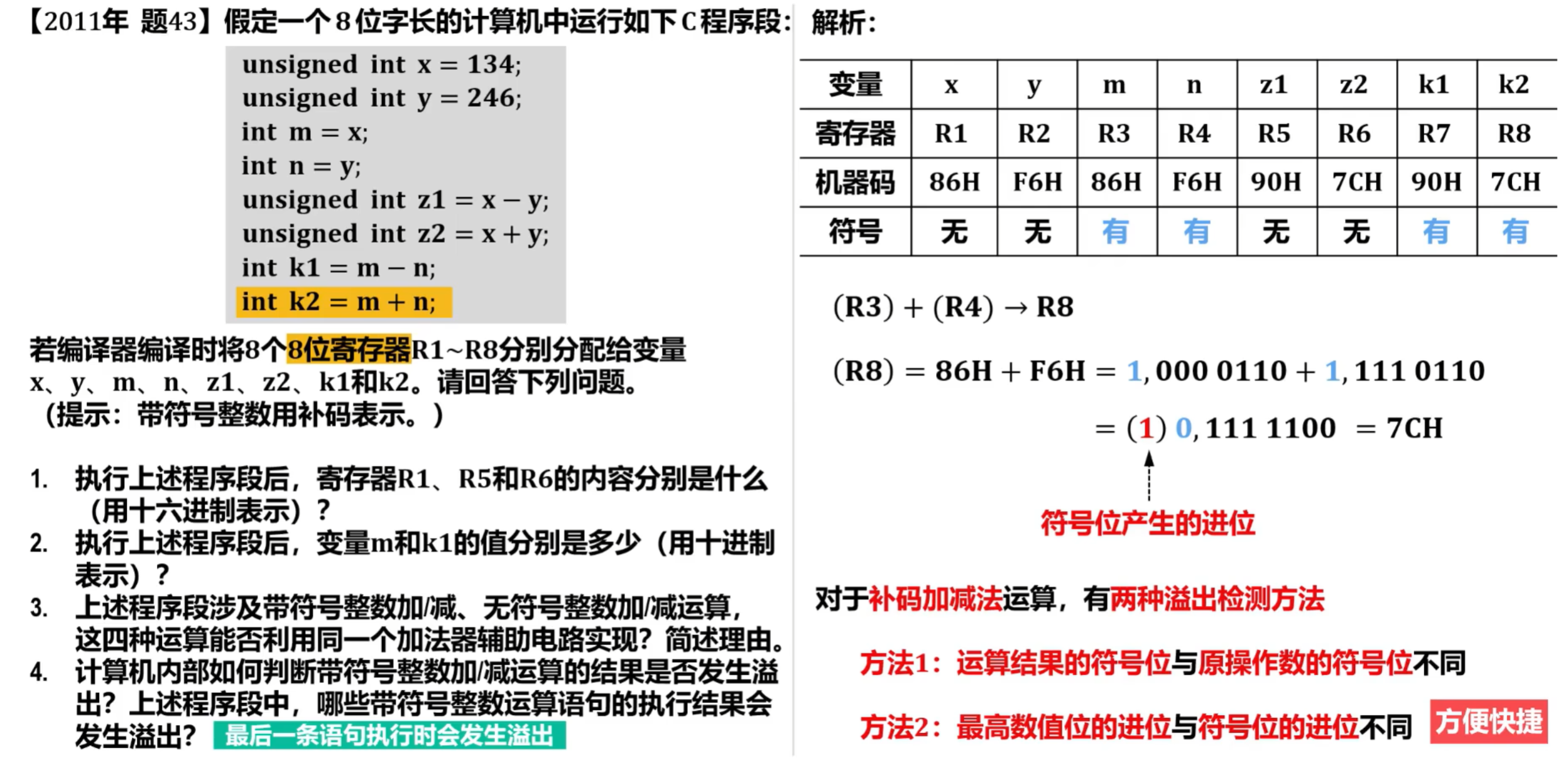
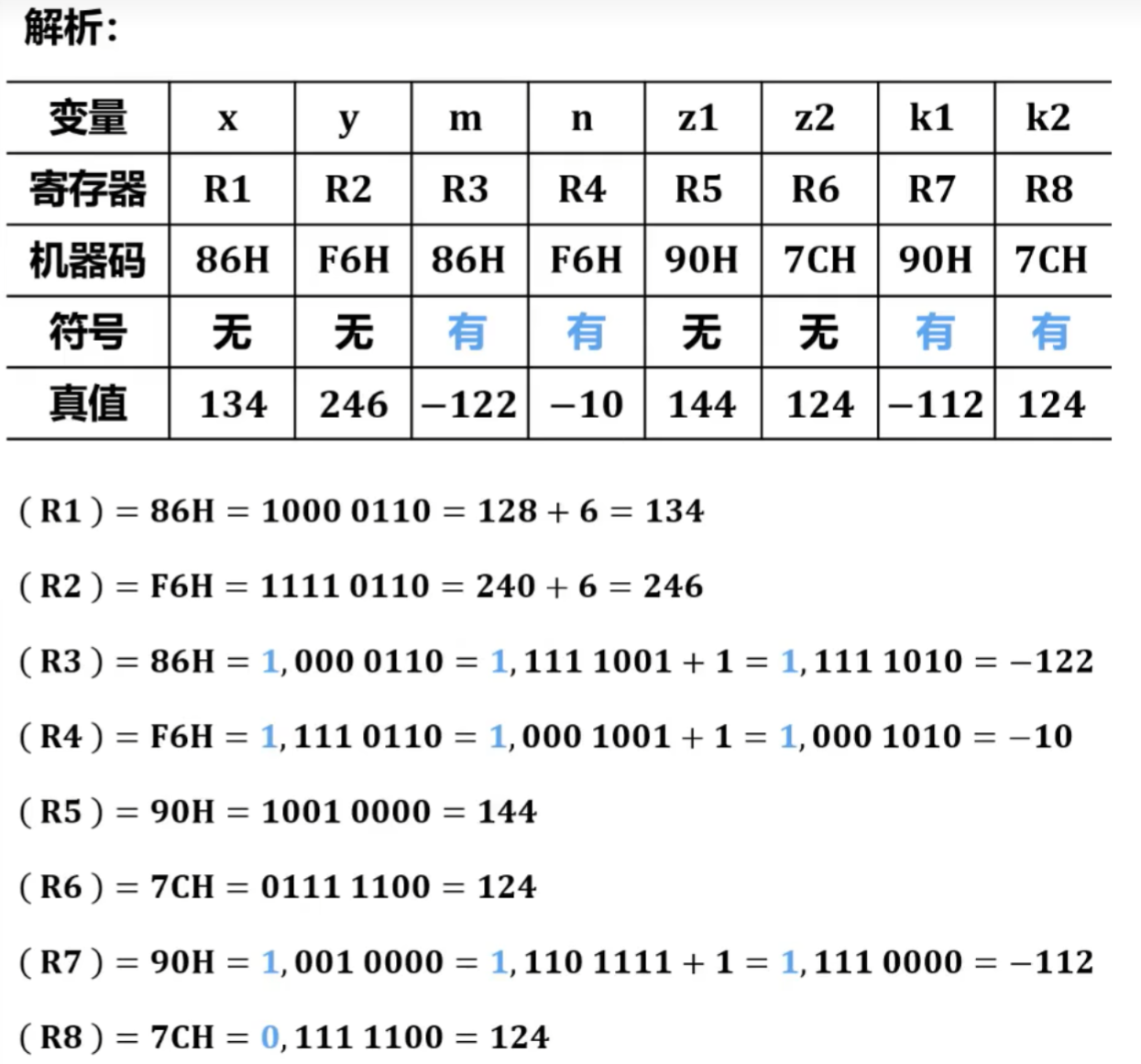
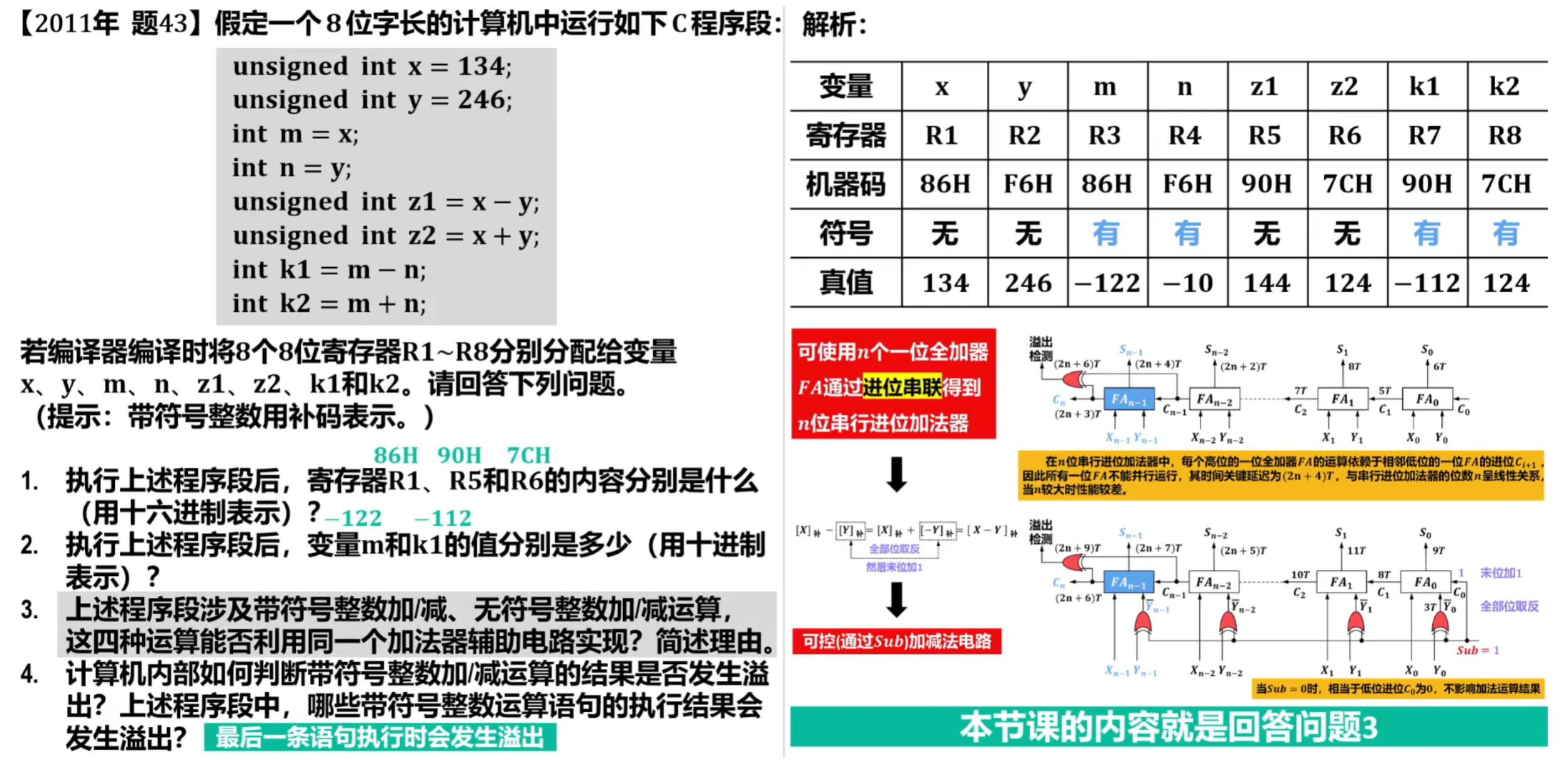
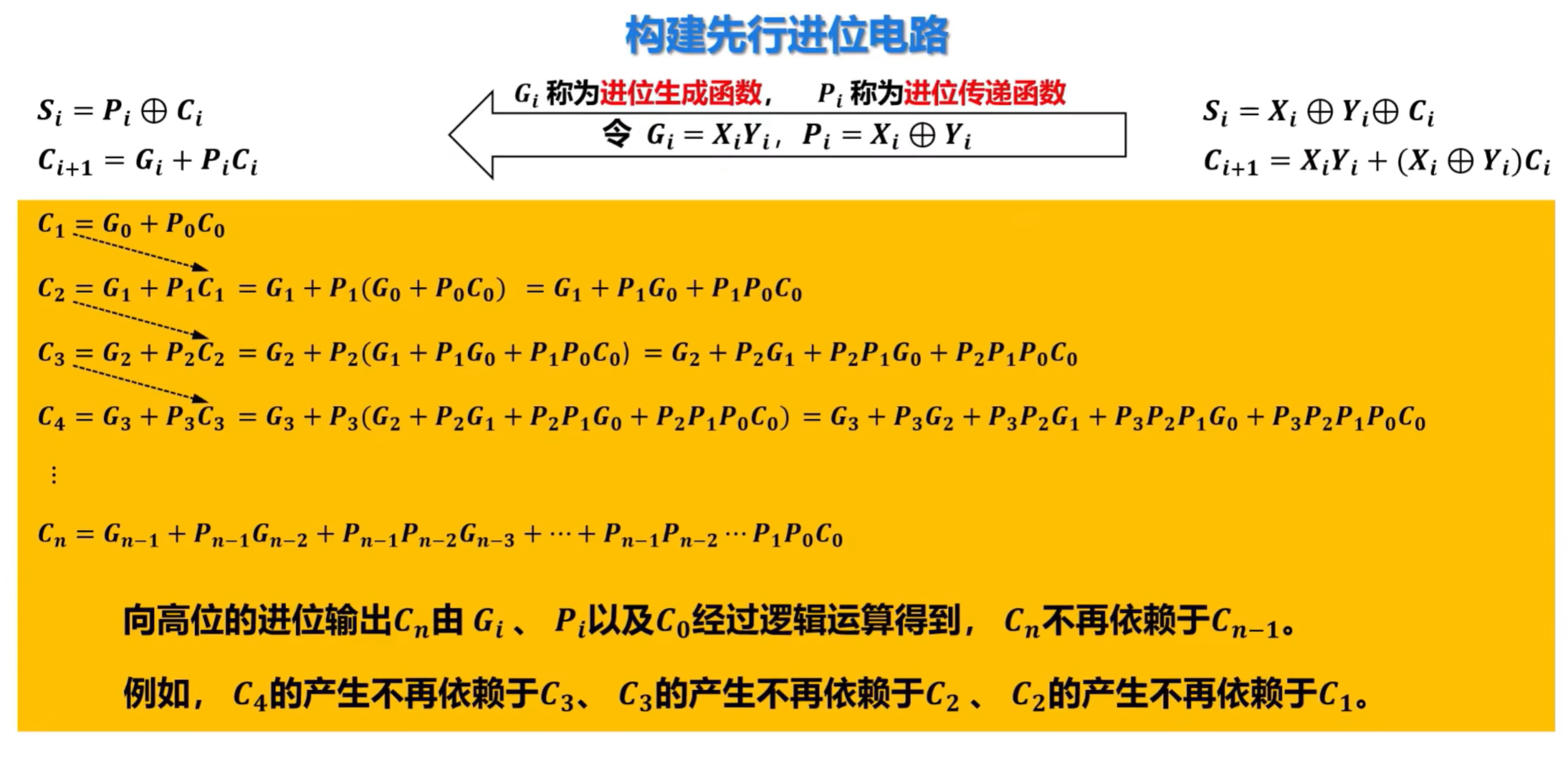
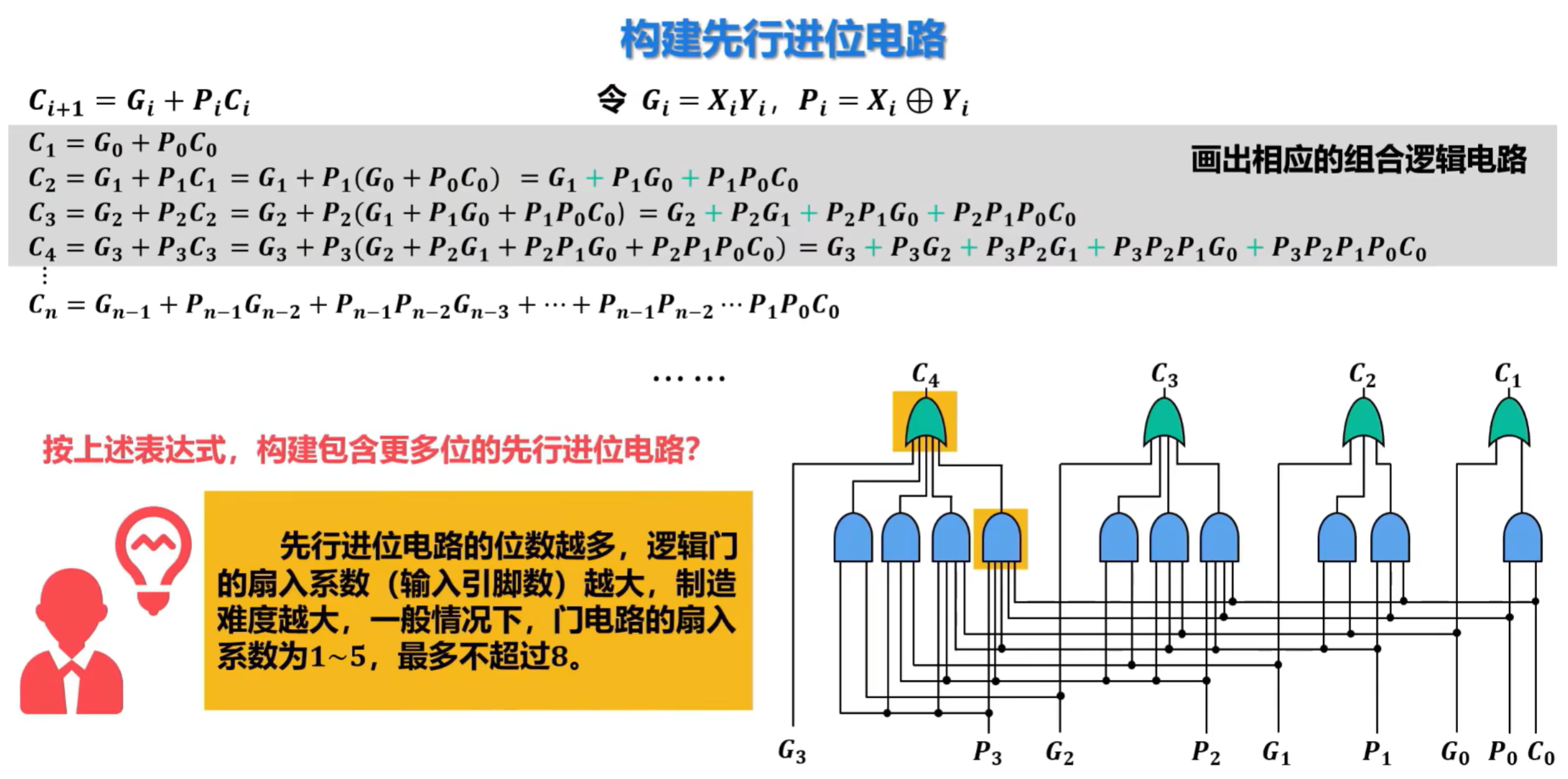
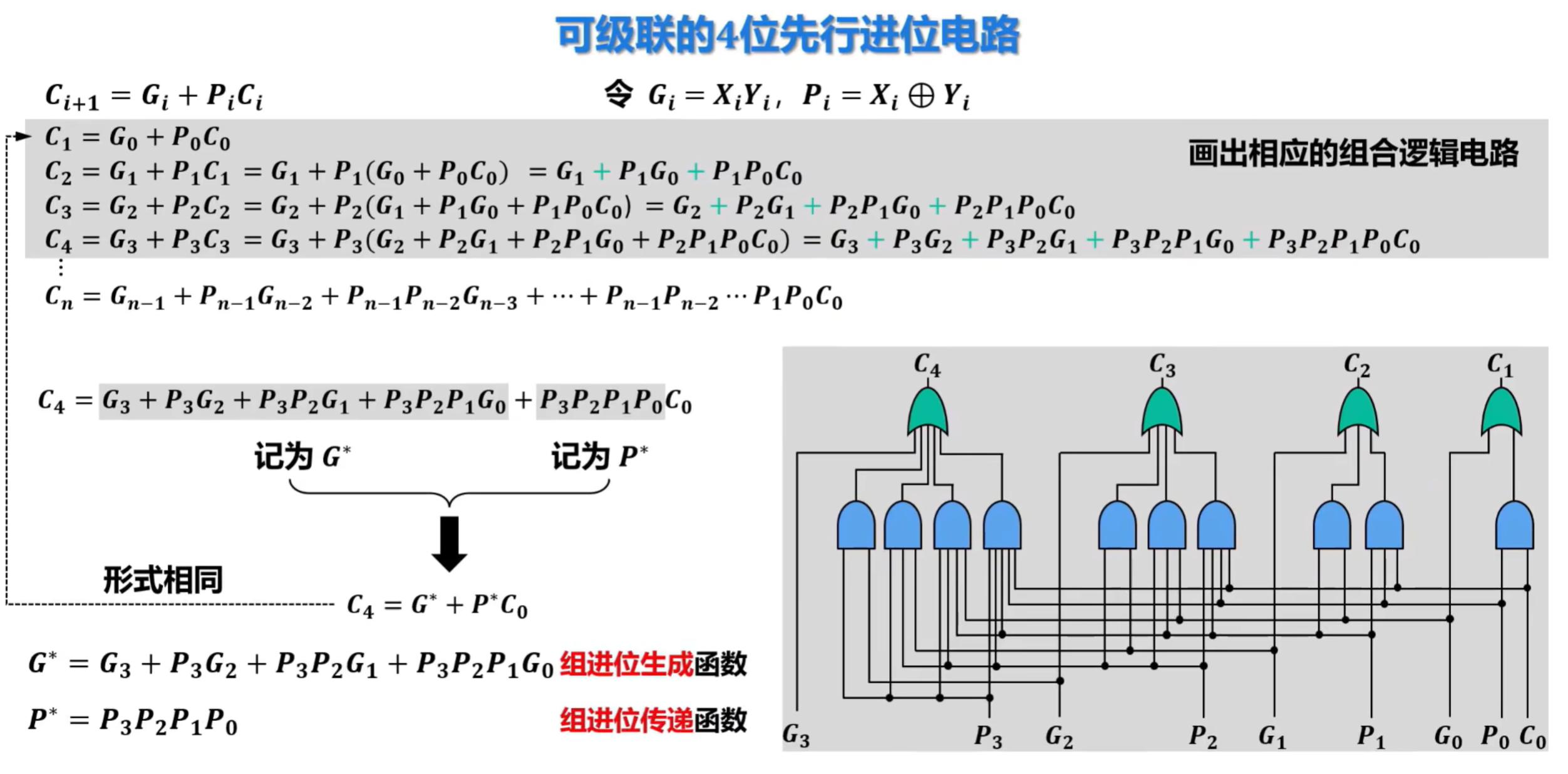
6)先行进位加法器的硬件逻辑实现
难点,建议看视频学习:https://www.bilibili.com/video/BV1qG41197E4?spm_id_from=333.788.player.switch&vd_source=cc2432322b31e1c60d007467270cb1ee&p=30
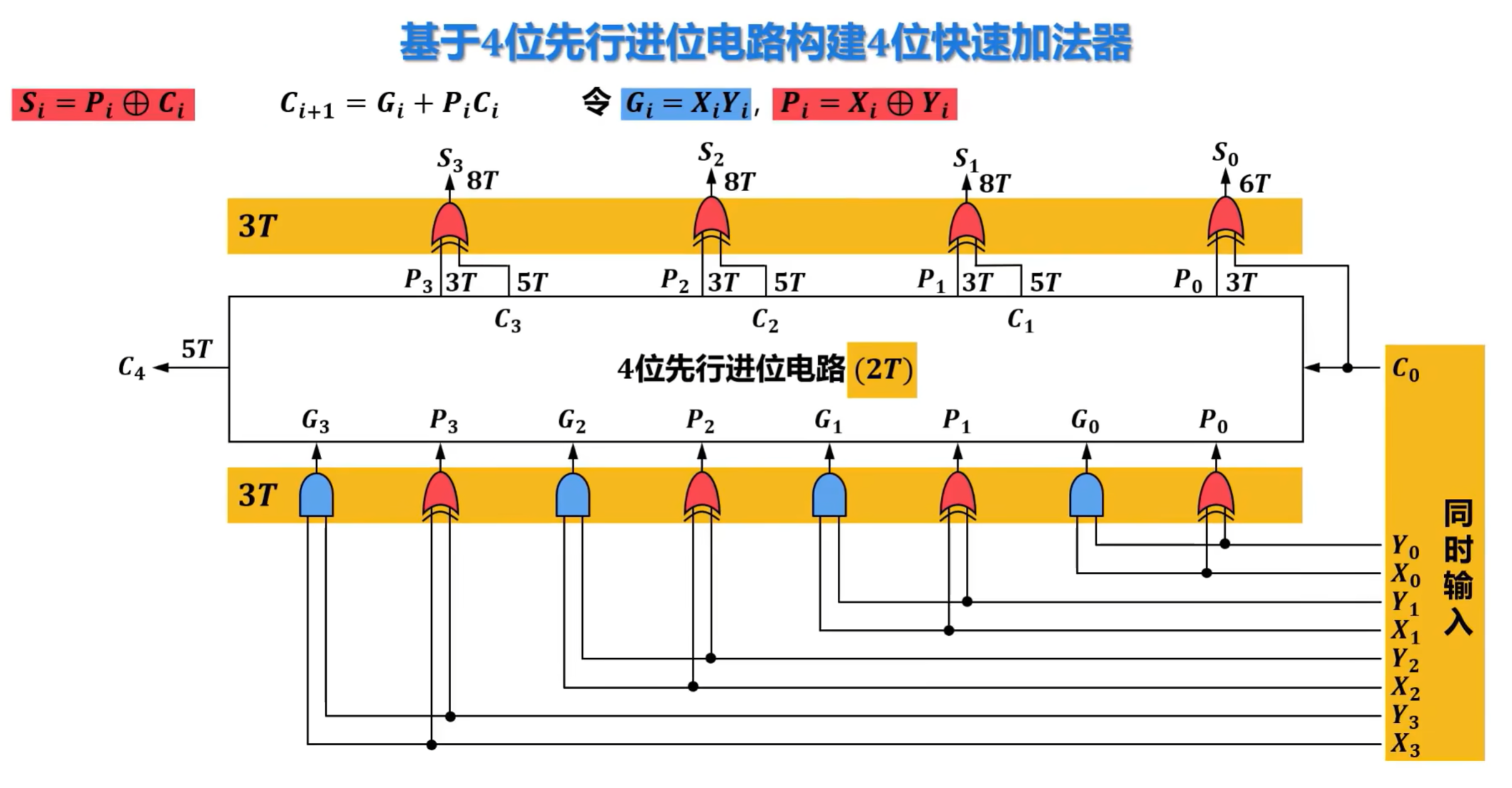
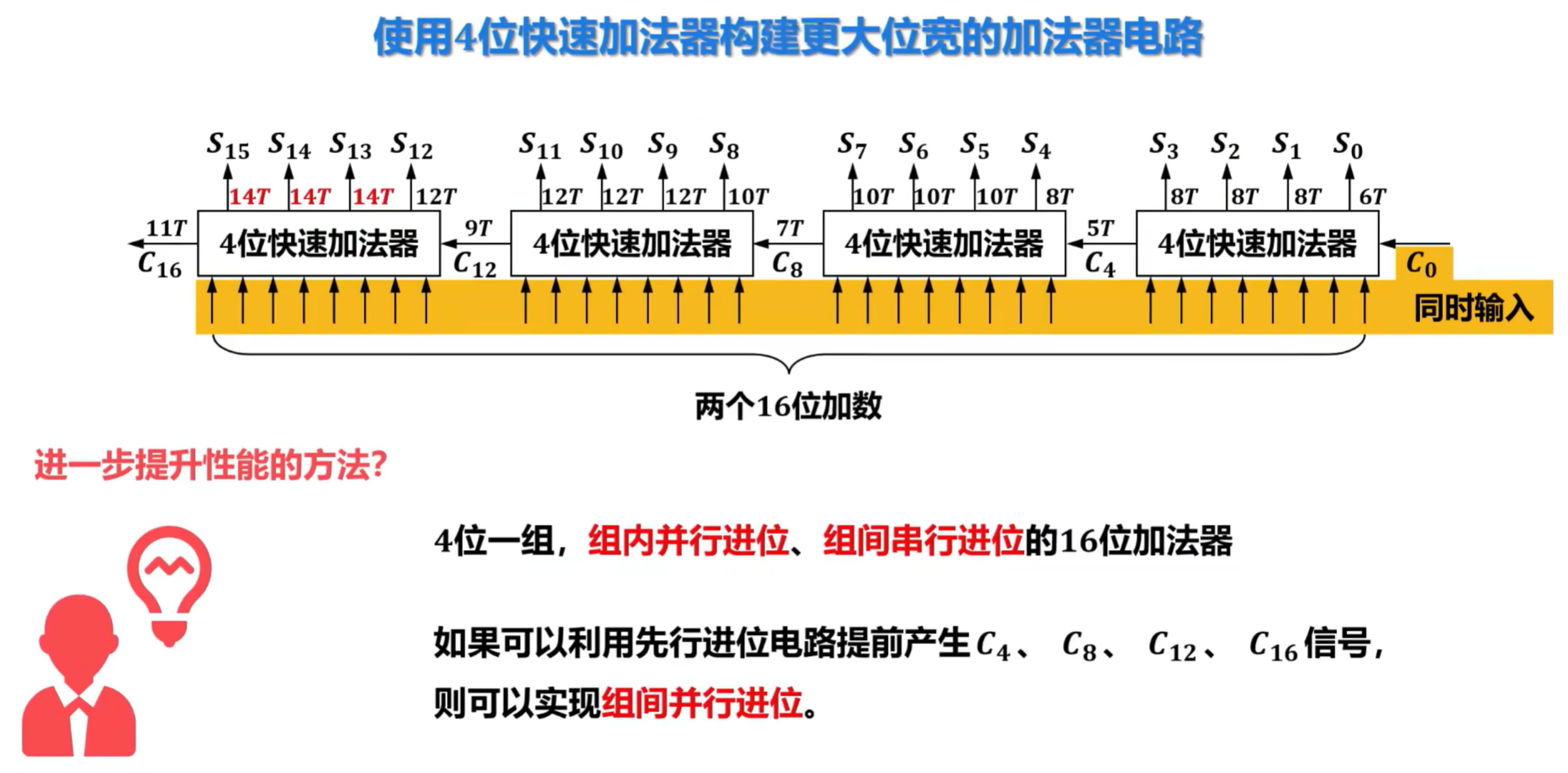
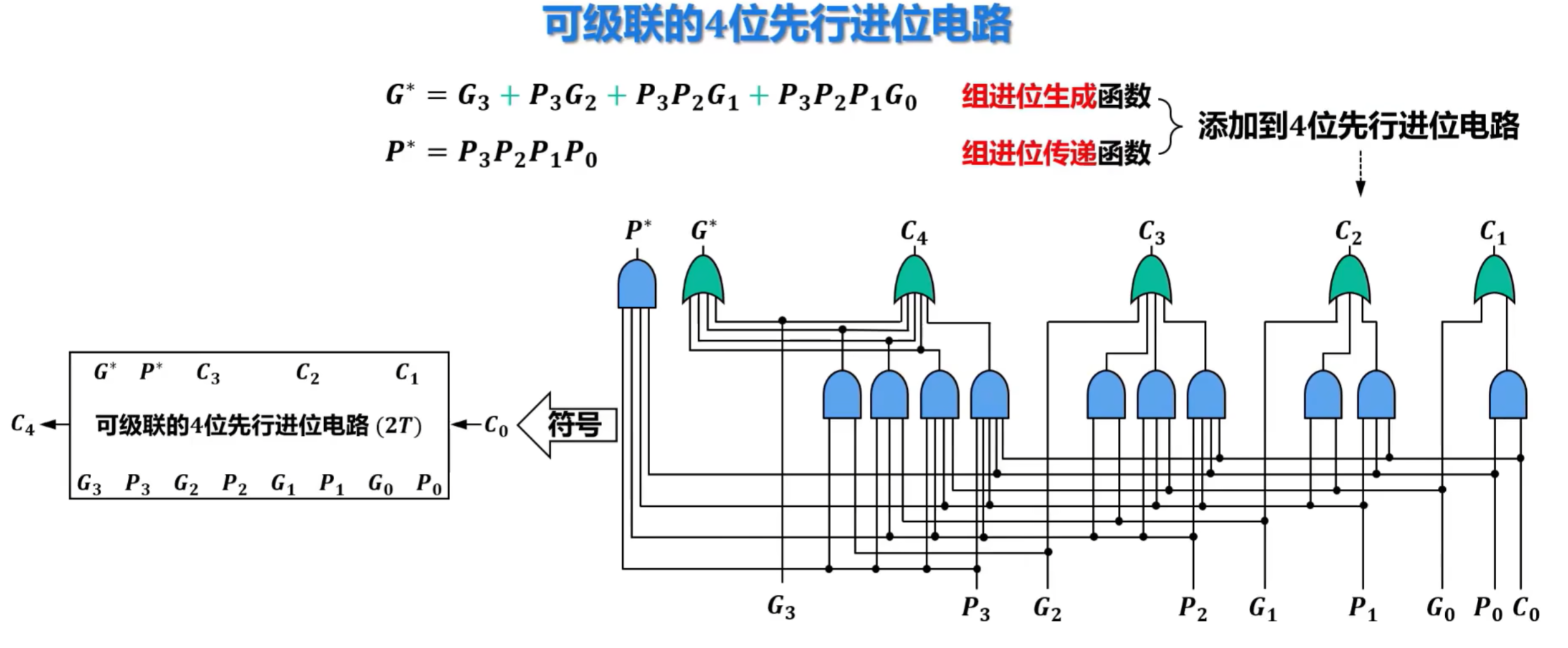
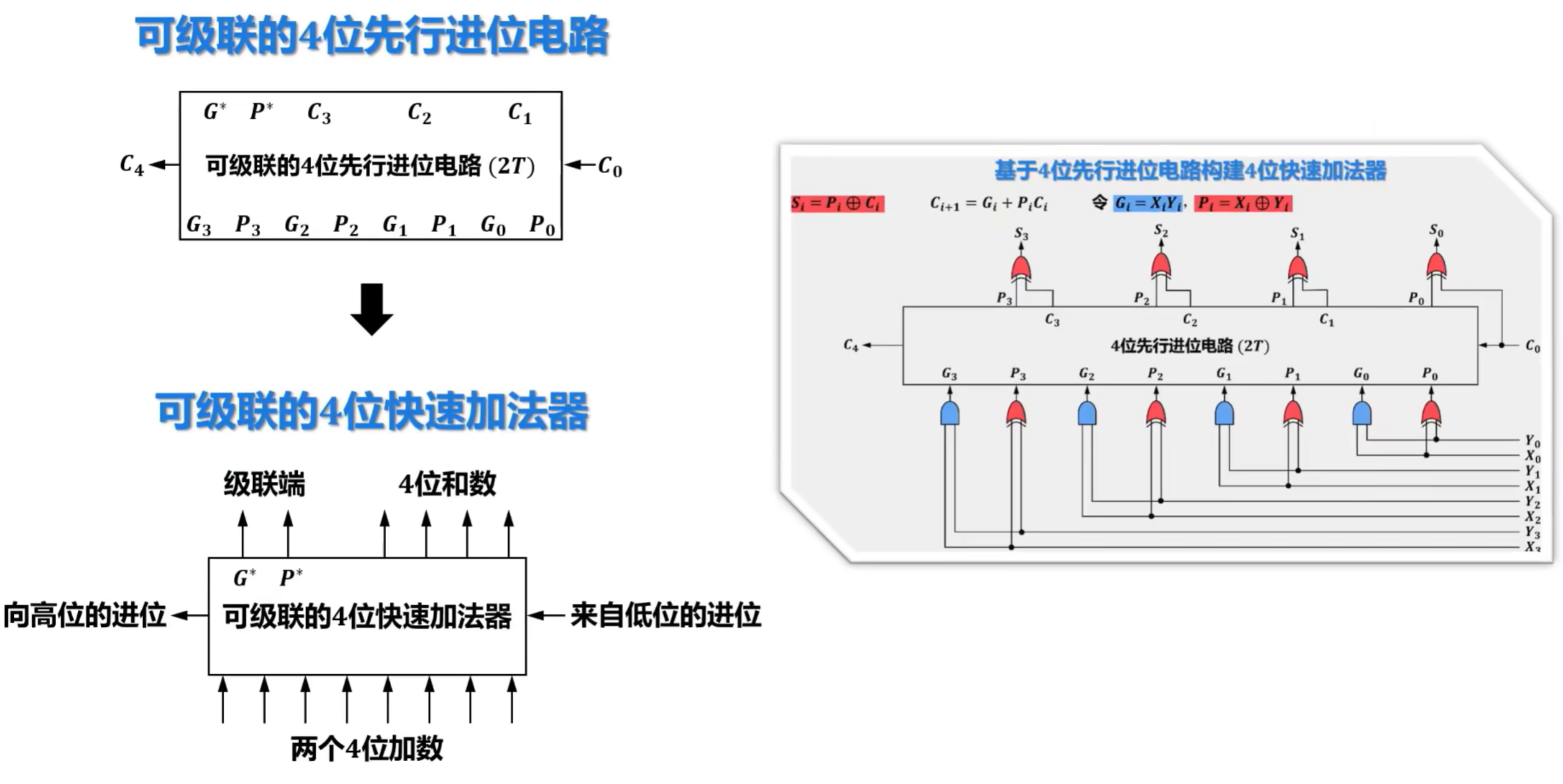
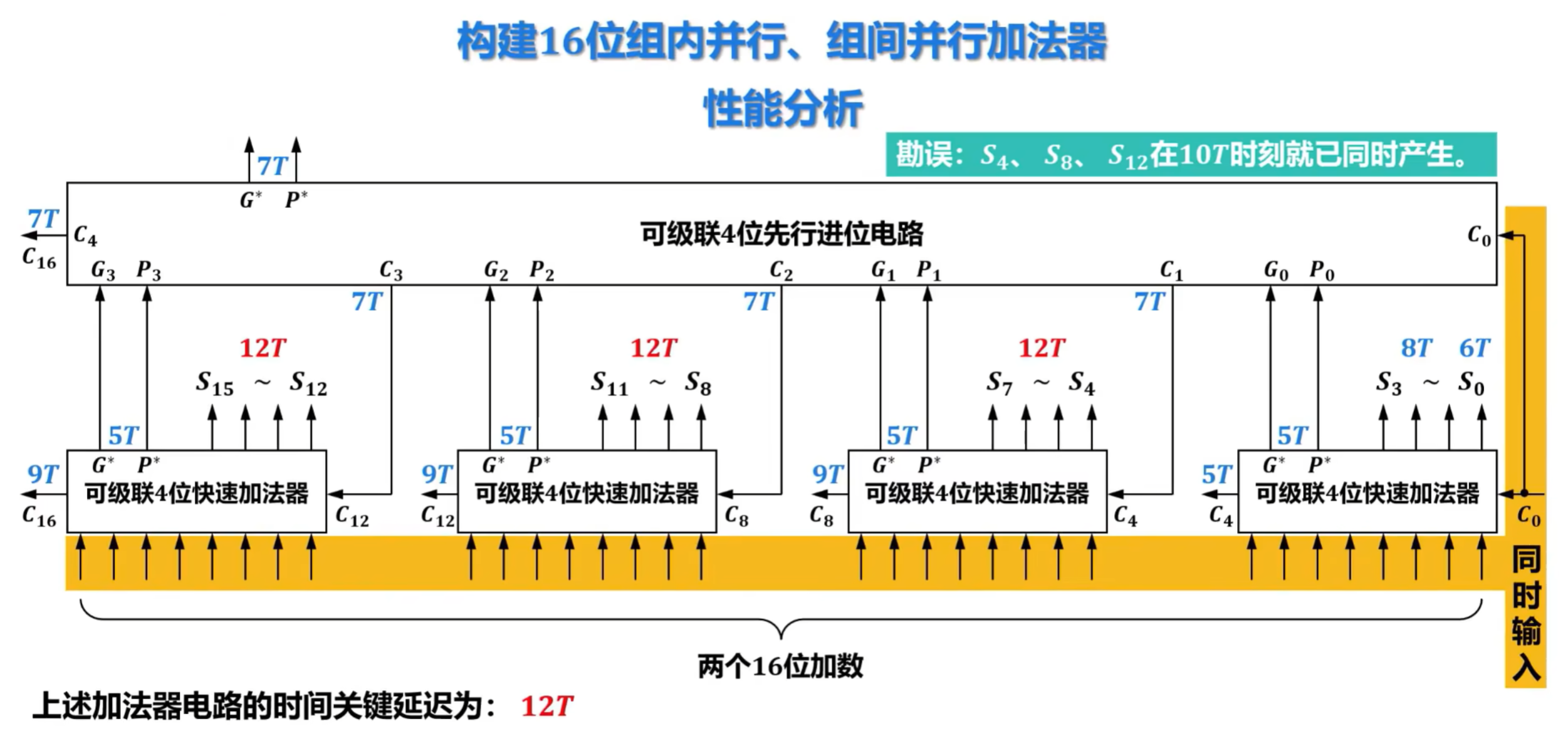
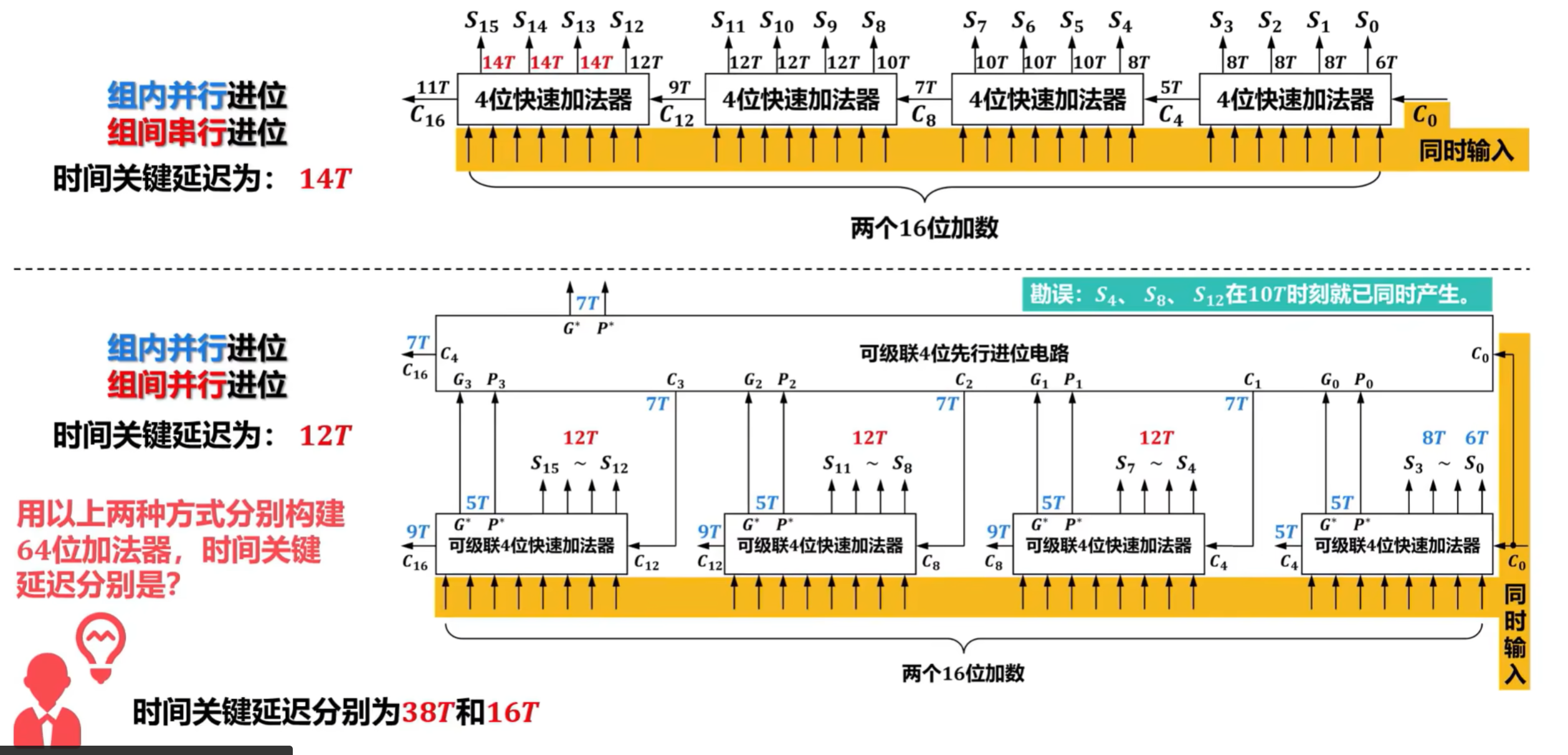
3、定点数的乘除运算
1)无符号数乘法运算的硬件逻辑实现
需要一个位宽为4位的寄存器存放被乘数x;还需要两个位宽为4位的寄存器分别存放部分积和最终乘积的高位和低位,初始阶段高位寄存器被清0,低位寄存器存放乘数y。再配上加法器及其他相应电路,即可实现乘法运算。
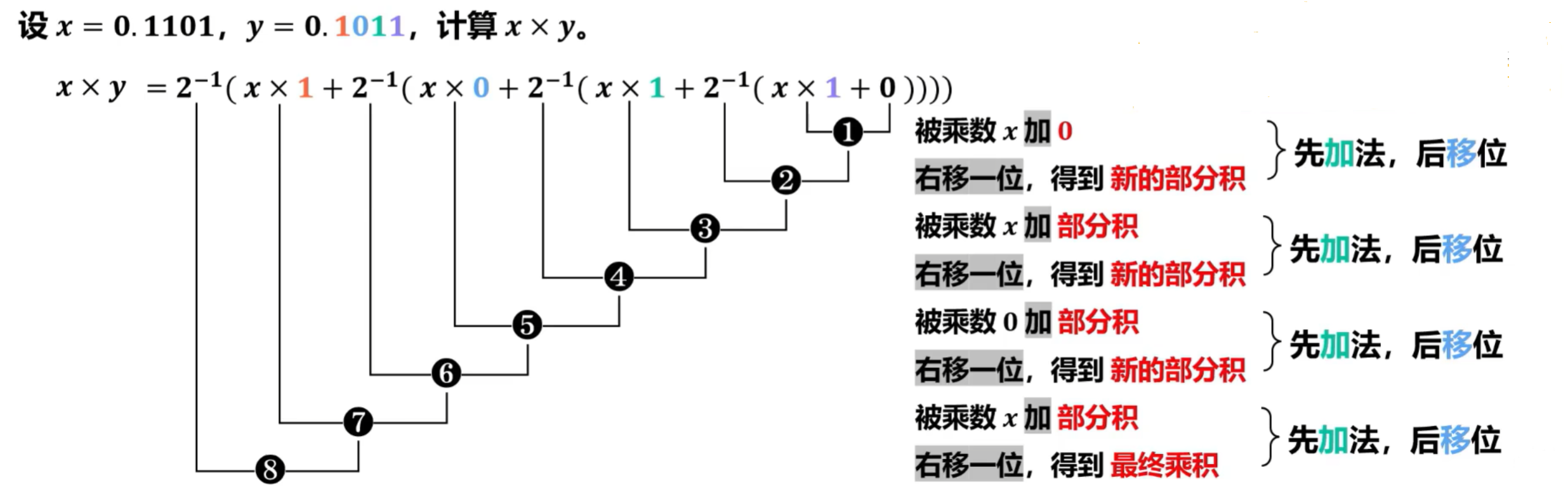

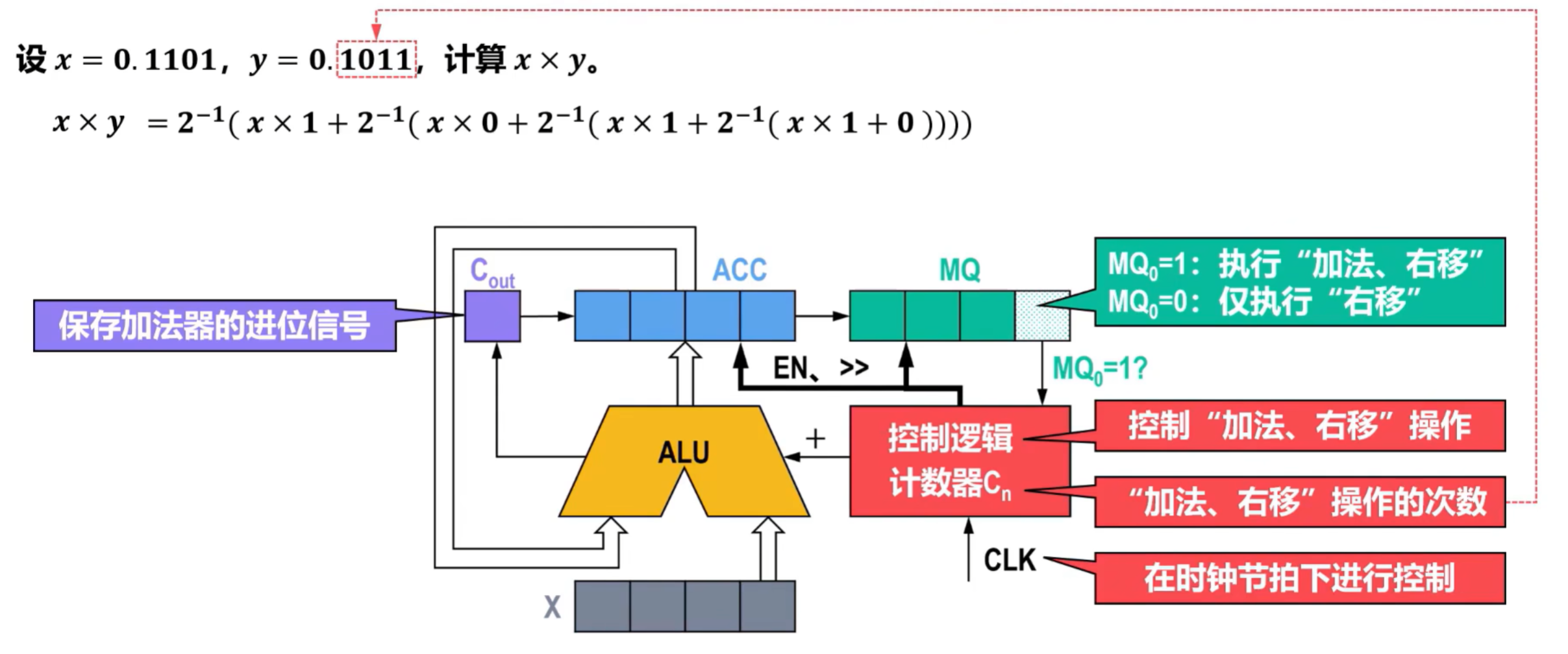
乘法的过程图例:
- 初始化,将x作为被乘数放入到ALU中,乘数放入MQ中,计数器设置为4,因为被乘数小数点后有4位;
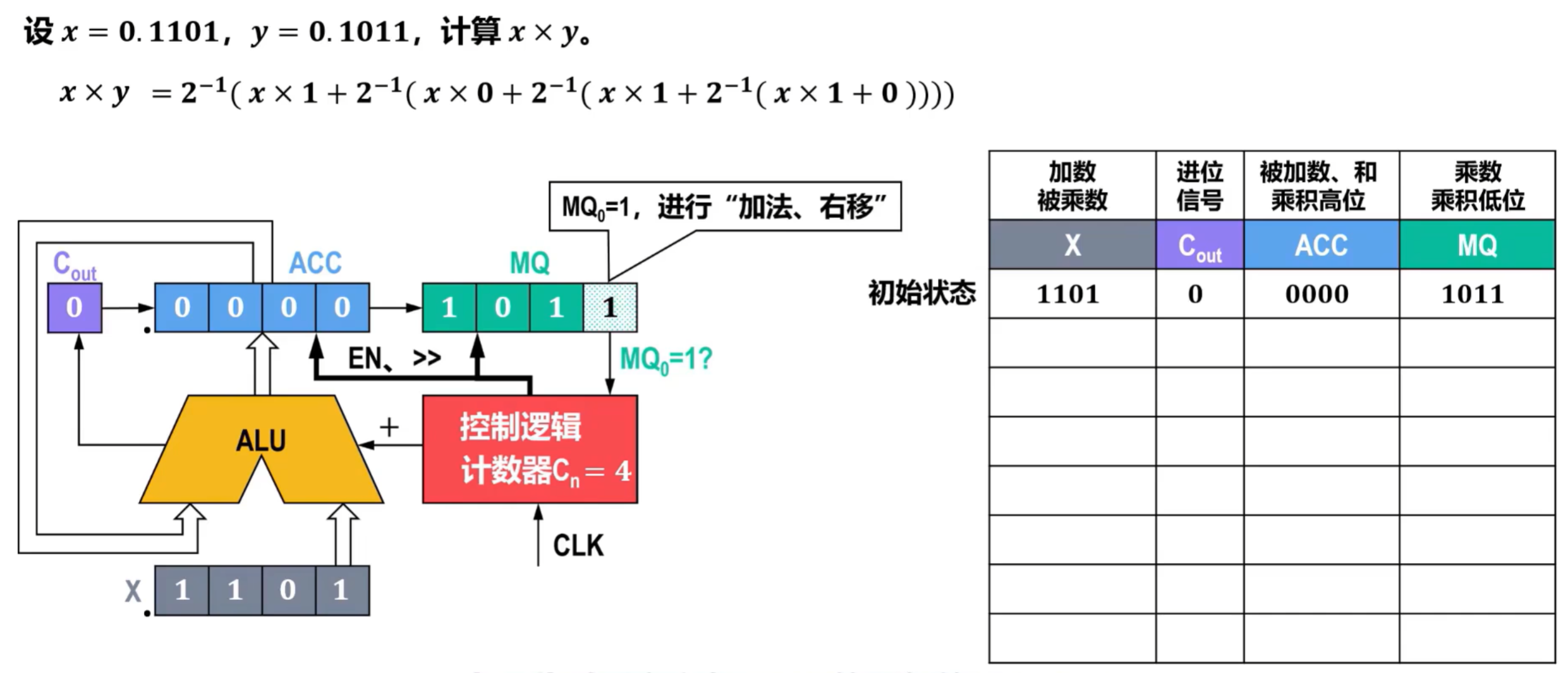
- ACC初始化为0000,将ACC和X放入ALU进行相加,并将结果放入ACC中,相加过程中未产生进位,Cout为0;
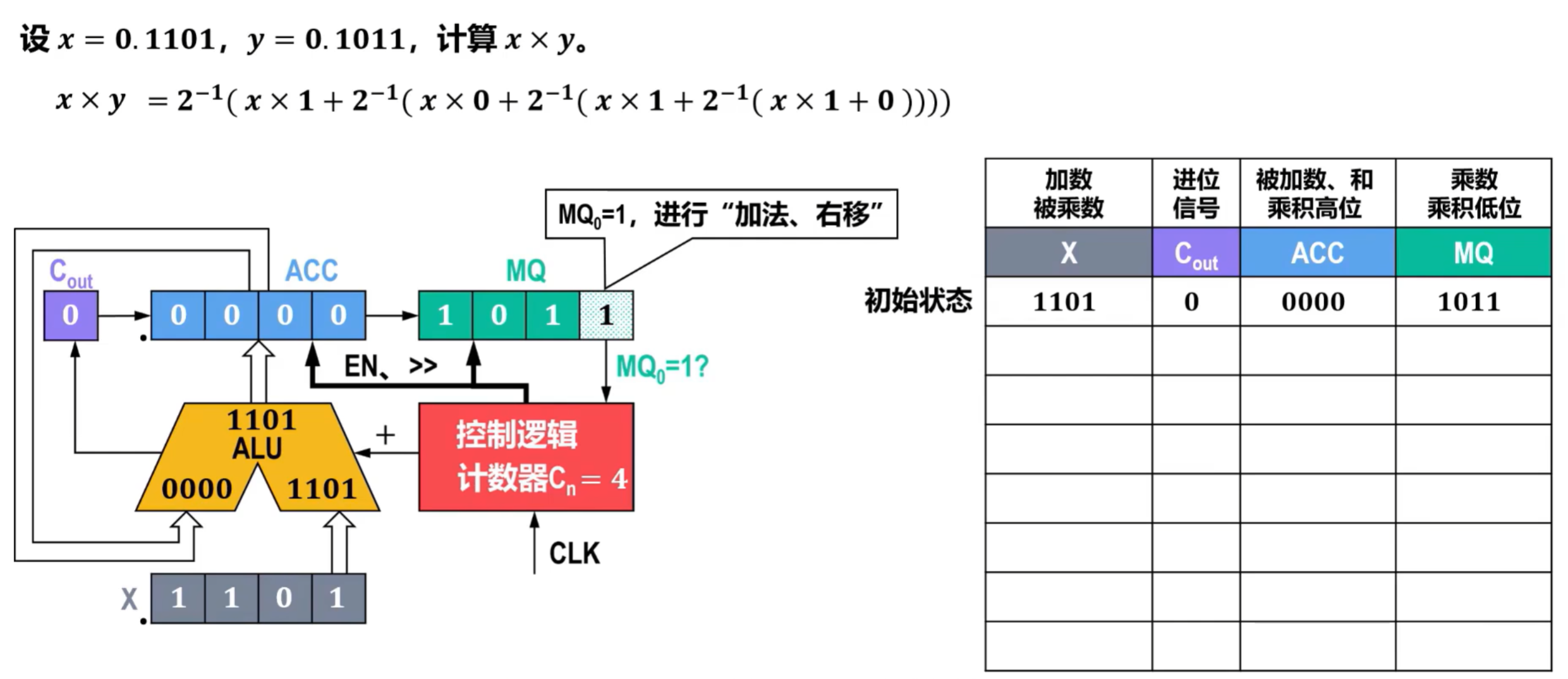
- 将刚刚的结果放入回ACC中,并记录,此时最右侧的表达式已完成计算;
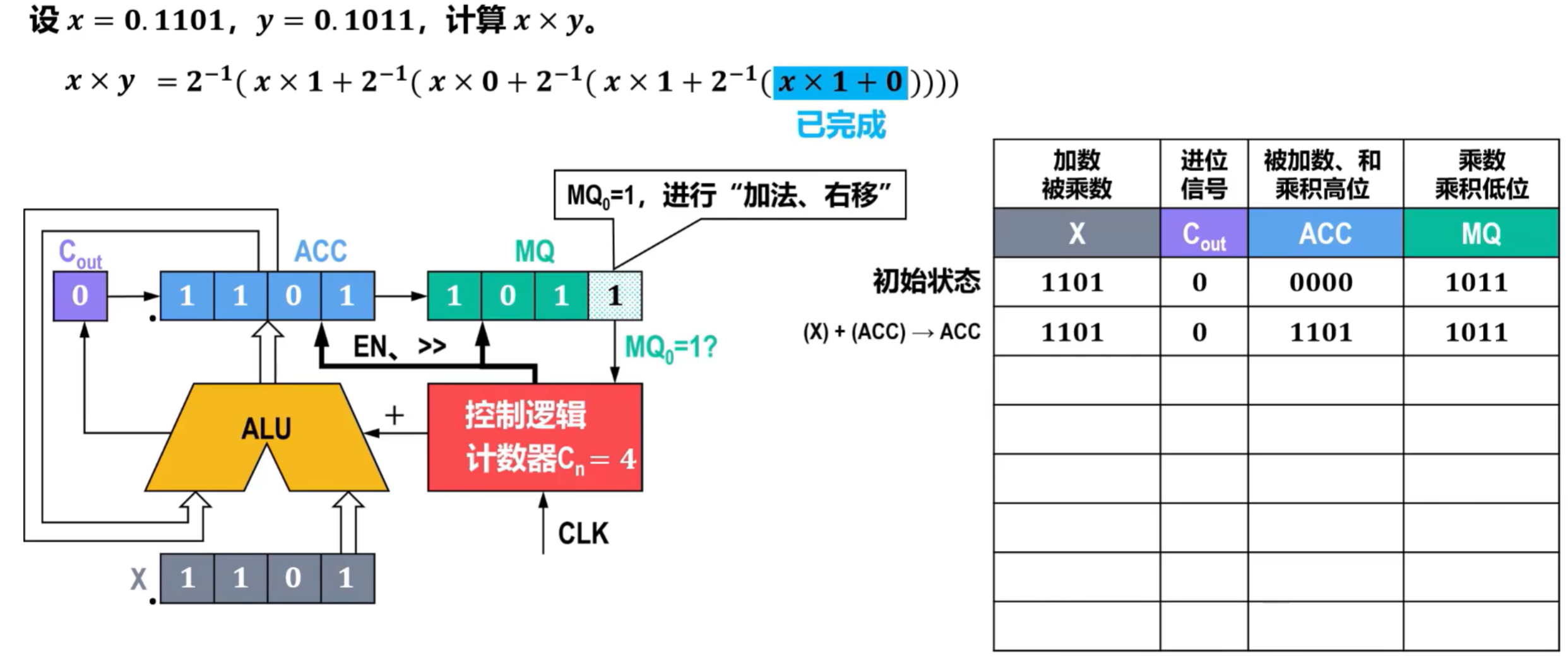
- 此时需要将Cout、ACC和MQ进行右移,完成2-1的操作,右移得到的数舍弃,即MQ右移后在外的数舍弃,并记录到右侧表格中,此时表达式右侧的第一个表达式已完成,将计数器Cn设置为3;
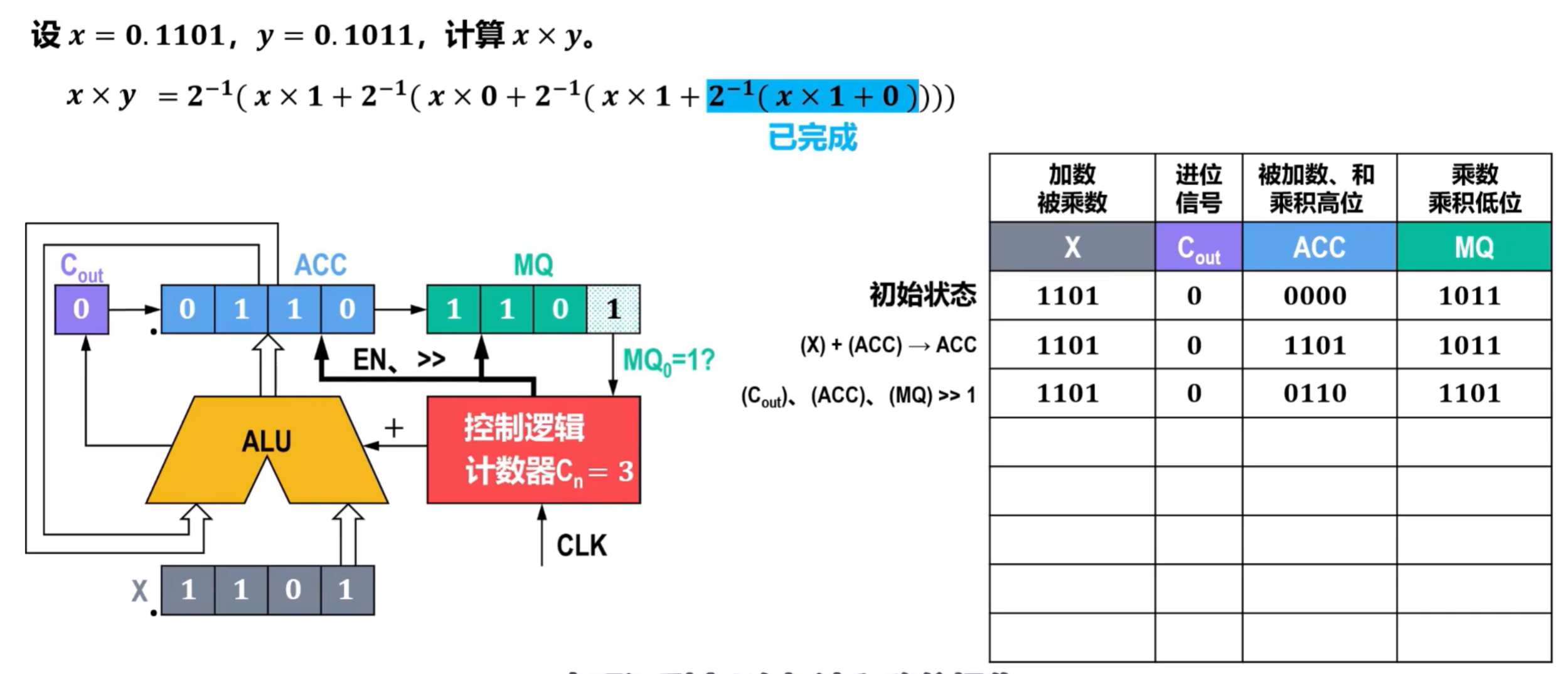
- 将ACC和X放入ALU中进行相加,得到的数放回ACC中,相加过程中产生进位1,放入到进位器Cout中,如图所示;
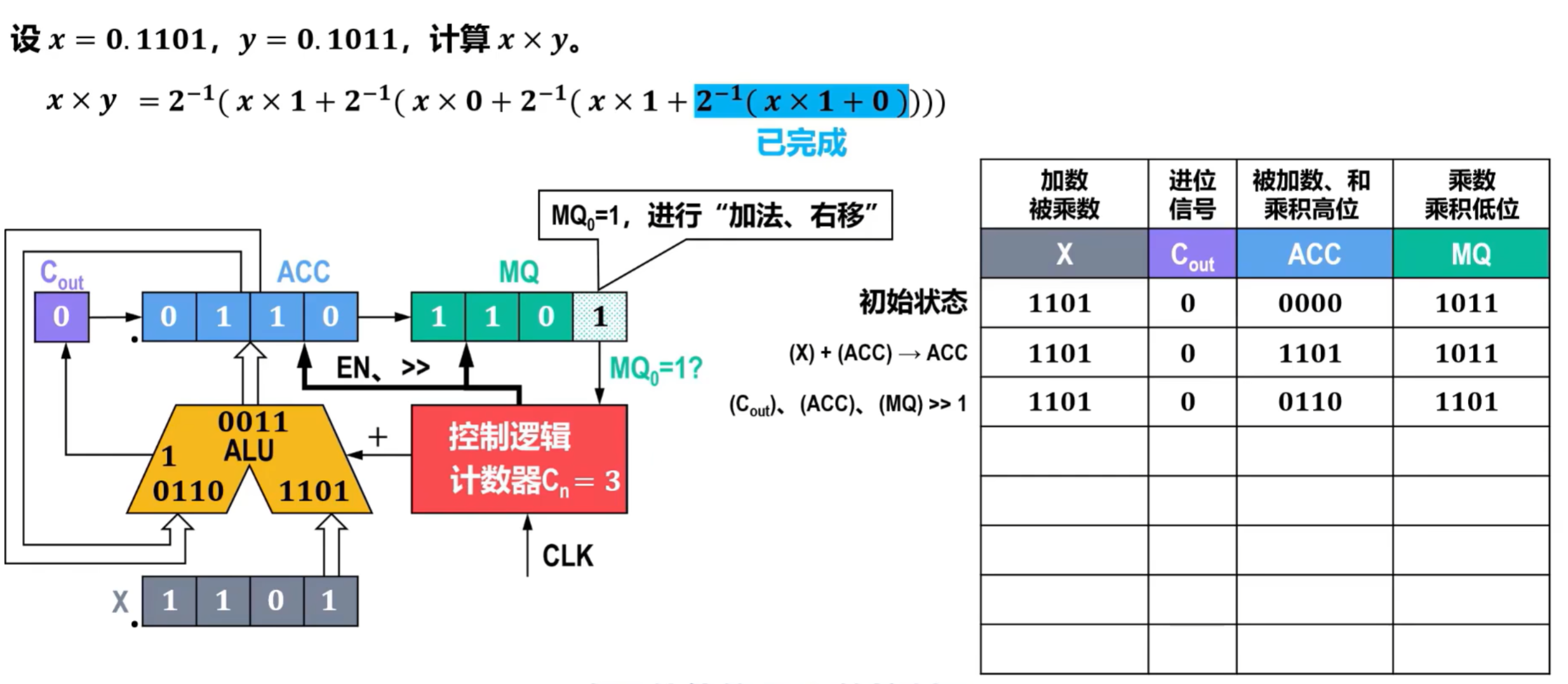
- 右移,完成表达式中最右侧第二个表达式,Cout补0,属于逻辑移位,记录在表格中,计数器Cn更新为2;
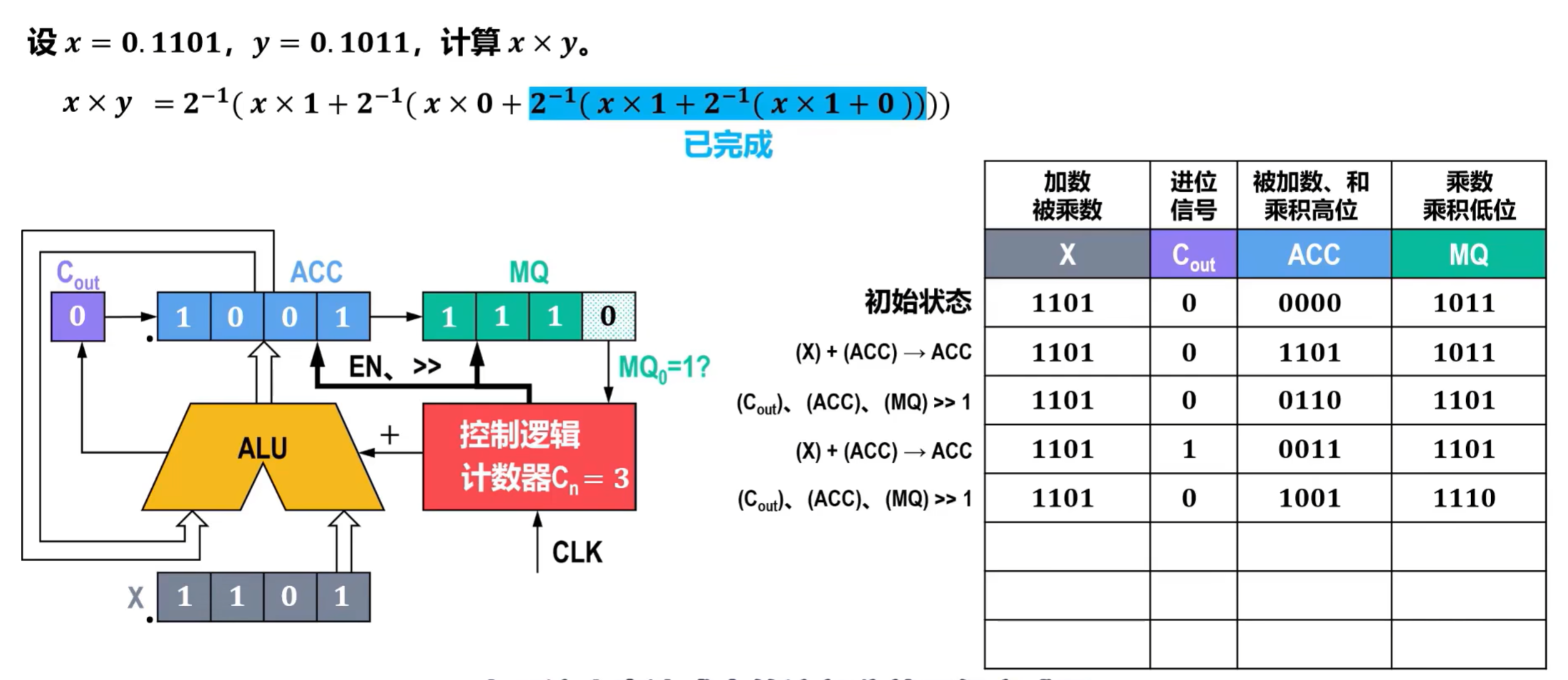
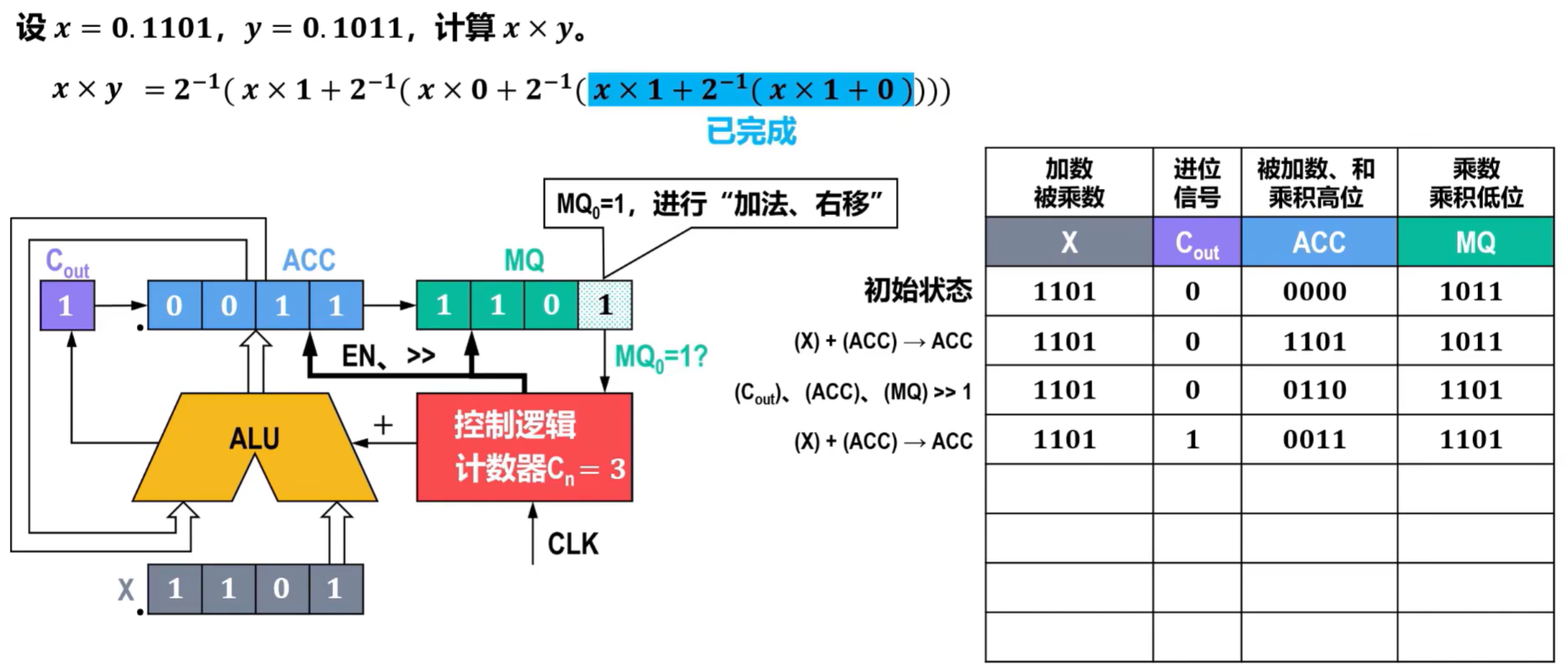
- 以此类推,如果MQ的最后一位为0,则只需要右移即可,不需要进行X和ACC的累加,进位器补0,得到最终结果如下,其中,ACC的最终内容为结果的最高位,MQ为结果的最低位。
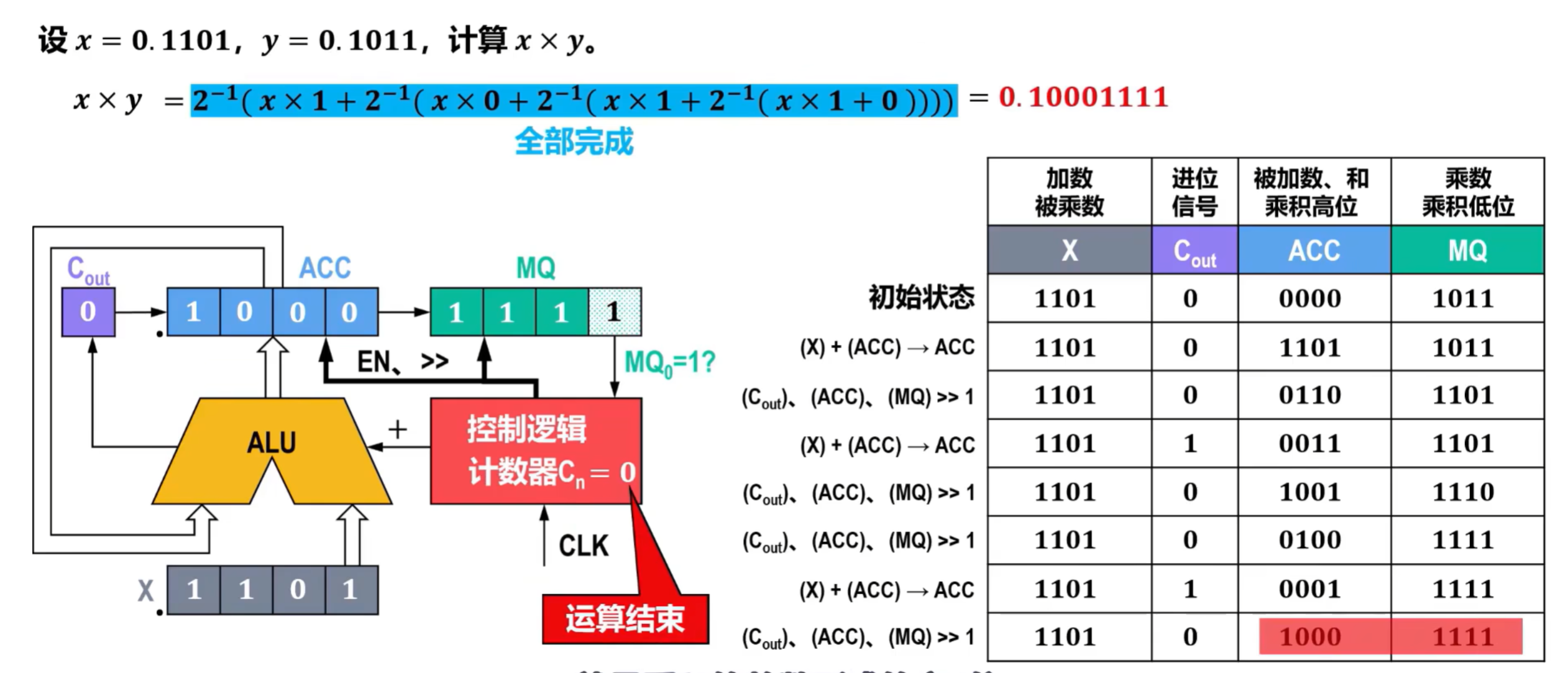
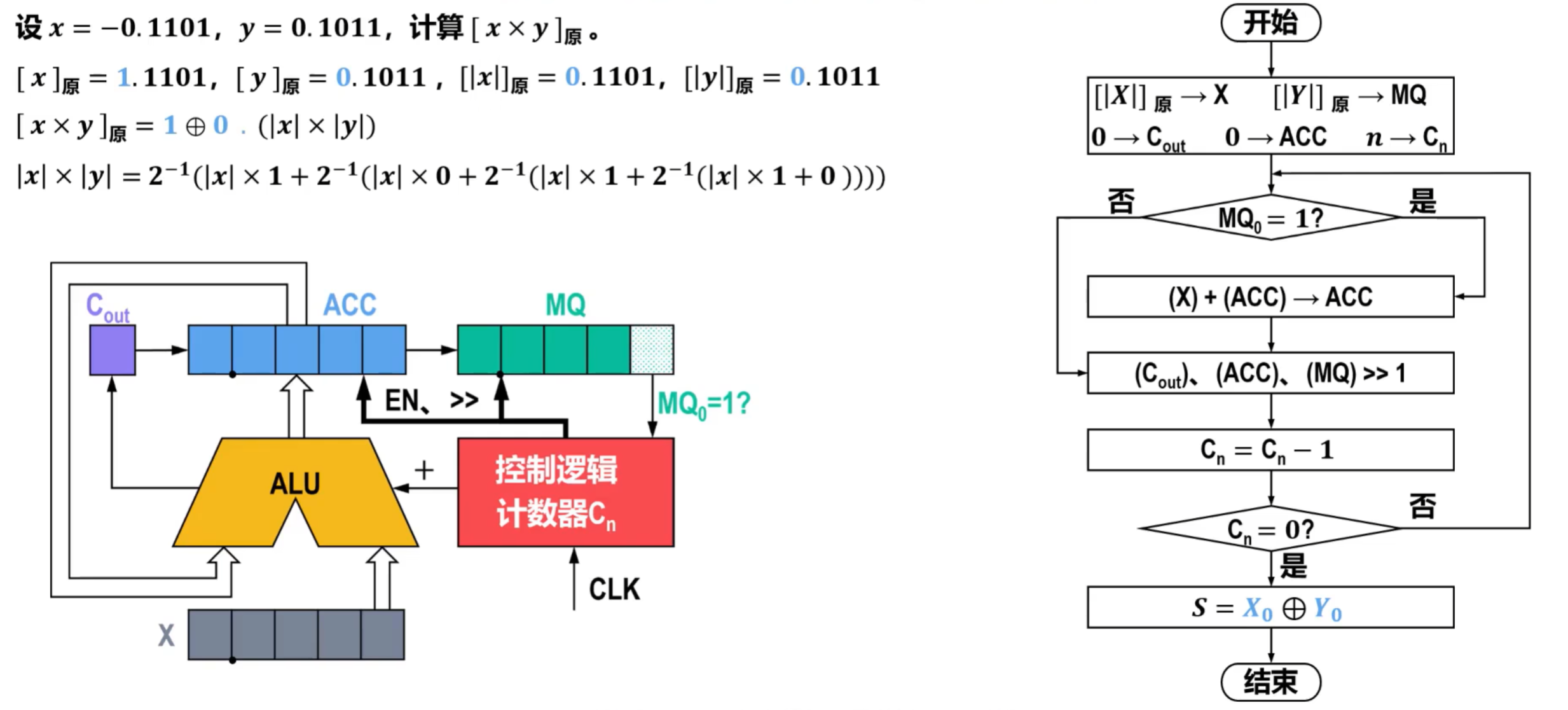
2)原码乘法运算的硬件逻辑实现
由于原码表示与无符号数非常类似,仅比无符号数多一个符号,而乘积的符号可以通过参与运算的两个数各自符号的逻辑异或求得,因此,上述无符号数乘法运算的硬件逻辑实现,可用于原码一位乘法仅需添加符号位处理即可。
- 原码一位乘法运算的硬件逻辑实现

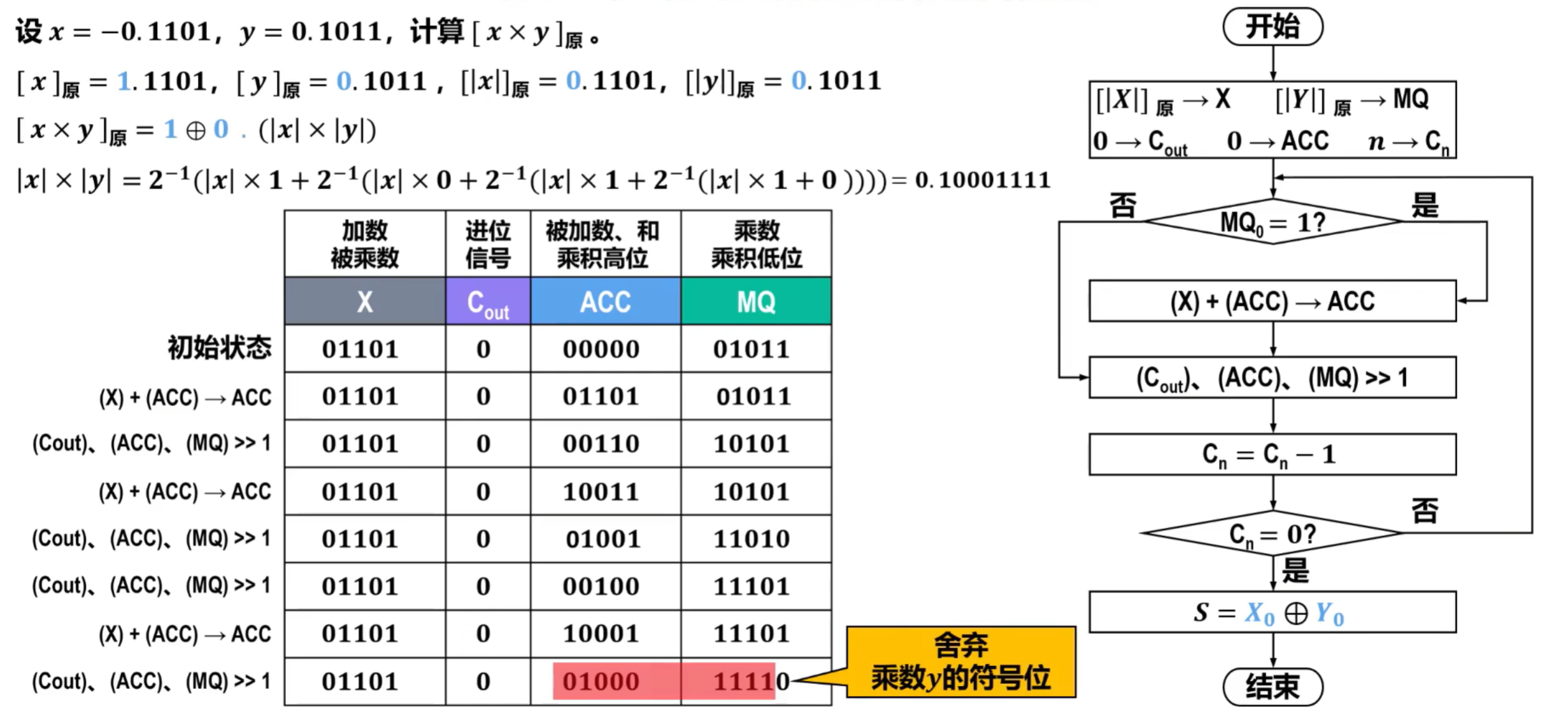
- 假设使用5位寄存器,计算x和y原码的乘积,小数点默认在第一位数的后面,电路图如下,右图为流程图;
- 按照无符号数乘法运算,得到原码乘法运算的结果如下:
3)补码乘法运算的硬件逻辑实现
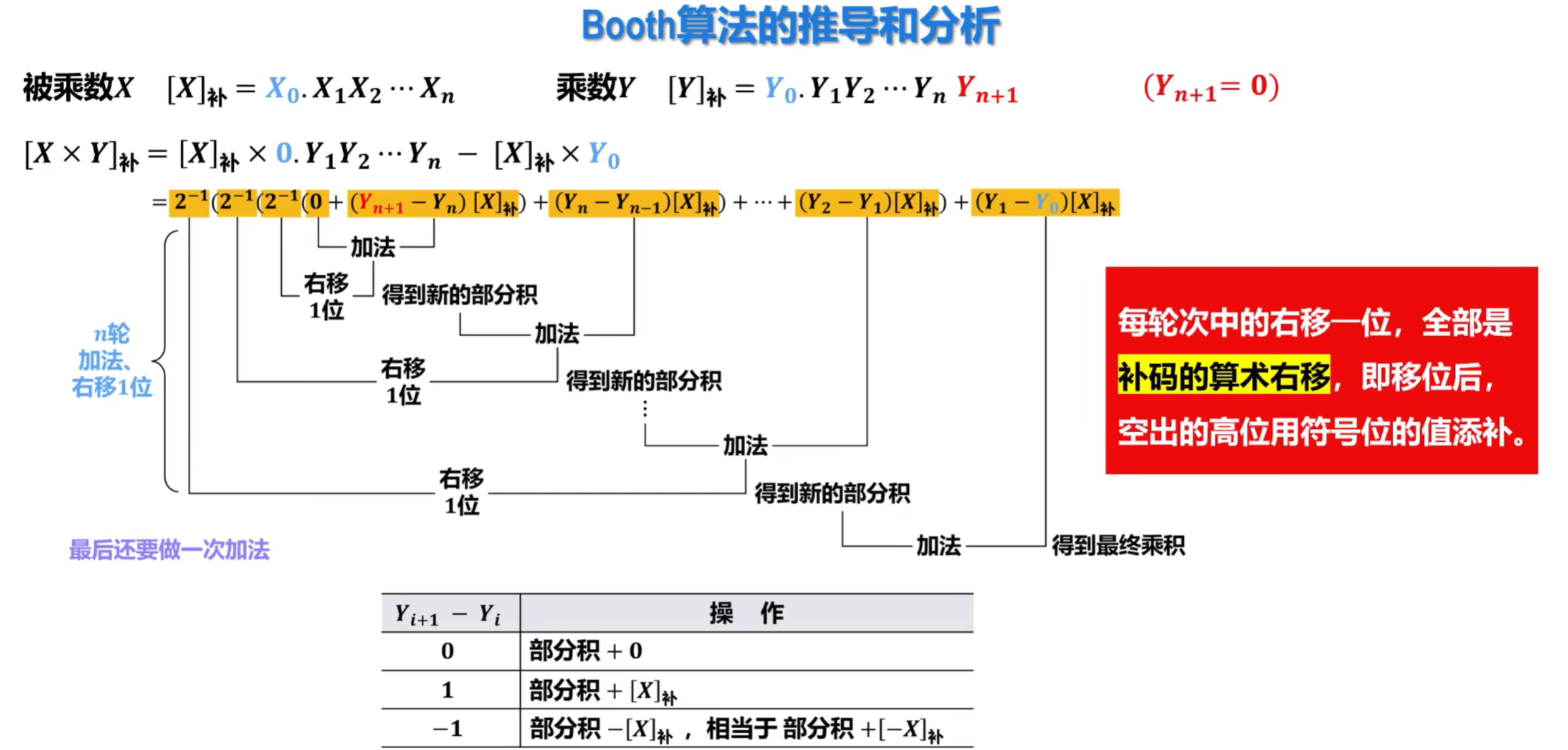
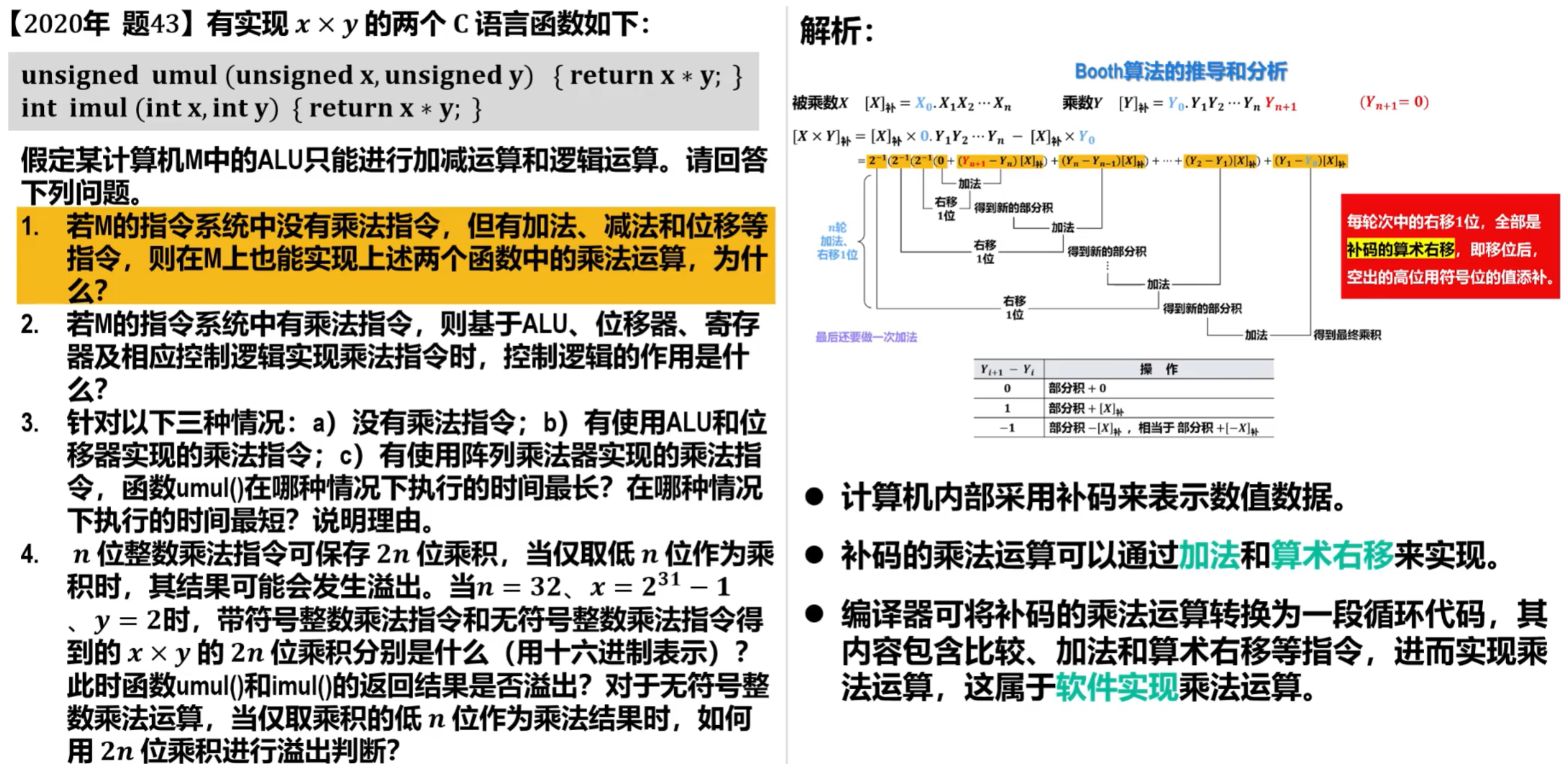
由于计算机中采用补码表示数据,如果用原码乘法计算两个数的乘积,则运算前需要将补码转换为原码、运算后还需要将原码再转换为补码,这样会增加许多操作步骤。为了减少处理环节,英国的布斯(Booth)夫妇于1950年提出了一种补码乘法,又称为Booth算法。
①Booth算法的推导和分析


- 记住两个公式和Yi+1-Yi的操作即可
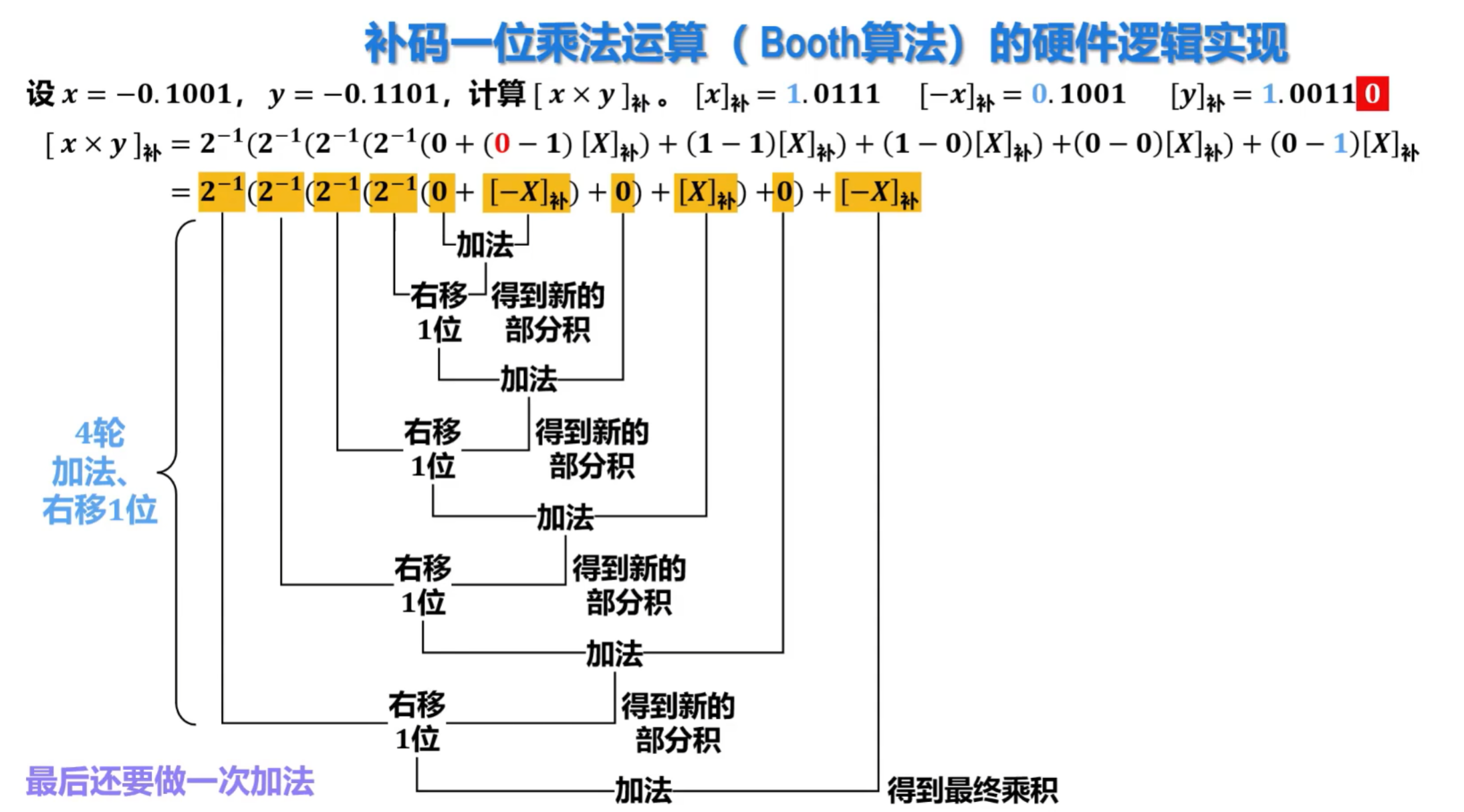
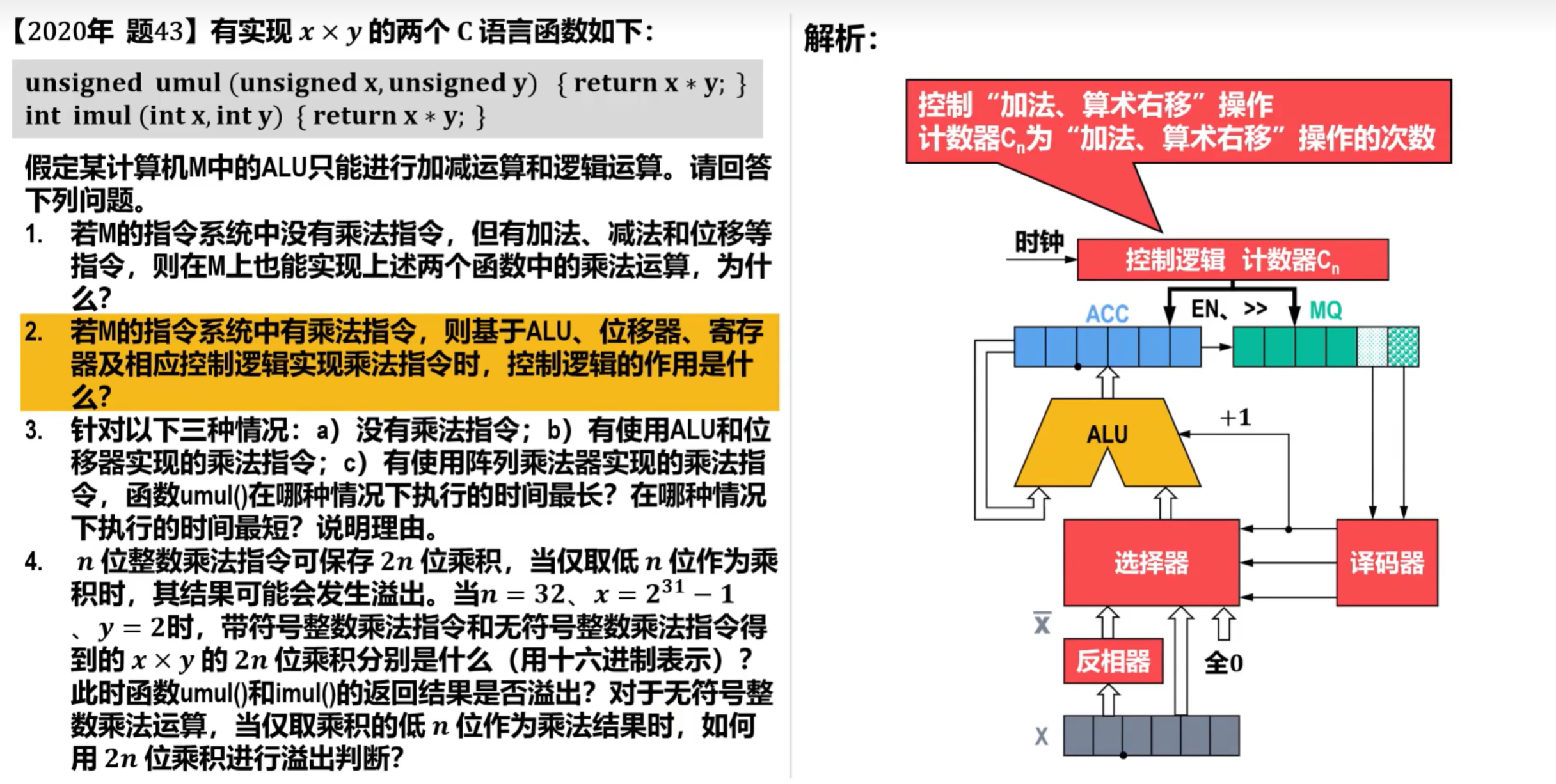
②补码一位乘法运算(Booth算法)的硬件逻辑实现
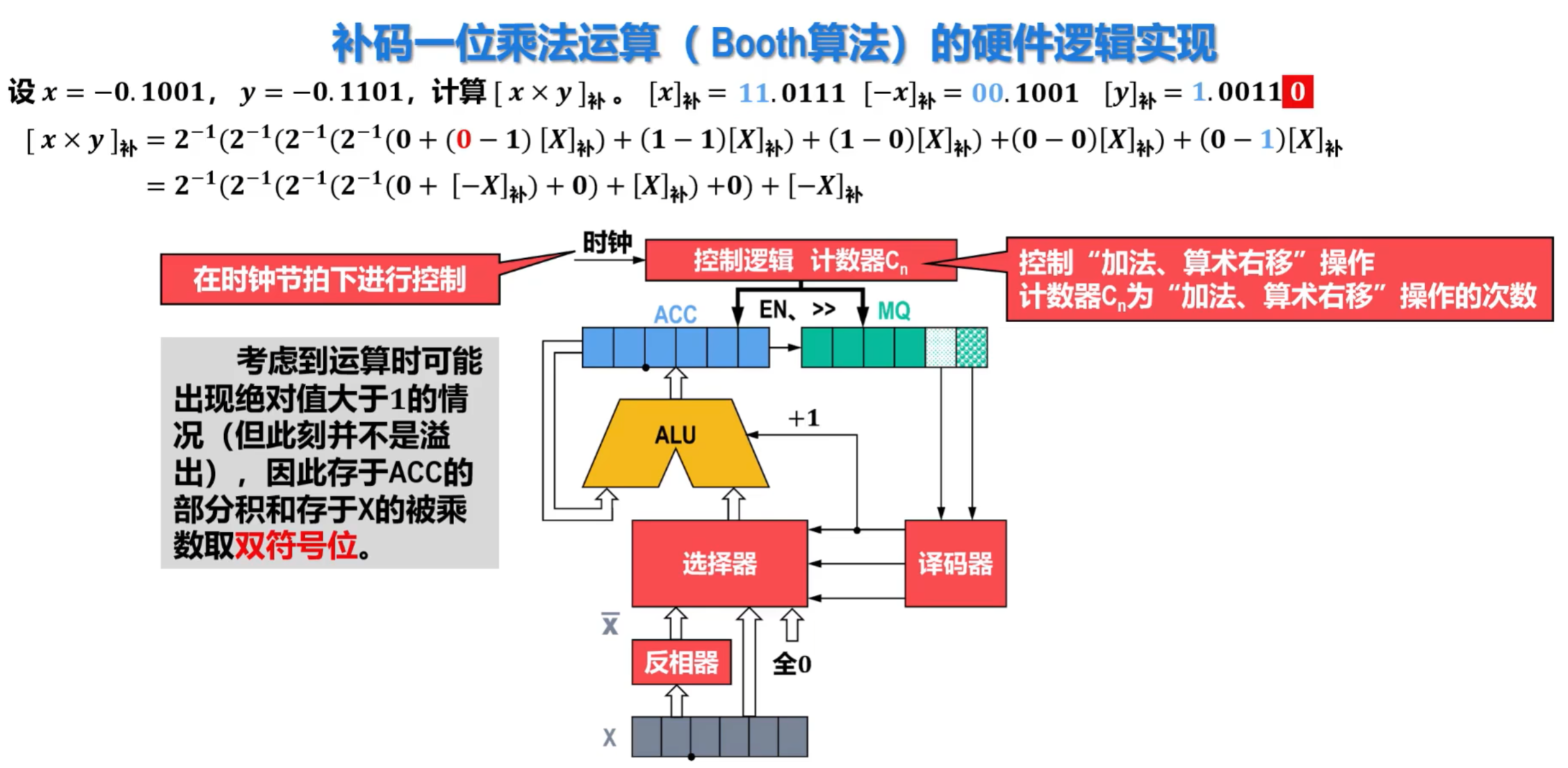
- 其中,对译码器进行解释:
- Yi+1-Yi都为0,译码器结果为1,将全0输出给ALU
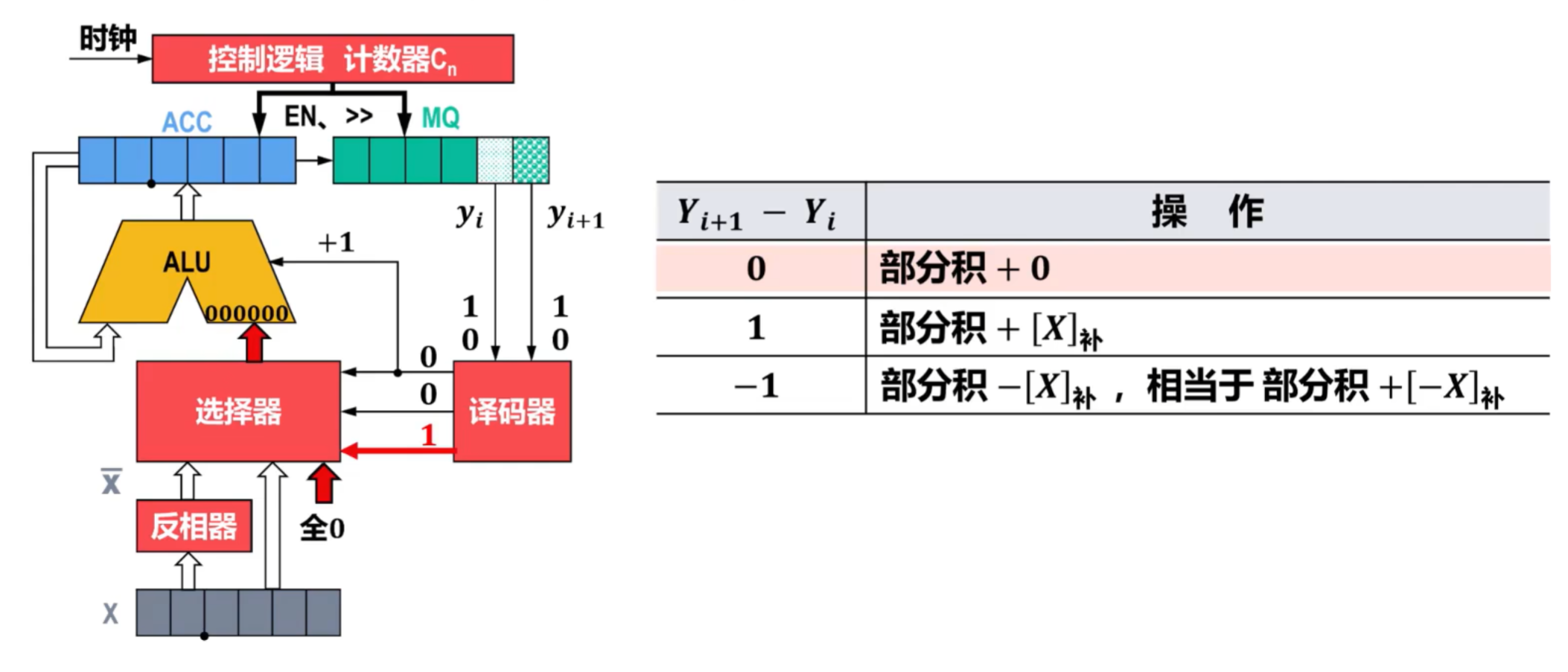
- Yi+1-Yi分别为1和0,译码器结果为1,将X输出到ALU,即X的补码
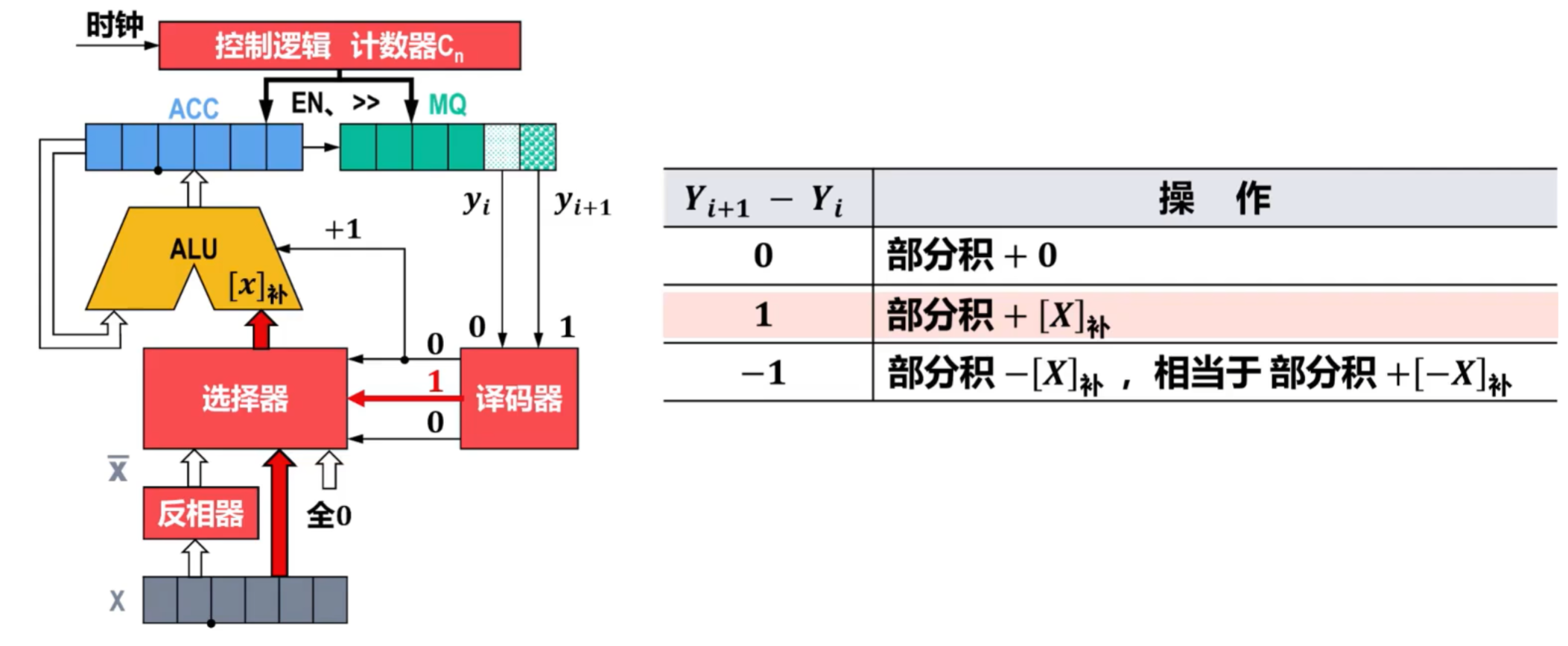
- Yi+1-Yi分别为0和1,译码器结果为0,将X的补码输出到ALU并+1
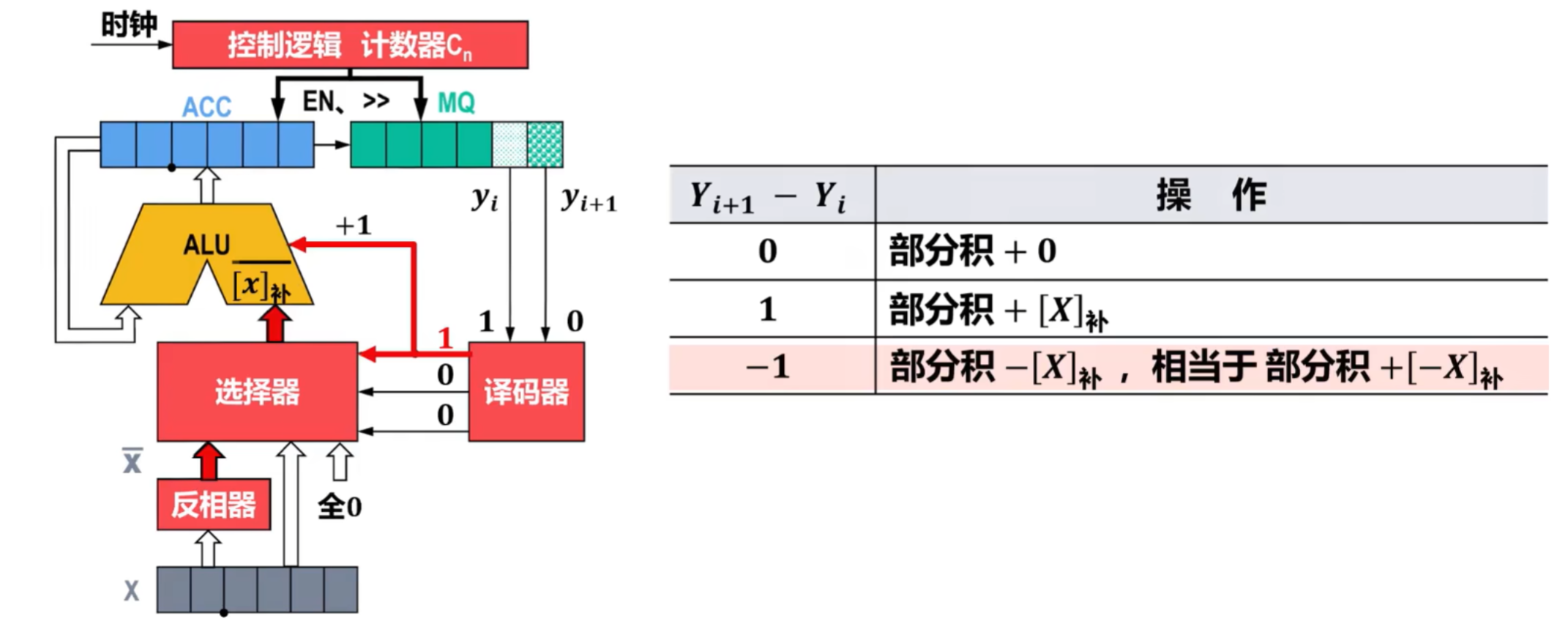
- 执行流程图如下:
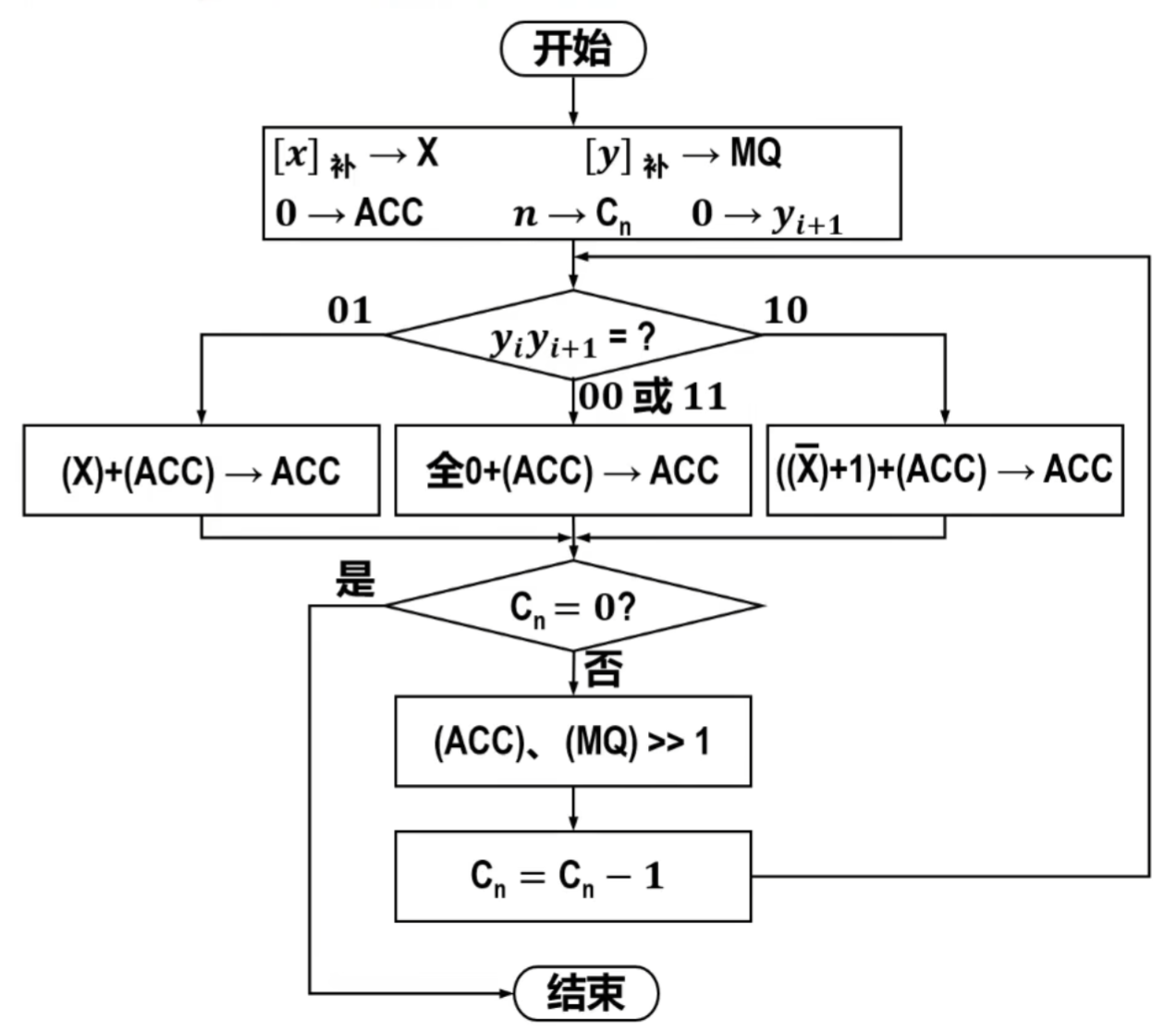
- 根据流程图,得到的结果如下:
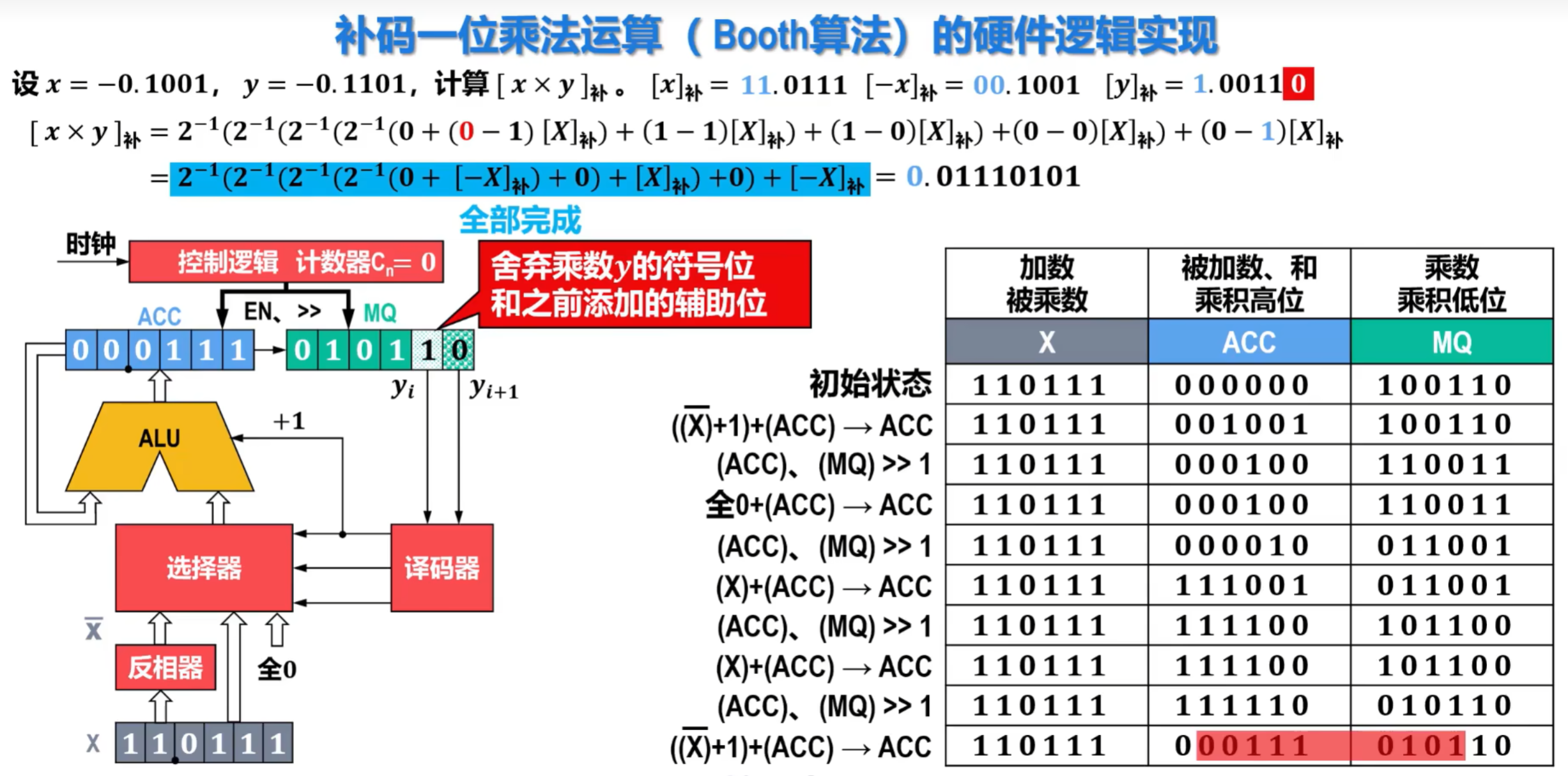
③例题
题1:


题2:


Booth算法也适用于定点整数的补码运算;
为了提高乘法的运算速度,可采用补码二位乘法。
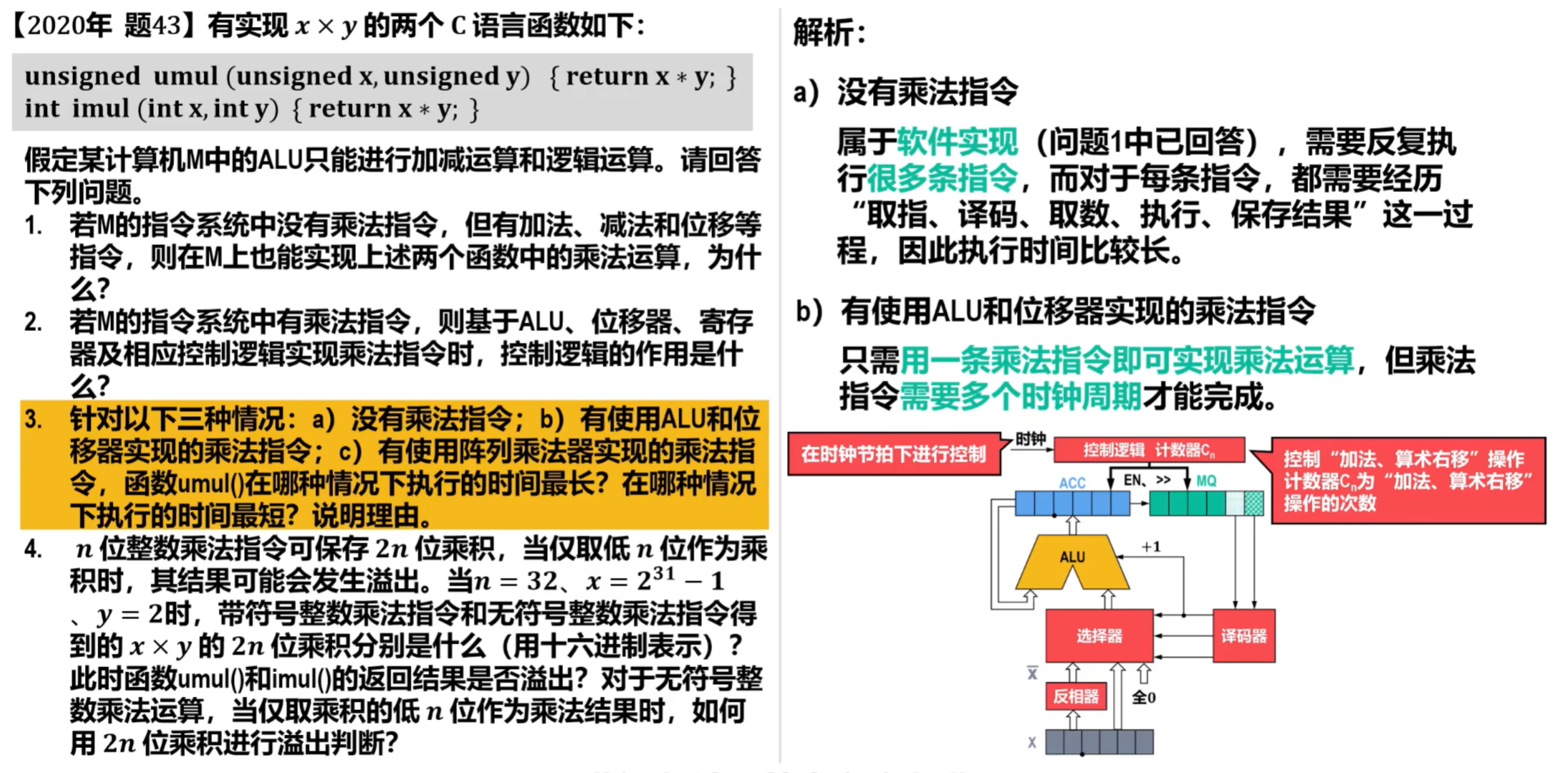
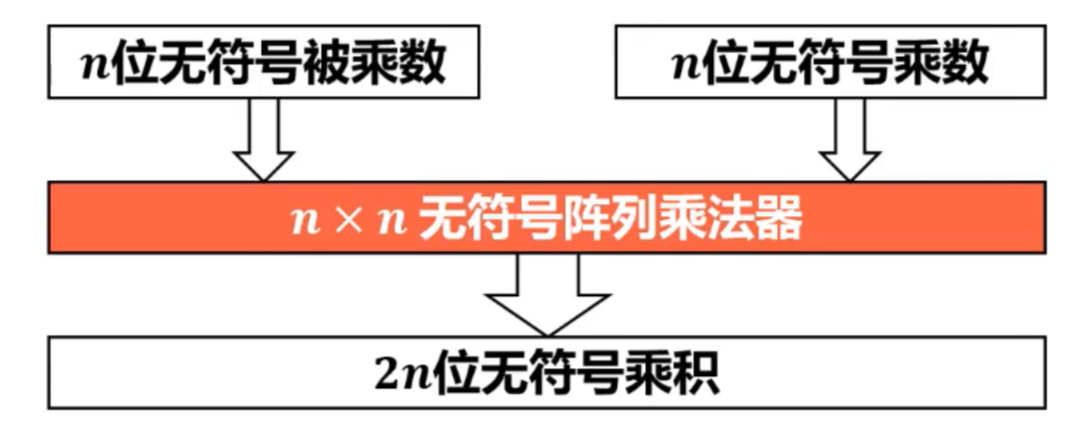
4)无符号阵列乘法器
- 原码、补码一位乘法的硬件逻辑实现,需要在时钟节拍下、通过控制逻辑的控制,执行相应轮次的“ 加法 、右移 ”操作来实现,速度较慢;
- 为了提高运算速度,可以仅采用组合逻转电路以专用硬件方式构建阵列乘法器;
- 构建阵列乘法器的基本思想是模仿二进制乘法的笔算方法。
- 二进制乘法的笔算方法

- 将每个得到的乘积用逻辑与包含进行运算
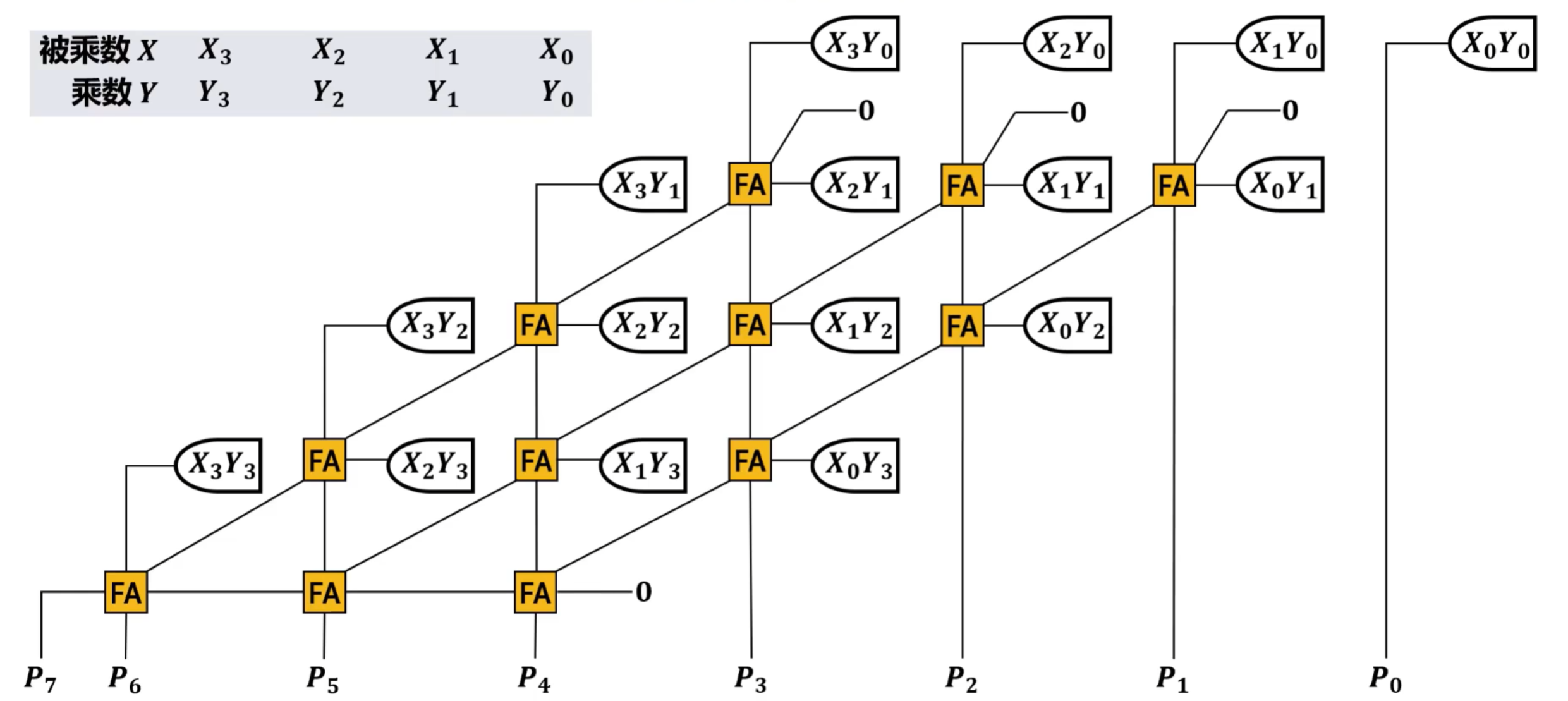
- 假设X和Y的数值后,标记Xi和Yi的数值,并计算,FA为全加器,加法输出即为Pi。
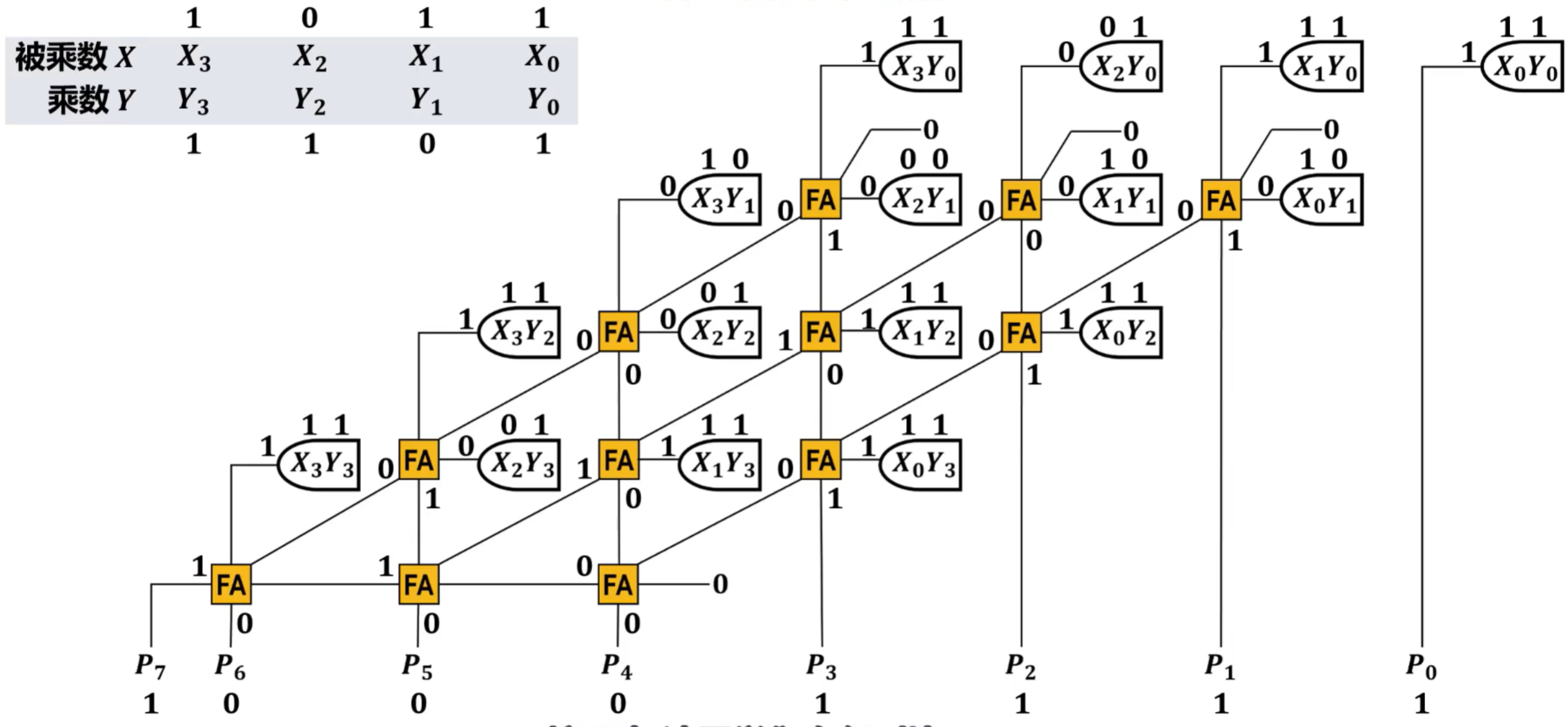
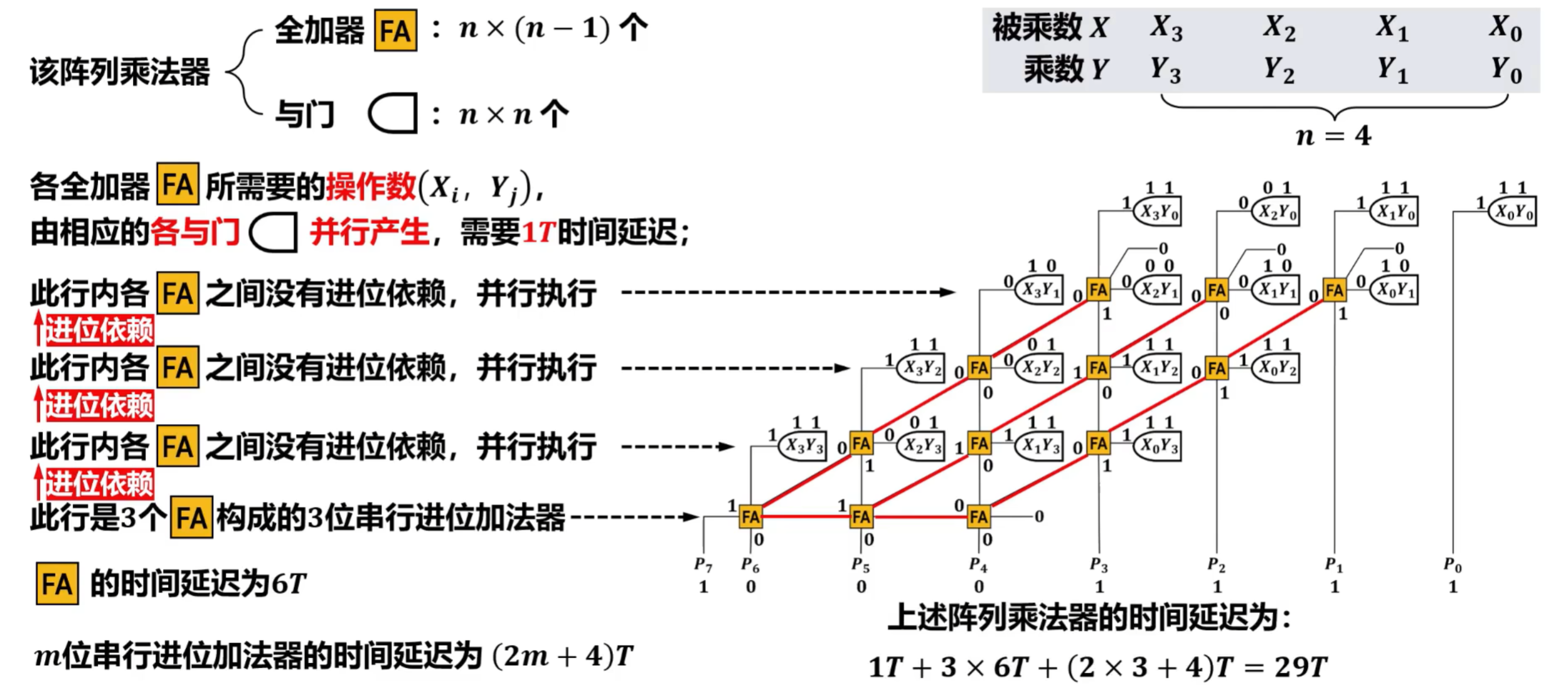
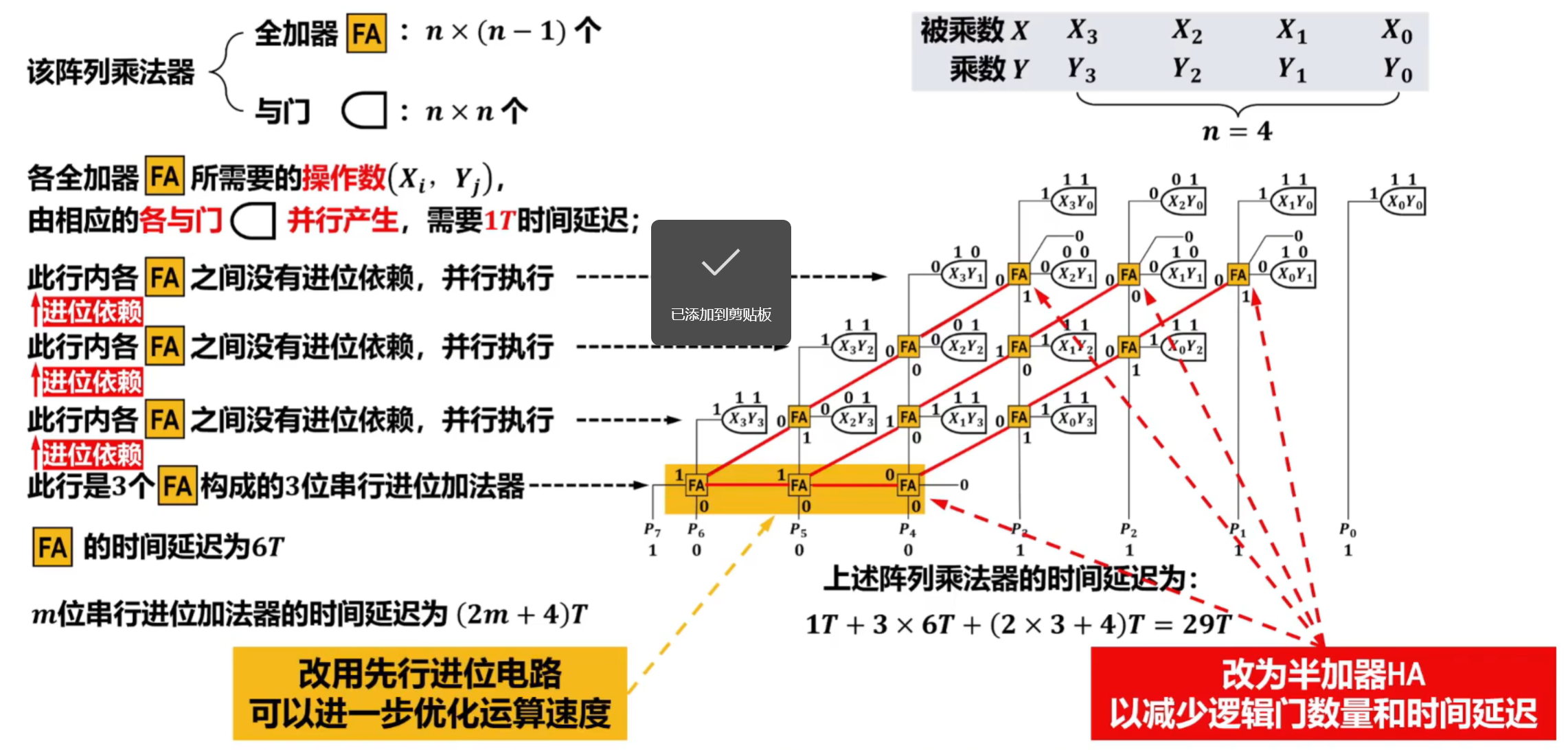
阵列乘法器结构规范标准化程度高,有利于布局布线,适合用超大规模集成电路实现,且可以获得较高的运算速度,其运算速度仅取决于逻辑门和加法器的传输延迟。
5)补码阵列乘法器
由于计算机中采用补码表示数据,因此,设法基于无符号阵列乘法器设计补码阵列乘法器
- 如果不考虑原码的符号位,则原码的数值位可看作是无符号数
- 如果将原码的符号位单独处理,则原码乘法运算,可将被乘数原码的数值位和乘数原码的数值位直接代入无符号阵列乘法器进行运算;
- 得到的结果为无符号乘积,在其前面添加单独处理的符号位,即可得到原码乘法的结果。
- 原码与补码之间可以相互转换,可采用反码法或扫描法
- 如果将补码的符号位单独处理,将补码的数值位转换成原码的数值位,就可利用无符号阵列乘法器进行乘法运算;
- 得到的结果为无符号乘积,将其转换成补码的数值位,然后在其前面添加单独处理的符号位,即可得到补码乘法的结果。
- 补码阵列乘法器
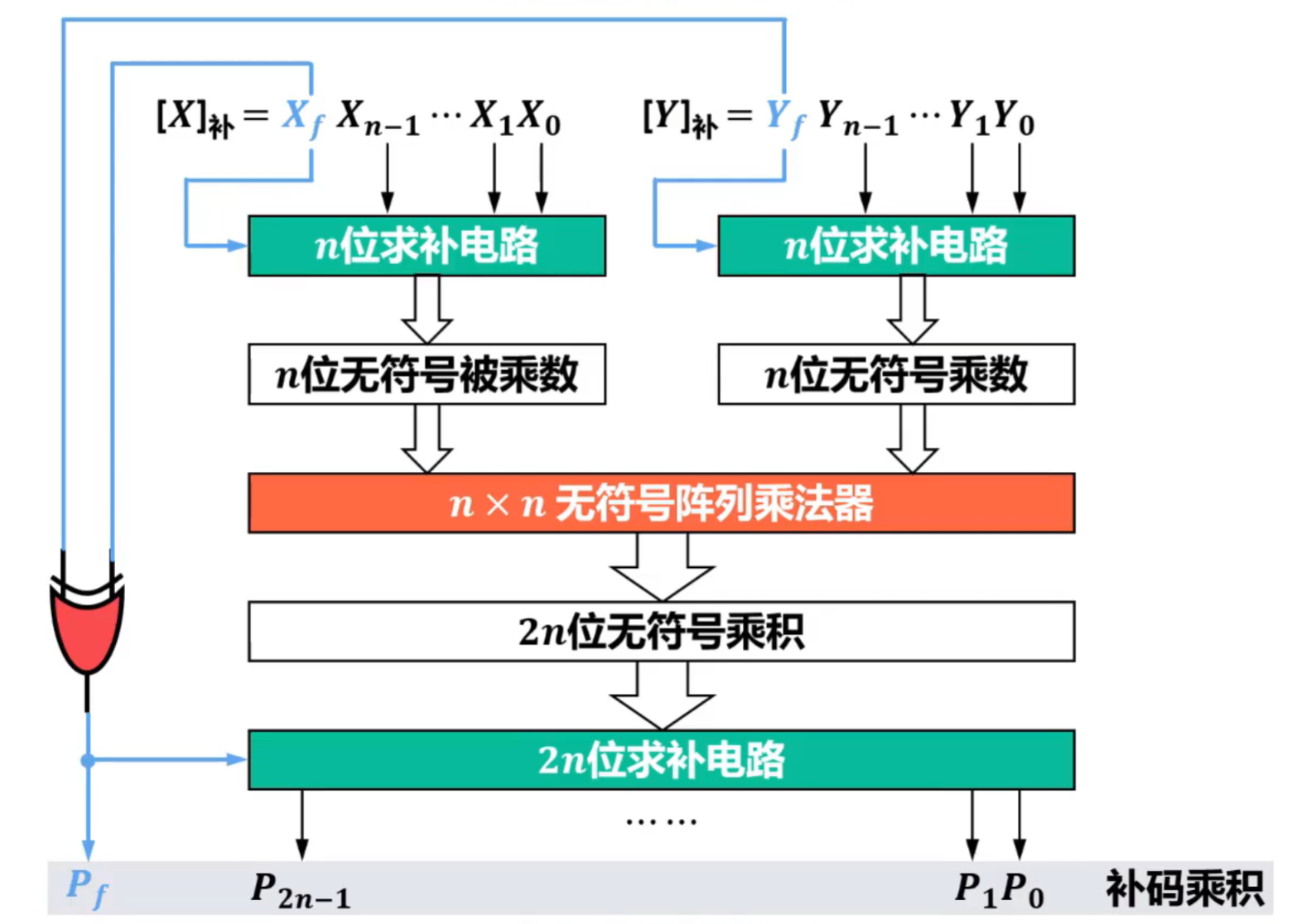
- 假设X为正数,Y为正数
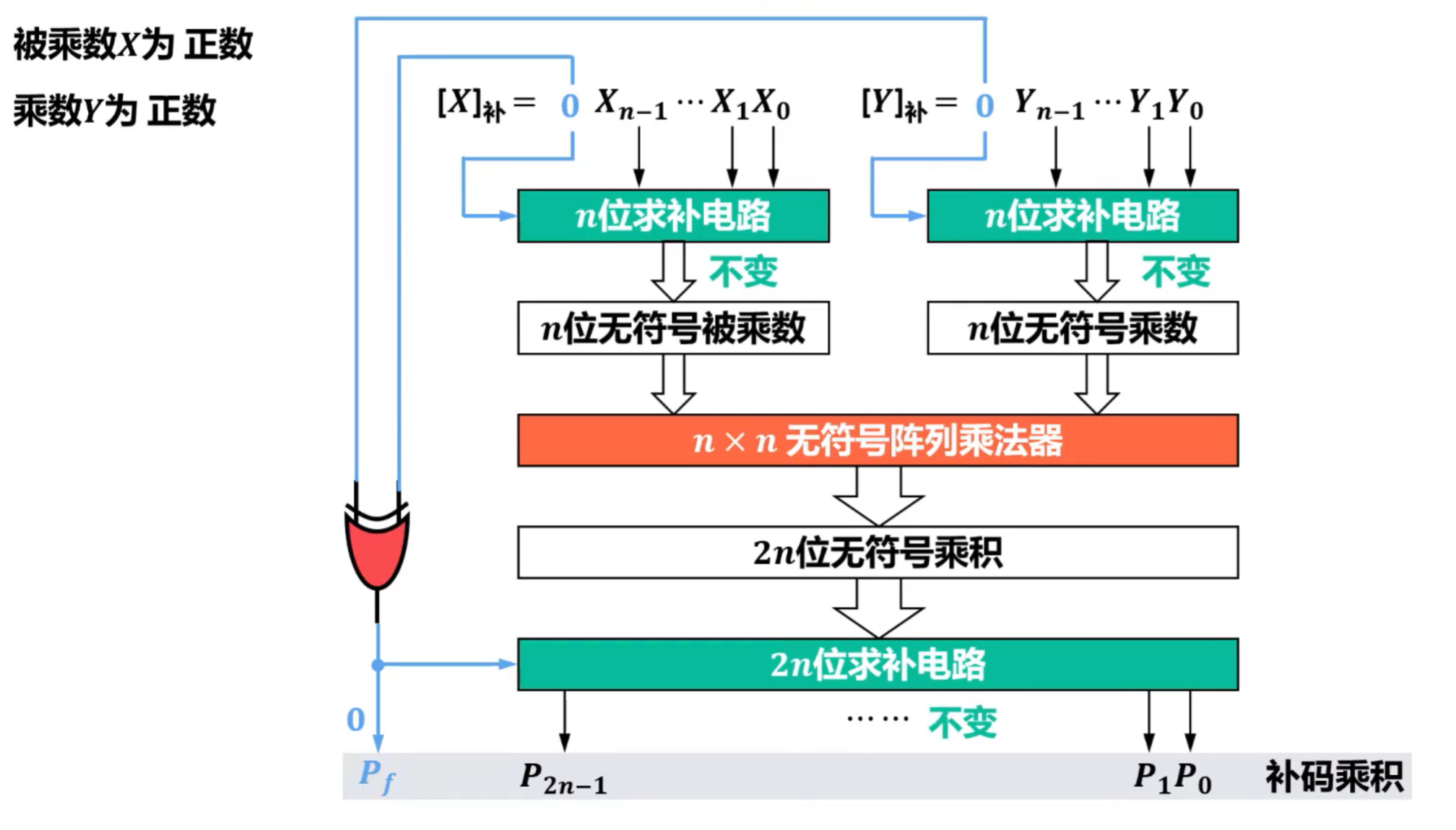
- 假设X为正数,Y为负数
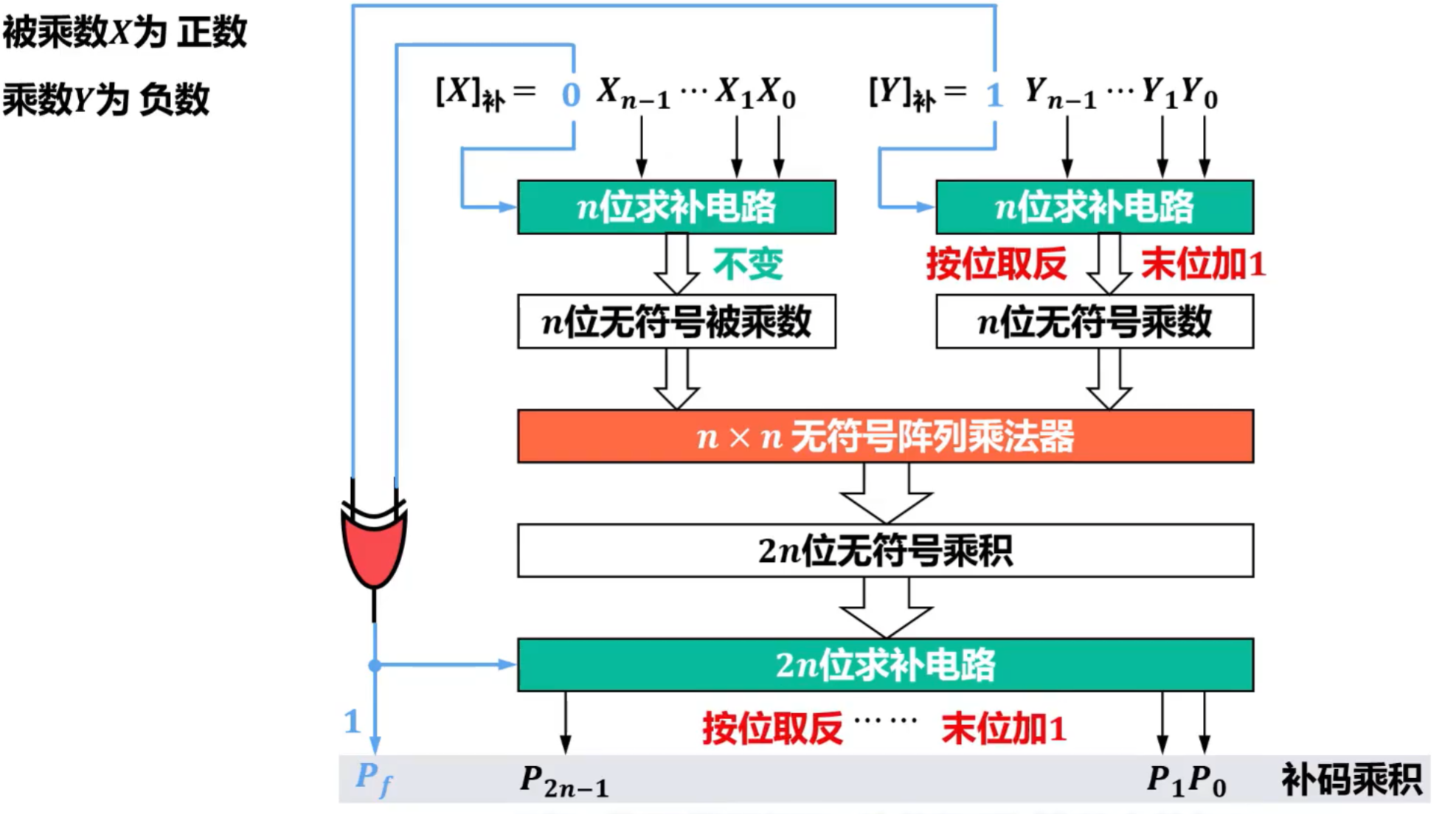
- 假设X为负数,Y为正数
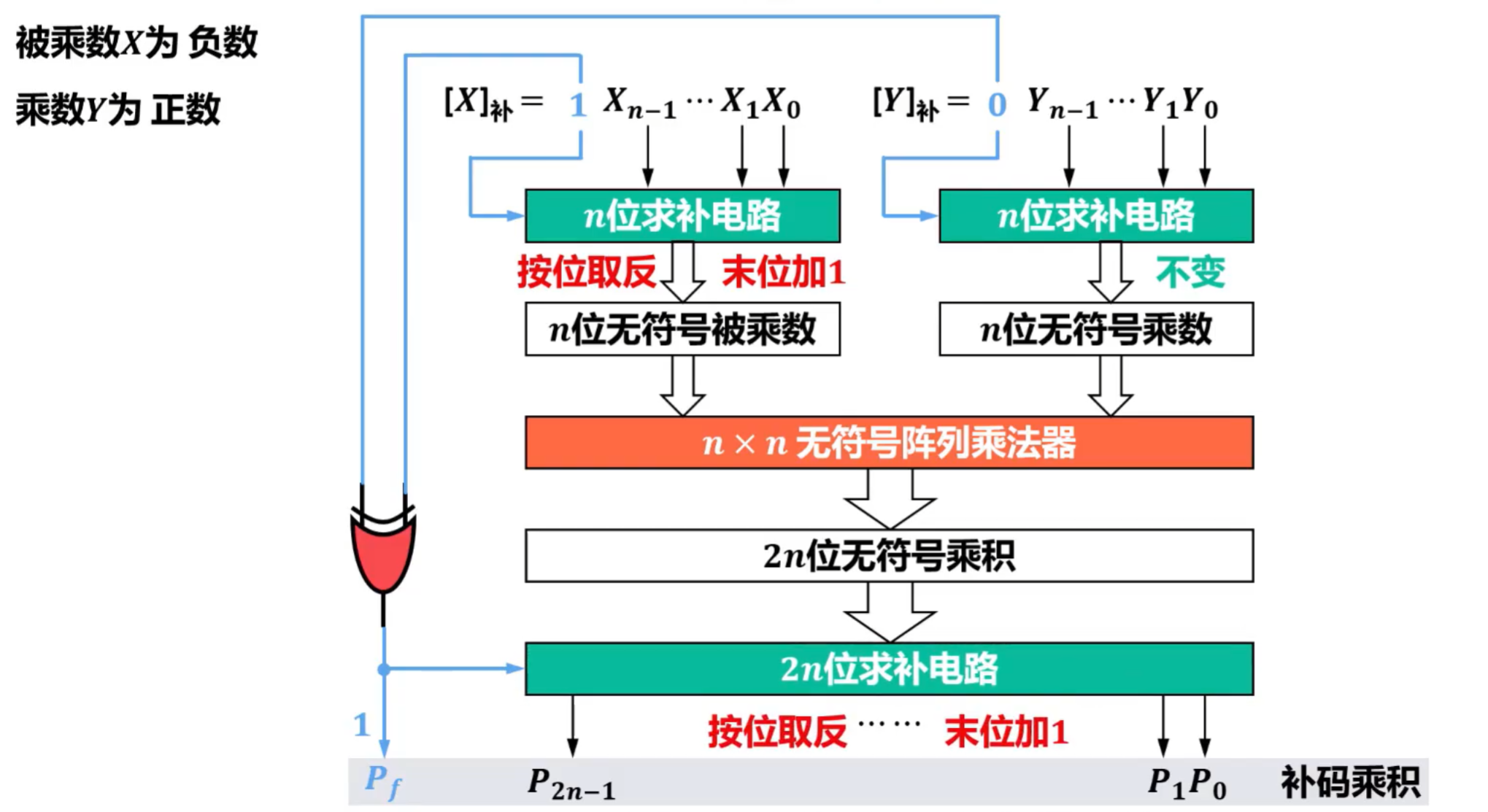
假设X为负数,Y为负数
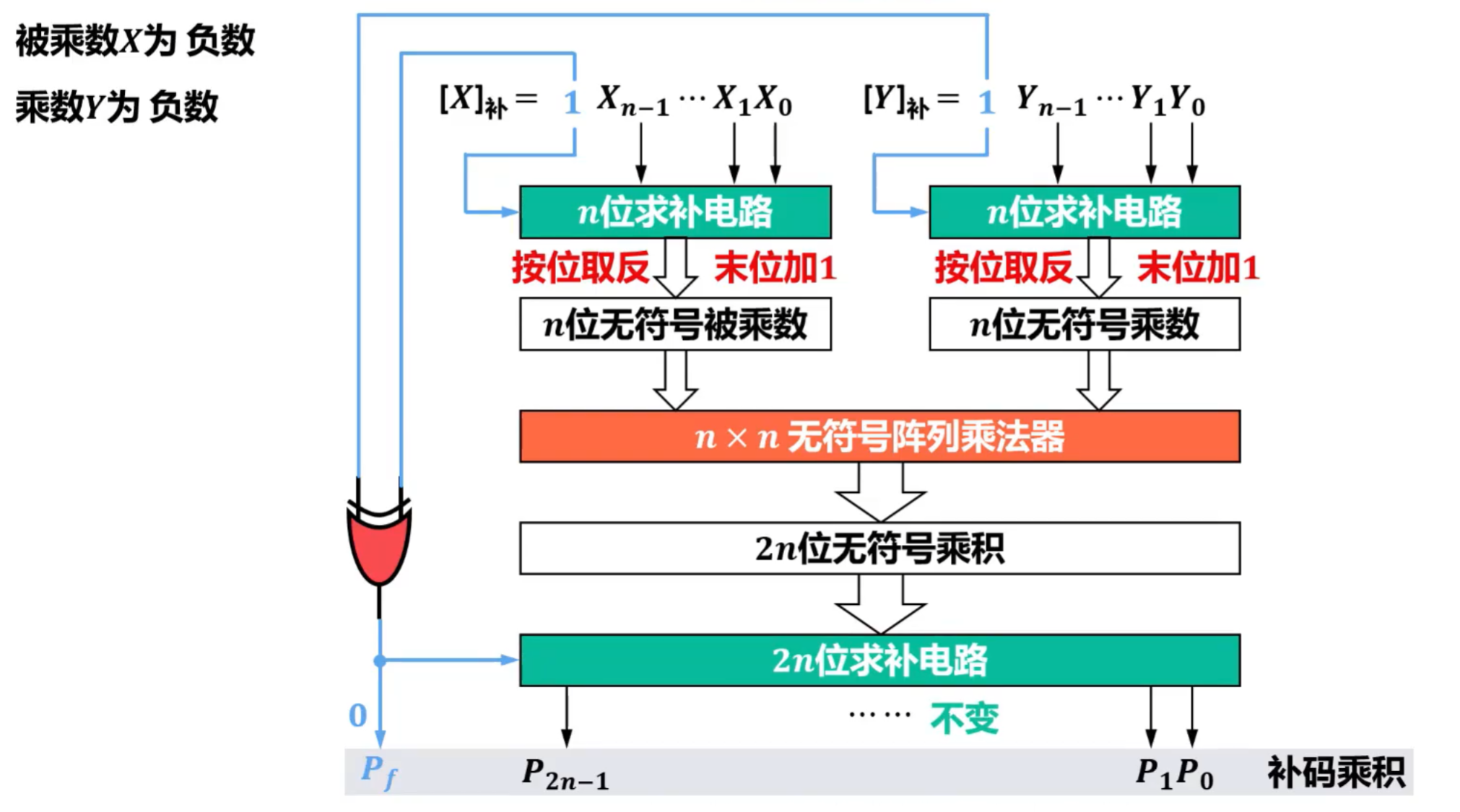
可以构建不使用求补电路,而使用补码直接参与乘法运算的直接补码乘法电路。
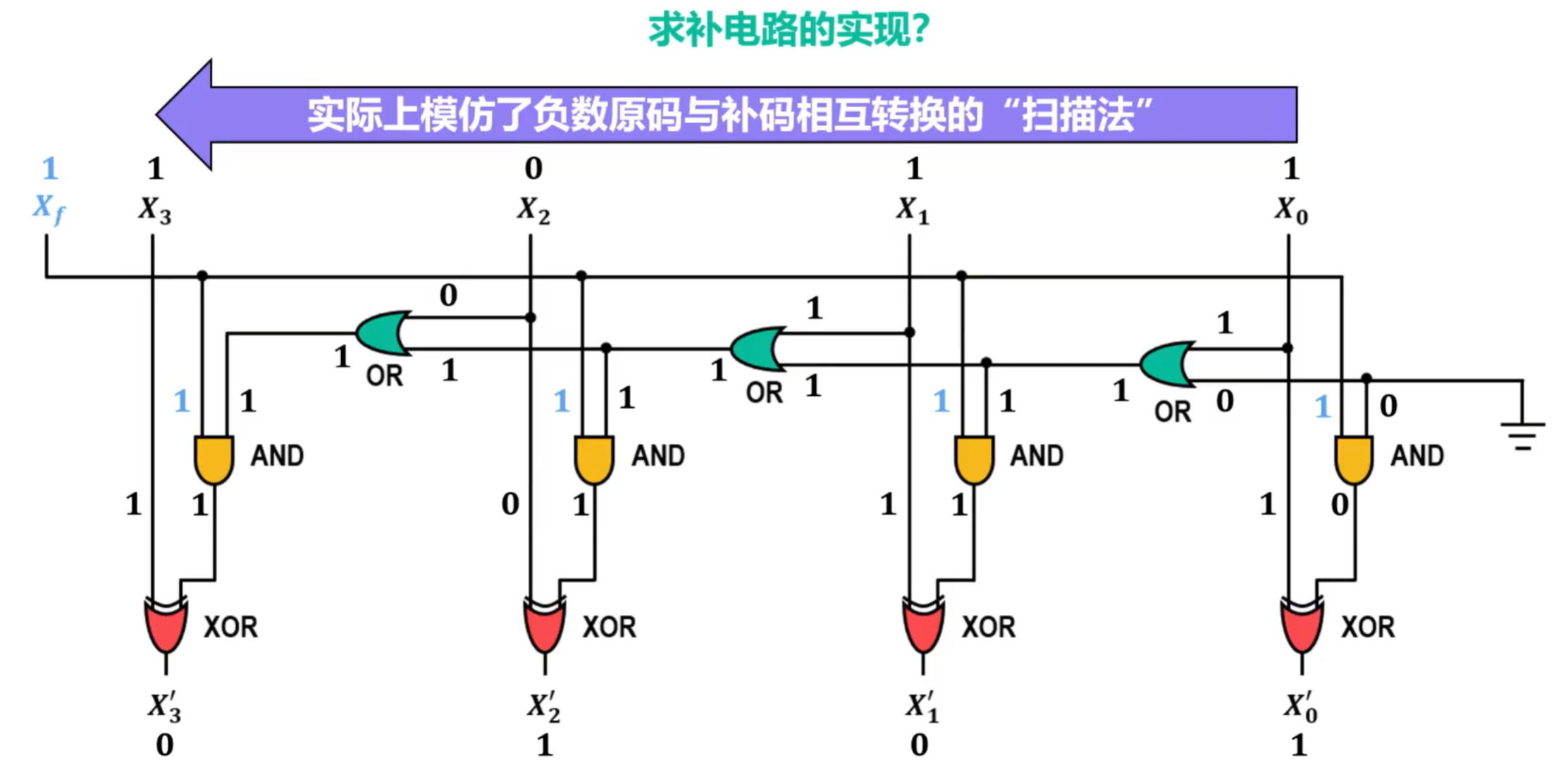
- 求补电路的实现
实际上,模仿了负数原码与补码相互转换的“ 扫描法 ”
6)原码除法运算(恢复余数法)
由于原码表示与无符号数非常类似,仅比无符号数多一个符号,因此,进行原码除法运算时,可将符号位与数值部分分开处理。
- 商的符号:由被除数和除数各自的符号进行异或运算求得;
- 商的数值部分:由被除数和除数各自的数值部分(即真值的绝对值)相除求得。

以上是定点小数(纯小数)原码除法运算的处理方法,为了确保商和余数也为定点小数(即不发生溢出),上述除法的条件为| X | < | Y |。同理,定点整数原码除法运算的条件为| X | ≥ | Y | 。
①原码除法的法则
- 前提条件:
- 除数 ≠ 0
- 定点小数:|被除数| < |除数|
- 定点整数:|被除数| ≥ |除数|
- 商的符号 = 被除数的符号 ⊕ 除数的符号
- | 商 | = | 被除数 | ÷ | 除数 |
- 将商的符号与**| 商 |**拼接在一起
②模拟二进制除法笔算过程

- 执行流程图
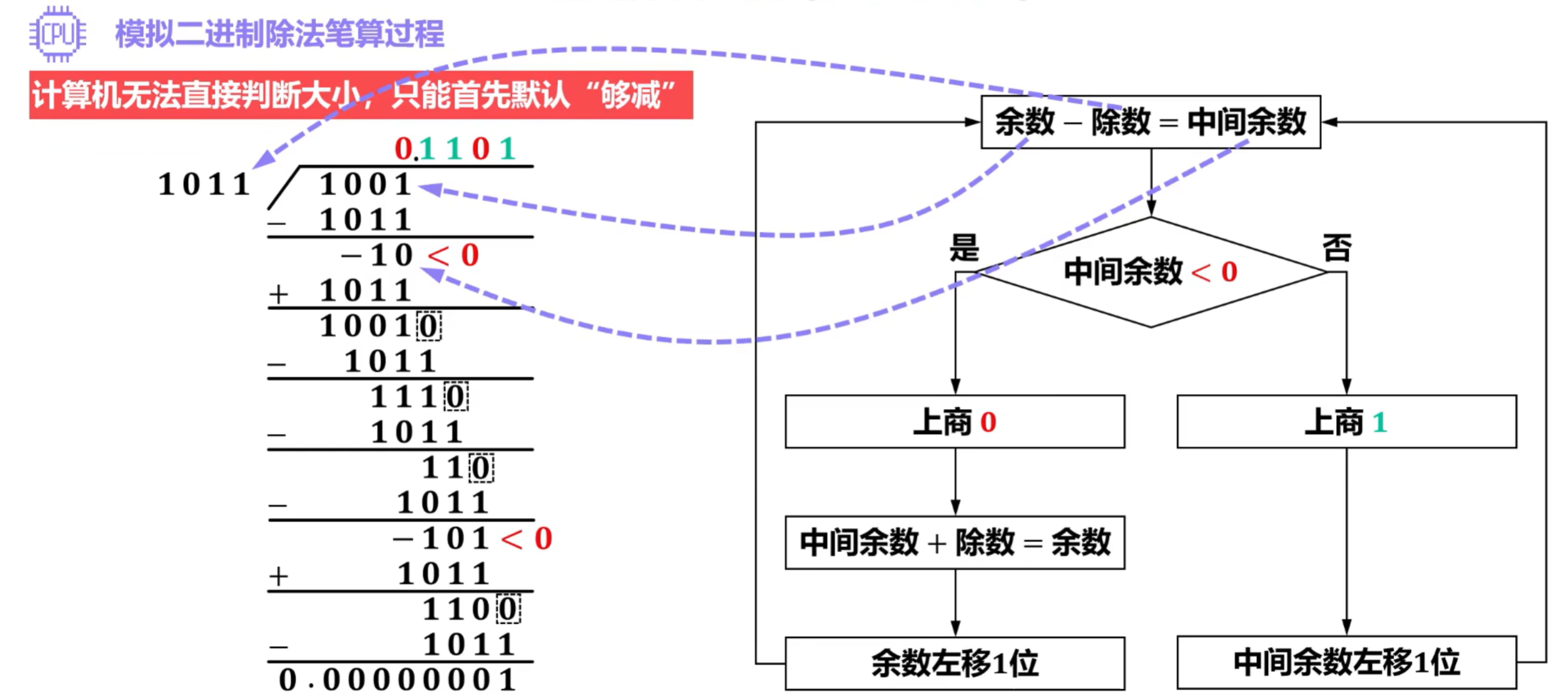
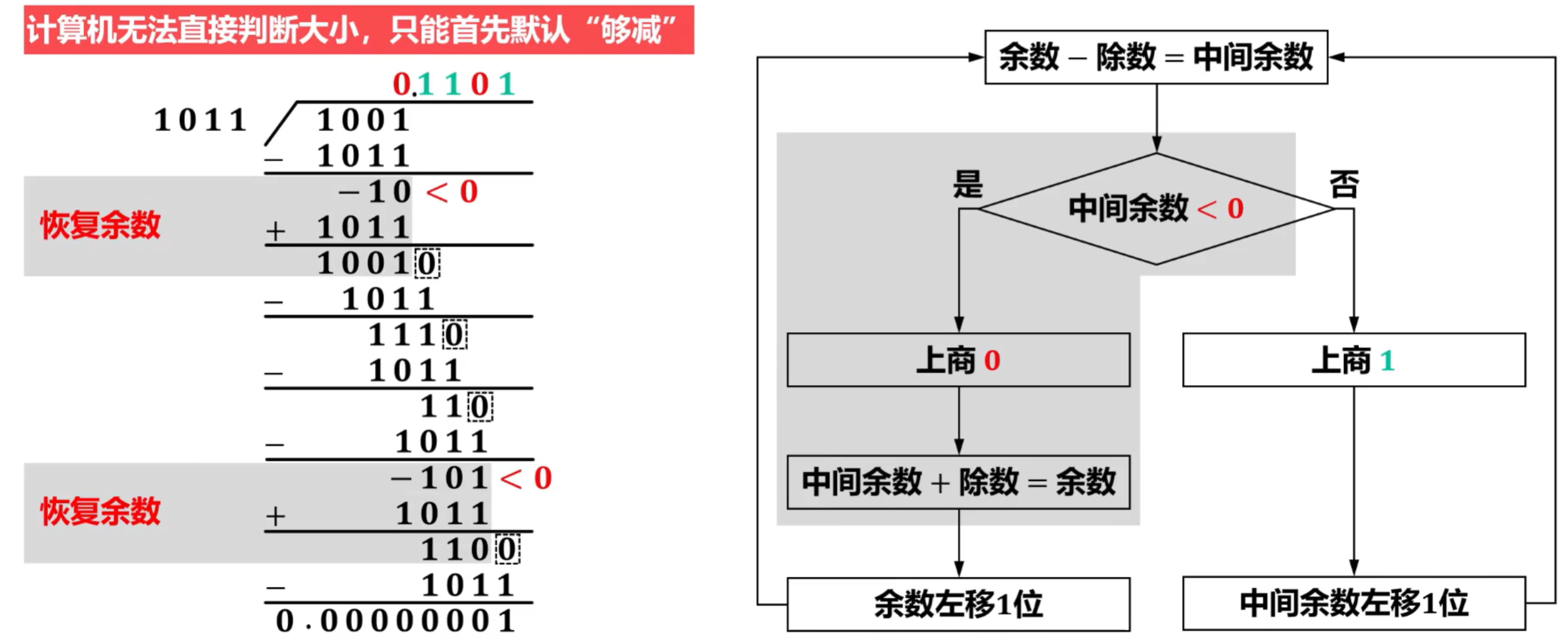
- 需要两次恢复余数,即加回除数
③硬件逻辑实现
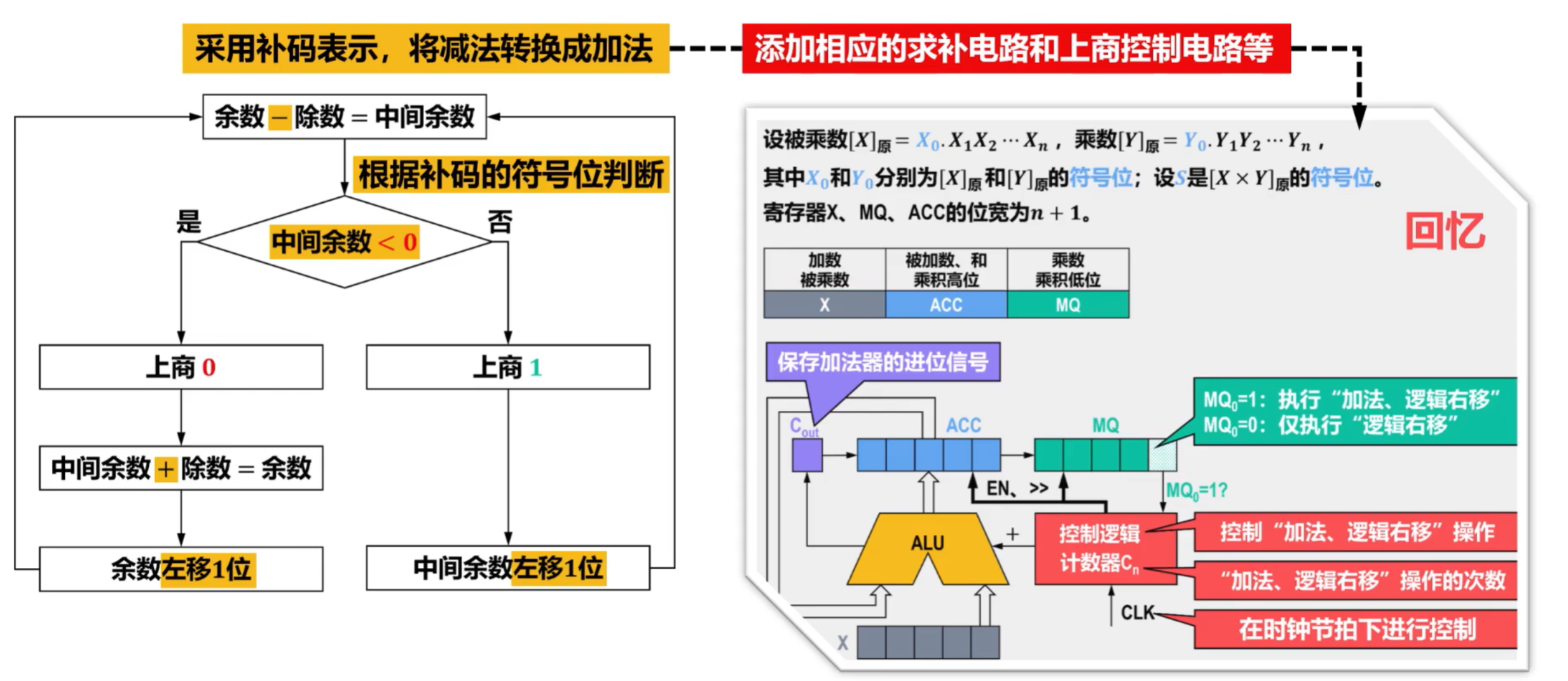
- 流程图各位置的解释
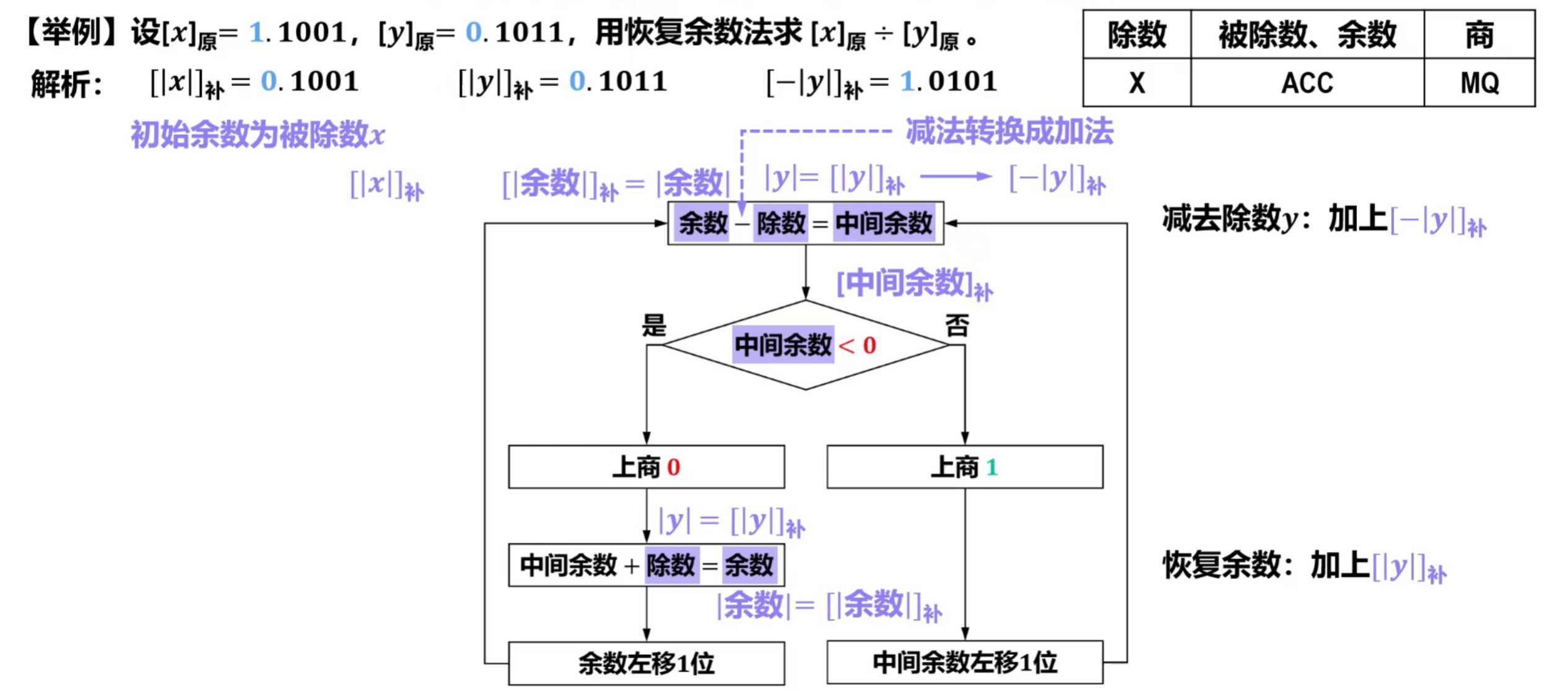
- 举例说明
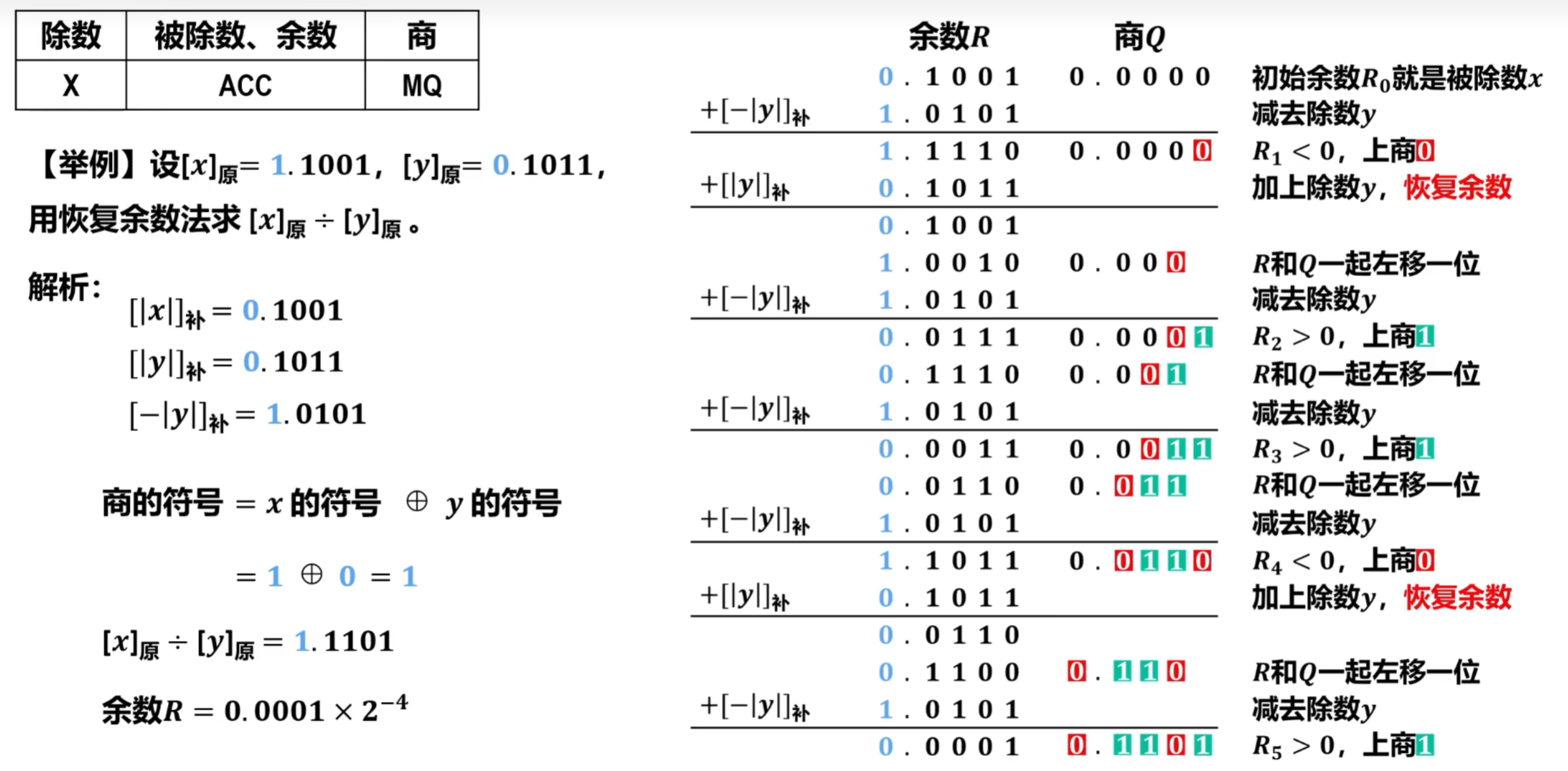
从本例可以看出,由于运算过程中可能需要恢复余数,并且恢复余数的次数和具体的操作数相关,极端情况下每一步运算都需要恢复余数,因此,该方法的最大缺点是运算时间不确定,另外,其控制电路也比较复杂。
例题:

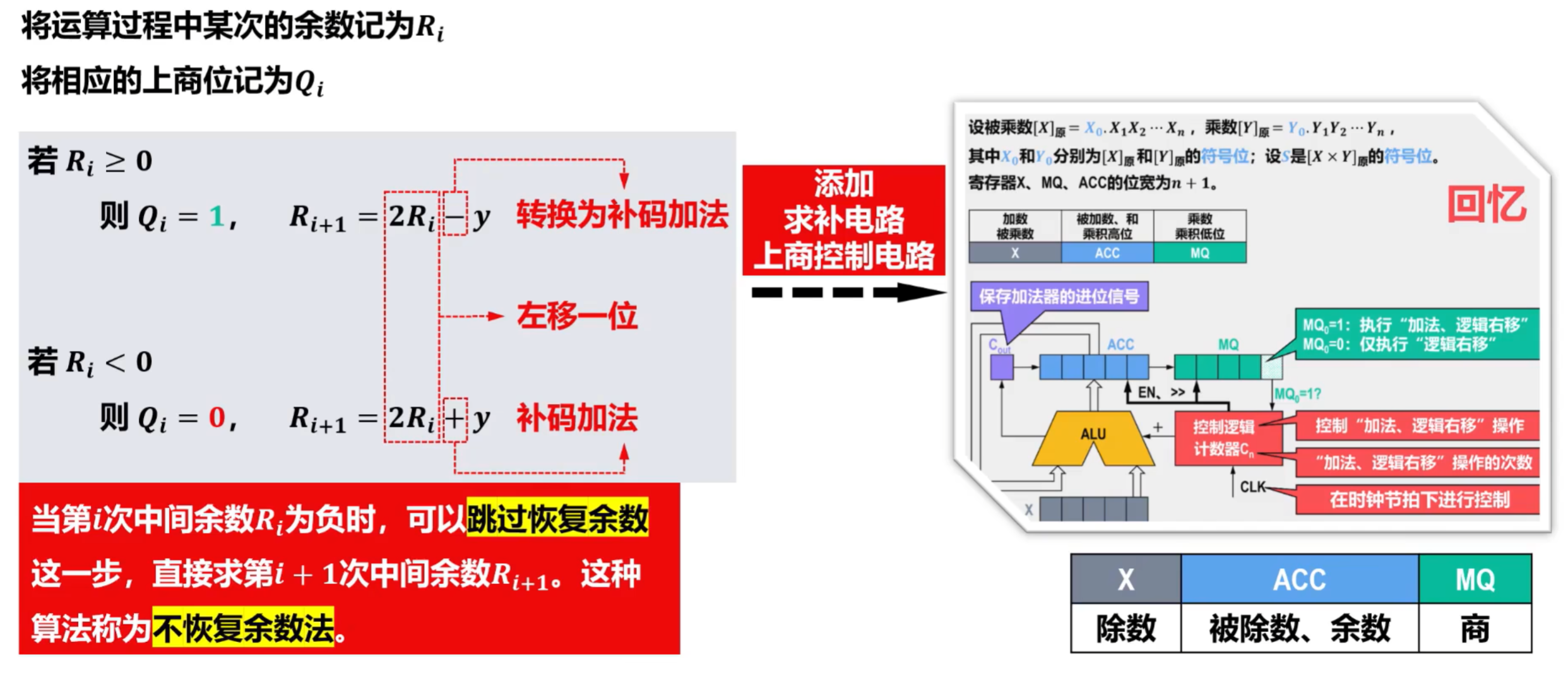
7)原码除法运算(不恢复余数法)
不恢复余数法实际上是对恢复余数法的改进,不恢复余数法又称为加减交替法。
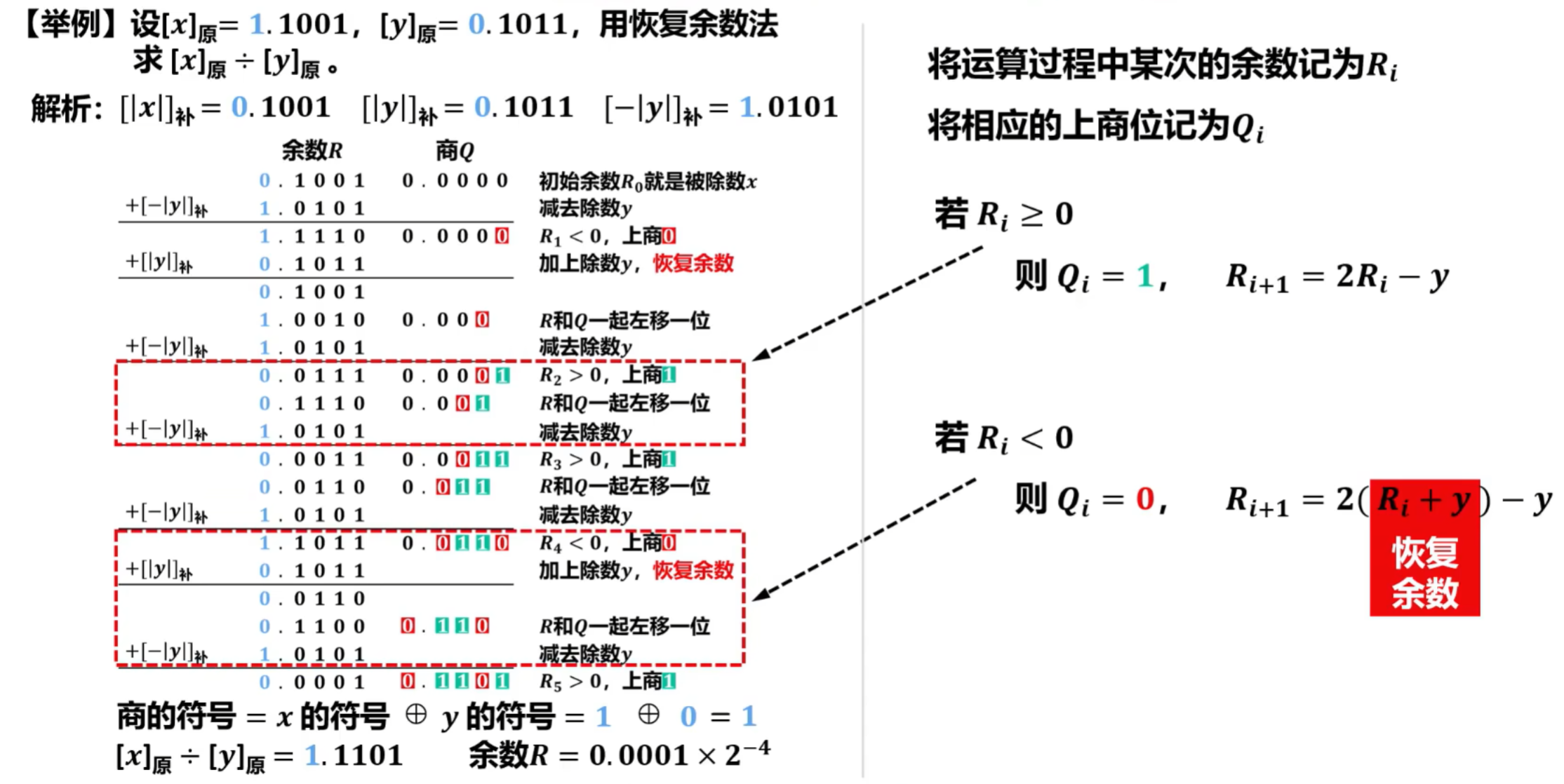
- Ri是计算后的符号位,见上图可知。根据余数Ri的符号,决定加还是减除数y的运算,又称为加减交替法。
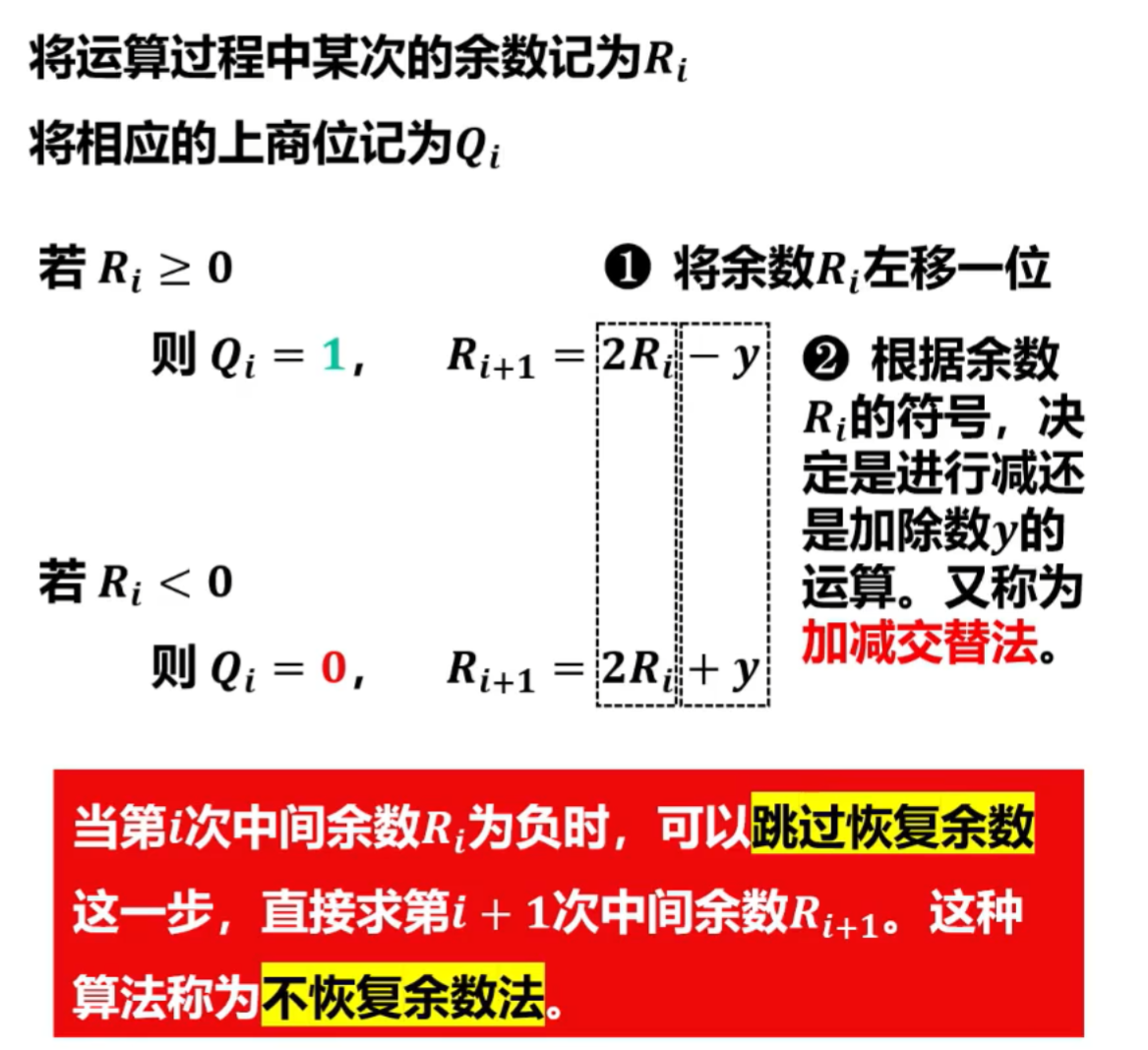
①不恢复余数法的演示过程
- 求得余数R和商Q
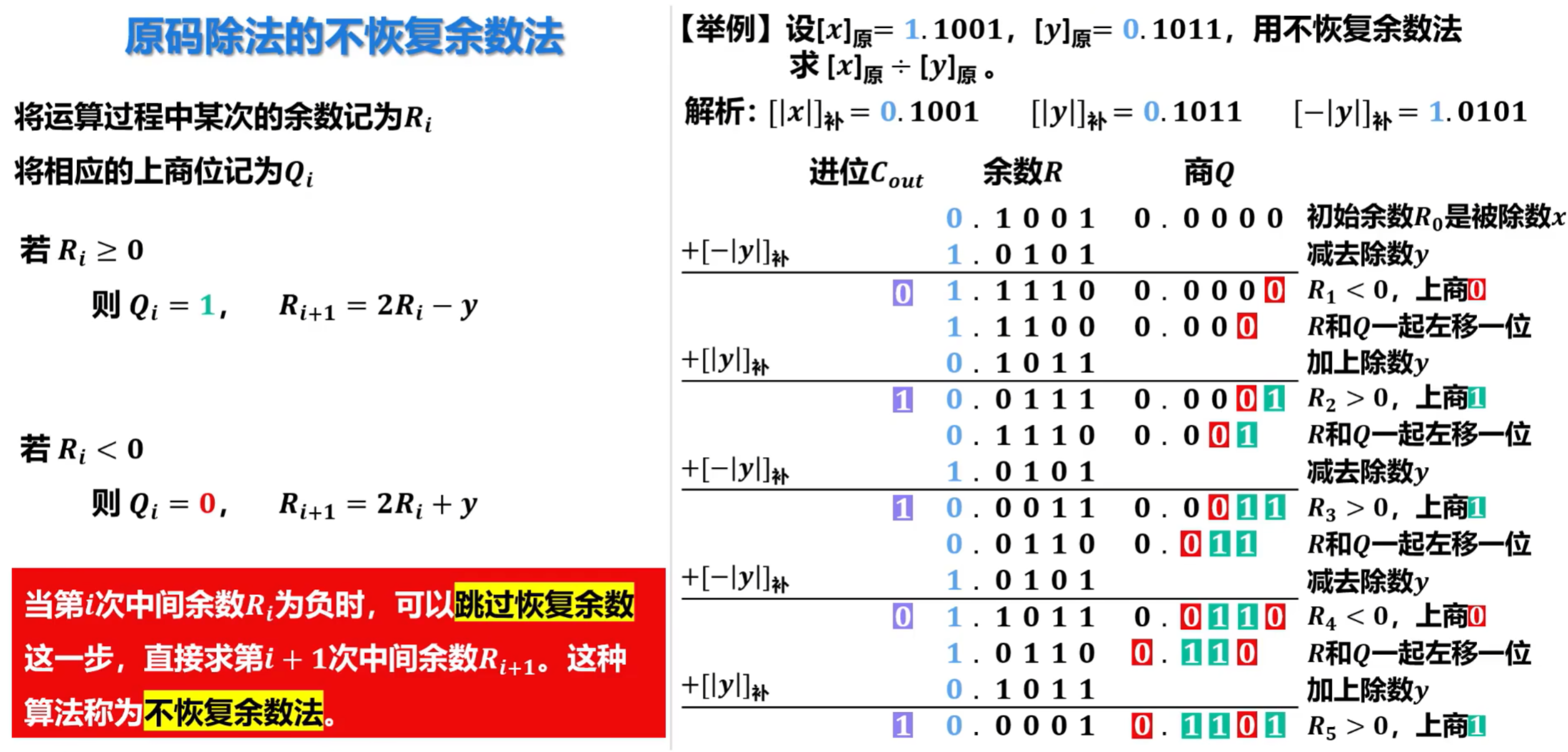
- 求得商的符号

例题:

②硬件逻辑实现
与乘法器相比,需要添加求补电路,乘法器中执行加法、逻辑右移,除法运算则是左移1位。
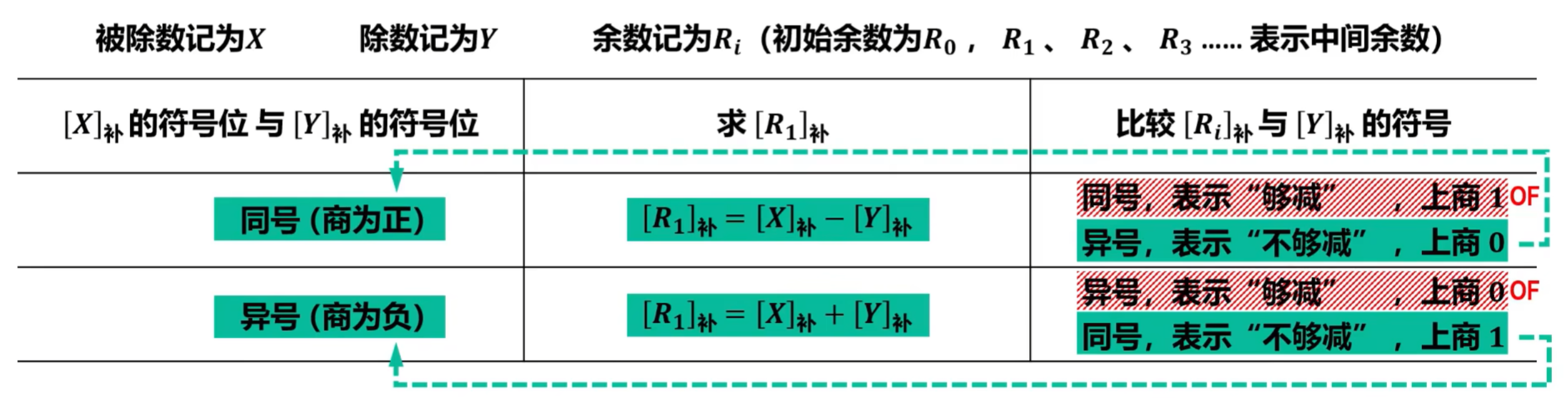
8)补码除法运算(不恢复余数法)
与原码除法将符号位和数值部分分开处理不同,补码除法将符号位和数值部分一起参加运算,商符是在求商的过程中自然形成的。因此,补码除法的运算方法没有原码除法的运算方法直观,需要解决以下3个主要问题:
- 如何确定商值
- 如何形成商符
- 如何得到新余数
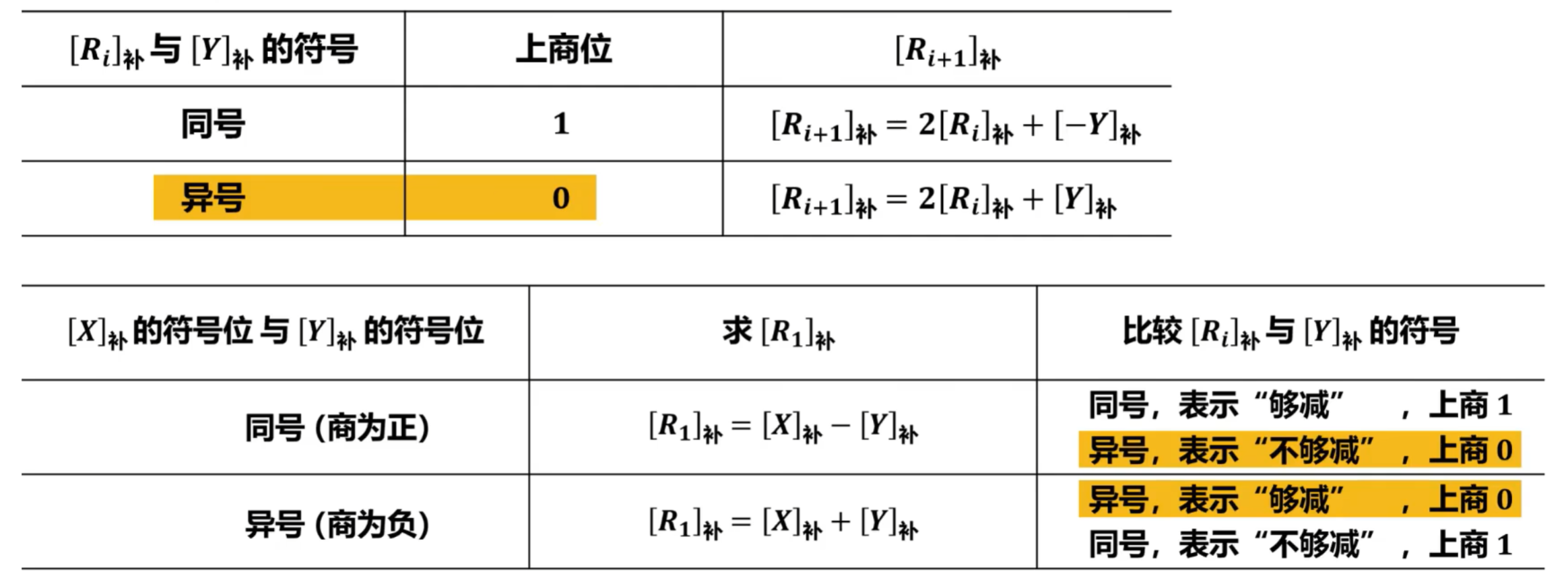
①确定商值
-
由于补码除法中的被除数、除数和中间余数都是有符号的,因此,不能像原码除法(符号位单独处理)那样直接用做减法来判断是否“ 够减 ”。
-
补码除法判断是否“ 够减 ”的依据是:中间余数(初始为被除数)与除数之间符号的异同以及相应做减法或加法后结果的符号。


-
在判断出是否“ 够减 ”后,就可以确定相应的上商位的值:
-
若 [X]补 与 [Y]补 同号,则商为正,“ 够减 ”时上商 1,“ 不够减 ”时上商0(按原码规则上商);
-
若 [X]补 与 [Y]补 异号,则商为负,“ 够减 ”时上商 0,“ 不够减 ”时上商1(按反码规则上商);

-
②形成商符
-
补码除法将符号位和数值部分一起参加运算,商符是在求商的过程中自然形成的
- 在定点小数(纯小数)的除法中,被除数的绝对值必须小于除数的绝对值,否则商会大于1而溢出。
③得到余数
-
新余数 [Ri+1]补 的获取方法与原码除法不恢复余数法(加减交替法)是类似的,规则如下:
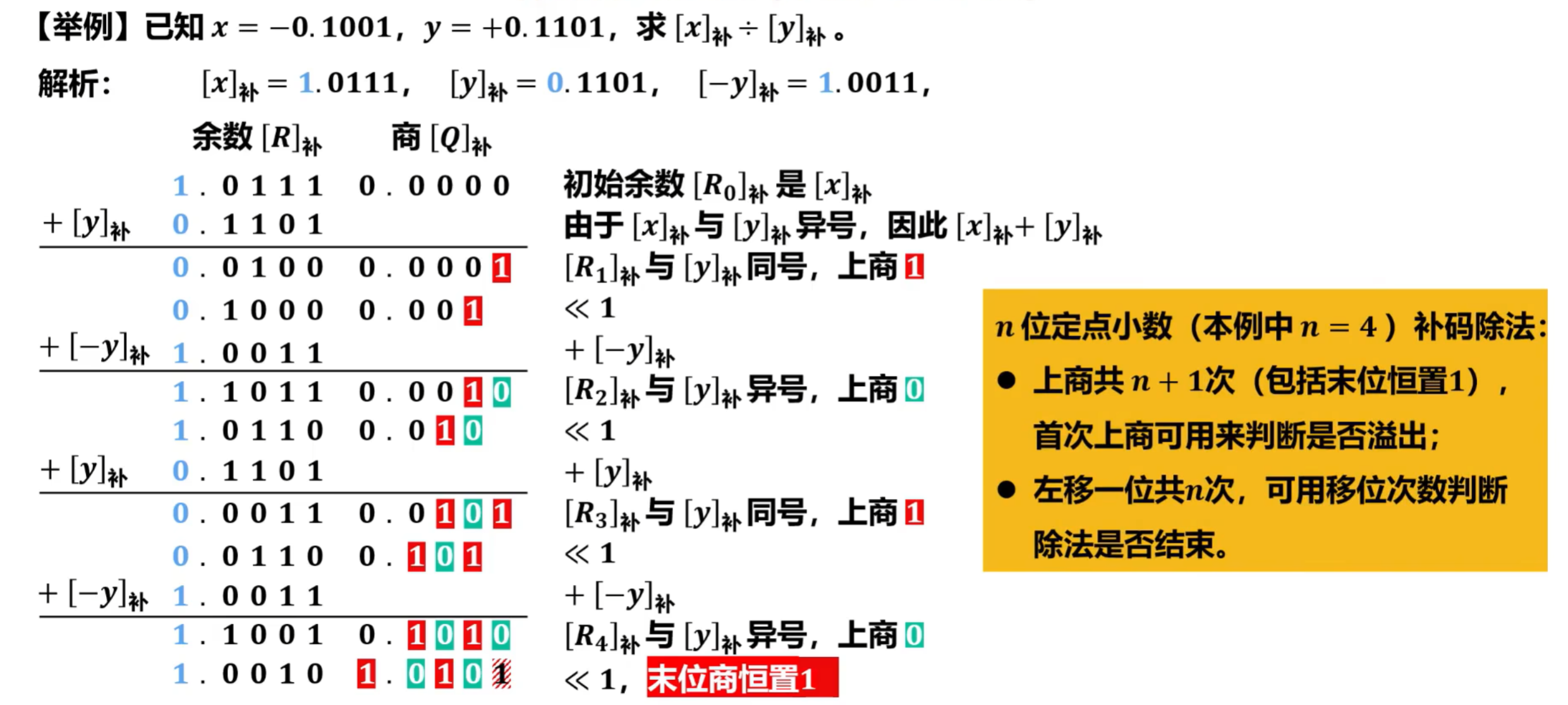
④补码除法的计算过程
将上述的步骤总结如下:

如果对商的精度没有特殊要求,一般可采用“ 末位恒置 1 ” 法,这种方法操作简单,易于实现,而且最大误差仅为2-n 。
例题:

4、浮点数运算
1)浮点加减法运算
①引入

- 在尾数右规时,尾数未位的几位会因超出计算机字长而被丢弃,从而产生误差。此时,计算机可以按选定的方式进行舍入操作
- 在尾数规格化和尾数舍入时,可能会对结果的阶码执行加、减运算。因此,必须考虑结果的阶码出现溢出的问题
- 由于浮点数中阶码的位数决定了浮点数的表示范围,因此,对于浮点运算,当阶码出现溢出时,表示运算结果出现溢出。
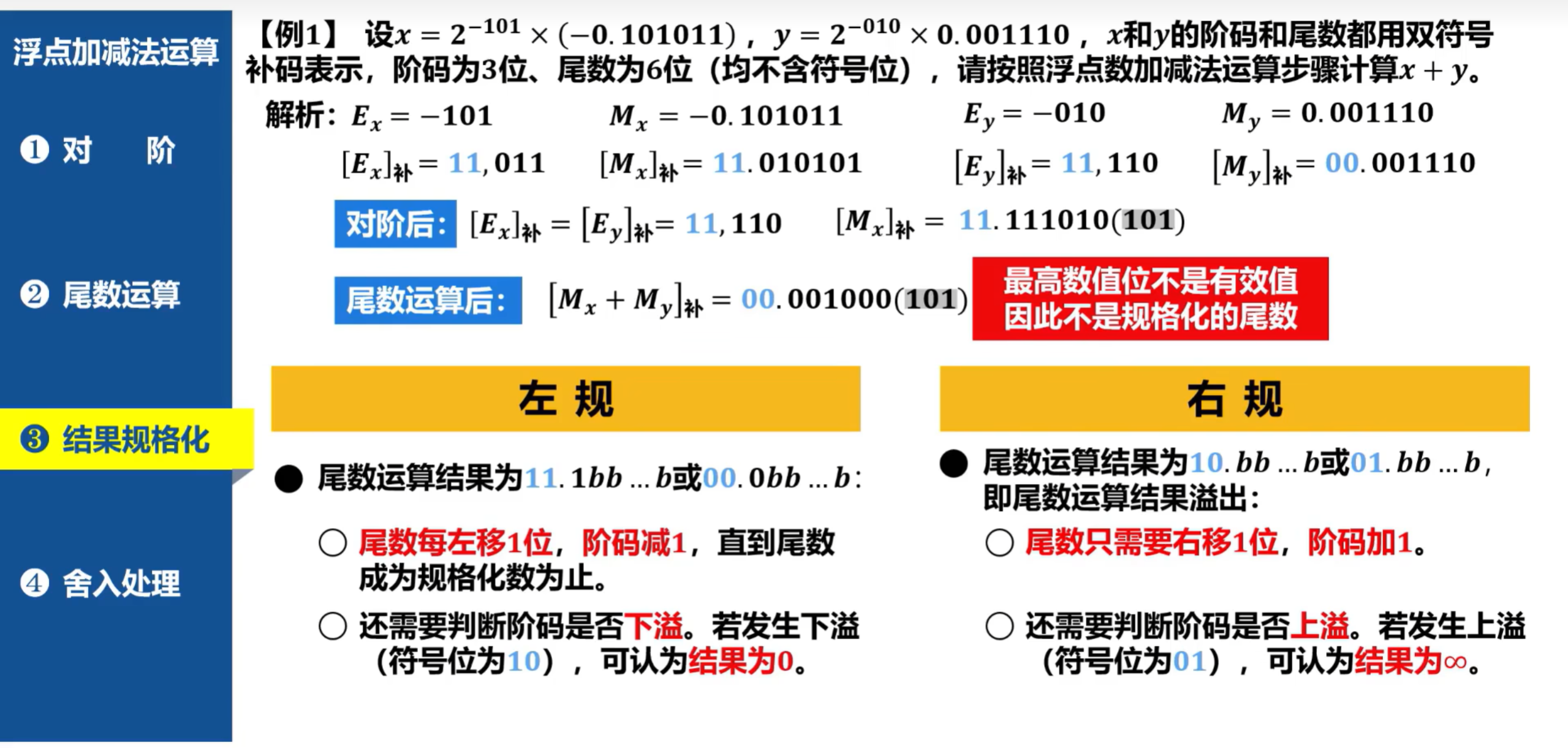
②浮点加减法运算步骤
- 对阶
- 对阶原则:小阶向大阶看齐,尾数右移相应位数(两个阶的差的绝对值)

- 尾数运算
- 将x和y的补码尾数进行相加,记作 [Mx + My]补

-
结果规格化
-
将得到的尾数运算结果进行结果规格化(注:并不是每个结果都需要规格化,如果溢出则不需要,表示为溢出错误)
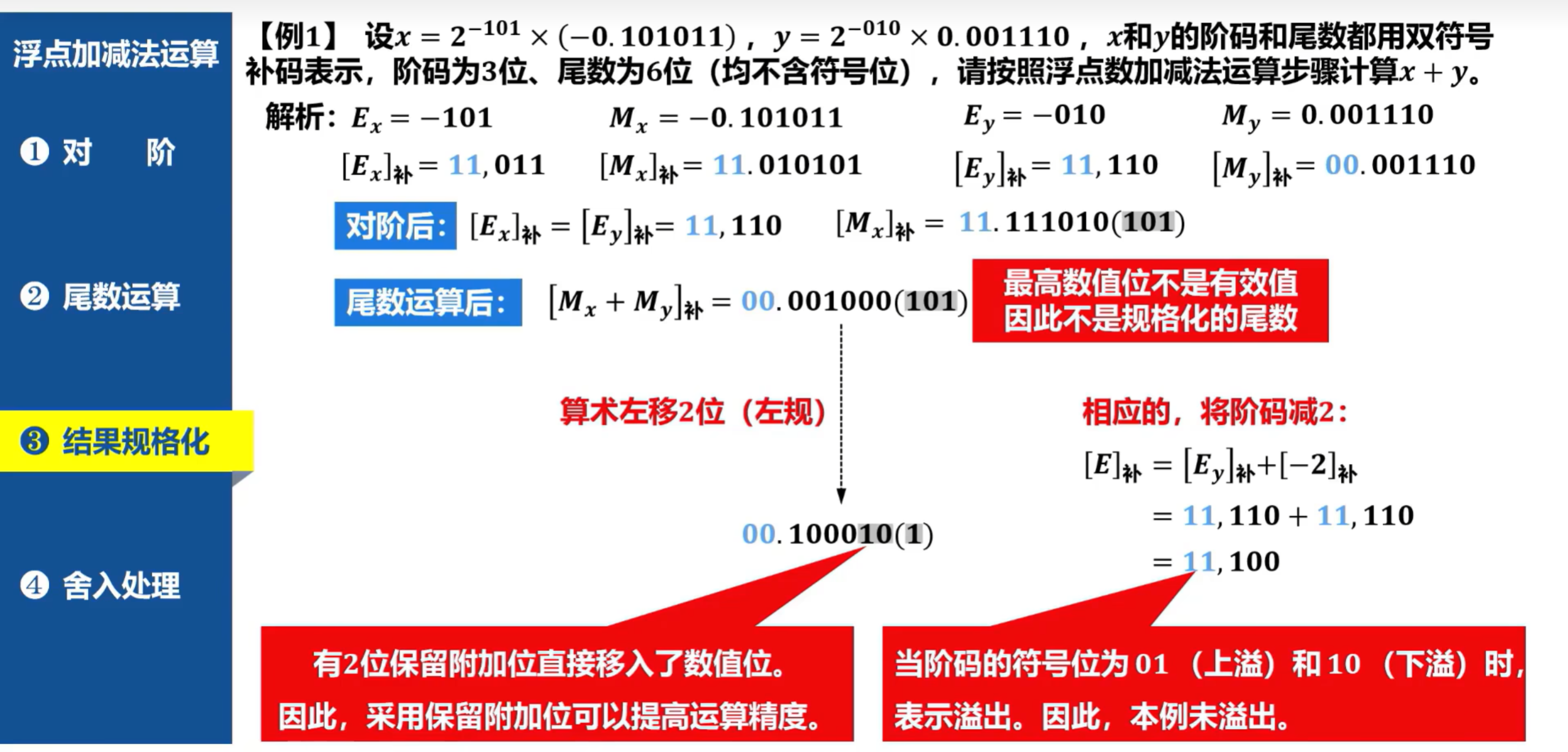
- 此处需要进行算术左移2位,即左规2位
- 舍入处理
- 对于舍入处理,又三种处理方式,分别是截断法、末尾恒置1法和0舍1入法

- 使用三种不同的方法得到以下结果

采用0舍1入的舍入操作,若破坏规格化结果,则还需要再次进行规格化处理。
- 得到最终结果

例题:

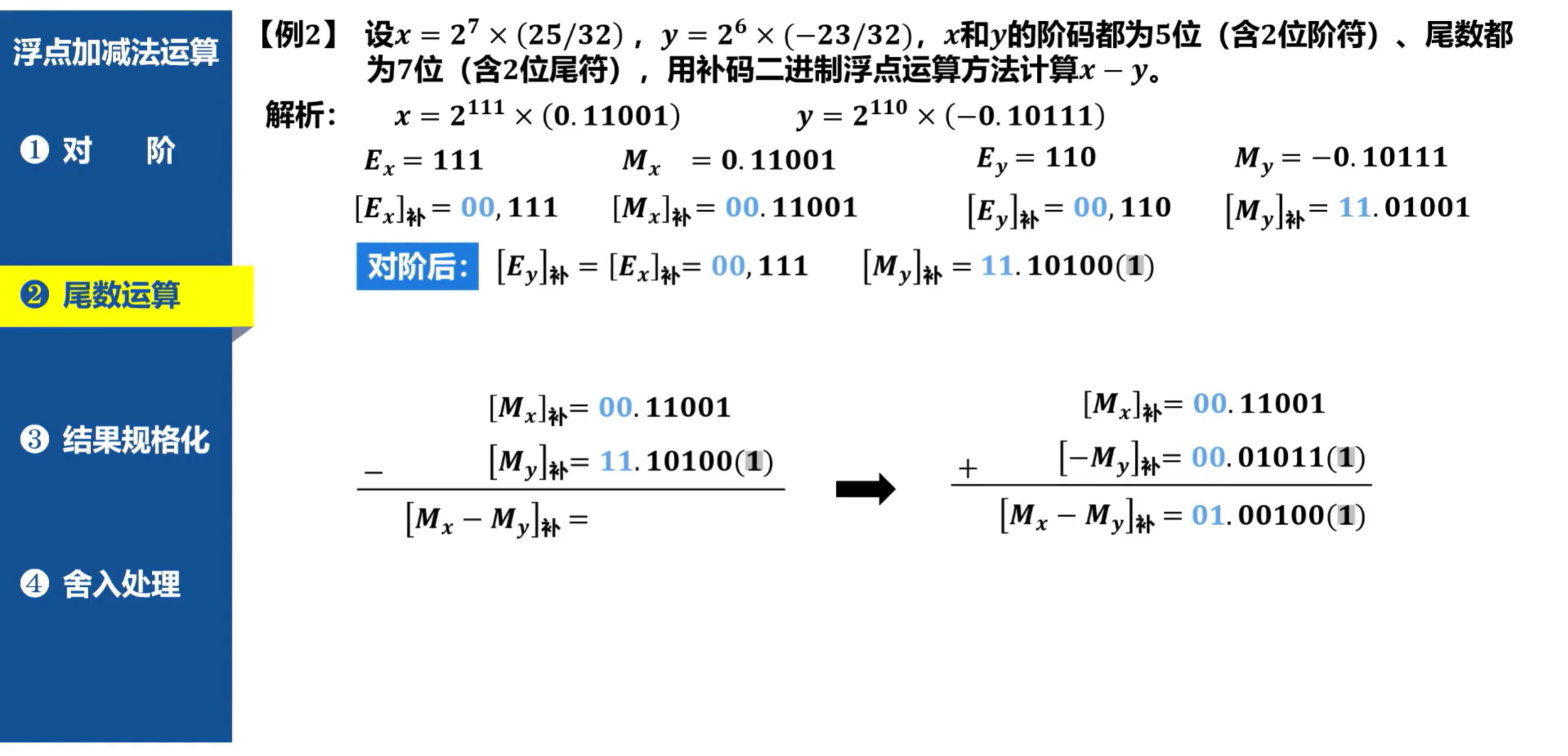
- 此处的尾数运算结果溢出,则不需要进行结果规格化,判定上溢,运算结束,结果为∞


③本节总结

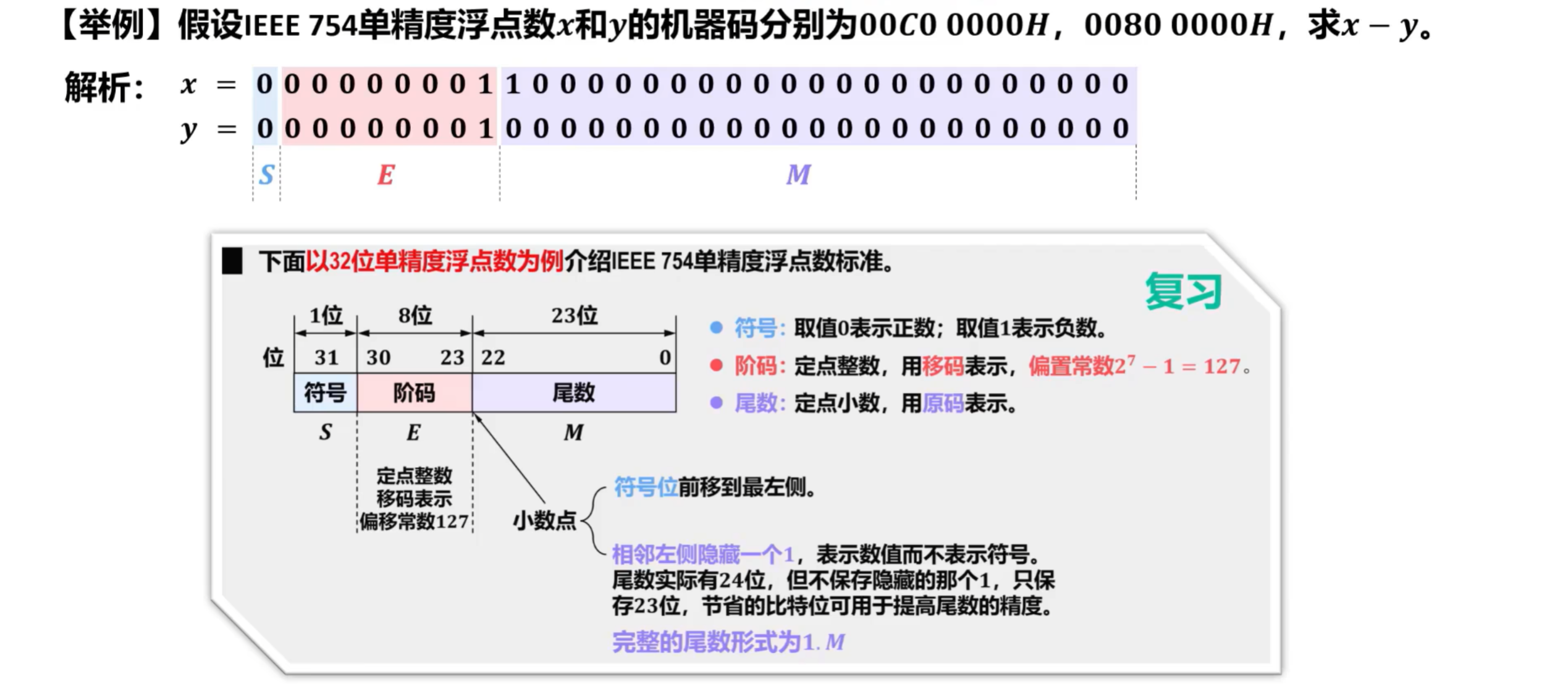
2)IEEE 754 浮点加减法运算
①运算方式
- IEEE 754 浮点数的阶码采用移码表示,尾数采用原码表示,并且尾数的最高位隐藏
- IEEE 754浮点数的加减运算与上一节的基于补码表示的浮点数的加减运算有如下不同:
- 在对阶和结果规格化过程中,涉及到阶码的加减运算时采用移码的加减运算规则
- 尾数运算采用原码运算规则,且隐藏位要参与尾数运算
- 隐藏位参与尾数规格化判断和规格化过程:
- 若尾数形式为1.xxx,则为规格化尾数;
- 若尾数形式为0.xxx,则需要进行左规(将尾数左移1位,相应地将阶码减1),直到尾数规格化为止;
- 若尾数形式为1b.xxx,则需要进行1次右规(将尾数右移1位,相应地将阶码加1)。
- 舍入处理:
- 就近舍入:舍入为可表示的最近的数,如果数据正好处于两个可表示的数的中间,则向偶数舍入;
- 朝正∞方向舍入:总是取右侧可表示的最近的数;
- 朝负∞方向舍入:总是取左侧可表示的最近的数;
- 截断处理:直接丢弃多余位,朝0方向舍入。
- 溢出判断:
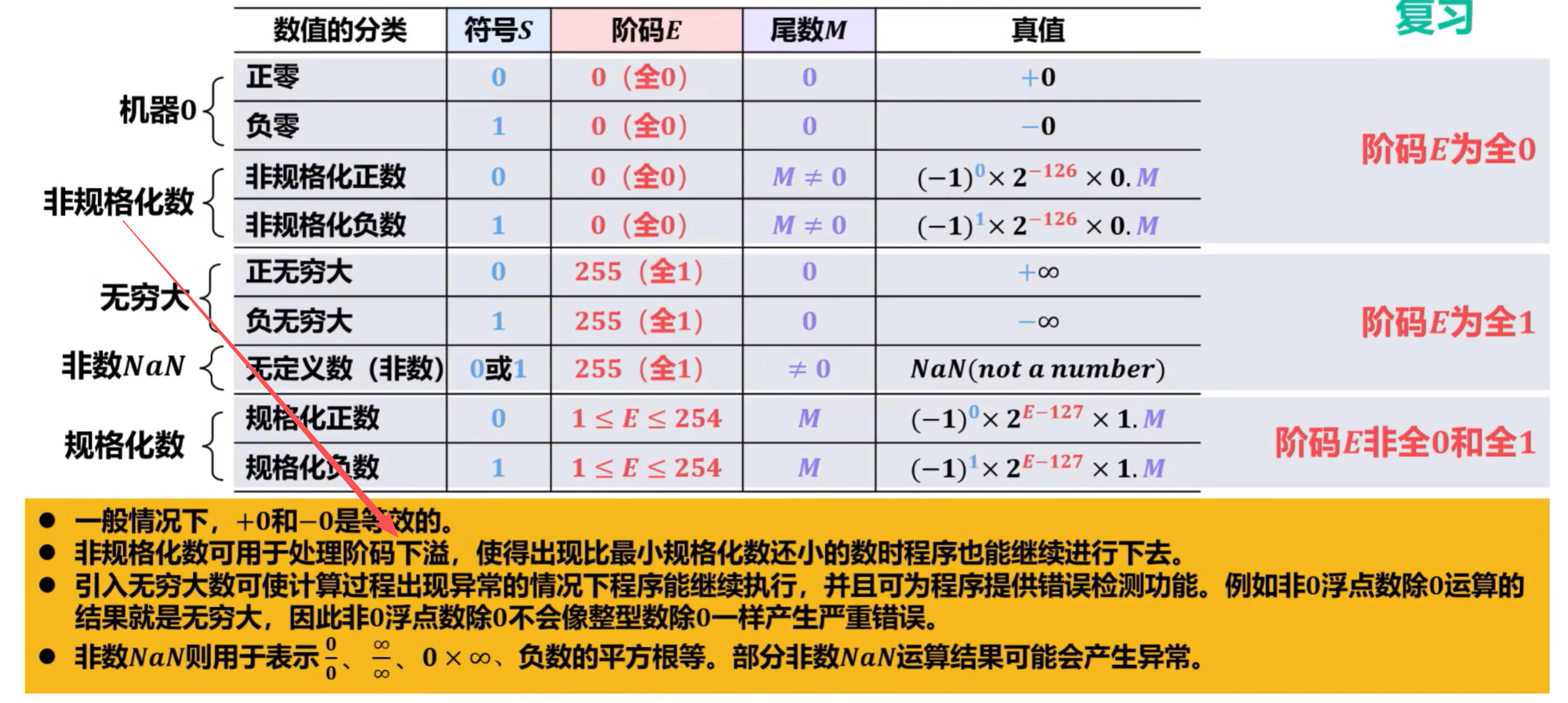
- 浮点运算的溢出可通过阶码的溢出来判断。对于IEEE 754单精度浮点数而言,向右规格化使阶码为全1(即11111111,真值为-128)时发生规格化上溢;向左规格化使阶码为全0时发生规格化下溢。
②运算过程
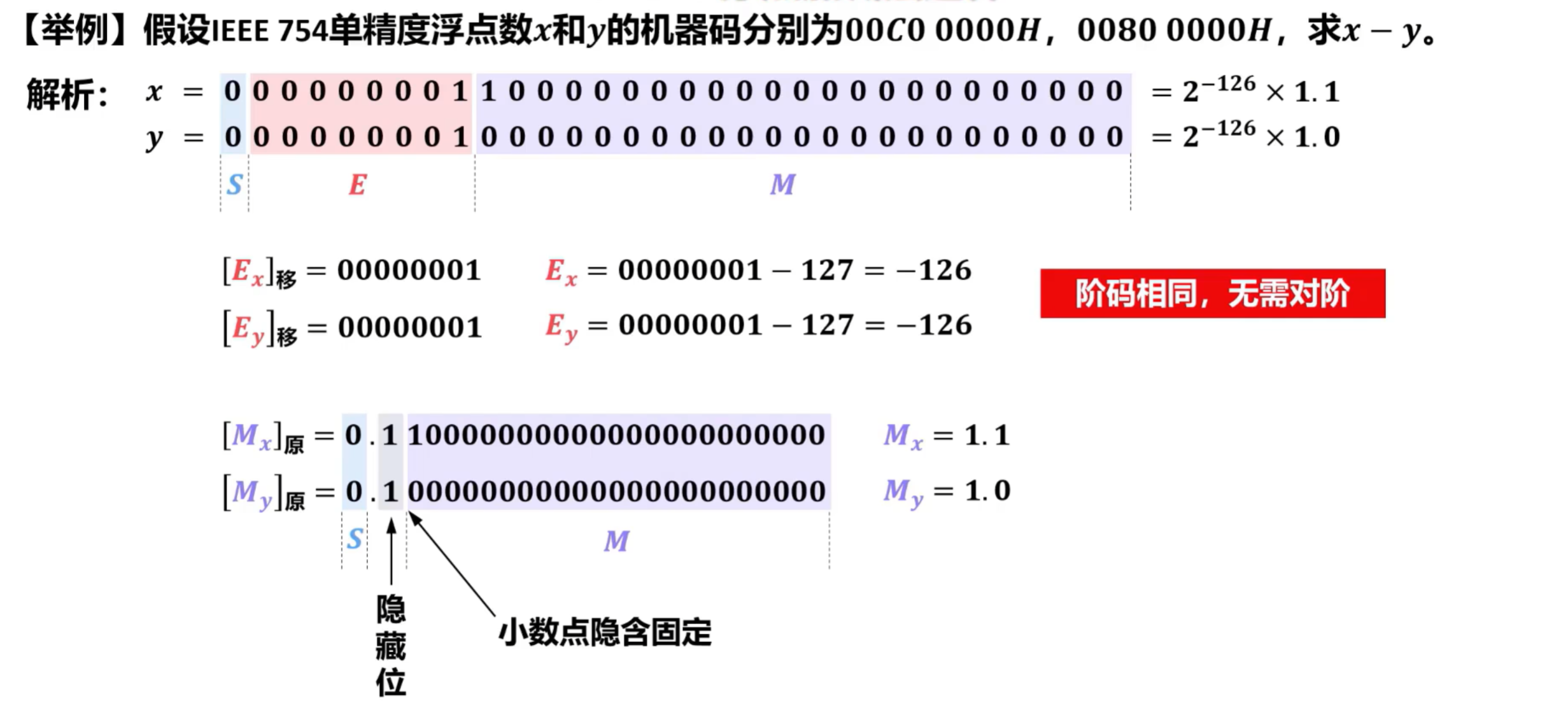

- 此处的规格化下溢,查看IEEE 754浮点数的取值范围,如下:
- 处理如下:

3)浮点乘法运算
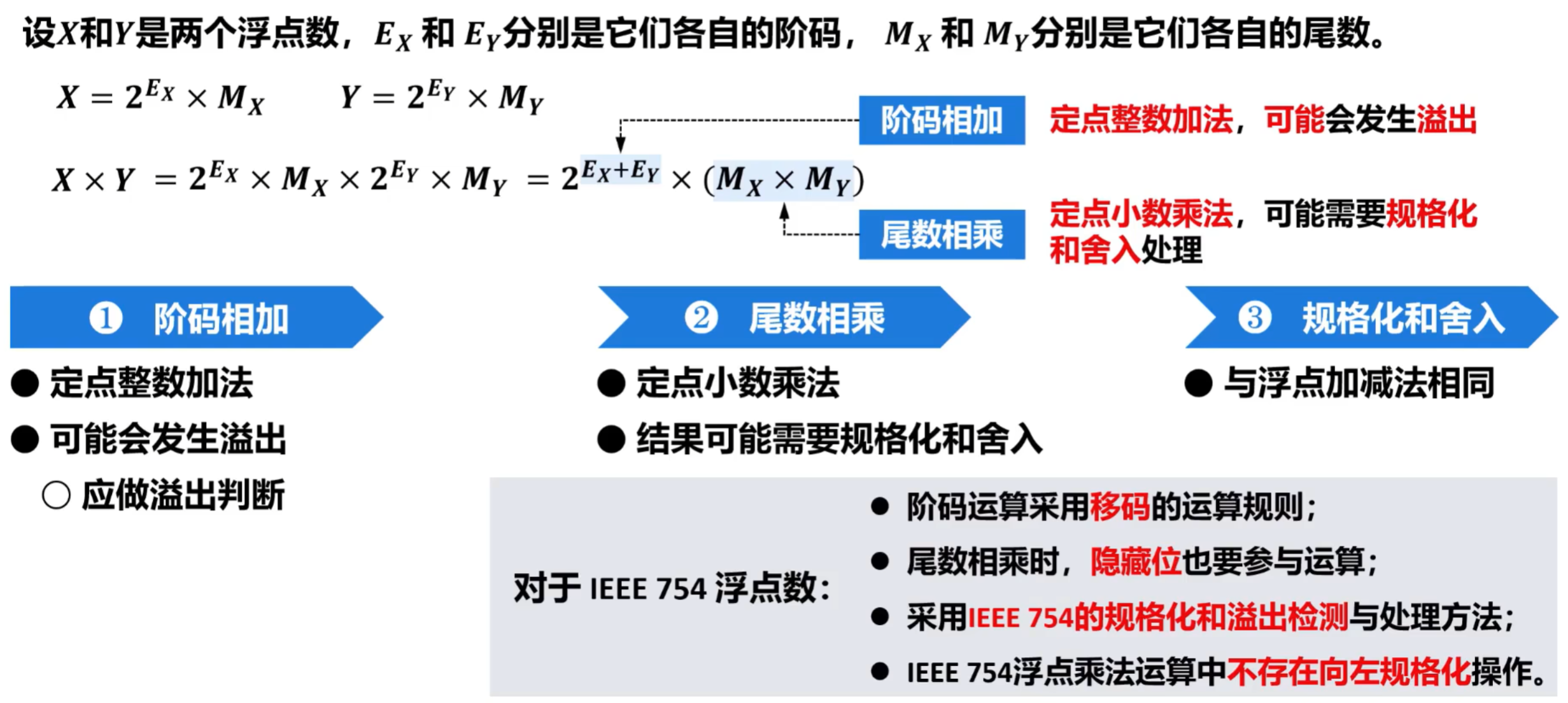
4)浮点除法运算
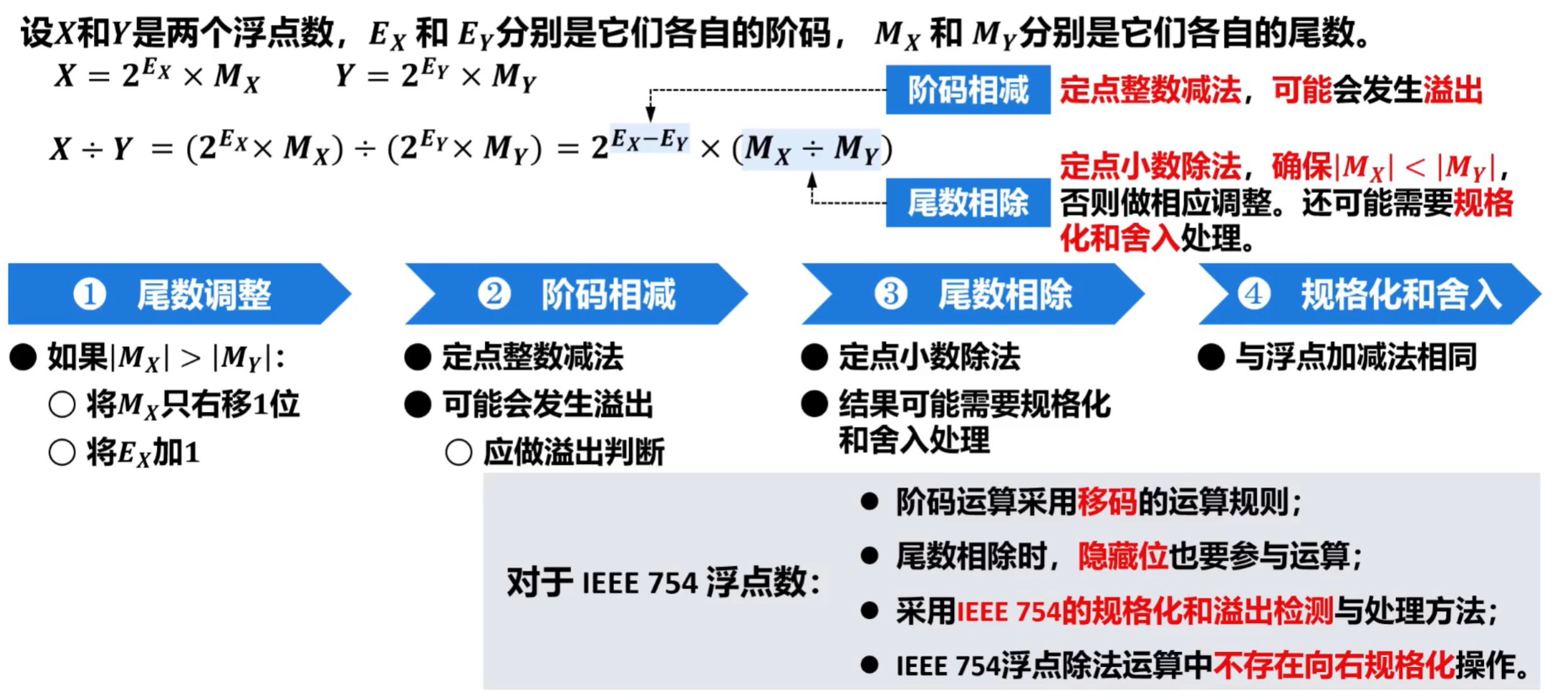
5、运算器
1)运算器的概念
计算机中的各类算术运算都可以利用基本的定点加法运算和移位运算来实现。将实现加法运算、移位运算、逻辑运算以及各种算术运算所需的数字逻辑电路集成在一起,就可以构成CPU中的运算器。
运算器通常分为两种:定点运算器和浮点运算器。
- 定点运算器:以算术逻辑单元ALU为核心,可以进行定点数的移位、算术、逻辑运算。
- 浮点运算器:以浮点运算单元FPU为核心,负责进行浮点数的算术运算。
浮点运算比定点运算复杂得多,因此,实现浮点运算的逻辑电路也比较复杂,早期将其实现路集成在一个单独的芯片中,目前大多集成在CPU内部。
2)算术逻辑单元ALU
浮点运算单元较为复杂,本节只介绍算术逻辑单元ALU
电路图及符号表示
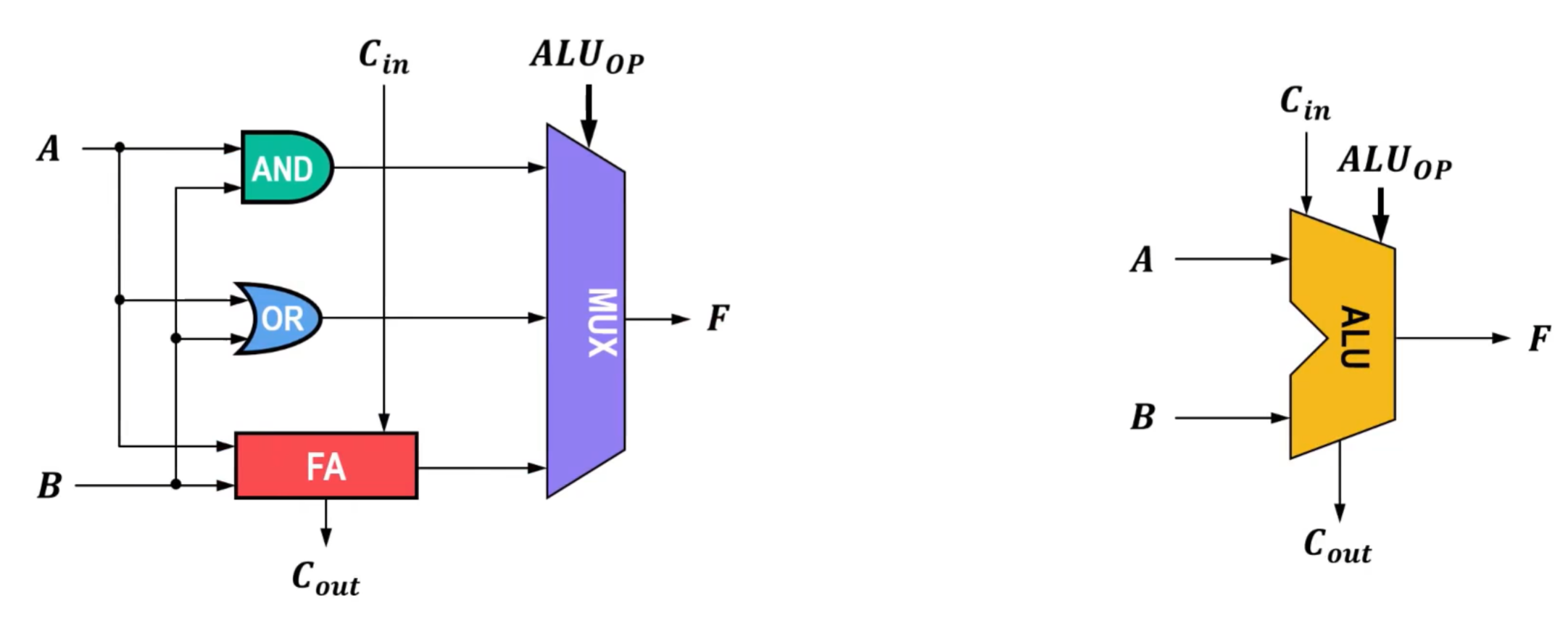
- 用与、或、加法3种运算的一位ALU,其中ALUOP作为控制,,输入信号控制输出结果,情况如下:
- 输入00,与运算结果从多路选择器MUX输出,则F=A*B
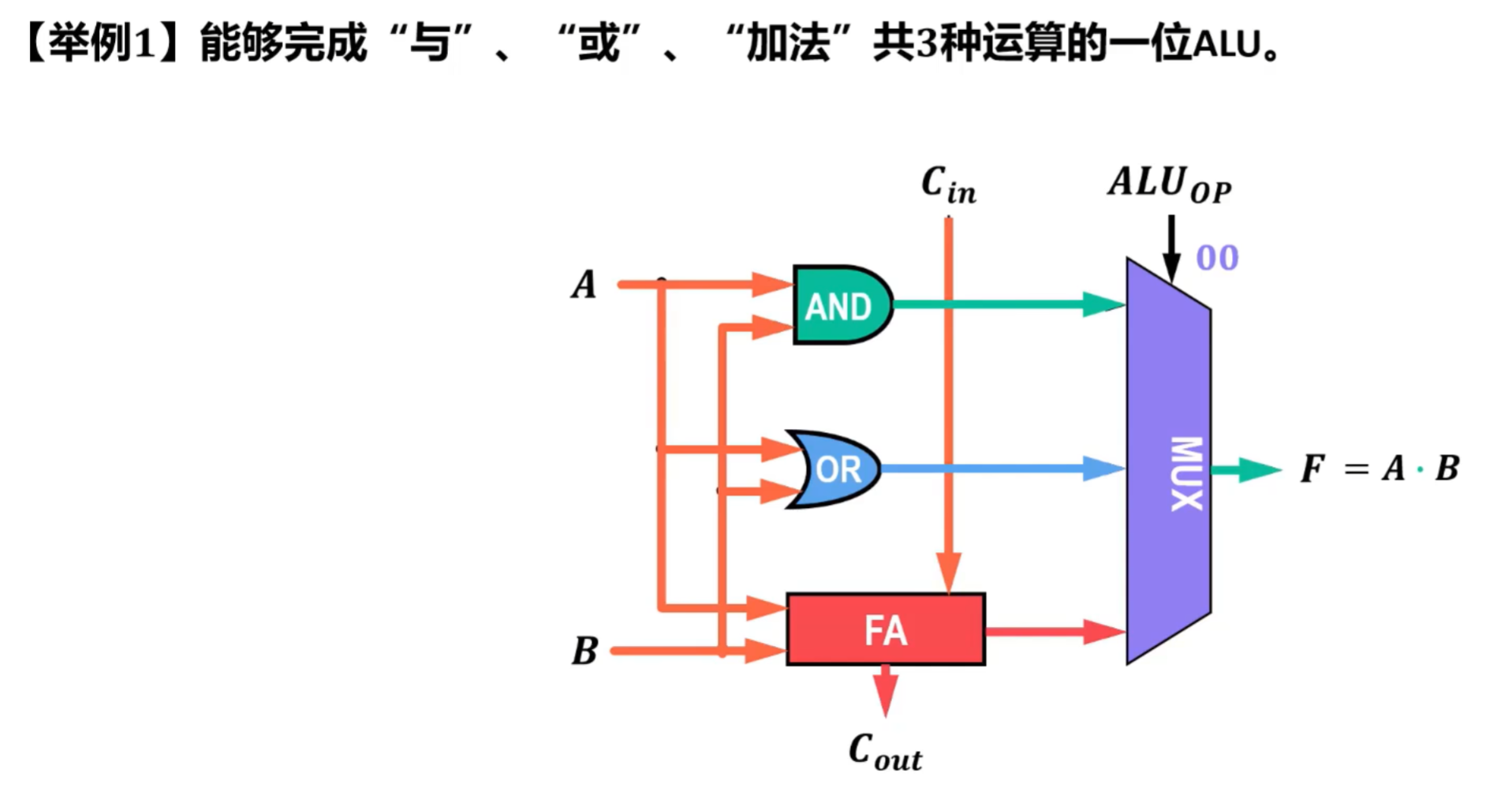
- 输入01,或运算结果从多路选择器MUX输出,则F=A+B
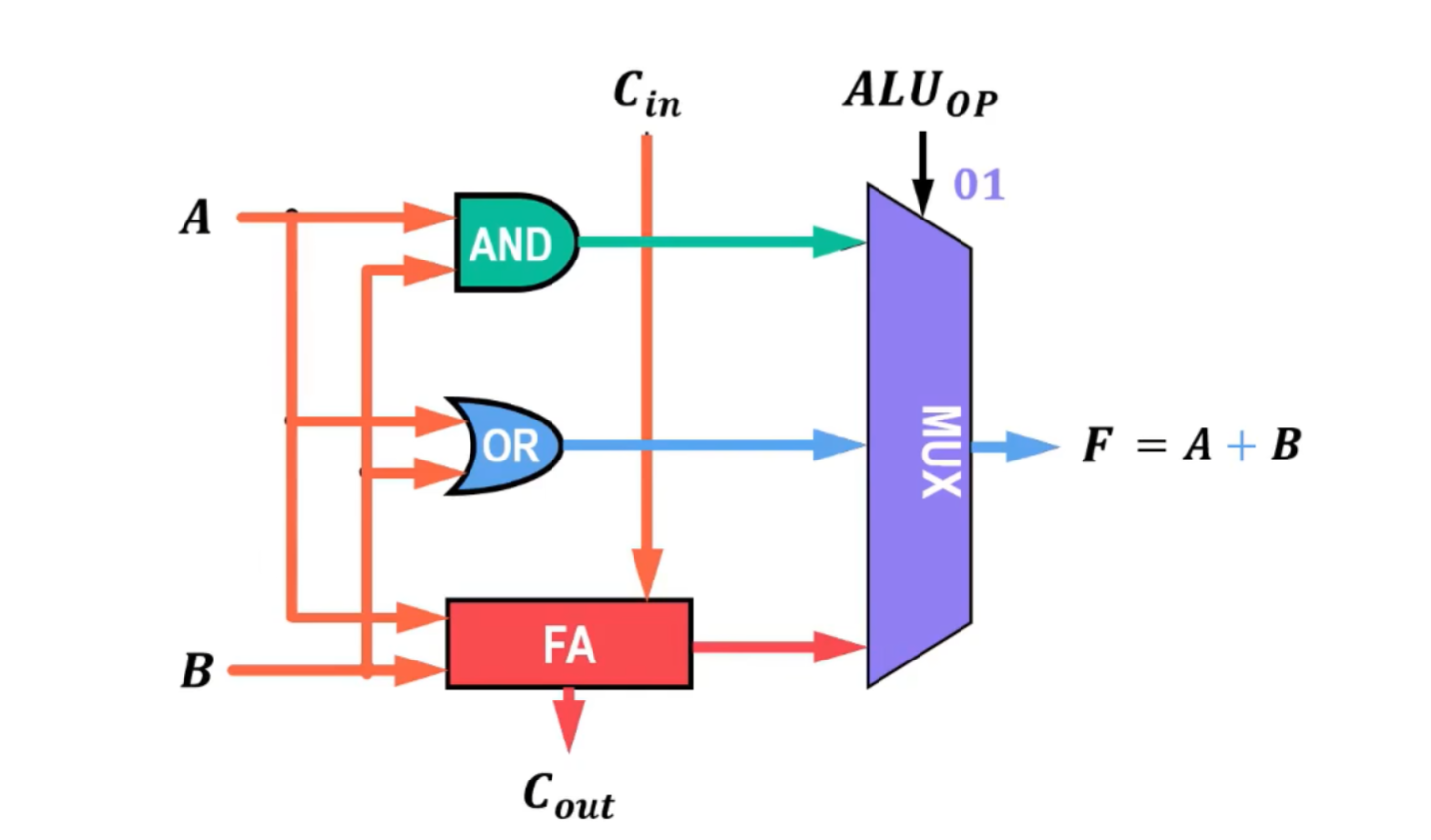
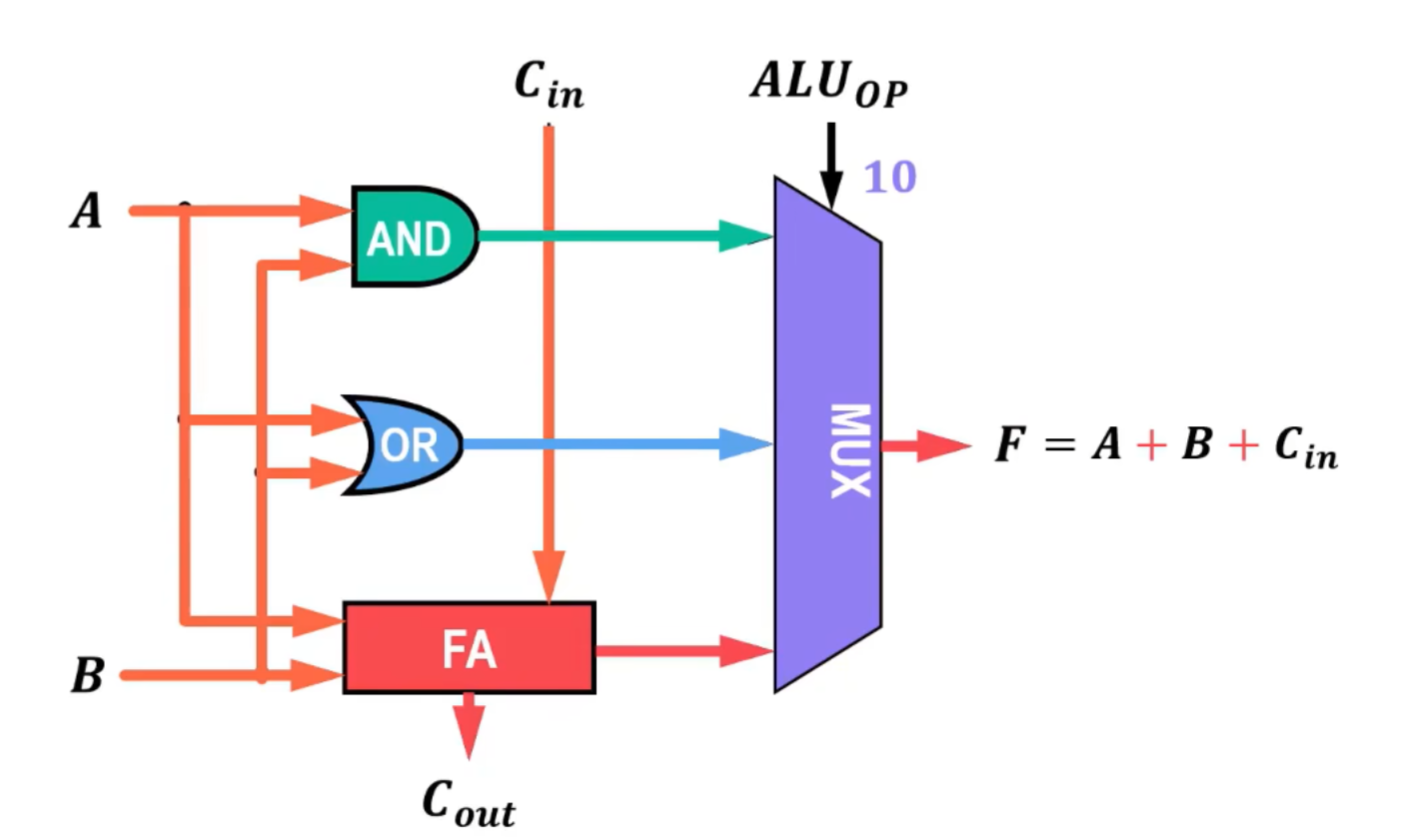
- 输入11,一位全加器的和数FA从多路选择器MUX输出,则F=A+B+Cin
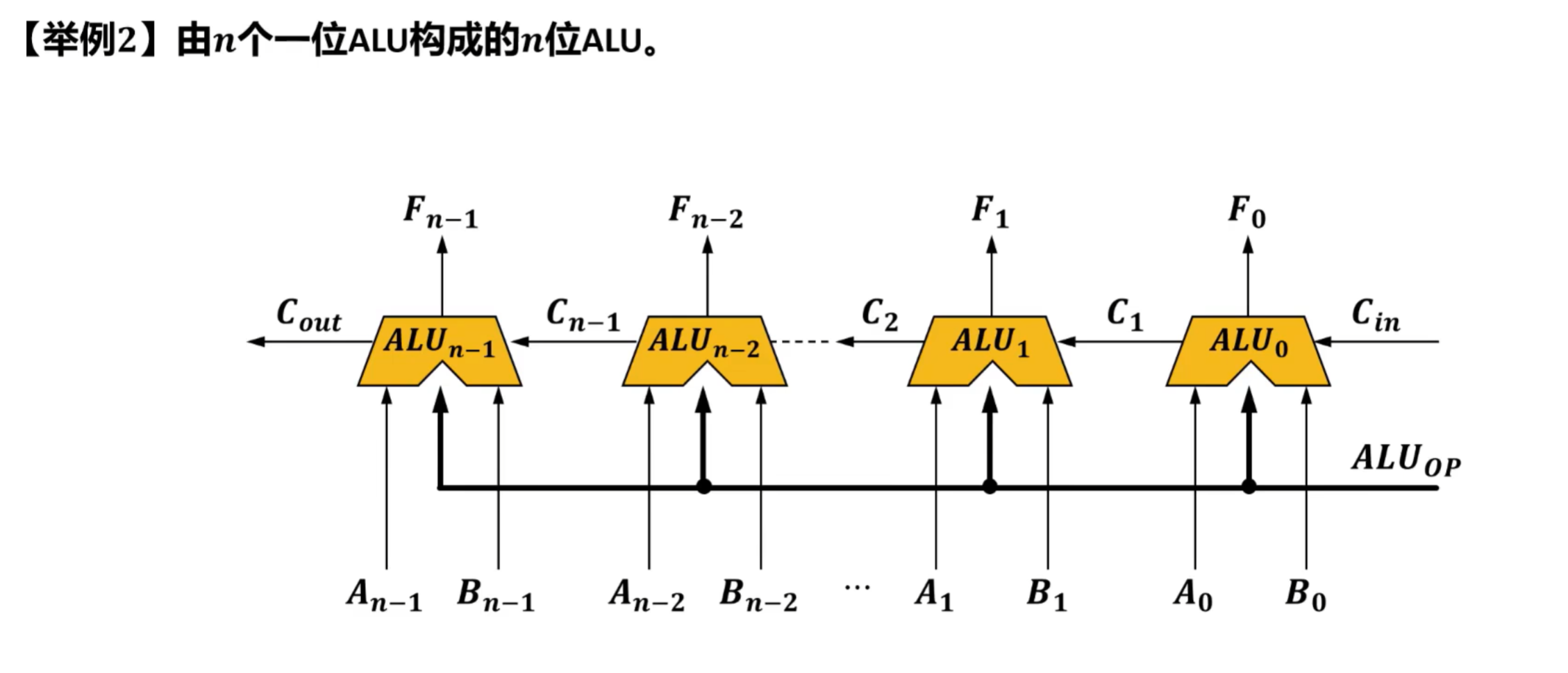
3)n个一位ALU构成的n位ALU
4)常见的状态标志位

不同计算机利用这些标志的方法和时机可能不同:
- 很多计算机将这些标志位暂存在一个状态寄存器中,为后续指令提供执行依据。例如,x86的EFLAGS寄存器,x86中的条件分支指令会根据标志位的不同进行不同的操作。
- 有些计算机没有状态寄存器,例如MIPS、RISC-V,其条件分支指令直接根据ALU当前状态标志位执行不同的分支。
50829171031676.png" alt=“image-20250829171031676” style=“zoom:33%;” />
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)