音乐信息检索简介 Pt. 2

BIGdd

39人浏览 · 2022-08-15 06:04:14

BIGdd · 2022-08-15 06:04:14 发布

分割与特征提取

(您可以在此处查看带有所有音频片段的版本

在part 1中,我们学习了一些基本的信号处理术语,以及如何加载和可视化歌曲。在这篇文章中,我们将讨论如何分解信号(段)并从中提取各种特征。然后,我们将对特征进行一些探索性分析,以便我们了解特征之间的相互作用。

为什么要对歌曲进行分段?

歌曲随时间变化很大。通过将这种异质信号分解成更同质的小片段,我们可以保留有关歌曲如何变化的信息。例如,假设我们有一些特征,例如“可跳舞性”。想象一首歌曲一开始非常安静和低能量,但随着歌曲的进展,它变成了一首成熟的蕾哈娜俱乐部国歌。如果我们只检查整首歌的平均可舞性,它可能低于这首歌的实际可舞性。这种背景和区别很重要,因为如果我们对歌曲的每个片段运行分类器或聚类算法,我们可以将该歌曲归类为俱乐部国歌,而不仅仅是(低于)平均水平。

使用起始检测对歌曲进行分段

信号的开始通常被描述为音符或其他声音的开始。这通常通过沿信号测量能量峰值来发现。如果我们找到能量峰值,然后回溯到局部最小值,我们就找到了一个起始点,并且可以将其用作歌曲片段的边界。

这里有一些很好的资源可以帮助你了解更多关于发病和发病检测的信息:https://musicinformationretrieval.com/onset_detection.html,https://en.wikipedia.org/wiki/Onset_(audio),https://www.music-ir.org/mirex/wiki/2018:Audio_Onset_Detection

%matplotlib inline
import librosa
import numpy as np
import IPython.display as ipd
import sklearn
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
plt.rcParams['figure.figsize'] = (16, 7)

默认情况下,onset_detect 返回与信号中的帧相对应的 frame 索引数组。我们其实

需要 sample 索引,以便我们可以使用这些索引巧妙地对信号进行切片和切块。我们将继续使用上一篇文章中的摇滚示例。

signal, sr = librosa.load('/Users/benjamindykstra/Music/iTunes/Led Zeppelin/Led Zeppelin IV/02 Rock & Roll.m4a')

# use backtrack=True to go back to local minimum
onset_samples = librosa.onset.onset_detect(signal, sr=sr, backtrack=True, units='samples')
print onset_samples.shape

(132,)

我们在歌曲中找到了 132 个片段。现在,让我们使用示例索引将歌曲拆分为子数组,如下所示:

[[segment 1],[segment 2],.....[segment n]]。每个段都有不同的长度,但是当我们为一个段计算特征向量时,特征向量将是标准大小。分割和计算每个段的特征后数据的最终维度将是(#段,#特征)。

# return np array of audio segments, within each segment is the actual audio data
prev_ndx = 0
segmented = []
for sample_ndx in onset_samples:
    # get the samples from prev_ndx to sample_ndx
    segmented.append(np.array(signal[prev_ndx:sample_ndx]))
    prev_ndx = sample_ndx
segmented.append(np.array(signal[onset_samples[-1]:])) # gets the last segment from the signal
segmented = np.array(segmented)

segmented.shape

(133,)

作为健全性检查,如果我们将所有段连接在一起,它的形状应该与原始信号相同。

print "difference in shapes: {}".format(signal.shape[0] - np.concatenate(segmented).shape[0])

difference in shapes: 0

一起听几段!

ipd.Audio(np.concatenate(segmented[25:30]), rate=sr)

或只是一个短段

ipd.Audio(segmented[21], rate=sr)

让我们定义一个更通用的分割函数以供以后使用

def segment_onset(signal, sr=22050, hop_length=512, backtrack=True):
    """
    Segment a signal using onset detection
    Parameters:
        signal: numpy array of a timeseries of an audio file
        sr: int, sampling rate, default 22050 samples per a second
        hop_length: int, number of samples between successive frames
        backtrack: bool, If True, detected onset events are backtracked to the nearest preceding minimum of energy
    returns:
        dictionary with attributes segemented and shape

    """
    # Compute the sample indices for estimated onsets in a signal
    onset_samples = librosa.onset.onset_detect(signal, sr=sr, hop_length=hop_length, backtrack=backtrack, units='samples')

    # return np array of audio segments, within each segment is the actual audio data
    prev_ndx = 0
    segmented = []
    for sample_ndx in onset_samples:
        segmented.append(np.array(signal[prev_ndx:sample_ndx]))
        prev_ndx = sample_ndx
    segmented.append(np.array(signal[onset_samples[-1]:]))
    return { 'data': np.array(segmented), 'shape': np.array(segmented).shape }

特征提取

既然我们有了分解歌曲的方法,我们希望能够从原始信号中获得一些特征。 Librosa 有很多功能可供选择。它们分为两类,频谱和节奏特征。频谱特征是与信号的频率、音高和音色有关的特征,其中节奏特征(您猜对了)为您提供有关信号节奏的信息。

特征提取的目标是为单个函数提供歌曲的单个片段,该函数返回该片段的计算特征数组

一些特征方法返回不同形状的数组,我们需要在我们的实现中考虑这些差异。例如,在计算片段的 Mel 频率倒谱系数时,返回形状为 (# of coefficients, # of frames in a segment)。由于我们假设一个片段是一个同质的信号片段,我们应该对所有帧的系数取平均值,这样我们就得到了一个 (# of coefficients, 1) 的形状。

首先,我将定义所有特征函数,然后我将解释它们添加/描述的信息。

def get_feature_vector(segment):
    '''
    Extract features for a given segment
    Parameters:
        segment: numpy array, a time series of audio data
    Returns:
        numpy array
    '''
    if len(segment) != 0:
        feature_tuple = (avg_energy(segment), avg_mfcc(segment), zero_crossing_rate(segment), avg_spectral_centroid(segment), avg_spectral_contrast(segment), bpm(segment))
        all_features = np.concatenate([feat if type(feat) is np.ndarray else np.array([feat]) for feat in feature_tuple])
        n_features = len(all_features)
        return all_features
    return np.zeros((30,)) # length of feature tuple


def avg_energy(segment):
    '''
    Get the average energy of a segment.
    Parameters:
        segment: numpy array, a time series of audio data
    Returns:
        float, the mean energy of the segment
    '''
    if len(segment) != 0:
        energy = librosa.feature.rmse(y=segment)[0]
        # returns (1,t) array, get first element
        return np.array([np.mean(energy)])


def avg_mfcc(segment, sr=22050, n_mfcc=20):
    '''
    Get the average Mel-frequency cepstral coefficients for a segment
    The very first MFCC, the 0th coefficient, does not convey information relevant to the overall shape of the spectrum. 
    It only conveys a constant offset, i.e. adding a constant value to the entire spectrum. We discard it.
    BE SURE TO NORMALIZE

    Parameters:
        segment: numpy array, a time series of audio data
        sr: int, sampling rate, default 22050
        n_mfcc: int, the number of cepstral coefficients to return, default 20.
    Returns:
        numpy array of shape (n_mfcc - 1,)
    '''
    if (len(segment) != 0):
        components = librosa.feature.mfcc(y=segment,sr=sr, n_mfcc=n_mfcc ) # return shape (n_mfcc, # frames)

        return np.mean(components[1:], axis=1)


def zero_crossing_rate(segment):
    '''
    Get average zero crossing rate for a segment. Add a small constant to the signal to negate small amount of noise near silent
    periods.

    Parameters:
        segment: numpy array, a time series of audio data
    Returns:
        float, average zero crossing rate for the given segment
    '''


    rate_vector = librosa.feature.zero_crossing_rate(segment+ 0.0001)[0] # returns array with shape (1,x)
    return np.array([np.mean(rate_vector)])


def avg_spectral_centroid(segment, sr=22050):
    '''
    Indicate at which frequency the energy is centered on. Like a weighted mean, weighting avg frequency by the energy.
    Add small constant to audio signal to discard noise from silence
    Parameters:
        segment: numpy array, a time series of audio data
        sr: int, sampling rate
    Returns:
        float, the average frequency which the energy is centered on.
    '''
    centroid = librosa.feature.spectral_centroid(segment+0.01, sr=sr)[0]
    return np.array([np.mean(centroid)])


def avg_spectral_contrast(segment, sr=22050, n_bands=6):
    '''
    considers the spectral peak, the spectral valley, and their difference in each frequency subband

    columns correspond to a spectral band

    average contrast : np.ndarray [shape=(n_bands + 1)]
    each row of spectral contrast values corresponds to a given
    octave-based frequency, take average across bands

    Parameters:
        segment: numpy array, a time series of audio data
        sr: int, sampling rate
        n_bands: the number of spectral bands to calculate the contrast across.
    Returns:
        numpy array shape (n_bands,)
    '''
    contr = librosa.feature.spectral_contrast(segment, sr=sr, n_bands=n_bands)
    return np.mean(contr, axis=1) # take average across bands

def bpm(segment, sr=22050):
    '''
    Get the beats per a minute of a song
    Parameters:
        segment: numpy array, a time series of audio data,
        sr: int, sampling rate
    Returns:
        int, beats per minute
    '''
    tempo = librosa.beat.tempo(segment) #returns 1d array [bpm]
    return np.array([tempo[0]])

所选特征对齐

能源:

片段的能量很重要,因为它给人一种片段的节奏和/或情绪的感觉。它实际上只是信号的均方根。

MFCC:

Mel频率倒谱系数传递有关歌曲音色的信息。音色描述了声音的“质量”。如果你想一想小号上的 A 音与钢琴上的 A 音有很大不同,这些差异是由于音色造成的。

过零率:

从字面上看,信号穿过水平轴的速率。它通常对应于信号中的事件,例如小军鼓或其他一些打击乐事件。

光谱质心:

我认为光谱质心实际上非常酷。它是信号和“质心”中频率幅度的加权平均值。它通常被认为是衡量声音亮度的指标。

光谱对比度:

基于倍频程的特征,它更直接地表示片段的频谱特征。再加上 MFCC 功能,它们可以提供有关信号的大量信息。

每分钟节拍:

提供有关歌曲速度和(某些)打击乐元素的信息。

现在我们实际上如何处理所有这些功能???我们可以用它们来集群!!

def extract_features(all_songs):
    '''
    all_songs is a list of dictionaries. Each dictionary contains the attributes song_name and data.
    The data are the segments of the song.
    '''
    all_song_features = []
    song_num = 0
    for song in all_songs:
        print "Processing {} with {} segments".format(song['song_name'], len(song['data']))
        song_name = song['song_name']
        segment_features = []
        for segment in song['data']:
            feature_vector = get_feature_vector(segment)
            segment_features.append(feature_vector)   


        song_feature_vector = np.array(segment_features)
        print "shape of feature vector for entire song: {}".format(song_feature_vector.shape)
        print "shape of segment feature vector: {}".format(song_feature_vector[0].shape)
        n_seg = song_feature_vector.shape[0]
        feature_length = song_feature_vector[0].shape[0]
        song_feature_vector = np.reshape(song_feature_vector, (n_seg, feature_length))

        all_song_features.append(song_feature_vector)
        song_num += 1
    all_feature_vector = np.vstack(all_song_features)
    return all_feature_vector

可视化两首截然不同的歌曲的特征

让我们看看 Led Zeppelin 的 Rock 'n Roll 和 Deadmau5 的 I Remember 的特点。

rock_n_roll = segment_onset(signal)
rock_n_roll['data'].shape

(133,)

feature_vec_rock = extract_features([{'song_name': '02 Rock & Roll.m4a', 'data': rock_n_roll['data']}])
feature_vec_rock.shape

Processing 02 Rock & Roll.m4a with 133 segments
shape of feature vector for entire song: (133, 30)
shape of segment feature vector: (30,)





(133, 30)

i_remember, sr = librosa.load('/Users/benjamindykstra/Music/iTunes/Deadmau5/Random Album Title/07 I Remember.m4a')
i_remember_segmented = segment_onset(i_remember)
feature_vec_remember = extract_features([{'song_name': '07 I Remember.m4a', 'data': i_remember_segmented['data']}])

Processing 07 I Remember.m4a with 1852 segments
shape of feature vector for entire song: (1852, 30)
shape of segment feature vector: (30,)

这两首歌很不一样

ipd.Audio(np.concatenate(i_remember_segmented['data'][:30]), rate= sr)

ipd.Audio(np.concatenate(rock_n_roll['data'][:20]), rate= sr)

我们需要将特征缩放到一个共同的范围,特征范围差异很大

col_names = ['energy'] + ["mfcc_" + str(i) for i in xrange(19)] + ['zero_crossing_rate', 'spectral_centroid'] + ['spectral_contrast_band_' + str(i) for i in xrange(7)] + ['bpm']
rnr = pd.DataFrame(feature_vec_rock, columns = col_names)
i_remember_df = pd.DataFrame(feature_vec_remember, columns = col_names)

min_max_scaler = sklearn.preprocessing.MinMaxScaler(feature_range=(-1, 1))
rnr_scaled = pd.DataFrame(min_max_scaler.fit_transform(feature_vec_rock), columns = col_names)
i_remember_scaled = pd.DataFrame(min_max_scaler.fit_transform(feature_vec_remember), columns = col_names)

features_scaled = pd.DataFrame(np.vstack((rnr_scaled, i_remember_scaled)), columns = col_names)

rnr_scaled.head()

活力

mfcc_0

mfcc_1

mfcc_2

mfcc_3

mfcc_4

mfcc_5

mfcc_6

mfcc_7

mfcc_8

...

零\交叉\速率

光谱_质心

光谱_对比度_波段_0

光谱_对比度_波段_1

光谱_对比度_波段_2

光谱_对比度_波段_3

光谱_对比度_波段_4

光谱_对比度_波段_5

光谱_对比度_波段_6

bpm

-1.0

0.122662

1.0

-0.516018

1.0

0.602426

1.0

0.540636

...

-1.0

0.827903

-1.0

-0.962739

-1.0

-0.538654

-0.503759

-0.242285

-0.648073

0.381125

-0.786313

-0.91164

-0.80649

-0.601857

-0.673427

-0.444300

-0.700703

...

0.604015

0.709584

0.99070

-0.187083

-0.375223

-0.307743

-0.114691

-0.157464

0.903511

-0.250000

-0.67639

-0.850079

0.421647

-0.732783

-0.226694

-0.404820

-0.733511

-0.860285

-0.528783

-0.503516

...

0.781001

0.850525

0.758635

-0.287418

-0.213330

-0.196650

-0.161395

0.109064

0.427987

-0.503759

-0.433760

-0.969241

0.401582

-0.620675

-0.46703

0.55861

-0.502694

-0.516944

0.55559

-0.147803

...

0.831207

0.924291

0.801980

0.226105

-0.535366

-0.160115

0.185044

0.142246

0.299663

-0.503759

-0.282242

-0.686175

0.325491

-0.689084

-0.86337

-0.26573

-0.474765

-0.471087

-0.126714

-0.212362

...

0.496496

0.731278

0.755725

0.126388

0.24655

-0.247040

0.625841

0.129373

0.113422

-0.503759

5行×30列

i_remember_scaled.head()

活力

mfcc_0

mfcc_1

mfcc_2

mfcc_3

mfcc_4

mfcc_5

mfcc_6

mfcc_7

mfcc_8

...

零\交叉\速率

光谱_质心

光谱_对比度_波段_0

光谱_对比度_波段_1

光谱_对比度_波段_2

光谱_对比度_波段_3

光谱_对比度_波段_4

光谱_对比度_波段_5

光谱_对比度_波段_6

bpm

0.58494

-0.647307

0.539341

-0.121477

0.541506

0.437682

-0.272703

0.223814

-0.16933

-0.48312

...

-0.114140

0.491343

0.292913

0.271760

0.192199

-0.773597

-0.625672

-0.67422

0.317499

-0.676113

-0.5999

-0.534543

-0.160968

-0.374121

0.505839

0.547995

-0.180246

0.333693

-0.98430

0.29649

...

-0.273774

0.318984

0.266204

-0.26715

-0.369555

-0.694350

-0.538811

-0.494475

0.247816

-0.676113

-0.14792

-0.465639

-0.168007

-0.570869

0.449955

0.559676

-0.168267

0.279917

-0.95737

-0.53418

...

-0.327139

0.187170

0.507119

0.38864

-0.463672

-0.728928

-0.451278

-0.269847

0.223124

-0.676113

0.127275

-0.410650

0.45166

-0.534741

0.485562

0.635807

-0.145189

0.292996

-0.3948

0.145229

...

-0.474190

0.109161

0.216147

-0.372901

-0.184409

-0.732067

-0.453334

-0.383937

0.103847

-0.676113

0.99671

-0.368250

0.332703

-0.435360

0.505144

0.570220

-0.128529

0.181684

-0.68506

-0.32707

...

-0.539708

0.116126

0.209937

-0.236042

-0.115957

-0.544722

-0.496779

-0.378822

-0.68973

-0.676113

5行×30列

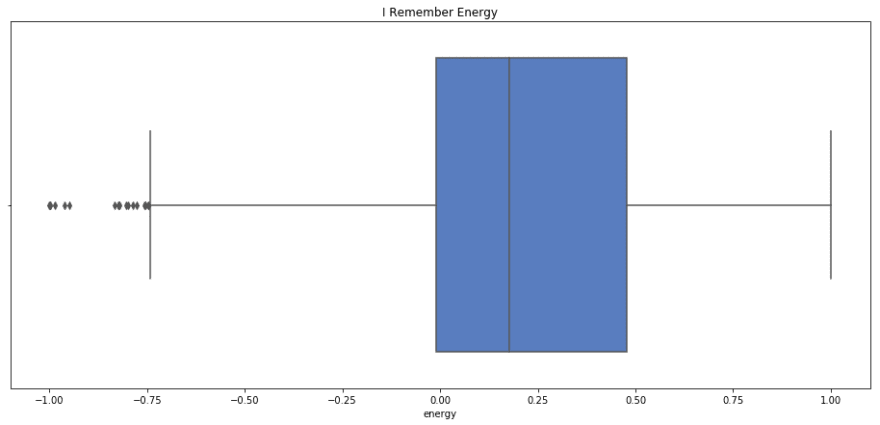
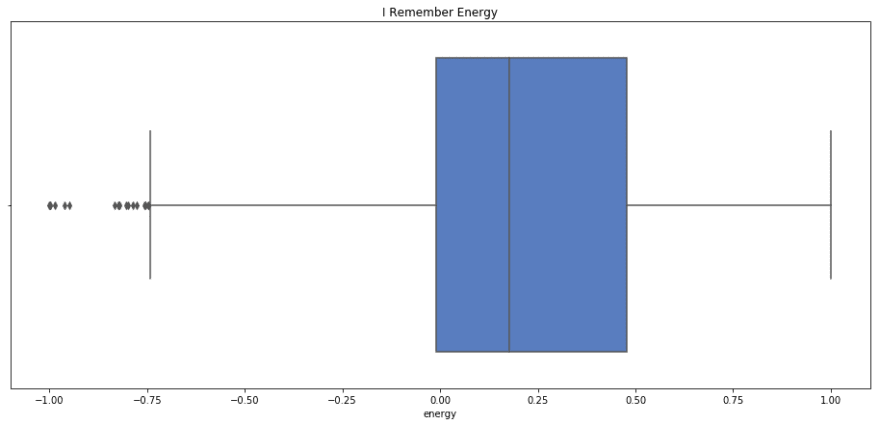
让我们看一下能量的描述性统计

sns.boxplot(x=i_remember_scaled.energy, palette='muted').set_title('I Remember Energy');
plt.show();
print i_remember_scaled.energy.describe()
sns.boxplot(rnr_scaled.energy).set_title('Rock n Roll Energy');
plt.show();
print rnr_scaled.energy.describe()

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--O3ZLHFWh--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/a30q7j785f1zosjce5qs.png)

count    1852.000000
mean        0.184555
std         0.373220
min        -1.000000
25%        -0.009499
50%         0.176136
75%         0.478511
max         1.000000
Name: energy, dtype: float64

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--ZL979uKI--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/3wjy03bzm2kcvew2uefy.png)

count    133.000000
mean       0.354920
std        0.391389
min       -1.000000
25%        0.117536
50%        0.439199
75%        0.639228
max        1.000000
Name: energy, dtype: float64

我记得平均能量和中值能量较低,但与摇滚乐相似。我想说这很合适,因为我记得几乎有一种忧郁的能量,而摇滚真的让你站起来动起来。

过零率和BPM呢?

由于过零率和 bpm 与打击乐事件的相关性非常高,我预测具有较高 BPM 的歌曲将具有较高的过零率

print 'Rock n Roll average BPM: {}'.format(rnr.bpm.mean())
print 'Rock n Roll average Crossing Rate: {}'.format(rnr.zero_crossing_rate.mean())
print 'I Remember average BPM: {}'.format(i_remember_df.bpm.mean())
print 'I Remember average Crossing Rate: {}'.format(i_remember_df.zero_crossing_rate.mean())

Rock n Roll average BPM: 150.784808472
Rock n Roll average Crossing Rate: 0.14643830815
I Remember average BPM: 136.533708743
I Remember average Crossing Rate: 0.0362864360563

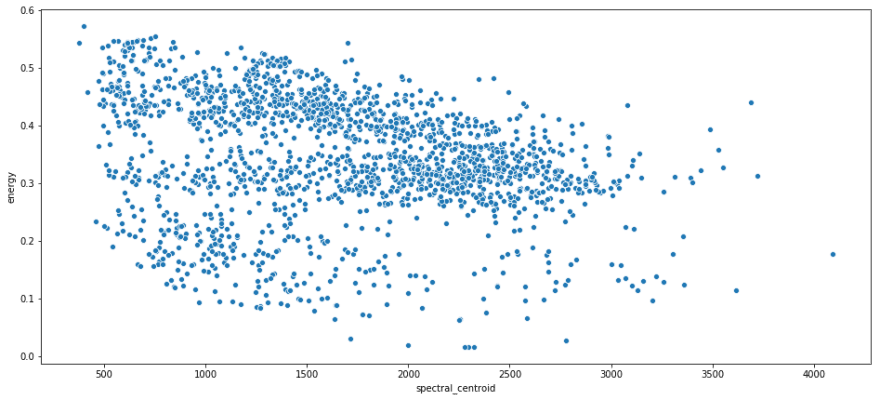
一些散点图在 x 轴上具有光谱质心,在 y 轴上具有能量。

sns.scatterplot(x = rnr.spectral_centroid, y = rnr.energy);
plt.show();
sns.scatterplot(x = i_remember_df.spectral_centroid, y = i_remember_df.energy );
plt.show();

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--l6bQhNG9--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/0g23eb4963drp956me7f.png)

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--LmtGdjsr--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/aer4z6fko64qlfko4dy7.png)

回想一下,光谱质心是给定片段的光谱“质心”所在的位置。这意味着它正在挑选一段的主导频率。我喜欢这个,因为它表明片段的频率与其能量之间没有真正的关系。他们都在贡献独特的信息。

使用 k 方法构建标签和集群!

song_labels = np.concatenate([np.full((label_len), i) for i, label_len in enumerate([len(rnr), len(i_remember_df)])])

model = sklearn.cluster.KMeans(n_clusters=3)

labels = model.fit_predict(features_scaled)

plt.scatter(features_scaled.zero_crossing_rate[labels==0], features_scaled.energy[labels==0], c='b')
plt.scatter(features_scaled.zero_crossing_rate[labels==1], features_scaled.energy[labels==1], c='r')
plt.scatter(features_scaled.zero_crossing_rate[labels==2], features_scaled.energy[labels==2], c='g')
plt.xlabel('Zero Crossing Rate (scaled)')
plt.ylabel('Energy (scaled)')
plt.legend(('Class 0', 'Class 1', 'Class 2'))

<matplotlib.legend.Legend at 0x13f054f10>

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--O_V8NDnN--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/nrsr49kfk0kg5a9l24sy.png)


unique_labels, unique_counts = np.unique(model.predict(rnr_scaled), return_counts=True)
print unique_counts
print 'cluster for rock n roll: ', unique_labels[np.argmax(unique_counts)]

[29  9 95]
cluster for rock n roll:  2

unique_labels, unique_counts = np.unique(model.predict(i_remember_scaled), return_counts=True)
print unique_counts
print 'cluster for I remember: ', unique_labels[np.argmax(unique_counts)]

[396 877 579]
cluster for I remember:  1

我怀疑过零率和能量不是集群的决定因素:)

我们实际上可以收听分配了特定标签的片段

请注意,这些不一定是连续的段

首先让我们看看我记得

i_remember_clusters = model.predict(i_remember_scaled)
label_2_segs = i_remember_segmented['data'][i_remember_clusters==2]
label_1_segs = i_remember_segmented['data'][i_remember_clusters==1]
label_0_segs = i_remember_segmented['data'][i_remember_clusters==0]

几乎所有这些都包含一些人声

ipd.Audio(np.concatenate(label_2_segs[:50]), rate = sr)

这些是较轻的部分,主要是合成器

ipd.Audio(np.concatenate(label_1_segs[:50]), rate = sr)

0 个标签似乎是重低音和打击乐部分

ipd.Audio(np.concatenate(label_0_segs[:50]), rate = sr)

现在摇滚

rnr_clusters = model.predict(rnr_scaled)

rock_label_2_segs = rock_n_roll['data'][rnr_clusters==2]
rock_label_1_segs = rock_n_roll['data'][rnr_clusters==1]
rock_label_0_segs = rock_n_roll['data'][rnr_clusters==0]

同样,更高的频率,包括人声。很多连续的片段都包含在这个类中。

ipd.Audio(np.concatenate(rock_label_2_segs[10:40]), rate = sr)

            <audio controls="controls" >
                Your browser does not support the audio element.
            </audio>

较轻的声音,小调人声,最终鼓独奏的一部分

ipd.Audio(np.concatenate(rock_label_1_segs), rate = sr)

            <audio controls="controls" >
                Your browser does not support the audio element.
            </audio>

所有 John Bonham 都在这里(只有鼓)。类似于我记得标签 0 对应于重低音

ipd.Audio(np.concatenate(rock_label_0_segs), rate = sr)

            <audio controls="controls" >
                Your browser does not support the audio element.
            </audio>

结论

我们使用了两首非常不同的歌曲来构建频谱和节奏特征的向量。然后,我们通过箱线图、散点图和描述性统计检查了这些特征如何相互关联。使用这些功能,我们将歌曲的不同片段聚集在一起,以比较不同簇的声音。

需要更多的探索来弄清楚如何为具有代表性的整首歌曲分配特征值。通过做更多的工作,就有可能获得整首歌曲的摘要特征。稍后再详细介绍!

剩下的只是对不同特征的一些无向探索

print rnr_scaled[rnr_clusters==0]['spectral_centroid'].describe()
print rnr_scaled[rnr_clusters==1]['spectral_centroid'].describe()
print rnr_scaled[rnr_clusters==2]['spectral_centroid'].describe()

count    9.000000
mean    -0.360693
std      0.250294
min     -1.000000
25%     -0.370240
50%     -0.280334
75%     -0.260073
max     -0.148394
Name: spectral_centroid, dtype: float64
count    29.000000
mean      0.066453
std       0.363603
min      -0.483240
25%      -0.211871
50%       0.012854
75%       0.156281
max       0.814435
Name: spectral_centroid, dtype: float64
count    95.000000
mean      0.354971
std       0.261067
min      -0.669203
25%       0.218433
50%       0.318239
75%       0.427016
max       1.000000
Name: spectral_centroid, dtype: float64

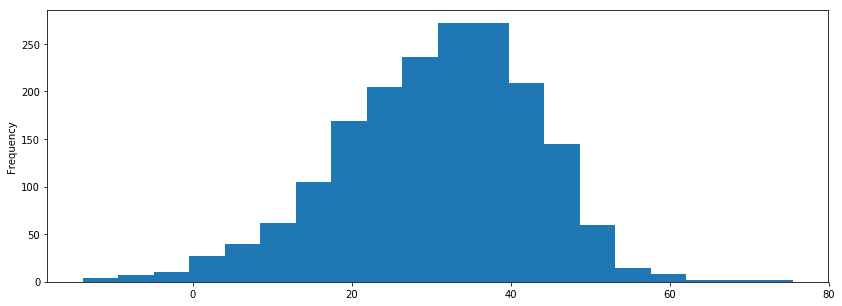
i_remember_df['mfcc_2'].plot.hist(bins=20, figsize=(14, 5))

<matplotlib.axes._subplots.AxesSubplot at 0x139127290>

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--o-W9HM-8--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev .s3.amazonaws.com/i/18dry1k6x7gl5i3fepcm.png)

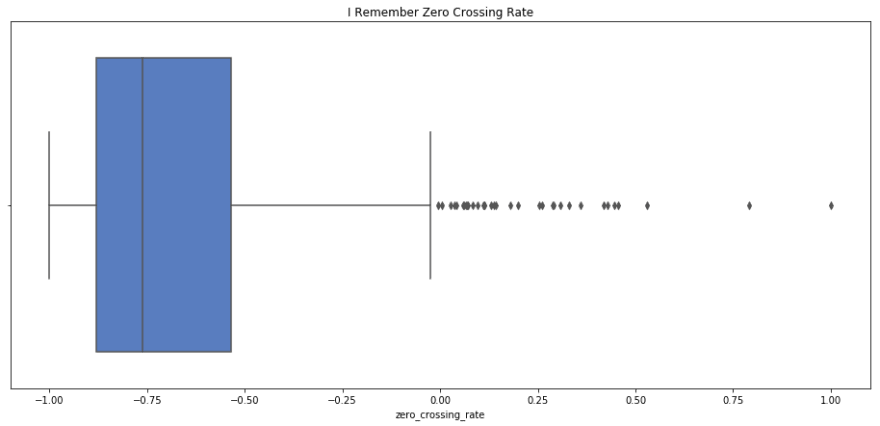
sns.boxplot(x=i_remember_scaled.zero_crossing_rate, palette='muted').set_title('I Remember Zero Crossing Rate');
plt.show();
print i_remember_scaled.zero_crossing_rate.describe()
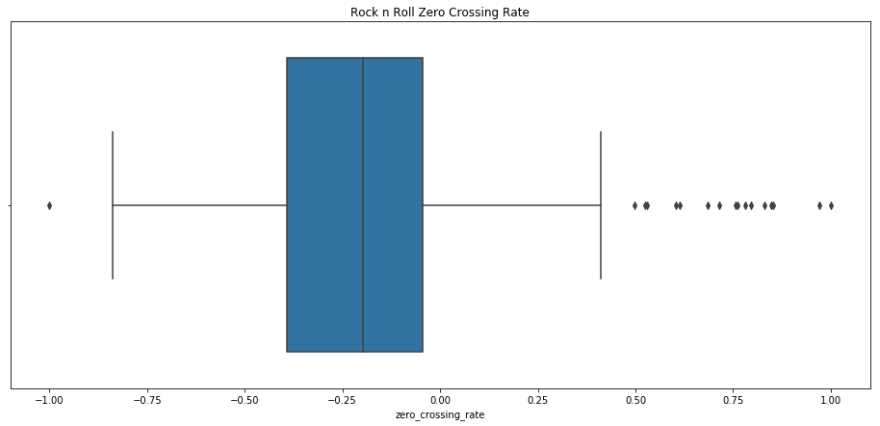
sns.boxplot(rnr_scaled.zero_crossing_rate).set_title('Rock n Roll Zero Crossing Rate');
plt.show();
print rnr_scaled.zero_crossing_rate.describe()

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--3YnEAEyj--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/8pgo0zrgimpfgce13v54.png)

count    1852.000000
mean       -0.683760
std         0.255792
min        -1.000000
25%        -0.880912
50%        -0.762325
75%        -0.535427
max         1.000000
Name: zero_crossing_rate, dtype: float64

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--KTCeQV5---/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3。 amazonaws.com/i/gzzej1qm1nx0so1uw4pf.png)

count    133.000000
mean      -0.152444
std        0.421004
min       -1.000000
25%       -0.393116
50%       -0.198213
75%       -0.045042
max        1.000000
Name: zero_crossing_rate, dtype: float64

print rnr.zero_crossing_rate.describe()
print i_remember_df.zero_crossing_rate.describe()

count    133.000000
mean       0.146438
std        0.072255
min        0.000977
25%        0.105133
50%        0.138583
75%        0.164871
max        0.344226
Name: zero_crossing_rate, dtype: float64
count    1852.000000
mean        0.036286
std         0.025857
min         0.004319
25%         0.016357
50%         0.028345
75%         0.051281
max         0.206489
Name: zero_crossing_rate, dtype: float64

print rnr.bpm.describe()
print i_remember_df.bpm.describe()

count    133.000000
mean     150.784808
std       31.793864
min       86.132812
25%      135.999178
50%      135.999178
75%      172.265625
max      287.109375
Name: bpm, dtype: float64
count    1852.000000
mean      136.533709
std         7.140772
min       112.347147
25%       135.999178
50%       135.999178
75%       135.999178
max       258.398438
Name: bpm, dtype: float64

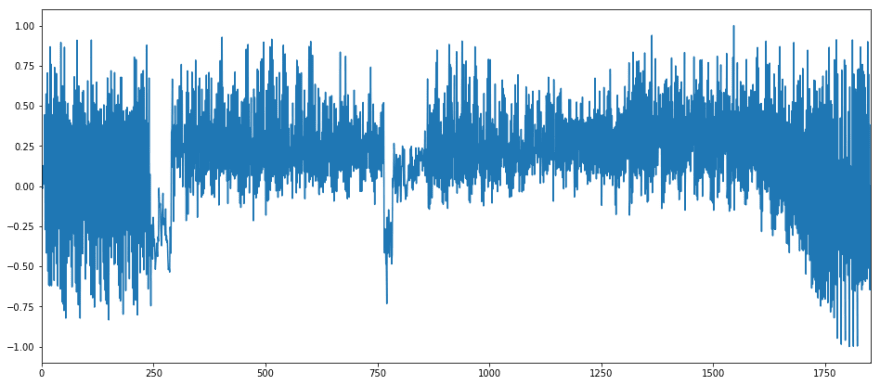
# rnr_scaled['energy'].plot();
i_remember_scaled['energy'].plot();
# rnr_scaled['zero_crossing_rate'].plot();
# rnr_scaled['spectral_centroid'].plot();
# rnr_scaled['mfcc_4'].plot();
plt.show()

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--yLExc1ug--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/juufxpnrgw0osq45xssy.png)

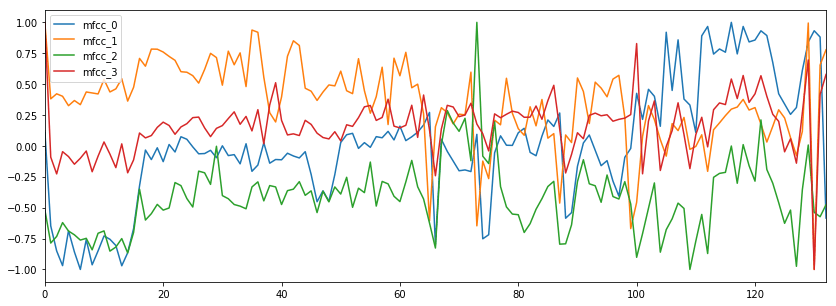
rnr_scaled[['mfcc_' + str(i) for i in xrange(4)]].plot();
plt.show();

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--zJvR4ORB--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/h8bkibxh72kgmvga6m7s.png)

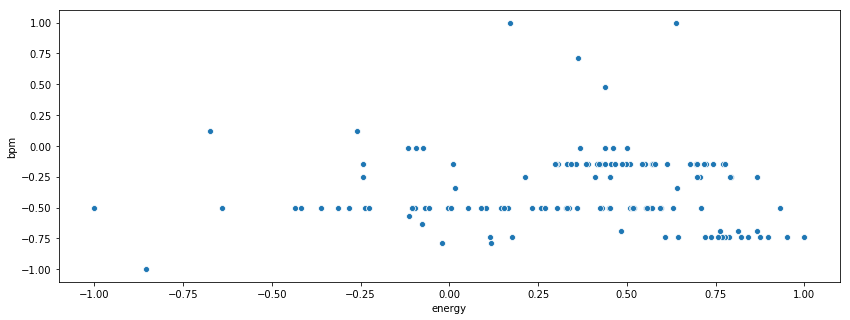
sns.scatterplot(x=rnr_scaled['energy'], y = rnr_scaled['bpm'])

<matplotlib.axes._subplots.AxesSubplot at 0x131c69ad0>

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--JgEUqjwf--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3.amazonaws .com/i/k228q960p1g25uravyz2.png)

sns.pairplot(rnr_scaled[['mfcc_' + str(i) for i in xrange(5)]], palette='pastel')

<seaborn.axisgrid.PairGrid at 0x15f503c10>

[ png ](https://res.cloudinary.com/practicaldev/image/fetch/s--S8Y6WH-q--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://thepracticaldev.s3 .amazonaws.com/i/sjz7hn9d1z7s3rfs9r0t.png)

向你推荐>>>开发者社区

华为、百度、京东云现已入驻，来创建你的专属开发者社区吧！

更多推荐

关于 Jupyter 笔记本最糟糕的五件事

我曾经喜欢 Jupyter。我仍然认为它们是许多任务的绝佳工具,例如探索性数据分析和轻松轻松地向同事展示见解。然而,虽然它们有时非常适合数据科学,但有时却令人头疼。像任何软件工具一样,它们也有其缺点。以下是 Jupyter Notebooks 用于数据科学的五个最糟糕的事情: 1.练习良好的代码版本控制几乎是不可能的 Jupyter Notebooks 对于代码版本控制来说很糟糕。问题是它们存储为

大数据

2023 年流行的大数据和数据科学角色

数据科学和大数据提供了广泛的职业前景。涉及数据的角色的扩展伴随着数据科学的出现。它是当今最流行和最前沿的技术应用领域之一,这是有道理的。数据科学目前可能是最好的就业市场。与此同时,这一发展中的主题正在改变众多业务和技术。随着所有垂直领域的行业越来越受数据驱动,就业市场和必要的技能受到影响。随着我们学习新的数据接触点和评估方法,我们生活的社会、日常生活和国家经济越来越依赖数据。这是大数据和数据科学能

大数据

数据科学的主要组成部分和特点

数据科学是十年来增长最快、最具挑战性和高薪的工作之一。那么,究竟什么是数据科学?数据科学是一个跨学科领域,它结合了统计学、计算机科学和机器学习算法,以从结构化和非结构化数据中获得洞察力。据《经济时报》报道,尽管供应增长缓慢,但印度对通过数据科学课程认证的各行业数据科学专业人员的需求增长了 400% 以上。数据科学的组成部分 1\。数据探索这是最关键的一步,因为它花费的时间最多。数据探索消耗了大