在使用线性回归模型时,对数转换非常有用。它们非常有助于纠正数据的偏度,并使分布更加正常。

Alexander Bailey和我在金县的房价数据集上工作,以开发解释价格变化的线性回归模型。

我们尝试对几个连续变量进行对数转换,但将对数转换应用于距主要中心位置的距离集:西雅图市中心、贝尔维尤市中心和南湖联盟,我们获得了最佳结果。到这些位置中的每一个的距离都以英里表示。

让我们看看其中一个变量:距西雅图市中心的距离(以英里为单位)。这是分布在对数转换前后的样子:

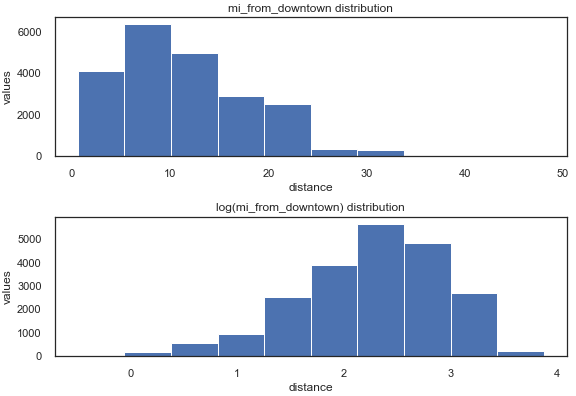[](https://res.cloudinary.com/practicaldev/image/fetch/s--ROzFyo8H--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://github .com/AnnaLara/dsc-1-final-project/raw/master/dis_downtown_distr.png)

我们可以看到,对数变换校正了偏度,使分布更正态,有利于线性回归模型的性能。通过取参数值的自然对数,我们能够改进模型的指标:在一次模型拟合迭代中,R 平方从 0.627 到 0.686,MAE 从134016.02 到131342.48。

在距贝尔维尤市中心距离较远的情况下,通过取变量值的自然对数,分布也得到了显着改善:

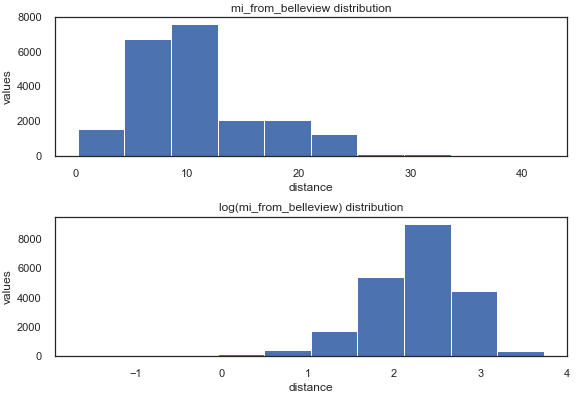[](https://res.cloudinary.com/practicaldev/image/fetch/s--77-KKXtM--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https:// /github.com/AnnaLara/dsc-1-final-project/raw/master/dis_bellvue_distr.png)

与 South Lake Union 参数的距离进行对数变换后的分布变化:

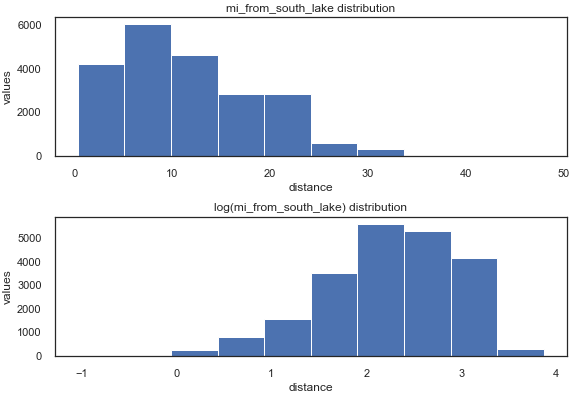[](https://res.cloudinary.com/practicaldev/image/fetch/s--xipCWx5o--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https:// github.com/AnnaLara/dsc-1-final-project/raw/master/dis_s_lake_union_distr.png)

线性回归模型中的对数变换距离参数

我们最终的房价模型侧重于对最高约 110 万美元的价格进行预测。与西雅图市中心、贝尔维尤市中心和南湖联盟的距离是价格的最强预测因素之一。

以下是我们模型中距离值的系数:

系数名称

价值

'mi_from_downtown_log'

210431.83668516215

'mi_from_bellevue_log'

-109855.7636174455

'mi\from\south\lake_log'

-294919.7693134867

系数值的一般解释是,假设模型中的其他变量保持不变,“mi_from_downtown_log”变量增加一个单位,将导致房价平均上涨 210,431.84 美元.然而,困难在于解释变量是对数转换的。

距离市区参数

假设其他变量保持不变,让我们模拟西雅图市中心距离的增加(以英里为单位)将如何影响房价。

首先,让我们生成一个从 1 到 100 的数字数组,表示与西雅图市中心的距离增加。下一步是获取这些数字的对数值,生成一个范围从 0 到 1.6 的数组。然后,我们使用线性回归模型中的系数 210,431.84 计算每个 log(x) 值的 y 值(即我们的预测价格)。

miles_range = np.arange(1, 101)

miles_range_log = np.log(miles_range)

y = 210431.83668516215 * miles_range_log

下图表示 y 和 log(x) 之间的关系与 y 和 x 之间的关系:

fig, axs = plt.subplots(2, 1, constrained_layout=True)

axs[0].plot(miles_range_log, y) axs[0].set_title('Log transformed variable') axs[0].set_xlabel('log(mi_from_downtown)') axs[0].set_ylabel('price')

axs[1].plot(miles_range, y) axs[1].set_title('Raw data') axs[1].set_xlabel('mi_from_downtown') axs[1].set_ylabel('price');

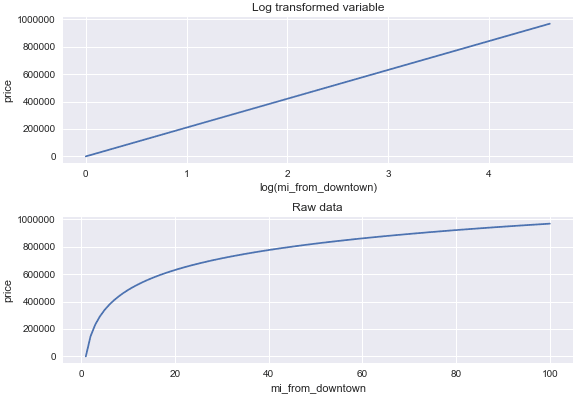[](https://res.cloudinary.com/practicaldev/image/fetch/s--khmPpAIS--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https:// github.com/AnnaLara/dsc-1-final-project/raw/master/dis_downtown_raw_vs_log.png)

我们可以看到,对这个变量进行了对数转换,将关系从指数转换为线性,这有助于提高线性回归的指标。

有趣的是,在距西雅图市中心距离的情况下,相关性是正的,这与我们的预期相反。然而,房价与贝尔维尤市中心和南湖联盟的距离呈负相关。解释可能是人们更愿意远离西雅图市中心,而不是靠近其他地点。

距贝尔维尤市中心距离参数

根据我们的模型,系数为 -109855.76。

让我们构建一个 y 值数组:

y_bellevue = -109855.76 * miles_range_log

绘制 log(x) 和 x vs y:

fig, axs = plt.subplots(2, 1, constrained_layout=True)

axs[0].plot(miles_range_log, y_bellevue) axs[0].set_title('Log transformed variable') axs[0].set_xlabel('log(mi_from_bellevue)') axs[0].set_ylabel('price')

axs[1].plot(miles_range, y_bellevue) axs[1].set_title('Raw data') axs[1].set_xlabel('mi_from_bellevue') axs[1].set_ylabel('price');

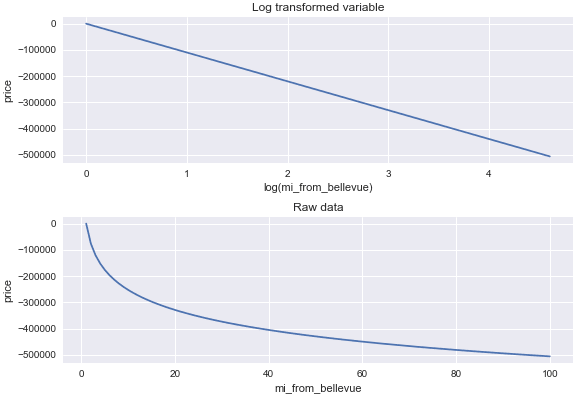[](https://res.cloudinary.com/practicaldev/image/fetch/s--TxEu-w-c--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https: //github.com/AnnaLara/dsc-1-final-project/raw/master/dis_bellvue_raw_vs_log.png)

这里的关系更符合逻辑:房子离贝尔维尤越远,它的价格就越低。

距离南湖联合参数

此参数的系数为 -294919.77,这是所有三个距离参数中最显着的。

计算具有 y 值的数组:

y_s_lake_union = -294919.7693134867 * miles_range_log

x 和 log(x) 与 y 的可视化:

[](https://res.cloudinary.com/practicaldev/image/fetch/s--cNETzIOS--/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https:// github.com/AnnaLara/dsc-1-final-project/raw/master/dis_south_late_union_raw_vs_log.png)

解释结果

当对数据集进行日志转换时,可能很难向非技术人员解释模型的工作原理。下面是如何使用我们的模型示例来完成它。

让我们看看与南湖联盟的距离,因为它是三个距离参数中最重要的变量。该值的系数为 -294919.76,在非对数转换变量的情况下,这意味着与南湖联盟的距离增加 1 英里将导致平均价格下降 294,919.76 美元。

但是,价格的值是对数转换的,所以我们不能使用这种增加 1 个单位的技术。在对数数据转换的情况下,我们可以谈论百分比变化。

要找出目标价格的涨幅是多少,让我们看一下等式:

price(x1) - price(x0) u003d coef * log(x1) - coef*log(x0) u003d coef * (log(x1) - log(x0)) u003d coef * log(x1/ x0)

因此,在我们的例子中,要找出距离增加 10% 导致的价格变化,我们必须计算以下内容:

change_in_price = -294,919.76 * log(1.1)

change_in_price = -294,919.76 * 0.95u003d -28,108.85

根据上述计算,与南湖联盟的距离大约每增加 530 英尺(10% 英里),价格将降低 28,108.85 美元。

如果我们想知道将距离增加 1 英里的效果,我们需要进行以下计算:

change_in_price = -294,919.76 * log(2)u003d -204422.8

附带说明一下,如果我们谈论的是 x 值的小百分比变化(最高 5%),例如 x 增加 5%,几乎相当于在对数中增加 0.05,这将很有帮助(X)。同样,x 增加 2% 几乎相当于在 log(x) 上增加 0.02。