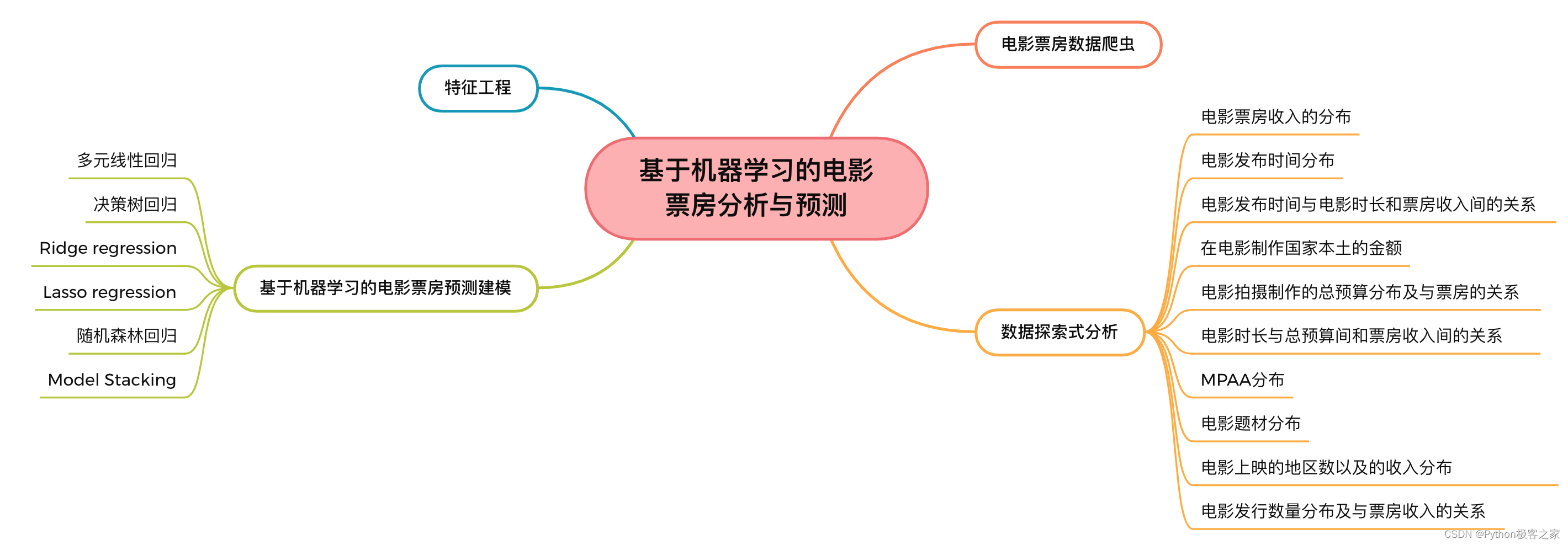
1. 项目简介

票房作为衡量电影能否盈利的重要指标受诸多因素共同作用影响且其影响机制较为复杂，电影票房的准确预测是比较有难度的。本项目利用某开源电影数据集构建票房预测模型，首先将影响电影票房的因素如电影类型、上映档期、导演、演员等量化处理并进行可视化分析。采用多元线性回归模型、决策树回归模型、Ridge
regression 岭回归模型、Lasso regression 岭回归模型和随机森林回归模型实现票房的预测，并进行以上模型的 model
stacking，实现预测误差的进一步降低。

2. 功能组成

3. 电影票房数据集

电影票房数据来自于某公司旗下一个系统性计算电影票房的网站，旨在通过分析、评论、采访和最全面的在线票房追踪这种艺术与商业结合的方式来介绍电影的情况。代码参考上一篇博客
基于python的电影数据爬虫与可视化分析系统：

​
​ # 首页
​ url = ‘https://www.xxxxxx.com/chart/top_lifetime_gross/?area=XWW’
​ # 保存所有的电影信息
​ all_movie_infos = []
​ need_break = False
​
while True:
if need_break:
break

    print('》》》爬取', url)
    headers = {
        'user-agent': util.get_random_user_agent(),
        'accept-language': 'zh-CN,zh;q=0.9',
        'cache-control': 'max-age=0',
        'accept': 'text/html,application/xhtml+xml,application/xml;q=0.9,image/webp,image/apng,*/*;q=0.8'
    }
    response = requests.get(url, headers=headers)
    response.encoding = 'utf8'
    soup = BeautifulSoup(response.text, 'lxml')

    rank_tds = soup.select('td.mojo-field-type-rank')
    movie_tds = soup.select('td.mojo-field-type-title')
    money_tds = soup.select('td.mojo-field-type-money')
    year_tds = soup.select('td.mojo-field-type-year')

    # 下一页
    next_page = soup.find('li', class_='a-last')
    if next_page is None:  # 所有页面爬取完成
        break
    
    try:
        url = 'https://www.xxxxxx.com/' + next_page.a['href']
    except:
        need_break = True
    
    for i in tqdm(range(len(rank_tds))):
        try:
            rank_td, movie_td, money_td, year_td = rank_tds[i], movie_tds[i], money_tds[i], year_tds[i]
            movie_info = {}
            movie_rank = int(rank_td.text.strip())

            movie_name = movie_td.a.text.strip()
            movie_link = 'https://www.boxofficemojo.com/' + movie_td.a['href']
            movie_income = money_td.text.strip()
            movie_income = float(movie_income.replace(',', '')[1:])
            movie_year = int(year_td.text.strip())

            movie_info['movie_name'] = movie_name
            movie_info['movie_link'] = movie_link
            movie_info['movie_income'] = movie_income
            movie_info['movie_year'] = movie_year

            # 电影发行的详细信息
            movie_detail = get_movie_detail(movie_link)
            movie_info.update(movie_detail)
            all_movie_infos.append(movie_info)
        except:
            continue
        
    print('总计爬取 {} 条电影数据'.format(len(all_movie_infos)))

4. 数据探索式分析

抓取的数据如下图所示：

Id| Movie_Name| Movie_Income| Movie_Year| Domestic_Distributor|
Domestic_Opening| Budget| Earliest_Release_Date| MPAA| Running_Time| Genres|
Relase_Areas| Relase_Count
—|—|—|—|—|—|—|—|—|—|—|—|—
0| Avatar| 2.847380e+09| 2009| Twentieth Century Fox| 77025481.0| 237000000.0|
December 16, 2009| PG-13| 162| [Action, Adventure, Fantasy, Sci-Fi]| 6| 83
1| Avengers: Endgame| 2.797501e+09| 2019| Walt Disney Studios Motion Pictures|
357115007.0| 356000000.0| April 24, 2019| PG-13| 181| [Action, Adventure,
Drama, Sci-Fi]| 5| 57
2| Titanic| 2.201647e+09| 1997| Paramount Pictures| 28638131.0| 200000000.0|
December 19, 1997| PG-13| 194| [Drama, Romance]| 6| 78
3| Star Wars: Episode VII - The Force Awakens| 2.069522e+09| 2015| Walt Disney
Studios Motion Pictures| 247966675.0| 245000000.0| December 16, 2015| PG-13|
138| [Action, Adventure, Sci-Fi]| 6| 65
4| Jurassic World| 1.671537e+09| 2015| Universal Pictures| 208806270.0|
150000000.0| June 10, 2015| PG-13| 124| [Action, Adventure, Sci-Fi]| 6| 69

4.1 电影票房收入的分布情况

​
​ plt.figure(figsize=(16, 8))
​ plt.subplot(211)
​ sns.kdeplot(movie_df[‘Movie_Income’])
​ plt.title(‘电影票房收入(美元)的分布情况’, fontsize=16, weight=‘bold’, color=‘black’)
​
plt.subplot(212)
sns.kdeplot(np.log1p(movie_df[‘Movie_Income’]))
plt.title(‘电影票房收入(美元)的分布情况（lop1p转换）’, fontsize=16, weight=‘bold’, color=‘black’)
plt.show()

4.2 电影发布时间分布情况

4.3

电影发布时间与电影时长和票房收入间的关系

​
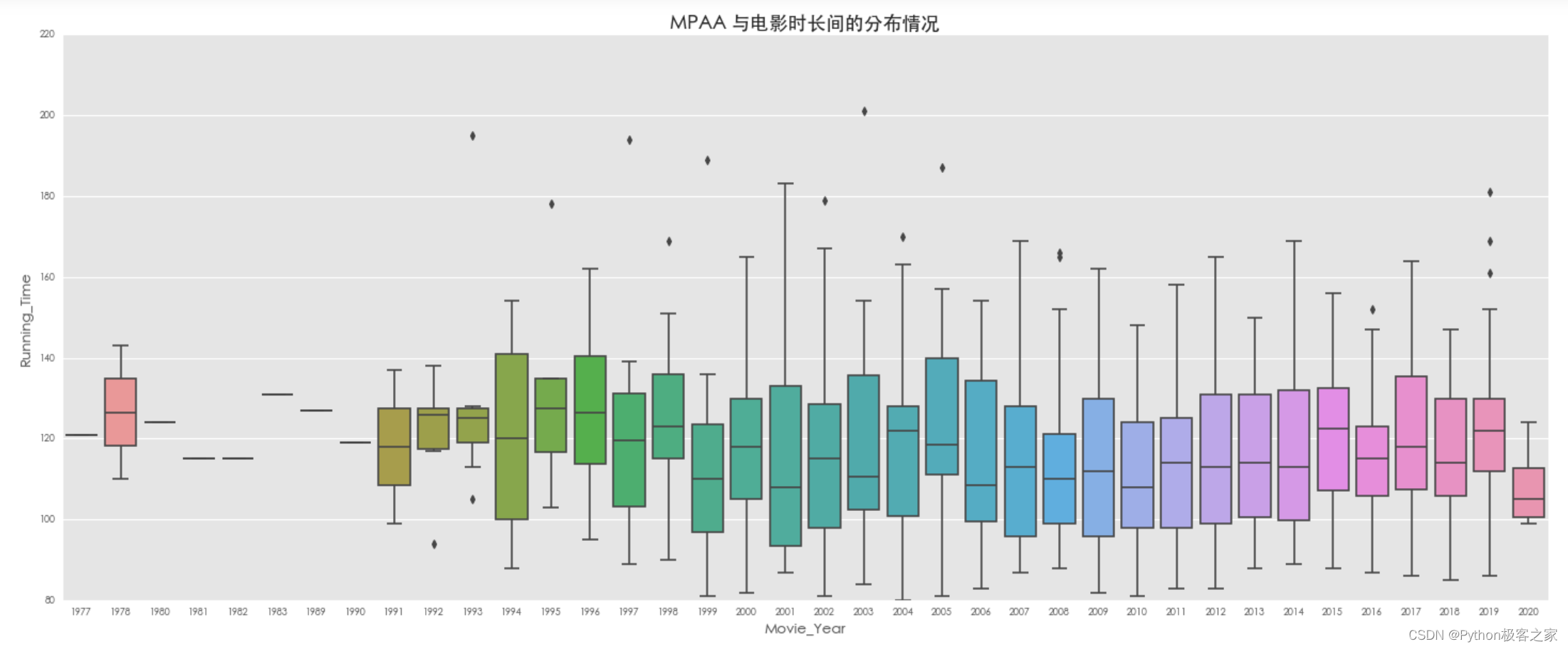
​ plt.figure(figsize=(20, 8))
​ sns.boxplot(x=“Movie_Year”, y=“Running_Time”, data=movie_df, linewidth=1.5)
​ plt.title(‘MPAA 与电影时长间的分布情况’, fontsize=16, weight=‘bold’)
​ plt.show()
​
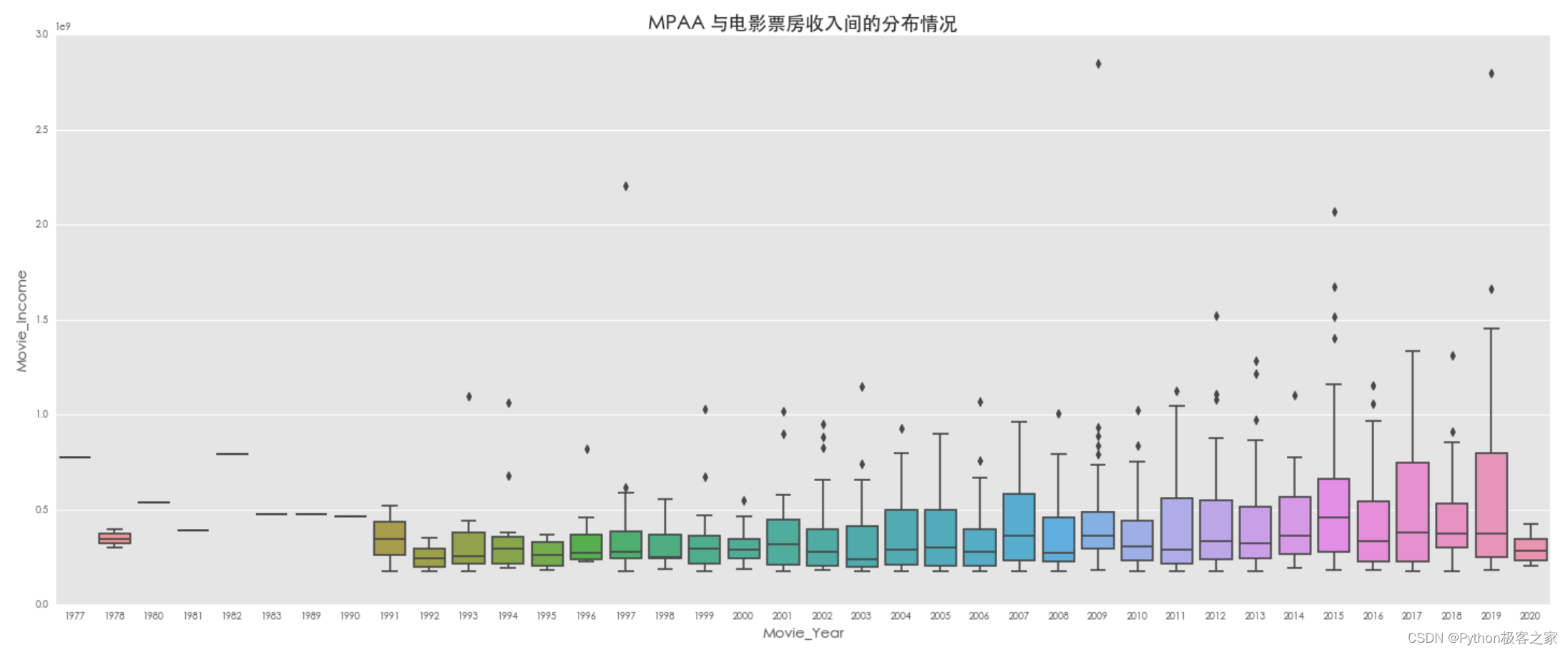
plt.figure(figsize=(20, 8))
sns.boxplot(x=“Movie_Year”, y=“Movie_Income”, data=movie_df, linewidth=1.5)
plt.title(‘MPAA 与电影票房收入间的分布情况’, fontsize=16, weight=‘bold’)
plt.show()

![](https://img-

blog.csdnimg.cn/57af1fce81ed4e5ba67261384cd0fd40.png)![](https://img-
blog.csdnimg.cn/c1afde9928bf4fe6ba06305eb7e02037.png)

4.4 在电影制作国家本土的金额 Domestic Opening

​
​ plt.figure(figsize=(16, 6))
​ plt.subplot(121)
​ sns.distplot(movie_df[‘Domestic_Opening’], kde=True, bins=30)
​ plt.title(‘在电影制作国家本土的金额 Domestic Opening分布情况’, fontsize=16, weight=‘bold’)
​
plt.subplot(122)
plt.scatter(movie_df[‘Domestic_Opening’], movie_df[‘Movie_Income’], s=40, c=‘red’)
plt.title(‘在电影制作国家本土的金额与电影票房收入间的关系’, fontsize=16, weight=‘bold’)
plt.show()

4.5

电影拍摄制作的总预算分布及与票房的关系

4.6 电影时长分布情况

4.7

MPAA分布情况

​
​ plt.figure(figsize=(16, 8))
​ plt.subplot(121)
​ sns.boxplot(x=“MPAA”, y=“Running_Time”, data=movie_df, linewidth=1.5)
​ plt.title(‘MPAA 与电影时长间的分布情况’, fontsize=16, weight=‘bold’)
​
plt.subplot(122)
sns.violinplot(x=“MPAA”, y=“Movie_Income”, data=movie_df, linewidth=1.5)
plt.title(‘MPAA 与电影票房收入间的分布情况’, fontsize=16, weight=‘bold’)
plt.show()

4.8

电影时长与总预算间和票房收入间的关系

​
​ plt.figure(figsize=(16, 6))
​ plt.subplot(121)
​ plt.scatter(movie_df[‘Running_Time’], movie_df[‘Budget’], s=40, c=‘red’)
​ plt.title(‘电影时长与电影制作总预算间的关系’, fontsize=16, weight=‘bold’)
​
plt.subplot(122)
plt.scatter(movie_df[‘Running_Time’], movie_df[‘Movie_Income’], s=40, c=‘blue’)
plt.title(‘电影时长与电影票房收入间的关系’, fontsize=16, weight=‘bold’)
plt.show()

4.9 电影题材分布情况

4.10

电影上映的地区数以及不同地区发行电影的收入分布情况

4.11 电影发行数量分布及与票房收入的关系

5. 特征工程

​
​ …
​
# 电影名称长度
movie_df[‘movie_name_len’] = movie_df[‘Movie_Name’].map(len)
del movie_df[‘Movie_Name’]

# 发行公司名称长度
movie_df['Domestic_Distributor'] = movie_df['Domestic_Distributor'].map(len)

# MPAA 进行编码
tmp = pd.get_dummies(movie_df['MPAA'], prefix='MPAA')
del movie_df['MPAA']
movie_df = pd.concat([movie_df, tmp], axis=1)

# 电影风格数
movie_df['Genres_Count'] = movie_df['Genres'].map(len)

# 电影最早发布的年月日
movie_df['Earliest_Release_Date'] = pd.to_datetime(movie_df['Earliest_Release_Date'])
movie_df['Earliest_Release_Month'] = movie_df['Earliest_Release_Date'].dt.month
movie_df['Earliest_Release_Day'] = movie_df['Earliest_Release_Date'].dt.day
del movie_df['Earliest_Release_Date']

# 电影风格拆分并计算平均票房
all_genres = set(all_genres)

generes_mean_income = {}
generes_mean_budget = {}
generes_mean_dome_opening = {}

for genre in all_genres:
    movie_df['has_cur_genre'] = movie_df['Genres'].map(lambda x: genre in x)
    tmp = movie_df[movie_df['has_cur_genre'] == True]
    generes_mean_income[genre] = np.mean(tmp['Movie_Income'])
    generes_mean_budget[genre] = np.mean(tmp['Budget'])
    generes_mean_dome_opening[genre] = np.mean(tmp['Domestic_Opening'])
    
    del movie_df['has_cur_genre']

......

​
​ # 标签经过 log1p 转换，使其更偏向于正态分布
​ movie_df[‘Movie_Income’] = np.log1p(movie_df[‘Movie_Income’])

6. 基于机器学习的电影票房预测建模

6.1 多元线性回归模型

​
​ kf = KFold(n_splits=roof_flod, shuffle=True, random_state=42)
​
pred_train_full_lr = np.zeros(train_all_x.shape[0])
pred_test_full_lr = 0
cv_scores = []

for i, (train_index, val_index) in enumerate(kf.split(train_all_x, train_all_y)):
    print('==> perform fold {}, train size: {}, validate size: {}'.format(i, len(train_index), len(val_index)))
    train_x, val_x = train_all_x.iloc[train_index, :], train_all_x.iloc[val_index, :]
    train_y, val_y = train_all_y[train_index], train_all_y[val_index]
    
    # 创建多元线性回归模型
    model = LinearRegression()
    model.fit(train_x, train_y)

    # predict train
    predict_train = model.predict(train_x)
    train_rmse = rmse(predict_train, train_y)
    # predict validate
    predict_valid = model.predict(val_x)
    valid_rmse = rmse(predict_valid, val_y)
    # predict test
    predict_test = model.predict(test_x)

    print('train_rmse = {}, valid_rmse = {}'.format(train_rmse, valid_rmse))
    cv_scores.append(valid_rmse)

    # run-out-of-fold predict
    pred_train_full_lr[val_index] = predict_valid
    pred_test_full_lr += predict_test

pred_test_full_lr /= roof_flod
mean_cv_scores = np.mean(cv_scores)
print('Mean cv RMSE:', np.mean(cv_scores), ', Test RMSE:', rmse(pred_test_full_lr, test_y))

K-折交叉训练预测输出：

​
​ ==> perform fold 0, train size: 562, validate size: 94
​ train_rmse = 0.31862885101313665, valid_rmse = 0.3098791941859062
​ ==> perform fold 1, train size: 562, validate size: 94
​ train_rmse = 0.30966531140257375, valid_rmse = 0.3617336453943085
​ ==> perform fold 2, train size: 562, validate size: 94
​ train_rmse = 0.31222553812845333, valid_rmse = 0.3563091301166142
​ ==> perform fold 3, train size: 562, validate size: 94
​ train_rmse = 0.3181045185632806, valid_rmse = 0.313318247756848
​ ==> perform fold 4, train size: 562, validate size: 94
​ train_rmse = 0.3186420846670385, valid_rmse = 0.3104935128466852
​ ==> perform fold 5, train size: 563, validate size: 93
​ train_rmse = 0.31872607444323064, valid_rmse = 0.310674378337045
​ ==> perform fold 6, train size: 563, validate size: 93
​ train_rmse = 0.3148508986101748, valid_rmse = 0.33448099584496277
​ Mean cv RMSE: 0.3281270149260528 , Test RMSE: 0.32021879961540917

6.2 决策树回归模型

​
​ kf = KFold(n_splits=roof_flod, shuffle=True, random_state=42)
​
pred_train_full_gbr = np.zeros(train_all_x.shape[0])
pred_test_full_gbr = 0
cv_scores = []

for i, (train_index, val_index) in enumerate(kf.split(train_all_x, train_all_y)):
    print('==> perform fold {}, train size: {}, validate size: {}'.format(i, len(train_index), len(val_index)))
    train_x, val_x = train_all_x.iloc[train_index, :], train_all_x.iloc[val_index, :]
    train_y, val_y = train_all_y[train_index], train_all_y[val_index]
    
    # 创建决策树回归模型
    model = GradientBoostingRegressor()
    model.fit(train_x, train_y)

    # predict train
    predict_train = model.predict(train_x)
    train_rmse = rmse(predict_train, train_y)
    # predict validate
    predict_valid = model.predict(val_x)
    valid_rmse = rmse(predict_valid, val_y)
    # predict test
    predict_test = model.predict(test_x)

    print('train_rmse = {}, valid_rmse = {}'.format(train_rmse, valid_rmse))
    cv_scores.append(valid_rmse)

    # run-out-of-fold predict
    pred_train_full_gbr[val_index] = predict_valid
    pred_test_full_gbr += predict_test

pred_test_full_gbr /= roof_flod
mean_cv_scores = np.mean(cv_scores)
print('Mean cv RMSE:', np.mean(cv_scores), ', Test RMSE:', rmse(pred_test_full_gbr, test_y))

​
​
​ ==> perform fold 0, train size: 562, validate size: 94
​ train_rmse = 0.16585341237735576, valid_rmse = 0.2743161344954678
​ ==> perform fold 1, train size: 562, validate size: 94
​ train_rmse = 0.16256029394790603, valid_rmse = 0.33622091169682994
​ ==> perform fold 2, train size: 562, validate size: 94
​ train_rmse = 0.16698264461675588, valid_rmse = 0.31826380483528854
​ ==> perform fold 3, train size: 562, validate size: 94
​ train_rmse = 0.16714657472381128, valid_rmse = 0.2492765925230781
​ ==> perform fold 4, train size: 562, validate size: 94
​ train_rmse = 0.16565323847833424, valid_rmse = 0.28515987936616316
​ ==> perform fold 5, train size: 563, validate size: 93
​ train_rmse = 0.16331988438567363, valid_rmse = 0.25909878194635483
​ ==> perform fold 6, train size: 563, validate size: 93
​ train_rmse = 0.16476483231297176, valid_rmse = 0.27423483192336967
​ Mean cv RMSE: 0.28522441954093597 , Test RMSE: 0.30643163298244686

6.3 其他模型

其他模型（Ridge regression 、Lasso regression、随机森林回归）也采用 K-折模式进行训练，此处省略篇幅。

6.4 模型融合 Model Stacking !

​
​ # 维度变换
​ pred_train_full_lr = np.reshape(pred_train_full_lr, (pred_train_full_lr.shape[0], 1))
​ pred_train_full_gbr = np.reshape(pred_train_full_gbr, (pred_train_full_gbr.shape[0], 1))
​ pred_train_full_ridge = np.reshape(pred_train_full_ridge, (pred_train_full_ridge.shape[0], 1))
​ pred_train_full_lasso = np.reshape(pred_train_full_lasso, (pred_train_full_lasso.shape[0], 1))
​ pred_train_full_rf = np.reshape(pred_train_full_rf, (pred_train_full_rf.shape[0], 1))
​
pred_test_full_lr = np.reshape(pred_test_full_lr, (pred_test_full_lr.shape[0], 1))
pred_test_full_gbr = np.reshape(pred_test_full_gbr, (pred_test_full_gbr.shape[0], 1))
pred_test_full_ridge = np.reshape(pred_test_full_ridge, (pred_test_full_ridge.shape[0], 1))
pred_test_full_lasso = np.reshape(pred_test_full_lasso, (pred_test_full_lasso.shape[0], 1))
pred_test_full_rf = np.reshape(pred_test_full_rf, (pred_test_full_rf.shape[0], 1))

# 交叉方式预测的结果进行拼接
oof_train_x = np.concatenate([pred_train_full_lr, pred_train_full_gbr, pred_train_full_ridge,
                              pred_train_full_lasso, pred_train_full_rf], axis=1)

oof_test_x = np.concatenate([pred_test_full_lr, pred_test_full_gbr, pred_test_full_ridge,
                             pred_test_full_lasso, pred_test_full_rf], axis=1)

run-out-of-fold 模式预测的结果作为第二层的特征，再次训练随机森林以实现多模型的融合：

​
​ model = RandomForestRegressor(n_estimators=100, random_state=42,
​ verbose=1, min_samples_split=2,
​ max_depth=32)
​ model.fit(oof_train_x, train_all_y)
​
# 测试集预测
predict_test = model.predict(oof_test_x)
test_rmse = rmse(predict_test, test_y)
print(‘Final Test RMSE:’, test_rmse)

​
​ Final Test RMSE: 0.2934230855349363

6.5 模型性能对比

​
​ fig, ax = plt.subplots(figsize=(8, 4), dpi=100)
​
x = [‘线性回归’, ‘决策树回归’, ‘Ridge 回归’, ‘Lasso回归’, ‘随机森林回归’, ‘模型融合’]
y = [rmse(pred_test_full_lr[:, 0], test_y),
rmse(pred_test_full_gbr[:, 0], test_y),
rmse(pred_test_full_ridge[:, 0], test_y),
rmse(pred_test_full_lasso[:, 0], test_y),
rmse(pred_test_full_rf[:, 0], test_y),
rmse(predict_test, test_y)]

plt.bar(x, y, color='#642EFE')

for a,b,i in zip(x,y,range(len(x))): # zip 函数
    plt.text(a,b+0.01,"%.4f"%y[i],ha='center',fontsize=10) # plt.text 函数

plt.title('机器学习电影票房预测性能对比')
plt.ylim(0.2, 0.35)
fig.tight_layout()
plt.ylabel('rmse')
plt.xlabel('model')
plt.show()

可以看出，结果模型融合 Stacking 后，测试集 RMSE 进一步降低！

项目分享

项目分享：

https://gitee.com/asoonis/feed-neo