大模型技术深入浅出--Attention
本文详解了Transformer中的注意力机制,包括三个核心部分:1)缩放点积注意力公式的运算步骤:相似度匹配、缩放、归一化和加权求和;2)Q、K、V向量的生成方式,通过输入X的线性变换获得;3)自回归生成过程中因果掩码和KV缓存的应用,以两步生成过程为例展示了注意力计算过程,并说明KV缓存如何优化推理效率。整个过程体现了Transformer如何动态计算注意力权重并有效利用历史信息。
1. 注意力公式详解:Attention(Q,K,V)
Transformer 中使用的注意力机制是 缩放点积注意力 (Scaled Dot-Product Attention)。它的公式是:
步骤分解与作用:
|
步骤 |
公式部分 |
作用 |
结果 |
|
相似度匹配 |
|
计算 Q 与所有 K 之间的相似度(点积)。 这决定了每个查询(Q)对序列中所有键(K)的关注程度。 |
注意力分数(Logits) |
|
缩放 |
|
将分数除以 K 向量维度 dk 的平方根。 作用是防止 Q 和 K 的点积过大,使 Softmax 函数的输入落在稳定梯度区间,避免梯度消失。 |
缩放后的注意力分数 |
|
归一化 |
softmax(…) |
将分数转换为概率分布,确保所有注意力权重之和为 1。 这些权重指示了模型应该“听取”每个 V 向量的多少信息。 |
注意力权重(Attention Weights) |
|
加权求和 |
(…)V |
用注意力权重对所有 V 向量进行加权求和。 权重高的 V 向量信息被更多地保留到输出中。 |
最终的注意力输出(上下文向量) |
2. Q,K,V 向量如何获得?
Q(Query)、K(Key)、V(Value)向量都是从同一输入 X(即上一个 Transformer 层的输出或初始嵌入)通过线性变换(即全连接层)获得的。
对于每一个注意力头(head):
-
输入:上层输出的特征矩阵 X(维度:[序列长度×模型维度])。
-
线性投影:模型学习了三个独立的权重矩阵
,
,
。
*
*
*
-
结果:Q,K,V 都是新的矩阵(维度:[序列长度×头维度])。这三个矩阵被用于上面的注意力计算公式。
关键点:这三个权重矩阵 ,
,
是可学习的参数,它们在训练过程中不断优化,从而教会模型如何为不同的任务“查询”信息 (Q),以及如何“索引”和“提供”信息 (K 和 V)。
3. 自回归生成中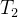 对
对 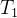 和
和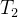 的注意力计算
的注意力计算
我们以一个简单的两步生成过程为例,展示在 Transformer 解码器中(如 ChatGPT),因果掩码和 KV Cache 是如何工作的。
假设输入序列是, 模型已经生成了
, 现在正在生成
。
场景:模型生成 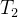
在生成 这一步,模型的输入(到注意力层)是
和
的嵌入。我们将它们简记为
。
1. 计算 Q,K,V
模型计算 T_1 和 T_2 的 Q,K,V 向量:
2. 计算注意力分数 QK^T (应用因果掩码)
计算 Q 矩阵与 K 矩阵的转置的点积:
这得到了一个 2×2 的分数矩阵:
|
Score |
Attention to K1 |
Attention to K2 |
|
Query |
|
|
|
Query |
|
|
应用因果掩码 (Causal Mask):
因果掩码会屏蔽未来的信息。 是第一个 token, 它不能看到
(即未来的
)。 因此, 我们强制将
对
的分数设为
:
3. Softmax 归一化
应用 Softmax 后,所有 的项都会变成 0:
* 是
对自己的注意力权重。
* 是
对
的注意力权重。
* 是
对
的自注意力权重。
4. 加权求和得到输出
计算 Weights⋅V 得到最终输出 :
最终, 的输出
就是对
和
的V 向量进行加权求和的结果。
结合 KV Cache 的优化(推理时)
在实际推理时,为了避免重复计算 的
和
,模型会使用 KV Cache:
-
第一步 (
):计算
,
,并将其存入缓存。
-
第二步 (
):
-
模型只计算新 token
的
,
,
。
-
它从 KV Cache 中取出
] 和
。
-
完整的 K 矩阵用于注意力计算是
。
-
完整的 V 矩阵用于加权求和是
。
-
Q 矩阵只需要
(因为
已经算完,无需再次关注)。
-
模型只需要计算 对
的注意力,避免了重新计算
,
和
的浪费。
因此, 对
和
的注意力是通过
向量与缓存中的
和新计算的
进行相似度匹配, 然后用得到的权重对缓存中的
和新计算的
进行加权求和而获得的。
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容









所有评论(0)