0. 前言

强化学习作为人工智能领域的重要分支，近年来在机器人操作、游戏AI、自动驾驶等领域取得了突破性进展。特别是在机器人操作领域，从传统的仿真训练到真实世界的直接学习，强化学习技术正在经历着革命性的变革。本文将从基础理论出发，深入探讨强化学习的最新发展，特别是SERL系列框架在真实世界机器人操作中的应用。

在现实世界里，要实现高性能的操作并达到高可靠性，对于每一个环境来说，最通用、最具扩展性的办法必然是强化学习。而且它并非是一种被动的数据学习，不是简单地去收集一些离线数据就可以了。如果想要达到100%的可靠性，那就一定要与环境进行交互，而要实现与环境交互，就必须得运用强化学习。

那真机强化学习有什么好处呢？基于生存在物理世界中要比创建一个物理世界更容易的观点。其实我们所处的世界本身就是world model，直接依赖这个world model开始强化学习，绕过仿真sim2real gap和各种物理属性难以仿真等问题。

1. 引言

强化学习（Reinforcement Learning, RL）是人工智能（AI）和机器学习（ML）领域的一个重要子领域，与监督学习和无监督学习并列。它模仿了生物体通过与环境交互来学习最优行为的过程。与传统的监督学习不同，强化学习没有事先标记好的数据集来训练模型。相反，它依靠智能体（Agent）通过不断尝试、失败、适应和优化来学习如何在给定环境中实现特定目标。

强化学习的核心思想来源于心理学中的行为主义理论，即智能体通过试错过程学习最优行为策略。这种学习方式特别适合于解决序列决策问题，其中每个决策都会影响未来的状态和奖励。在机器人操作、游戏AI、金融交易、资源调度等复杂决策场景中，强化学习展现出了强大的学习能力和适应性。

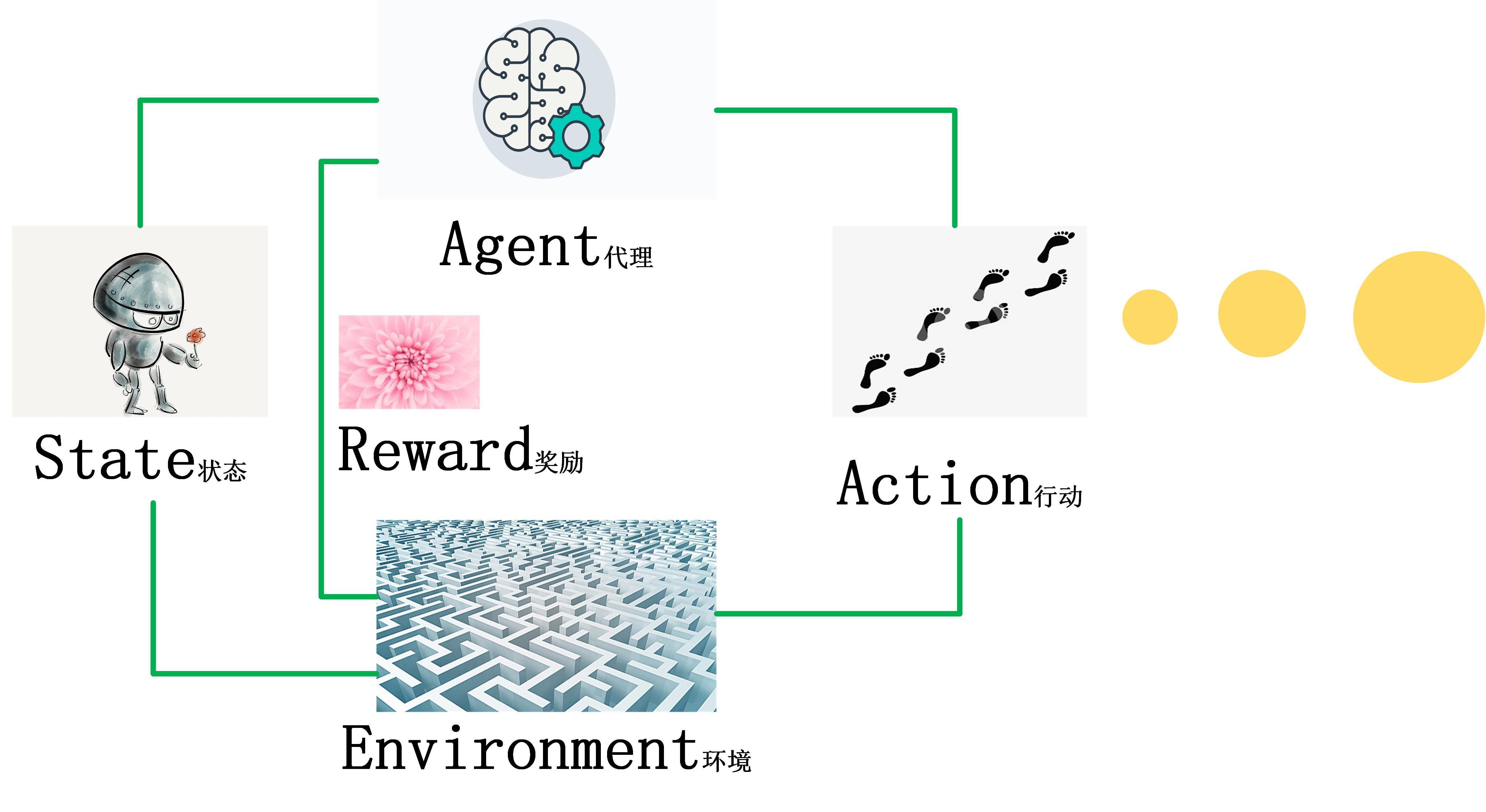
1.1 强化学习的核心组成

强化学习的框架主要由以下几个核心组成：

• 状态（State）：反映环境或系统当前的情况。
• 动作（Action）：智能体在特定状态下可以采取的操作。
• 奖励（Reward）：一个数值反馈，用于量化智能体采取某一动作后环境的反应。
• 策略（Policy）：一个映射函数，指导智能体在特定状态下应采取哪一动作。
  

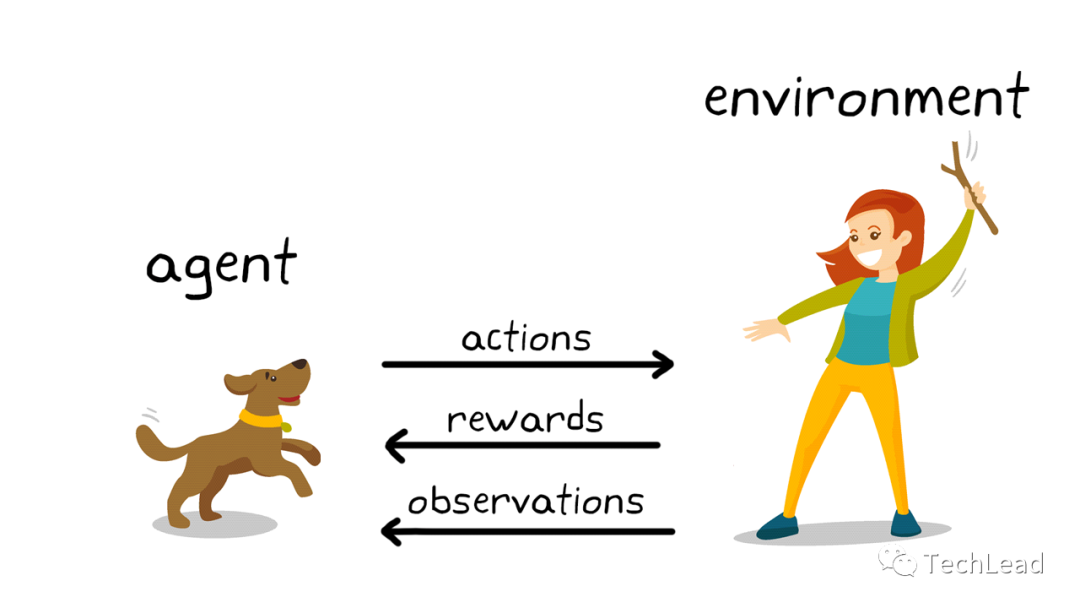
这四个元素共同构成了马尔可夫决策过程（Markov Decision Process, MDP），这是强化学习最核心的数学模型。

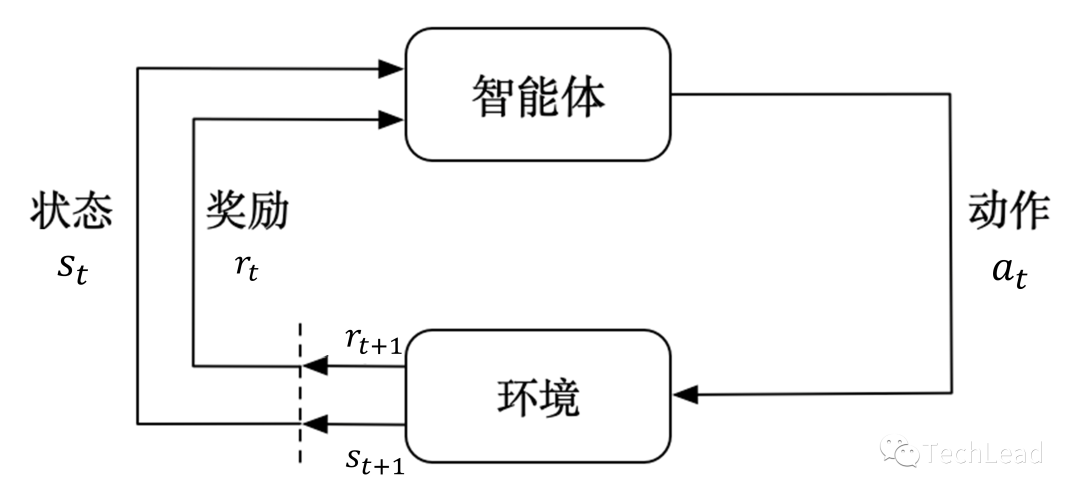
2. 强化学习基础

强化学习的核心是建模决策问题，并通过与环境的交互来学习最佳决策方案。这一过程常常是通过马尔可夫决策过程（Markov Decision Process, MDP）来描述和解决的。在本节中，我们将详细地探讨马尔可夫决策过程以及其核心组件：奖励、状态、动作和策略。

2.1 马尔可夫决策过程（MDP）

MDP是用来描述决策问题的数学模型，主要由一个五元组 (S, A, P, R, γ) 组成。

• 状态空间（S）：表示所有可能状态的集合。在机器人操作中，状态可能包括机器人的关节角度、末端执行器位置、视觉观测等信息。
• 动作空间（A）：表示在特定状态下可能采取的所有动作的集合。对于机械臂，动作通常是关节角度或末端执行器的位移。
• 状态转移概率（P）：P(s’|s, a) 表示在状态 s 下采取动作 a 转移到状态 s’ 的概率。这个概率函数描述了环境的动态特性。
• 奖励函数（R）：R(s, a) 表示在状态 s 下采取动作 a 后获得的即时奖励。奖励函数的设计对强化学习的效果至关重要。
• 折扣因子（γ）：用于权衡当前奖励与未来奖励的重要性，取值范围为 [0,1]。γ接近1时更重视长期奖励，接近0时更重视即时奖励。
  

2.1.1 MDP的数学表示

强化学习的目标是找到一个最优策略π*，使得期望累积奖励最大化：

$$J(\pi )={\mathbb{E}}_{\tau \sim \pi }\left[\sum _{t=0}^T{\gamma }^{t}R(s_t,a_t)\right]$$

其中τ表示轨迹，T是时间步长。最优策略满足：

$${\pi }^{\ast }=\arg \underset{\pi }{\max }J(\pi )$$

2.1.2 状态（State）

在MDP中，状态是用来描述环境或问题的现状。在不同应用中，状态可以有很多种表现形式：

• 在棋类游戏中，状态通常表示棋盘上各个棋子的位置。
• 在自动驾驶中，状态可能包括车辆的速度、位置、以及周围对象的状态等。

2.1.3 动作（Action）

动作是智能体（Agent）在某一状态下可以采取的操作。动作会影响环境，并可能导致状态的转变。

• 在股市交易中，动作通常是"买入"、“卖出"或"持有”。
• 在游戏如"超级马里奥"中，动作可能包括"跳跃"、"下蹲"或"向前移动"等。

2.1.4 奖励（Reward）

奖励是一个数值反馈，用于评估智能体采取某一动作的"好坏"。通常，智能体的目标是最大化累积奖励。

• 在迷宫问题中，到达目的地可能会得到正奖励，而撞到墙壁则可能会得到负奖励。

2.1.5 策略（Policy）

策略是一个从状态到动作的映射函数，用于指导智能体在每一状态下应采取哪一动作。形式上，策略通常表示为 π(a|s)，代表在状态 s 下采取动作 a 的概率。

• 在游戏如"五子棋"中，策略可能是一个复杂的神经网络，用于评估每一步棋的优劣。

通过优化策略，我们可以使智能体在与环境的交互中获得更高的累积奖励，从而实现更优的性能。

3. 常用强化学习算法

强化学习拥有多种算法，用于解决不同类型的问题。在本节中，我们将探讨几种常用的强化学习算法，包括他们的工作原理、意义以及应用实例。这些算法构成了强化学习领域的核心工具箱，每种算法都有其独特的优势和适用场景。

3.1 值迭代（Value Iteration）

3.1.1 算法描述

值迭代是一种基于动态规划（Dynamic Programming）的方法，用于计算最优策略。主要思想是通过迭代更新状态值函数（Value Function）来找到最优策略。该算法通过不断改进对每个状态价值的估计，最终收敛到最优值函数。

值迭代的核心更新公式为：

$$V_{k+1}(s)=\underset{a}{\max }\sum _{s^{\prime }}P(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma V_k(s^{\prime })]$$

其中：

• $V_k(s)$ 是第k次迭代时状态s的值函数
• $P(s^{\prime }|s,a)$ 是状态转移概率
• $R(s,a,s^{\prime })$ 是奖励函数
• $\gamma$ 是折扣因子

3.1.2 算法意义

值迭代算法主要用于解决具有完全可观测状态和已知转移概率的MDP问题。它是一种"模型已知"的算法，要求智能体完全了解环境的动态特性。这种算法具有理论保证，能够收敛到最优策略，但计算复杂度较高。

3.1.3 应用实例

值迭代经常用于路径规划、游戏（如迷宫问题）等环境中，其中所有状态和转移概率都是已知的。在机器人导航中，值迭代可以帮助机器人找到从起点到终点的最优路径。

import numpy as np

def value_iteration(env, gamma=0.9, theta=1e-6):
    """
    值迭代算法实现
    """
    V = np.zeros(env.nS)  # 初始化值函数
    
    while True:
        delta = 0
        for s in range(env.nS):
            v = V[s]
            # 计算所有可能动作的值
            action_values = []
            for a in range(env.nA):
                action_value = 0
                for prob, next_state, reward, done in env.P[s][a]:
                    action_value += prob * (reward + gamma * V[next_state])
                action_values.append(action_value)
            
            V[s] = max(action_values)  # 选择最大价值
            delta = max(delta, abs(v - V[s]))
        
        if delta < theta:
            break
    
    # 提取最优策略
    policy = np.zeros([env.nS, env.nA])
    for s in range(env.nS):
        action_values = []
        for a in range(env.nA):
            action_value = 0
            for prob, next_state, reward, done in env.P[s][a]:
                action_value += prob * (reward + gamma * V[next_state])
            action_values.append(action_value)
        best_action = np.argmax(action_values)
        policy[s, best_action] = 1.0
    
    return policy, V

3.2 Q学习（Q-Learning）

3.2.1 算法描述

Q学习是一种基于值函数的"模型无知"算法。它通过更新Q值（状态-动作值函数）来找到最优策略。Q学习是强化学习中最经典的算法之一，具有简单、有效、收敛性好的特点。

Q学习的核心更新公式为：

$$Q(s,a)\leftarrow Q(s,a)+\alpha [r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })-Q(s,a)]$$

其中：

• $Q(s,a)$ 是状态-动作值函数
• $\alpha$ 是学习率
• $r$ 是即时奖励
• $\gamma$ 是折扣因子
• $s^{\prime }$ 是下一个状态

3.2.2 算法意义

Q学习算法适用于"模型无知"的场景，也就是说，智能体并不需要知道环境的完整信息。因此，Q学习特别适用于现实世界的问题。该算法具有以下优势：

1. 无模型学习：不需要环境模型，只需要与环境交互
2. 在线学习：可以在与环境交互的过程中实时学习
3. 收敛保证：在满足一定条件下，Q学习能够收敛到最优策略
4. 简单实现：算法逻辑简单，易于实现和调试

3.2.3 应用实例

Q学习广泛用于机器人导航、电子商务推荐系统以及多玩家游戏等。在机器人导航中，Q学习可以帮助机器人学习在不同环境下选择最优的移动策略。

import numpy as np
import random

class QLearning:
    def __init__(self, state_size, action_size, learning_rate=0.1, 
                 discount_factor=0.95, epsilon=0.1):
        self.state_size = state_size
        self.action_size = action_size
        self.learning_rate = learning_rate
        self.discount_factor = discount_factor
        self.epsilon = epsilon
        
        # 初始化Q表
        self.q_table = np.zeros((state_size, action_size))
    
    def choose_action(self, state, training=True):
        """
        选择动作：epsilon-贪婪策略
        """
        if training and random.random() < self.epsilon:
            return random.choice(range(self.action_size))
        else:
            return np.argmax(self.q_table[state])
    
    def update(self, state, action, reward, next_state, done):
        """
        更新Q值
        """
        current_q = self.q_table[state, action]
        if done:
            target_q = reward
        else:
            target_q = reward + self.discount_factor * np.max(self.q_table[next_state])
        
        self.q_table[state, action] += self.learning_rate * (target_q - current_q)
    
    def decay_epsilon(self, decay_rate=0.995):
        """
        衰减探索率
        """
        self.epsilon = max(0.01, self.epsilon * decay_rate)

3.3 策略梯度（Policy Gradients）

3.3.1 算法描述

与基于值函数的方法不同，策略梯度方法直接在策略空间中进行优化。算法通过计算梯度来更新策略参数。策略梯度方法的核心思想是直接优化策略函数，而不是通过值函数间接优化。

策略梯度的核心公式为：

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[\sum _{t=0}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)A_t\right]$$

其中：

• $J(\theta )$ 是策略的目标函数
• ${\pi }_{\theta }(a_t|s_t)$ 是策略函数
• $A_t$ 是优势函数
• $\tau$ 是轨迹

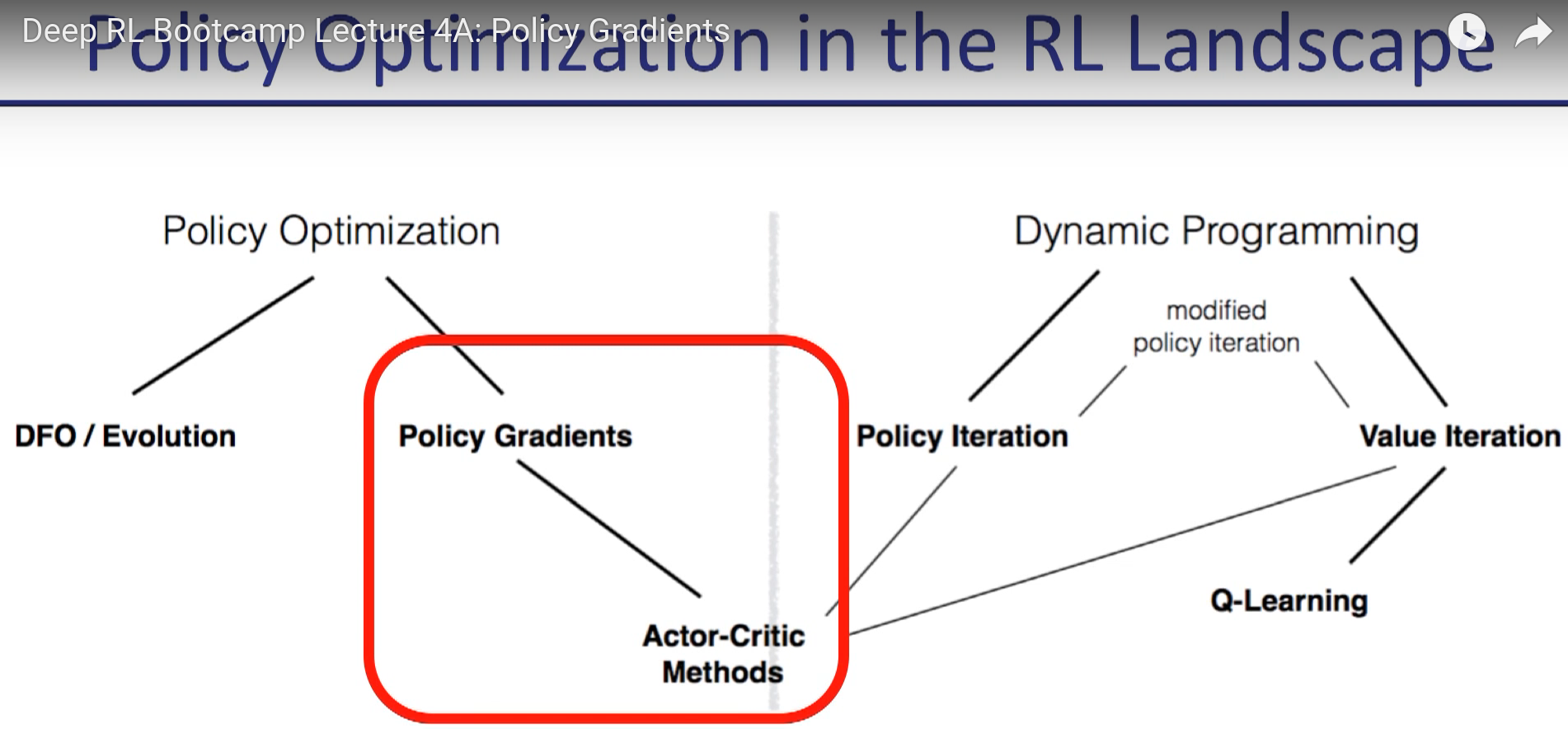
3.3.2 算法意义

策略梯度方法特别适用于处理高维或连续的动作和状态空间，而这些在基于值的方法中通常很难处理。该方法的优势包括：

1. 连续动作空间：能够处理连续的动作空间，如机器人控制
2. 随机策略：可以学习随机策略，增加探索性
3. 端到端学习：直接从状态到动作的映射，无需中间值函数
4. 理论保证：具有收敛性理论保证

3.3.3 应用实例

策略梯度方法在自然语言处理（如机器翻译）、连续控制问题（如机器人手臂控制）等方面有广泛应用。在机器人控制中，策略梯度可以帮助机器人学习复杂的运动技能。

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical

class PolicyNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=128):
        super(PolicyNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, action_dim)
    
    def forward(self, state):
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        action_probs = F.softmax(self.fc3(x), dim=-1)
        return action_probs

class PolicyGradient:
    def __init__(self, state_dim, action_dim, learning_rate=1e-3):
        self.policy_net = PolicyNetwork(state_dim, action_dim)
        self.optimizer = optim.Adam(self.policy_net.parameters(), lr=learning_rate)
        
    def select_action(self, state):
        """
        选择动作
        """
        state = torch.FloatTensor(state).unsqueeze(0)
        action_probs = self.policy_net(state)
        dist = Categorical(action_probs)
        action = dist.sample()
        log_prob = dist.log_prob(action)
        return action.item(), log_prob
    
    def update_policy(self, rewards, log_probs):
        """
        更新策略
        """
        # 计算折扣奖励
        discounted_rewards = []
        running_reward = 0
        for reward in reversed(rewards):
            running_reward = reward + 0.99 * running_reward
            discounted_rewards.insert(0, running_reward)
        
        # 标准化奖励
        discounted_rewards = torch.FloatTensor(discounted_rewards)
        discounted_rewards = (discounted_rewards - discounted_rewards.mean()) / (discounted_rewards.std() + 1e-8)
        
        # 计算策略损失
        policy_loss = []
        for log_prob, reward in zip(log_probs, discounted_rewards):
            policy_loss.append(-log_prob * reward)
        
        # 更新网络
        self.optimizer.zero_grad()
        policy_loss = torch.cat(policy_loss).sum()
        policy_loss.backward()
        self.optimizer.step()

3.4 演员-评论家（Actor-Critic）

3.4.1 算法描述

Actor-Critic 结合了值函数方法和策略梯度方法的优点。其中，“Actor” 负责决策，“Critic” 负责评价这些决策。这种架构能够同时学习策略和价值函数，实现更稳定和高效的学习。

Actor-Critic的核心思想是：

• Actor（演员）：学习策略函数 $\pi (a|s)$，负责选择动作
• Critic（评论家）：学习价值函数 $V(s)$ 或 $Q(s,a)$，负责评估状态或动作的价值

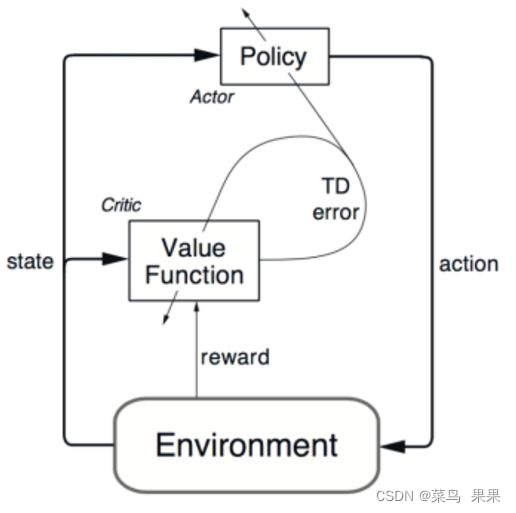
Actor-Critic的更新公式为：

$${\theta }_{t+1}={\theta }_t+\alpha {\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)A_t$$

$$w_{t+1}=w_t+\beta {\nabla }_w(R_{t+1}+\gamma V_w(s_{t+1})-V_w(s_t)){\nabla }_w{V}_w(s_t)$$

其中：

• $\theta$ 是Actor的参数
• $w$ 是Critic的参数
• $A_t$ 是优势函数
• $\alpha ,\beta$ 是学习率

3.4.2 算法意义

通过结合值函数和策略优化，Actor-Critic 能在各种不同的环境中实现更快和更稳定的学习。该方法的优势包括：

1. 稳定性：Critic提供稳定的价值估计，减少策略梯度的方差
2. 效率：同时学习策略和价值函数，提高学习效率
3. 在线学习：可以在线更新，无需等待回合结束
4. 灵活性：可以处理连续和离散动作空间

3.4.3 应用实例

在自动驾驶、资源分配和多智能体系统等复杂问题中，Actor-Critic 方法被广泛应用。在自动驾驶中，Actor负责控制车辆，Critic负责评估驾驶行为的安全性。

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

class ActorCritic(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=128):
        super(ActorCritic, self).__init__()
        
        # Actor网络
        self.actor = nn.Sequential(
            nn.Linear(state_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, action_dim),
            nn.Softmax(dim=-1)
        )
        
        # Critic网络
        self.critic = nn.Sequential(
            nn.Linear(state_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, 1)
        )
    
    def forward(self, state):
        action_probs = self.actor(state)
        state_value = self.critic(state)
        return action_probs, state_value

class ActorCriticAgent:
    def __init__(self, state_dim, action_dim, lr_actor=1e-3, lr_critic=1e-3):
        self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
        self.model = ActorCritic(state_dim, action_dim).to(self.device)
        
        self.actor_optimizer = optim.Adam(self.model.actor.parameters(), lr=lr_actor)
        self.critic_optimizer = optim.Adam(self.model.critic.parameters(), lr=lr_critic)
        
    def select_action(self, state):
        """
        选择动作
        """
        state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
        action_probs, state_value = self.model(state)
        
        dist = torch.distributions.Categorical(action_probs)
        action = dist.sample()
        log_prob = dist.log_prob(action)
        
        return action.item(), log_prob, state_value
    
    def update(self, states, actions, rewards, next_states, dones, log_probs, state_values):
        """
        更新Actor和Critic
        """
        states = torch.FloatTensor(states).to(self.device)
        actions = torch.LongTensor(actions).to(self.device)
        rewards = torch.FloatTensor(rewards).to(self.device)
        next_states = torch.FloatTensor(next_states).to(self.device)
        dones = torch.BoolTensor(dones).to(self.device)
        log_probs = torch.stack(log_probs).to(self.device)
        state_values = torch.stack(state_values).squeeze().to(self.device)
        
        # 计算目标价值
        with torch.no_grad():
            _, next_state_values = self.model(next_states)
            targets = rewards + 0.99 * next_state_values.squeeze() * (~dones)
        
        # 计算优势
        advantages = targets - state_values
        
        # 更新Critic
        critic_loss = F.mse_loss(state_values, targets)
        self.critic_optimizer.zero_grad()
        critic_loss.backward(retain_graph=True)
        self.critic_optimizer.step()
        
        # 更新Actor
        actor_loss = -(log_probs * advantages.detach()).mean()
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

3.5 PPO（Proximal Policy Optimization）算法

PPO是一种高效、可靠的强化学习算法，属于策略梯度家族的一部分。由于其高效和稳定的性质，PPO算法在各种强化学习任务中都有广泛的应用。PPO算法通过限制策略更新的幅度，避免了传统策略梯度方法中可能出现的性能崩溃问题。

3.5.1 原理

PPO的核心思想是通过限制策略更新的步长来避免太大的性能下降。这是通过引入一种特殊的目标函数实现的，该目标函数包含一个剪辑（Clipping）项来限制策略的改变程度。

PPO的目标函数为：

$$L^{CLIP}(\theta )={\mathbb{E}}_t\left[\min (r_t(\theta )A_t,\text{clip}(r_t(\theta ),1-ϵ,1+ϵ)A_t)\right]$$

其中：

• $r_t(\theta )=\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{{\theta }_{old}}(a_t|s_t)}$ 是概率比率
• $A_t$ 是优势函数
• $ϵ$ 是剪辑参数（通常为0.2）

PPO算法的关键创新在于：

1. 概率比率裁剪：限制新旧策略之间的差异，防止策略更新过大
2. 保守更新：当优势为正时，限制策略改进的上限；当优势为负时，限制策略恶化的下限
3. 多次更新：对同一批数据可以进行多次更新，提高样本效率

3.5.2 算法细节

PPO算法的实现细节包括：

• 多步优势估计：PPO通常与多步回报（Multi-Step Return）和优势函数（Advantage Function）结合使用，以减少估计误差。优势函数通过GAE（Generalized Advantage Estimation）计算，能够有效减少方差。
• 自适应学习率：PPO通常使用自适应学习率和高级优化器（如Adam），能够自动调整学习步长，提高训练稳定性。
• 并行采样：由于PPO是一种"样本高效"的算法，通常与并行环境采样结合使用，以进一步提高效率。多个环境同时运行可以快速收集大量经验数据。

3.5.3 代码举例

下面是使用Python和PyTorch实现PPO的完整示例：

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import numpy as np

class PPONetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=128):
        super(PPONetwork, self).__init__()
        
        # 共享特征提取层
        self.shared_layers = nn.Sequential(
            nn.Linear(state_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU()
        )
        
        # Actor头：输出动作概率
        self.actor = nn.Linear(hidden_dim, action_dim)
        
        # Critic头：输出状态价值
        self.critic = nn.Linear(hidden_dim, 1)
    
    def forward(self, state):
        features = self.shared_layers(state)
        action_probs = F.softmax(self.actor(features), dim=-1)
        state_value = self.critic(features)
        return action_probs, state_value

class PPOAgent:
    def __init__(self, state_dim, action_dim, lr=3e-4, gamma=0.99, 
                 eps_clip=0.2, k_epochs=4, entropy_coef=0.01):
        self.gamma = gamma
        self.eps_clip = eps_clip
        self.k_epochs = k_epochs
        self.entropy_coef = entropy_coef
        
        self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
        self.policy = PPONetwork(state_dim, action_dim).to(self.device)
        self.optimizer = optim.Adam(self.policy.parameters(), lr=lr)
        
        self.old_policy = PPONetwork(state_dim, action_dim).to(self.device)
        self.old_policy.load_state_dict(self.policy.state_dict())
    
    def select_action(self, state):
        """
        选择动作
        """
        state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
        with torch.no_grad():
            action_probs, state_value = self.old_policy(state)
            dist = Categorical(action_probs)
            action = dist.sample()
            log_prob = dist.log_prob(action)
        
        return action.item(), log_prob.cpu().numpy(), state_value.cpu().numpy()
    
    def update(self, states, actions, rewards, next_states, dones, 
               old_log_probs, old_state_values):
        """
        更新策略
        """
        # 转换为张量
        states = torch.FloatTensor(states).to(self.device)
        actions = torch.LongTensor(actions).to(self.device)
        rewards = torch.FloatTensor(rewards).to(self.device)
        next_states = torch.FloatTensor(next_states).to(self.device)
        dones = torch.BoolTensor(dones).to(self.device)
        old_log_probs = torch.FloatTensor(old_log_probs).to(self.device)
        old_state_values = torch.FloatTensor(old_state_values).to(self.device)
        
        # 计算折扣奖励和优势
        returns = []
        advantages = []
        running_return = 0
        running_advantage = 0
        
        for t in reversed(range(len(rewards))):
            if dones[t]:
                running_return = 0
                running_advantage = 0
            
            running_return = rewards[t] + self.gamma * running_return
            returns.insert(0, running_return)
            
            td_error = rewards[t] + self.gamma * old_state_values[t+1] * (1 - dones[t]) - old_state_values[t]
            running_advantage = td_error + self.gamma * 0.95 * running_advantage * (1 - dones[t])
            advantages.insert(0, running_advantage)
        
        returns = torch.FloatTensor(returns).to(self.device)
        advantages = torch.FloatTensor(advantages).to(self.device)
        advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
        
        # 多次更新
        for _ in range(self.k_epochs):
            # 获取当前策略的输出
            action_probs, state_values = self.policy(states)
            dist = Categorical(action_probs)
            log_probs = dist.log_prob(actions)
            entropy = dist.entropy().mean()
            
            # 计算概率比率
            ratio = torch.exp(log_probs - old_log_probs)
            
            # 计算PPO损失
            surr1 = ratio * advantages
            surr2 = torch.clamp(ratio, 1 - self.eps_clip, 1 + self.eps_clip) * advantages
            actor_loss = -torch.min(surr1, surr2).mean()
            
            # 计算Critic损失
            critic_loss = F.mse_loss(state_values.squeeze(), returns)
            
            # 总损失
            total_loss = actor_loss + 0.5 * critic_loss - self.entropy_coef * entropy
            
            # 更新网络
            self.optimizer.zero_grad()
            total_loss.backward()
            torch.nn.utils.clip_grad_norm_(self.policy.parameters(), 0.5)
            self.optimizer.step()
        
        # 更新旧策略
        self.old_policy.load_state_dict(self.policy.state_dict())

# 使用示例
def train_ppo_agent(env, agent, num_episodes=1000):
    """
    训练PPO智能体
    """
    for episode in range(num_episodes):
        state = env.reset()
        episode_reward = 0
        
        states, actions, rewards, next_states, dones = [], [], [], [], []
        old_log_probs, old_state_values = [], []
        
        for step in range(1000):  # 假设最大步数为1000
            action, log_prob, state_value = agent.select_action(state)
            next_state, reward, done, _ = env.step(action)
            
            states.append(state)
            actions.append(action)
            rewards.append(reward)
            next_states.append(next_state)
            dones.append(done)
            old_log_probs.append(log_prob)
            old_state_values.append(state_value)
            
            state = next_state
            episode_reward += reward
            
            if done:
                break
        
        # 更新策略
        if len(states) > 0:
            agent.update(states, actions, rewards, next_states, dones, 
                        old_log_probs, old_state_values)
        
        if episode % 100 == 0:
            print(f"Episode {episode}, Reward: {episode_reward:.2f}")

print("PPO算法实现完成！")

这个完整的PPO实现包含了所有关键组件：Actor-Critic架构、概率比率裁剪、优势函数计算、多次更新等。实际应用中还需要根据具体任务调整超参数和网络结构。

4. 强化学习实战

强化学习在实际应用中需要考虑多个方面，包括环境设计、模型架构、训练策略、评估方法等。本节将详细介绍如何构建一个完整的强化学习系统。

4.1 模型创建

4.1.1 网络架构设计

在强化学习中，网络架构的设计对性能有重要影响。常见的架构包括：

1. 全连接网络（MLP）
适用于状态空间较小的任务，如经典控制问题。

import torch
import torch.nn as nn
import torch.nn.functional as F

class MLPNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dims, output_dim, activation='relu'):
        super(MLPNetwork, self).__init__()
        
        layers = []
        prev_dim = input_dim
        
        for hidden_dim in hidden_dims:
            layers.append(nn.Linear(prev_dim, hidden_dim))
            if activation == 'relu':
                layers.append(nn.ReLU())
            elif activation == 'tanh':
                layers.append(nn.Tanh())
            elif activation == 'leaky_relu':
                layers.append(nn.LeakyReLU())
            prev_dim = hidden_dim
        
        layers.append(nn.Linear(prev_dim, output_dim))
        self.network = nn.Sequential(*layers)
    
    def forward(self, x):
        return self.network(x)

# 使用示例
state_dim = 4
action_dim = 2
hidden_dims = [128, 128, 64]

# 创建策略网络
policy_net = MLPNetwork(state_dim, hidden_dims, action_dim)
print(f"策略网络参数数量: {sum(p.numel() for p in policy_net.parameters())}")

2. 卷积神经网络（CNN）
适用于图像输入的任务，如Atari游戏。

class CNNNetwork(nn.Module):
    def __init__(self, input_channels, output_dim):
        super(CNNNetwork, self).__init__()
        
        self.conv_layers = nn.Sequential(
            nn.Conv2d(input_channels, 32, kernel_size=8, stride=4),
            nn.ReLU(),
            nn.Conv2d(32, 64, kernel_size=4, stride=2),
            nn.ReLU(),
            nn.Conv2d(64, 64, kernel_size=3, stride=1),
            nn.ReLU()
        )
        
        # 计算卷积层输出尺寸
        self.conv_output_size = self._get_conv_output_size(input_channels)
        
        self.fc_layers = nn.Sequential(
            nn.Linear(self.conv_output_size, 512),
            nn.ReLU(),
            nn.Linear(512, output_dim)
        )
    
    def _get_conv_output_size(self, input_channels):
        # 假设输入图像尺寸为84x84
        dummy_input = torch.zeros(1, input_channels, 84, 84)
        with torch.no_grad():
            conv_output = self.conv_layers(dummy_input)
        return conv_output.view(1, -1).size(1)
    
    def forward(self, x):
        conv_out = self.conv_layers(x)
        conv_out = conv_out.view(conv_out.size(0), -1)
        return self.fc_layers(conv_out)

# 使用示例
input_channels = 4  # 4帧堆叠
action_dim = 6      # Atari游戏的动作数
cnn_net = CNNNetwork(input_channels, action_dim)
print(f"CNN网络参数数量: {sum(p.numel() for p in cnn_net.parameters())}")

3. 循环神经网络（RNN/LSTM）
适用于序列决策任务，如自然语言处理或部分可观测环境。

class RNNNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, num_layers=2):
        super(RNNNetwork, self).__init__()
        
        self.hidden_dim = hidden_dim
        self.num_layers = num_layers
        
        self.lstm = nn.LSTM(input_dim, hidden_dim, num_layers, 
                           batch_first=True, dropout=0.1)
        self.fc = nn.Linear(hidden_dim, output_dim)
    
    def forward(self, x, hidden=None):
        if hidden is None:
            h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim)
            c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim)
            hidden = (h0, c0)
        
        lstm_out, hidden = self.lstm(x, hidden)
        # 取最后一个时间步的输出
        output = self.fc(lstm_out[:, -1, :])
        return output, hidden

# 使用示例
input_dim = 10
hidden_dim = 64
output_dim = 4
seq_length = 20

rnn_net = RNNNetwork(input_dim, hidden_dim, output_dim)
dummy_input = torch.randn(32, seq_length, input_dim)  # batch_size=32
output, hidden = rnn_net(dummy_input)
print(f"RNN网络输出形状: {output.shape}")

4.1.2 模型初始化

正确的权重初始化对训练稳定性至关重要：

def init_weights(m):
    """初始化网络权重"""
    if isinstance(m, nn.Linear):
        # Xavier初始化
        nn.init.xavier_uniform_(m.weight)
        if m.bias is not None:
            nn.init.constant_(m.bias, 0)
    elif isinstance(m, nn.Conv2d):
        # He初始化
        nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
        if m.bias is not None:
            nn.init.constant_(m.bias, 0)
    elif isinstance(m, nn.LSTM):
        for name, param in m.named_parameters():
            if 'weight' in name:
                nn.init.xavier_uniform_(param)
            elif 'bias' in name:
                nn.init.constant_(param, 0)

# 应用权重初始化
policy_net.apply(init_weights)
cnn_net.apply(init_weights)
rnn_net.apply(init_weights)

4.1.3 模型保存与加载

import os
import json

class ModelManager:
    def __init__(self, save_dir):
        self.save_dir = save_dir
        os.makedirs(save_dir, exist_ok=True)
    
    def save_model(self, model, optimizer, epoch, loss, extra_info=None):
        """保存模型"""
        save_path = os.path.join(self.save_dir, f"model_epoch_{epoch}.pth")
        
        save_dict = {
            'model_state_dict': model.state_dict(),
            'optimizer_state_dict': optimizer.state_dict(),
            'epoch': epoch,
            'loss': loss
        }
        
        if extra_info:
            save_dict.update(extra_info)
        
        torch.save(save_dict, save_path)
        print(f"模型已保存到: {save_path}")
    
    def load_model(self, model, optimizer, epoch):
        """加载模型"""
        load_path = os.path.join(self.save_dir, f"model_epoch_{epoch}.pth")
        
        if not os.path.exists(load_path):
            print(f"模型文件不存在: {load_path}")
            return None
        
        checkpoint = torch.load(load_path)
        model.load_state_dict(checkpoint['model_state_dict'])
        optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
        
        print(f"模型已从 {load_path} 加载")
        return checkpoint
    
    def save_config(self, config):
        """保存配置"""
        config_path = os.path.join(self.save_dir, "config.json")
        with open(config_path, 'w') as f:
            json.dump(config, f, indent=2)
        print(f"配置已保存到: {config_path}")

# 使用示例
model_manager = ModelManager("./models")
config = {
    "state_dim": 4,
    "action_dim": 2,
    "learning_rate": 1e-3,
    "batch_size": 64,
    "gamma": 0.99
}
model_manager.save_config(config)

4.2 训练流程

4.2.1 环境设置

在强化学习实战中，环境设置是第一步也是至关重要的一步。通常，这一阶段包括环境初始化、状态空间定义、动作空间定义等。

import gym
import numpy as np
from gym import spaces
import matplotlib.pyplot as plt

class CustomEnvironment:
    """自定义环境示例"""
    def __init__(self):
        # 状态空间：4维连续状态
        self.observation_space = spaces.Box(
            low=-np.inf, high=np.inf, shape=(4,), dtype=np.float32
        )
        # 动作空间：2个离散动作
        self.action_space = spaces.Discrete(2)
        
        self.state = None
        self.max_steps = 200
        self.current_step = 0
    
    def reset(self):
        """重置环境"""
        self.state = np.random.uniform(-0.1, 0.1, 4)
        self.current_step = 0
        return self.state.copy()
    
    def step(self, action):
        """执行动作"""
        self.current_step += 1
        
        # 简化的动力学模型
        if action == 0:  # 向左
            self.state[0] += 0.1
        else:  # 向右
            self.state[0] -= 0.1
        
        # 计算奖励
        reward = 1.0 if abs(self.state[0]) < 0.5 else -1.0
        
        # 判断是否结束
        done = (self.current_step >= self.max_steps or 
                abs(self.state[0]) > 2.0)
        
        return self.state.copy(), reward, done, {}
    
    def render(self):
        """可视化环境"""
        print(f"Step: {self.current_step}, State: {self.state}")

# 使用Gym环境
def create_environment(env_name="CartPole-v1"):
    """创建Gym环境"""
    env = gym.make(env_name)
    print(f"环境: {env_name}")
    print(f"状态空间: {env.observation_space}")
    print(f"动作空间: {env.action_space}")
    return env

# 环境测试
env = create_environment()
state = env.reset()
print(f"初始状态: {state}")

# 随机动作测试
for i in range(5):
    action = env.action_space.sample()
    next_state, reward, done, info = env.step(action)
    print(f"动作: {action}, 奖励: {reward}, 完成: {done}")
    if done:
        break
env.close()

4.2.2 经验回放缓冲区

经验回放是深度强化学习中的重要技术，能够提高样本效率和训练稳定性：

import random
from collections import deque

class ReplayBuffer:
    """经验回放缓冲区"""
    def __init__(self, capacity):
        self.buffer = deque(maxlen=capacity)
        self.capacity = capacity
    
    def push(self, state, action, reward, next_state, done):
        """添加经验"""
        self.buffer.append((state, action, reward, next_state, done))
    
    def sample(self, batch_size):
        """随机采样批次"""
        batch = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = map(np.stack, zip(*batch))
        return state, action, reward, next_state, done
    
    def __len__(self):
        return len(self.buffer)

class PrioritizedReplayBuffer:
    """优先经验回放缓冲区"""
    def __init__(self, capacity, alpha=0.6):
        self.capacity = capacity
        self.alpha = alpha
        self.buffer = []
        self.priorities = []
        self.position = 0
    
    def push(self, state, action, reward, next_state, done):
        """添加经验"""
        max_priority = max(self.priorities) if self.priorities else 1.0
        
        if len(self.buffer) < self.capacity:
            self.buffer.append((state, action, reward, next_state, done))
            self.priorities.append(max_priority)
        else:
            self.buffer[self.position] = (state, action, reward, next_state, done)
            self.priorities[self.position] = max_priority
        
        self.position = (self.position + 1) % self.capacity
    
    def sample(self, batch_size, beta=0.4):
        """基于优先级采样"""
        if len(self.buffer) == 0:
            return None, None, None
        
        # 计算采样概率
        priorities = np.array(self.priorities[:len(self.buffer)])
        probs = priorities ** self.alpha
        probs /= probs.sum()
        
        # 采样索引
        indices = np.random.choice(len(self.buffer), batch_size, p=probs)
        
        # 计算重要性采样权重
        weights = (len(self.buffer) * probs[indices]) ** (-beta)
        weights /= weights.max()
        
        # 获取批次数据
        batch = [self.buffer[idx] for idx in indices]
        state, action, reward, next_state, done = map(np.stack, zip(*batch))
        
        return (state, action, reward, next_state, done), indices, weights
    
    def update_priorities(self, indices, priorities):
        """更新优先级"""
        for idx, priority in zip(indices, priorities):
            self.priorities[idx] = priority
    
    def __len__(self):
        return len(self.buffer)

# 使用示例
buffer = ReplayBuffer(capacity=10000)
prioritized_buffer = PrioritizedReplayBuffer(capacity=10000)

# 添加一些经验
for i in range(100):
    state = np.random.randn(4)
    action = np.random.randint(0, 2)
    reward = np.random.randn()
    next_state = np.random.randn(4)
    done = np.random.choice([True, False])
    
    buffer.push(state, action, reward, next_state, done)
    prioritized_buffer.push(state, action, reward, next_state, done)

print(f"普通缓冲区大小: {len(buffer)}")
print(f"优先缓冲区大小: {len(prioritized_buffer)}")

# 采样测试
batch = buffer.sample(32)
print(f"采样批次大小: {len(batch[0])}")

prioritized_batch = prioritized_buffer.sample(32)
if prioritized_batch[0] is not None:
    print(f"优先采样批次大小: {len(prioritized_batch[0][0])}")

4.2.3 训练循环

import time
from tqdm import tqdm

class Trainer:
    """强化学习训练器"""
    def __init__(self, agent, env, buffer, config):
        self.agent = agent
        self.env = env
        self.buffer = buffer
        self.config = config
        
        # 训练统计
        self.episode_rewards = []
        self.episode_lengths = []
        self.losses = []
        
        # 评估统计
        self.eval_rewards = []
        self.eval_episodes = 100
    
    def train_episode(self):
        """训练一个回合"""
        state = self.env.reset()
        episode_reward = 0
        episode_length = 0
        
        for step in range(self.config['max_steps']):
            # 选择动作
            if len(self.buffer) < self.config['min_buffer_size']:
                action = self.env.action_space.sample()  # 随机动作
            else:
                action = self.agent.select_action(state, epsilon=self.config['epsilon'])
            
            # 执行动作
            next_state, reward, done, info = self.env.step(action)
            
            # 存储经验
            self.buffer.push(state, action, reward, next_state, done)
            
            # 更新智能体
            if len(self.buffer) >= self.config['min_buffer_size']:
                loss = self.agent.update(self.buffer, self.config['batch_size'])
                if loss is not None:
                    self.losses.append(loss)
            
            state = next_state
            episode_reward += reward
            episode_length += 1
            
            if done:
                break
        
        self.episode_rewards.append(episode_reward)
        self.episode_lengths.append(episode_length)
        
        return episode_reward, episode_length
    
    def train(self, num_episodes):
        """训练多个回合"""
        print(f"开始训练 {num_episodes} 个回合...")
        
        for episode in tqdm(range(num_episodes)):
            # 训练一个回合
            reward, length = self.train_episode()
            
            # 更新探索率
            if self.config['epsilon'] > self.config['epsilon_min']:
                self.config['epsilon'] *= self.config['epsilon_decay']
            
            # 定期评估
            if episode % self.config['eval_interval'] == 0:
                eval_reward = self.evaluate()
                self.eval_rewards.append(eval_reward)
                print(f"回合 {episode}: 训练奖励={reward:.2f}, 评估奖励={eval_reward:.2f}")
            
            # 定期保存模型
            if episode % self.config['save_interval'] == 0:
                self.agent.save_model(f"model_episode_{episode}.pth")
    
    def evaluate(self):
        """评估智能体性能"""
        total_rewards = []
        
        for _ in range(self.eval_episodes):
            state = self.env.reset()
            episode_reward = 0
            
            for _ in range(self.config['max_steps']):
                action = self.agent.select_action(state, epsilon=0)  # 贪婪策略
                state, reward, done, _ = self.env.step(action)
                episode_reward += reward
                
                if done:
                    break
            
            total_rewards.append(episode_reward)
        
        return np.mean(total_rewards)
    
    def plot_training_progress(self):
        """绘制训练进度"""
        fig, axes = plt.subplots(2, 2, figsize=(12, 8))
        
        # 回合奖励
        axes[0, 0].plot(self.episode_rewards)
        axes[0, 0].set_title('Episode Rewards')
        axes[0, 0].set_xlabel('Episode')
        axes[0, 0].set_ylabel('Reward')
        
        # 回合长度
        axes[0, 1].plot(self.episode_lengths)
        axes[0, 1].set_title('Episode Lengths')
        axes[0, 1].set_xlabel('Episode')
        axes[0, 1].set_ylabel('Length')
        
        # 损失
        if self.losses:
            axes[1, 0].plot(self.losses)
            axes[1, 0].set_title('Training Loss')
            axes[1, 0].set_xlabel('Update Step')
            axes[1, 0].set_ylabel('Loss')
        
        # 评估奖励
        if self.eval_rewards:
            axes[1, 1].plot(self.eval_rewards)
            axes[1, 1].set_title('Evaluation Rewards')
            axes[1, 1].set_xlabel('Evaluation')
            axes[1, 1].set_ylabel('Reward')
        
        plt.tight_layout()
        plt.show()

# 训练配置
config = {
    'max_steps': 200,
    'min_buffer_size': 1000,
    'batch_size': 64,
    'epsilon': 1.0,
    'epsilon_min': 0.01,
    'epsilon_decay': 0.995,
    'eval_interval': 100,
    'save_interval': 500
}

print("训练配置设置完成！")

4.3 评估方法

4.3.1 性能指标

强化学习系统的评估需要多个维度的指标：

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns

class PerformanceEvaluator:
    """强化学习性能评估器"""
    
    def __init__(self):
        self.metrics = {}
    
    def calculate_basic_metrics(self, rewards, lengths):
        """计算基础性能指标"""
        metrics = {
            'mean_reward': np.mean(rewards),
            'std_reward': np.std(rewards),
            'median_reward': np.median(rewards),
            'min_reward': np.min(rewards),
            'max_reward': np.max(rewards),
            'mean_length': np.mean(lengths),
            'std_length': np.std(lengths),
            'success_rate': np.mean([r > 0 for r in rewards])  # 假设正奖励表示成功
        }
        return metrics
    
    def calculate_learning_metrics(self, rewards, window_size=100):
        """计算学习相关指标"""
        if len(rewards) < window_size:
            return {}
        
        # 滑动平均
        moving_avg = []
        for i in range(window_size, len(rewards) + 1):
            moving_avg.append(np.mean(rewards[i-window_size:i]))
        
        # 学习曲线斜率
        x = np.arange(len(moving_avg))
        slope, intercept, r_value, p_value, std_err = stats.linregress(x, moving_avg)
        
        # 收敛性分析
        convergence_point = self._find_convergence_point(moving_avg)
        
        metrics = {
            'learning_slope': slope,
            'learning_r_squared': r_value ** 2,
            'convergence_episode': convergence_point,
            'final_performance': moving_avg[-1] if moving_avg else 0,
            'performance_improvement': moving_avg[-1] - moving_avg[0] if moving_avg else 0
        }
        return metrics
    
    def _find_convergence_point(self, moving_avg, threshold=0.05):
        """找到收敛点"""
        if len(moving_avg) < 50:
            return len(moving_avg)
        
        # 计算性能变化的相对标准差
        recent_performance = moving_avg[-20:]
        if len(recent_performance) < 20:
            return len(moving_avg)
        
        cv = np.std(recent_performance) / np.mean(recent_performance)
        
        # 如果变异系数小于阈值，认为已收敛
        if cv < threshold:
            return len(moving_avg) - 20
        
        return len(moving_avg)
    
    def calculate_sample_efficiency(self, rewards, target_performance=0.8):
        """计算样本效率"""
        if not rewards:
            return {}
        
        max_reward = np.max(rewards)
        if max_reward == 0:
            return {}
        
        # 找到达到目标性能的回合
        target_reward = target_performance * max_reward
        episodes_to_target = None
        
        for i, reward in enumerate(rewards):
            if reward >= target_reward:
                episodes_to_target = i + 1
                break
        
        metrics = {
            'episodes_to_target': episodes_to_target,
            'sample_efficiency': 1.0 / episodes_to_target if episodes_to_target else 0,
            'target_performance': target_performance,
            'target_reward': target_reward
        }
        return metrics

# 使用示例
evaluator = PerformanceEvaluator()

# 模拟一些实验结果
np.random.seed(42)
rewards = np.random.normal(100, 20, 1000)
lengths = np.random.normal(200, 50, 1000)

# 计算指标
basic_metrics = evaluator.calculate_basic_metrics(rewards, lengths)
learning_metrics = evaluator.calculate_learning_metrics(rewards)
sample_metrics = evaluator.calculate_sample_efficiency(rewards)

print("基础指标:", basic_metrics)
print("学习指标:", learning_metrics)
print("样本效率指标:", sample_metrics)

5. SERL系列：样本高效机器人强化学习

我们根据SERL系列回溯，下面是从最新的工作一路回溯，RLDG(24年12月) → HIL-SERL(24年10月) → SERL(24年1月底)/FMB(24年1月中旬) → RLPD(23年2月)。

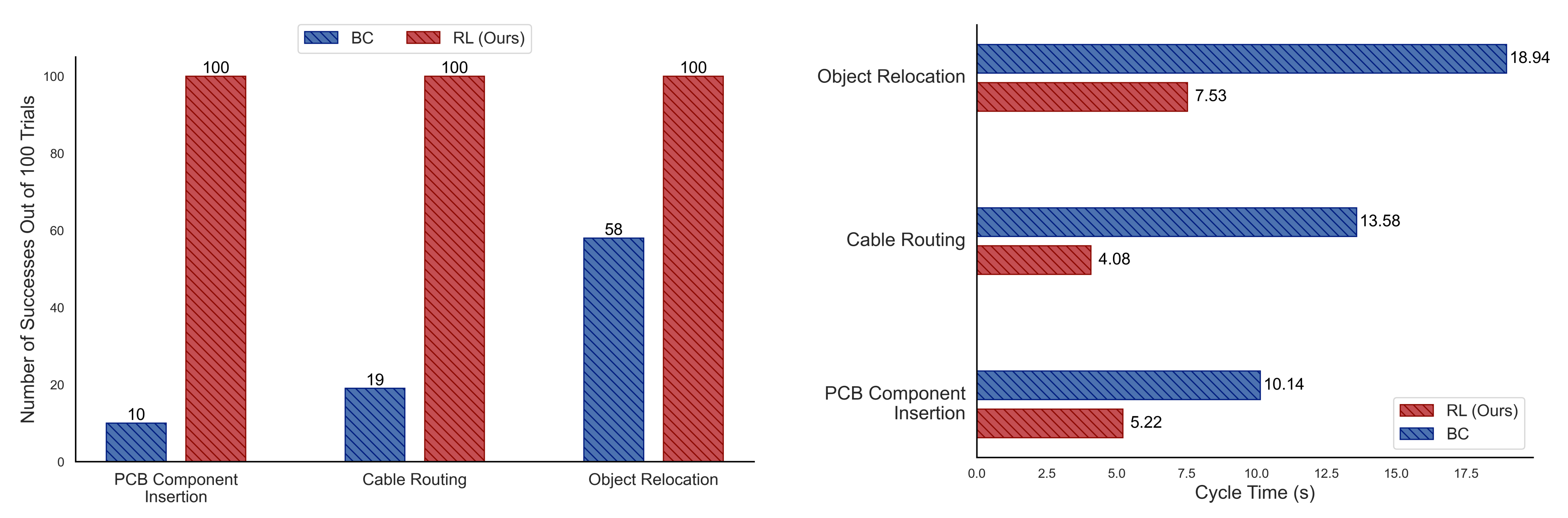
为满足“真机少样本、高可靠、可部署”的目标，SERL将高样本效率的离策略RL、基于视觉的奖励学习、自动重置与安全阻抗控制整合为一体，形成从感知到控制的闭环系统。下图展示了SERL在真实环境中的多任务表现（PCB插入、线缆布线、物体搬运）。

5.1 系统与方法总览

• 观测：多相机RGB（腕部/侧视）+ 本体感知（末端执行器位姿、力/力矩等）
• 动作：以末端执行器坐标系输出6D扭转（相对坐标系，便于空间泛化）
• 算法：RLPD（基于SAC的高UTD离策略方法）+ 对称采样（先验/在线各50%）
• 奖励：二元分类器/VICE（从像素学习“成功”信号，兼容稀疏奖励）
• 控制：阻抗控制器（含参考限制），兼顾安全与精细接触

5.2 RLPD核心细节：对称采样与高UTD

RLPD在训练时以高UTD比重复利用数据，并在“先验数据（离线演示/历史数据）”与“在线RL数据”之间执行对称采样，有效提升样本效率与稳定性。

# 伪代码：RLPD训练步（对称采样 + 高UTD）
for env_step in range(num_env_steps):
    transition = env.step(policy)
    rl_buffer.add(transition)

    for _ in range(utd_ratio):
        batch_off = offline_buffer.sample(batch_size // 2)
        batch_on  = rl_buffer.sample(batch_size // 2)
        batch = merge(batch_off, batch_on)

        # Critic目标与损失（SAC风格）
        with torch.no_grad():
            a_next, logp_next = policy.sample(batch.s_next)
            q_target = target_q(batch.s_next, a_next) - alpha * logp_next
            y = batch.r + (1 - batch.done) * gamma * q_target
        q_loss = F.mse_loss(q(batch.s, batch.a), y)

        # Actor损失（熵正则）
        a_new, logp = policy.sample(batch.s)
        q_new = q(batch.s, a_new)
        pi_loss = (alpha * logp - q_new).mean()

        optimize(q_loss, pi_loss)

5.3 从像素学习奖励：二元分类器/VICE

对于难以手工设计奖励的真实任务，SERL使用“成功/失败”二分类器作为奖励模型，或采用VICE在训练中动态补充负样本以抑制“对抗性状态”。

import torch
import torch.nn as nn

class RewardClassifier(nn.Module):
    def __init__(self, state_dim):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(state_dim, 256), nn.ReLU(),
            nn.Linear(256, 256), nn.ReLU(),
            nn.Linear(256, 1), nn.Sigmoid()
        )
    def forward(self, s):
        return self.net(s)
    @torch.no_grad()
    def reward(self, s):
        p_success = self.forward(s).clamp(1e-6, 1-1e-6)
        return torch.log(p_success)

数据构成建议：正样本≈200帧、负样本≈1000帧（数分钟远程操作即可），离线训练达到>95%准确率后上线作为稀疏奖励；若出现“假阳性利用”，启用VICE迭代刷新负样本。

5.4 自动重置与相对坐标系

• 前向/后向策略：学习完成任务与回到起始态的双策略，减少人工复位成本
• 相对坐标系：观测与动作均以“末端执行器初始帧”为参照，模拟“目标在手中移动”，增强扰动/位姿变化下的泛化

# 相对位姿计算（示意）：T_b0_bt = inv(T_b0) @ T_bt，
# 将相对位姿特征投给策略；动作在当前末端坐标系中生成

5.5 真实任务与指标

• 任务：PCB连接器插入、线缆布线、自由物体重定位等
• 结果：15–60分钟/策略即收敛，三类任务均可达接近100%成功率；周期时间较BC基线提升至约1.8×（更快）
• 关键对比：等量人类介入下，HIL-SERL（RL+纠正）成功率与效率显著优于HG-DAgger/BC/扩散策略

5.6 视觉骨干与多相机融合：鲁棒表征与轻量推理

在真实世界中，照明、反光、遮挡和动态背景都会干扰策略对关键几何关系的感知。实践中推荐采用“轻量主干 + 多视角特征对齐”的组合：以 ImageNet 预训练的 ResNet-10/18 作为主干，分别编码腕部与侧视相机图像，随后对多视角特征做通道级加权与空间级 ROI 对齐，再与本体感知特征拼接输入策略。这样既保证了推理延迟（10–20Hz 控制频率下的毫秒级前向）又维持了在插拔等精细操作中对接触前微位姿的分辨能力。训练时可引入颜色抖动、仿射扰动与 CutMix 以提升泛化。

# 简化版：多相机特征融合模块（PyTorch）
class MultiCamFusion(nn.Module):
    def __init__(self, backbone: nn.Module, feat_dim: int = 256):
        super().__init__()
        self.backbone = backbone  # 共享权重
        self.channel_attn = nn.Sequential(
            nn.AdaptiveAvgPool2d(1),
            nn.Conv2d(feat_dim, feat_dim // 4, 1), nn.ReLU(),
            nn.Conv2d(feat_dim // 4, feat_dim, 1), nn.Sigmoid()
        )
        self.roi_align = torchvision.ops.RoIAlign(output_size=(14,14), spatial_scale=1/8, sampling_ratio=2)
        self.head = nn.Sequential(nn.Flatten(), nn.Linear(feat_dim*14*14, 512), nn.ReLU())
    def forward(self, imgs, rois):  # imgs: [B, V, C, H, W], rois: 每视角候选框
        feats = []
        for v in range(imgs.size(1)):
            f = self.backbone(imgs[:, v])  # [B, feat_dim, h, w]
            w = self.channel_attn(f)
            f = f * w
            f = self.roi_align(f, rois[v])
            feats.append(f)
        fused = torch.stack(feats, dim=1).mean(1)
        return self.head(fused)

…详情请参照古月居