连续信号&离散信号的功率谱密度--用MATLAB求功率谱密度

一直对数字信号处理中的功率谱密度计算有点好奇，虽然MATLAB有提供现成的计算功率谱密度的计算函数，但还是想不通过调用函数，就单纯的通过FFT变换利用所谓的周期图法，去计算信号的功率谱密度，于是就有了下文。

迎风打盹儿

4269人浏览 · 2024-03-28 16:19:12

迎风打盹儿 · 2024-03-28 16:19:12 发布

连续信号&离散信号的功率谱密度--用MATLAB求功率谱密度

前言

提示：以下是本篇文章正文内容，希望能帮助到各位，转载请附上链接。

一、能量及功率定义

1、连续信号

连续信号 $x(t)$ 的能量定义为：

$E=\int_{-\infty }^{+\infty}x^2(t)dt$

功率定义为:

$P=\lim_{t \to\infty }\frac{1}{2T}\int_{-T}^{T}x^2(t)dt$

2、离散信号

序列 $x(n)$ 的能量定义为：

$E=\sum_{n=-\infty}^{\infty}|x(n)|^{2}=\sum_{n=-\infty}^{\infty}x(n)x^{*}(n)$

功率定义为:

$P=\lim\limits_{K\to\infty}\frac{1}{2K+1}\sum\limits_{n=-K}^{K}\left | x(n) \right |^2$

按照定义，对于离散信号，在固定的时间内，采样频率增加，采样点数增加，能量是会增加。

无意中看到的新观点，采样频率增加会导致能量增加。感觉怪怪的，但又与公式吻合，分享给大家。

用MATLAB验证了一下，采样点数增加，能量是会增加，但功率不变。

二、帕塞瓦尔定理

1、连续信号

$\int_{-\infty}^\infty\left|x(t)\right|^2\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^\infty\left|X(e^{j\omega})\right|^2\mathrm{d}\omega=\int_{-\infty}^\infty\left|X(e^{j2\pi f})\right|^2\mathrm{d}f$

2、离散信号

$\begin{aligned}\sum_{n=0}^{N-1}|x(n)|^2&=\frac{1}{N}\sum_{k=0}^{N-1}|X(k)|^2=\frac{1}{N}\sum_{k=0}^{N-1}|DFT[x(n)]|^2\end{aligned}$

三、功率谱密度计算公式

用于功率谱密度估计的公式有如下：

1）连续时间信号：

$S_{xx}(f)=\lim_{T\to\infty}\frac{|\mathcal{F}\{x_w(t)\}|^2}T;$

2）离散时间信号：

$S_{xx}(f)=\lim_{N\to\infty}\frac1{Nf_s}|\mathrm{DFT}\{x(n)\}|^2$

对于离散时间信号求功率谱密度，为什么要除以采样频率Fs，要用离散信号去推，比较复杂，本人不搞谱估计，就不细推了，大家可以参考下面几篇文章。

功率谱密度为什么等于fft的平方除N再除以fs？ - 知乎

功率谱密度(Power Spectrum Density, PSD)的公式推导与谱密度估计 - 知乎

使用 FFT 获得功率频谱密度估计- MATLAB & Simulink- MathWorks 中国

四、MATLAB仿真

1、源代码

clear ; clc; close all;

randn('state',0);                    % 随机数初始化
Fs = 1000;                           % 采样频率
t = 0:1/Fs:1-1/Fs;                   % 时间刻度
f1=50; f2=120;                       % 两个正弦分量频率
x=cos(2*pi*f1*t)+3*cos(2*pi*f2*t)+randn(size(t)); % 信号
% 使用FFT
N = length(x);                       % x长度
xdft = fft(x);                       % FFT
xdft = xdft(1:N/2+1);                % 取正频率
psdx = (1/(Fs*N)) * abs(xdft).^2;    % 计算功率谱密度
psdx(2:end-1) = 2*psdx(2:end-1);     % 乘2(2:end-1)
freq = 0:Fs/length(x):Fs/2;          % 频率刻度
subplot 211
plot(freq,10*log10(psdx))        % 取对数作图
grid on; xlim([0 Fs/2]);
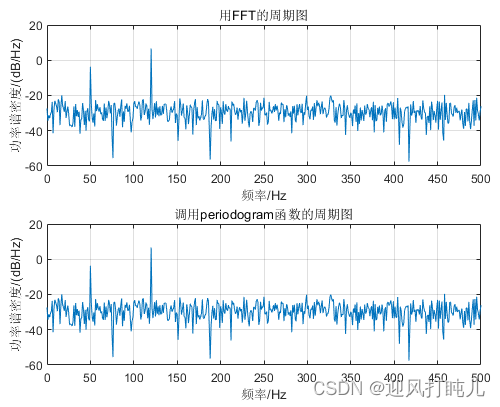
title('用FFT的周期图')
xlabel('频率/Hz')
ylabel('功率谱密度/(dB/Hz)')
% 调用periodogram函数
[Pxx,f]=periodogram(x,rectwin(length(x)),N,Fs); 
subplot 212
plot(freq,10*log10(Pxx));        % 取对数作图
grid on; xlim([0 Fs/2]);
title('调用periodogram函数的周期图')
xlabel('频率/Hz')
ylabel('功率谱密度/(dB/Hz)')
mxerr = max(psdx'-Pxx)               % 求两种方法的最大差值
set(gcf,'color','w'); 

P = Fs/N * (sum(psdx) - 0.5*(psdx(1) + psdx(end))) %梯形法积分

其中用到函数 [Pxx,f] = periodogram(x,rectwin(length(x)),N,Fs);

括号里面的参数依次为：序列，矩形窗，FFT长度，采样频率。