SVM -- Hard Margin SVM
SVM科目: 白板推导机器学习Support Vector Machine 在深度学习流行之前,支持向量机是非常流行的算法。 本讲主要从理论推导方面介绍,怎么从一步一步的演化到最后的优化问题。 从核心概念上来看,有一句关于支持向量机的口头禅: –SVM 有三宝,间隔、对偶、核技巧.注意: 其中的“核技巧”和 SVM 之间并没有固定的联系。实际上,在 SVM 出现之前就已...
SVM
科目: 白板推导机器学习
Support Vector Machine
在深度学习流行之前,支持向量机是非常流行的算法。
本讲主要从理论推导方面介绍,怎么从一步一步的演化到最后的优化问题。
从核心概念上来看,有一句关于支持向量机的口头禅:
– SVM 有三宝,间隔、对偶、核技巧.
注意: 其中的“核技巧”和 SVM 之间并没有固定的联系。实际上,在 SVM 出现之前就已经有了核技巧、核函数了。只不过核技巧和让 SVM 从普通的欧式空间(特征空间)映射到高维的空间,从而可以实现一定的非线性分类。
从类别上 SVM 可以分类为:
- Hard-Margin SVM
- Soft-Margin SVM
- Kernel SVM
Hard-Margin SVM
先从几何角度来看 SVM:
首先, SVM 起初是为了解决二分类问题而引出的。

分类模型:
f ( w ) = s i g n ( w T x + b ) f(w) = sign(w^{T}x+b) f(w)=sign(wTx+b)
所以,SVM 本质上是一个判别模型,和概率没有关系。
最大间隔分类器:
{ m a x ∗ m a r g i n ( w , b ) s . t . y i = + 1 , i f : w T x i + b > 0 , y i = − 1 , i f : w T x i + b < 0. \left\{\begin{matrix} max*margin(w, b)\\ s.t.y_{i}=+1, if: w^{T}x_{i}+b>0, y_{i}=-1, if : w^{T}x_{i}+b<0. \end{matrix}\right. {max∗margin(w,b)s.t.yi=+1,if:wTxi+b>0,yi=−1,if:wTxi+b<0.
简化成:
{ m a x ∗ m a r g i n ( w , b ) s . t . : y i ( w T x i + b ) > 0 , f o r : ∀ i = 1 , . . . , N . \left\{\begin{matrix} max*margin(w, b)\\ s.t.:y_{i}(w^{T}x_{i}+b)>0, for: \forall i=1,...,N. \end{matrix}\right. {max∗margin(w,b)s.t.:yi(wTxi+b)>0,for:∀i=1,...,N.
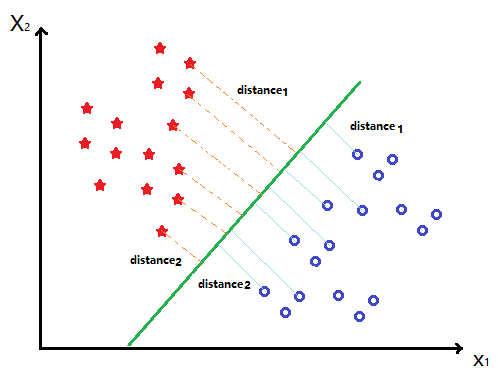
m a r g i n ( w , b ) = m i n w , b , x i , i = 1 , . . . , N d i s t a n c e ( w , b , x i ) , margin(w, b) = min_{w,b,x_{i}, i=1,...,N} distance(w, b, x_{i}), margin(w,b)=minw,b,xi,i=1,...,Ndistance(w,b,xi),
= m i n w , b , x i 1 ∣ ∣ w ∣ ∣ ∣ w T x i + b ∣ . = min_{w,b,x_{i}} \frac{1}{||w||}|w^{T}x_{i}+b|. =minw,b,xi∣∣w∣∣1∣wTxi+b∣.
基于上式,由于 y i ( w T x i + b ) > 0 y_{i}(w^{T}x_{i}+b)>0 yi(wTxi+b)>0,同时 y i y_{i} yi 只能取值:+1/-1,所以:
{ m a x w , b ∗ m i n x i 1 ∣ ∣ w ∣ ∣ y i ( w T x i + b ) s . t . y i ( w T x i + b ) > 0. \left\{\begin{matrix} max_{w,b}*min_{x_{i}} \frac{1}{||w||}y_{i}(w^{T}x_{i}+b) \\ s.t. y_{i}(w^{T}x_{i}+b)>0. \end{matrix}\right. {maxw,b∗minxi∣∣w∣∣1yi(wTxi+b)s.t.yi(wTxi+b)>0.
对于 s . t . y i ( w T x i + b ) > 0 s.t. y_{i}(w^{T}x_{i}+b)>0 s.t.yi(wTxi+b)>0,可以等价于: ∃ r > 0 , s . t . m i n x i , y i , i = 1 , . . . N y i ( w T x i + b ) = r . \exists r>0, s.t. min_{x_{i}, y_{i},i=1,...N}y_{i}(w^{T}x_{i}+b)=r. ∃r>0,s.t.minxi,yi,i=1,...Nyi(wTxi+b)=r.
由于对直线方程的系数进行同比例缩放,并不影响直线方程的结果。所以,上式中的 r ,可以取值为 1.
即:
{ m a x w , b 1 ∣ ∣ w ∣ ∣ , s . t . m i n y i ( w T x i + b ) = 1 , o r : s . t . y i ( w T x i + b ) ≥ 1. \left\{\begin{matrix} max_{w,b}\frac{1}{||w||},\\ s.t. min_{y_{i}(w^{T}x_{i}+b)=1},or:s.t.y_{i}(w^{T}x_{i}+b) \geq 1. \end{matrix}\right. {maxw,b∣∣w∣∣1,s.t.minyi(wTxi+b)=1,or:s.t.yi(wTxi+b)≥1.
通常情况下,优化问题习惯上是求解最小化问题,上式可以等价于:
{ m i n w , b 1 2 w T w s . t . y i ( w T x i + b ) ≥ 1 , f o r ∀ i = 1 , . . . , N . \left\{\begin{matrix} min_{w, b}\frac{1}{2}w^{T}w\\ s.t. y_{i}(w^{T}x_{i}+b) \geq 1, for \forall i=1,...,N. \end{matrix}\right. {minw,b21wTws.t.yi(wTxi+b)≥1,for∀i=1,...,N.
D a t a = { ( x i , y i ) } i = 1 N , x i ∈ R p , y i ∈ { + 1 , − 1 } . Data = \{(x_{i}, y_{i})\}_{i=1}^{N}, x_{i} \in R^{p}, y_{i} \in \{+1, -1\}. Data={(xi,yi)}i=1N,xi∈Rp,yi∈{+1,−1}.
对于(w, b)而言的带约束的原优化问题:
{ m i n w , b 1 2 w T w , s . t . y i ( w T x i + b ) ≥ 1. \left\{\begin{matrix} min_{w,b}\frac{1}{2}w^{T}w,\\ s.t. y_{i}(w^{T}x_{i}+b)\geq 1. \end{matrix}\right. {minw,b21wTw,s.t.yi(wTxi+b)≥1.
转换成拉格朗日形式:
L ( w , b , λ ) = 1 2 w T w + ∑ i = 1 N λ i ( 1 − y i ( w T x i + b ) ) . L(w,b,\lambda ) = \frac{1}{2}w^{T}w + \sum_{i=1}^{N}\lambda_{i}(1-y_{i}(w^{T}x_{i}+b)). L(w,b,λ)=21wTw+i=1∑Nλi(1−yi(wTxi+b)).
其无约束的原优化问题:
{ m i n w , b ∗ m a x λ L ( w , b , λ ) , s . t . λ i ≥ 0. \left\{\begin{matrix} min_{w,b}*max_{\lambda} L(w,b,\lambda),\\ s.t. \lambda_{i} \geq 0. \end{matrix}\right. {minw,b∗maxλL(w,b,λ),s.t.λi≥0.

- 如果 1 − y i ( w T x i + b ) > 0 , m a x λ L ( w , b , λ ) = 1 2 w T w + ∞ = ∞ 1-y_{i}(w^{T}x_{i}+b) > 0, max_{\lambda}L(w,b,\lambda) = \frac{1}{2}w^{T}w + \infty = \infty 1−yi(wTxi+b)>0,maxλL(w,b,λ)=21wTw+∞=∞,
- 如果 1 − y i ( w T x i + b ) ≤ 0 , m a x λ L ( w , b , λ ) = 1 2 w T w + 0 = 1 2 w T w , m i n w , b ∗ m a x λ L = m i n w , b 1 2 w T w . 1-y_{i}(w^{T}x_{i}+b) \leq 0, max_{\lambda}L(w,b,\lambda)=\frac{1}{2}w^{T}w + 0 = \frac{1}{2}w^{T}w, min_{w,b}*max_{\lambda}L = min_{w,b}\frac{1}{2}w^{T}w. 1−yi(wTxi+b)≤0,maxλL(w,b,λ)=21wTw+0=21wTw,minw,b∗maxλL=minw,b21wTw.
综合上述两式:
m i n w , b ∗ m a x λ L ( w , b , λ ) = m i n w , b ( ∞ , 1 2 w T w ) = m i n w , b 1 2 w T w . min_{w,b}*max_{\lambda}L(w,b,\lambda) = min_{w,b}(\infty, \frac{1}{2}w^{T}w) = min_{w,b}\frac{1}{2}w^{T}w. minw,b∗maxλL(w,b,λ)=minw,b(∞,21wTw)=minw,b21wTw.
也即:
原问题的约束形式 <==>(等价于) 原问题的无约束形式.
原问题的对偶问题:
{ m a x λ ∗ m i n w , b L ( w , b , λ ) , s . t . λ i ≥ 0. \left\{\begin{matrix} max_{\lambda}*min_{w,b}L(w,b,\lambda),\\s.t. \lambda_{i} \geq 0. \end{matrix}\right. {maxλ∗minw,bL(w,b,λ),s.t.λi≥0.
针对 m i n w , b L ( w , b , λ ) min_{w,b}L(w,b,\lambda) minw,bL(w,b,λ) 进行推导:
令 ∂ L ∂ b = 0 \frac{\partial L}{\partial b} = 0 ∂b∂L=0 推导出=> ∑ i = 1 N λ i y i = 0 \sum_{i=1}^{N}\lambda_{i}y_{i}=0 ∑i=1Nλiyi=0.
将其代入: L ( w , b , λ ) L(w,b,\lambda) L(w,b,λ):
L ( w , b , λ ) = 1 2 w T w + ∑ i = 1 N λ i − ∑ i = 1 N λ i y i ( w T x i + b ) = 1 2 w T w + ∑ i = 1 N λ i − ∑ i = 1 N λ i y i w T x i + ∑ i = 1 N λ i y i b = 1 2 w T w + ∑ i = 1 N λ i − ∑ i = 1 N λ i w T x i L(w,b,\lambda) = \frac{1}{2}w^{T}w + \sum_{i=1}^{N}\lambda_{i} - \sum_{i=1}^{N}\lambda_{i}y_{i}(w^{T}x_{i}+b) = \frac{1}{2}w^{T}w + \sum_{i=1}^{N}\lambda_{i} - \sum_{i=1}^{N}\lambda_{i}y_{i}w^{T}x_{i} + \sum_{i=1}^{N}\lambda_{i}y_{i}b = \frac{1}{2}w^{T}w + \sum_{i=1}^{N}\lambda_{i} - \sum_{i=1}^{N}\lambda_{i}w^{T}x_{i} L(w,b,λ)=21wTw+i=1∑Nλi−i=1∑Nλiyi(wTxi+b)=21wTw+i=1∑Nλi−i=1∑NλiyiwTxi+i=1∑Nλiyib=21wTw+i=1∑Nλi−i=1∑NλiwTxi
令 ∂ L ∂ w = w − ∑ i = 1 N λ i y i x i = 0 \frac{\partial L}{\partial w} = w- \sum_{i=1}^{N}\lambda_{i}y_{i}x_{i} = 0 ∂w∂L=w−∑i=1Nλiyixi=0,推导出:
w ∗ = ∑ i = 1 N λ i y i x i . w^{*} = \sum_{i=1}^{N}\lambda_{i}y_{i}x_{i}. w∗=i=1∑Nλiyixi.
m i n L ( w , b , λ ) = 1 2 ( ∑ i = 1 N λ i y i x i ) T ( ∑ i = 1 N λ i y i x i ) − ∑ i = 1 N λ i y i ( ∑ j = 1 N λ i y j x j ) T x i + ∑ i = 1 N λ i = − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j x i T x j + ∑ i = 1 N λ i . minL(w,b,\lambda)=\frac{1}{2}(\sum_{i=1}^{N}\lambda_{i}y_{i}x_{i})^{T}(\sum_{i=1}^{N}\lambda_{i}y_{i}x_{i}) - \sum_{i=1}^{N}\lambda_{i}y_{i}(\sum_{j=1}^{N}\lambda_{i}y_{j}x_{j})^{T}x_{i} + \sum_{i=1}^{N}\lambda_{i} = -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum_{i=1}^{N}\lambda_{i}. minL(w,b,λ)=21(i=1∑Nλiyixi)T(i=1∑Nλiyixi)−i=1∑Nλiyi(j=1∑Nλiyjxj)Txi+i=1∑Nλi=−21i=1∑Nj=1∑NλiλjyiyjxiTxj+i=1∑Nλi.
最终,对偶问题有如下形式:
{ m a x λ − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j x i T x j + ∑ i = 1 N λ i , s . t . λ i ≥ 0 , ∑ i = 1 N λ i y i = 0. \left\{\begin{matrix} max_{\lambda}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum_{i=1}^{N}\lambda_{i},\\s.t. \lambda_{i} \geq 0, \sum_{i=1}^{N}\lambda_{i}y_{i}=0. \end{matrix}\right. {maxλ−21∑i=1N∑j=1NλiλjyiyjxiTxj+∑i=1Nλi,s.t.λi≥0,∑i=1Nλiyi=0.
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容














所有评论(0)