马尔科夫决策过程

强化学习基本框架

智能体与环境不断交互从而产生很多的数据，强化学习算法利用产生的数据修改自身的动作策略。

强化学习与深度学习的区别：
深度学习如图像识别和语音识别，解决的是感知的问题。
强化学习解决的是决策的问题。

马尔科夫决策过程（MDP）是一个能够解决大部分强化学习问题的框架。

理论讲解

马尔科夫性

马尔科夫性指系统的下一个状态St+1仅与当前状态St有关，而与以前的状态无关。
由此定义：状态St是马尔科夫的，当且仅当P[St+1| St] = P[St+1 | S1,S2,……,St]
即：一旦当前状态已知，历史状态就会被抛弃

马尔科夫过程

马尔科夫过程的定义：
马尔科夫过程 是一个二元组（S，P），且满足S是有限状态集合，P是状态转移矩阵。

马尔科夫过程中不存在动作和奖励。

将动作（策略）和回报考虑在内的马尔科夫过程称为马尔科夫决策过程。

马尔科夫决策过程

马尔科夫决策过程由元组（S，A，P，R，r）描述，其中：

• S: 有限的状态集
• A：有限的动作集
• P：状态转移概率
• R：回报函数
• r：折扣因子，用来计算累计回报。

马尔科夫决策过程的状态转移概率是包含动作的，既：

P = P[St+1 = s’ | St=s,A=a]

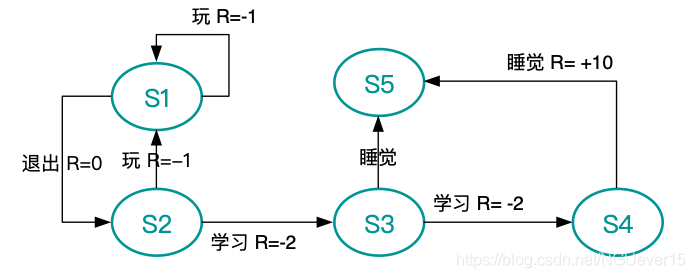
状态集S={s1,s2,s3,s4,s5}
动作集A={玩，退出，学习，睡觉}
立即回报用R标记

强化学习的目标 是给定一个马尔科夫决策过程，寻找最优策略。
所谓策略 是指状态到动作的映射。（即：确定每一个状态下该执行什么样的动作）

策略常用符号π表示，它指给定状态s时，动作集上的一个分布。
每一个agent都有自己的策略 ，强化学习是找到最优的策略，使得总体回报最大。

π[a|s] = p[At = a | St = s]

给定策略π时，可以根据公式计算累计回报：

累计回报用Gt表示。
因为π的随机性，所有Gt也是不确定的

从状态s1 出发，状态序列可能有多种情况：
s1→s2 → s3 → s4 → s5
s1→s2 → s3 → s5
……
而每一种状态序列都对应了一个概率和累计回报
所以后面考虑使用累计回报的期望来表示这个始发状态s1 的价值。

为了评价状态s1 的价值，我们需要定义一个确定来来描述价值
累计回报G1是个随机变量，但是其期望是个确定值，可以作为状态值函数的定义

状态值函数

当agent 采用策略π时，累计回报服从一个分布，累计回报在状态s处的期望值定义为状态-值函数：

状态值函数 是和策略π对应的，策略π改变，必然引起状态值函数的变化。

状态-行为值函数

相应的，状态-行为值函数为：

st是始发状态，At是始发动作，这两个参数是规定好了的。

状态值函数 和状态-行为值函数的关系为：
$${\upsilon }_{\pi }(s)=\sum _{a\in A}{q}_{\pi }(s,a)(6)$$

question 1

从一个状态到达另一个状态（直达）是否存在多种动作选择？ 或者说一个状态下指定一个动作，是否会达到两个不同的状态？

定义
最优状态值函数${\upsilon }^{\ast }(s)$为所有策略中对大的状态-行为值函数，即：
$${\upsilon }^{\ast }(s)=ma{x}_{\pi }{\upsilon }_{\pi }(s)(7)$$

最优状态-行为值函数$q^{\ast }(s,a)$为所有策略中对大的状态-行为值函数，即：
$$q^{\ast }(s,a)=ma{x}_{\pi }{q}_{\pi }(s,a)(8)$$

在已知最优状态-行为值函数的情况下，最优策略可以通过直接最大化$q^{\ast }(s,a)$来决定:
$${\pi }^{\ast }(a|s)=\left\{\begin{array}{c}1,a=\arg \max q^{\ast }(s,a)\\ 0,otherwise\end{array}\right\}(9)$$