隐马尔可夫模型(HMM)
隐马尔科夫模型(Hidden Markov Model,HMM)是离散状态的动态模型,用于对时间序列的分析研究,HMM属于生成模型在语音识别等领域有着广泛的应用。目录1.隐马尔可夫模型的基本概念1.1 隐马尔科夫模型定义及三要素1.1.1 HMM定义1.1.2 HMM三要素1.2隐马尔可夫模型的3个基本问题2.求值问题2.1 直接求值法2.2 前向算法2.3...
隐马尔科夫模型(Hidden Markov Model,HMM)是离散状态的动态模型,用于对时间序列的分析研究,HMM属于生成模型在语音识别等领域有着广泛的应用。
目录
1.隐马尔可夫模型的基本概念
1.1 隐马尔科夫模型定义及三要素
说到一个技术之前总是先说这个技术的概念,关于HMM的定义,引用李航博士的《统计学习方法》中的定义。
1.1.1 HMM定义
定义:隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。状态序列(state sequence)用S表示,观测序列(observation sequence)用O表示。
隐马尔科夫模型,我们从名字上就能看出它的特点,即:符合马尔可夫过程、观测序列由隐状态产生。
有关马尔科夫过程有两个假设:
(1)、齐次马尔科夫性假设。即马尔可夫链在任意时刻t的状态只与前一时刻t-1的状态有关,与其他时刻的状态和观测都无关,即有: 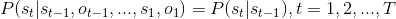
(2)、观测独立性假设。即任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
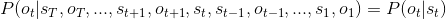
1.1.2 HMM三要素

如上图所示,是一个股市的简易图。其中Bull、Bear和Even分别表示牛市、熊市和平仓,它们表示股市的三种状态。从图中可以看到当前状态为Bull时,下一状态还是为Bull的概率为0.6,下一状态为Even的概率为0.2,下一概率为Bear的概率为0.2;同样的,当前状态为Bear时,下一状态还是Bear的概率为0.3,下一状态为Bull的概率为0.5,下一转态为Even的概率为0.2;但前状态为Even时,下一状态还是Even的概率为0.5,下一状态为Bull的概率为0.4,下一状态为Bear的概率为0.1。我们称这些概率为转移概率,用状态转移概率矩阵A表示为:

矩阵中的元素表示概率,以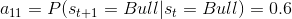
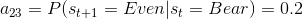
对于每一个状态都有三个虚线箭头指向的三个观测值,分别是:up、down和unchanged。以Bull状态为例,0.7表示在此状态下,股市上升的概率为0.7;0.1表示在此状态下,股市下降的概率为0.1;0.2表示在此状态下,股市不变的概率为0.2。我们把这些概率称为观测概率,把所有的观测概率用观测概率矩阵B表示为:

以矩阵B中的元素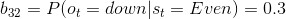
初始状态概率向量用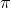
,其中,
是时刻t=1处于状态
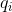
初始状态概率向量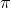
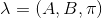
状态转移概率矩阵A与初始状态概率向量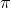
1.2隐马尔可夫模型的3个基本问题
(1) 概率计算问题,又称求值问题。给定模型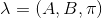
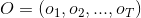
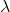
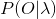
(2) 学习问题,又称模型的训练。已知观测序列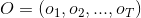
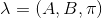
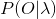
。
(3) 预测问题,又称解码问题(decoding)。已知模型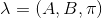
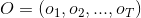
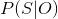
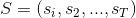
2.求值问题
求值问题就是在给定模型参数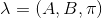
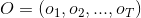
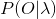
2.1 直接求值法
我们可以直接对其进行计算。
(2.1)
其中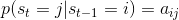
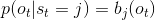
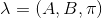
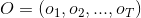
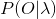

这种直接求解的方法在理论上是可行的,但是它的计算量很大,一共需要做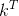
2.2 前向算法
前向概率:给定HMM参数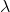
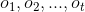
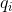
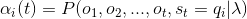
取t = 1,得到: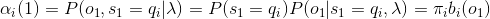
取t = 2,得到:

递归得:
![\alpha_{j}(T) = b_{j}(o_{T})[\sum_{i = 1}^{k}\alpha_{i}(T-1)a_{ij}]\\ =P(o_{1},o_{2},...,o_{T},s_{T} =q_{j} |\lambda)\\](https://img-blog.csdnimg.cn/20181225193257149)
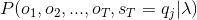
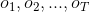
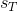
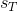
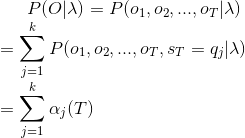
前向计算要比直接计算高效很多,其关键是局部计算前向概率,然后递推到全局。可以看到每一个时刻的前向概率只需要做k次加法运算,而下一时刻的计算直接引用前一时刻的计算结果,一共有T个时间点的话,那么用前向算法计算概率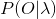
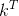
2.3 后向算法
后向概率:给定HMM参数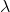
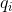
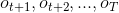
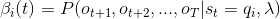
规定
取t = T-1得:

取t = T-2得

递归得: 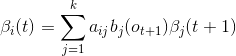
最后得到: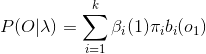
2.4 前向-后向算法
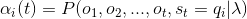
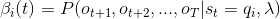

在求值时,可以用前向算法也可以用后向算法,还可以同时使用两种算法,下面举例说明一下。
2.4.1 单个状态概率计算公式
给定模型参数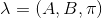
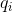
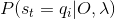
(2.9) 接下来求解概率
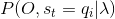

同样的得到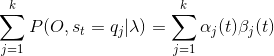
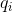
(2.10)
3.学习问题
HMM的学习问题就是求得参数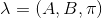
3.1 EM算法
训练数据只包含观测序列,而没有状态序列,这时我们可以吧状态序列看成隐变量S,那么HMM是一个含有隐变量的概率模型:
(3.1)
因为模型中含有隐变量,所以训练HMM时可使用EM算法迭代求解参数。
EM算法迭代求解参数步骤:
1、选择参数的初始值,得到模型
2、E步:E步是求期望,那么求得是谁的期望呢。求得是联合分布的对数似然函数以
为分布的期望,即
,这里需要对期望进行简单的修改:

修改后的期望定义为,其中
表示要极大化的HMM参数,
表示当前HMM参数的估计值。由(2.1)式得
(3.2)
将其带入函数得:
(3.3)
3、M步:最大化求模型参数
在式(3.3)中可以看到,函数分成了三个部分,可以分别求三个部分的最大值从而得到模型的参数
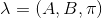
4、终止程序。得到模型参数
4.预测问题
预测问题就是给定模型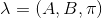
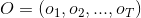
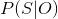
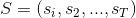
4.1 维特比算法
维特比算法是一种动态规划的算法,有关动态规划的解释可以查看参考文献3,文章用漫画的形式解释了动态规划,简单易懂。以维基百科的感冒发烧的例子进行说明。
假设村民的身体特质是理想的,要么健康要么发烧。假设某诊所的医生通过询问病人的感觉来诊断病人是否发烧,而村民只需要告诉医生感觉正常、头晕或冷。病人的状态有两种:‘健康’和‘发烧’,这个是医生无法直接观察到的,因此把它看做是隐状态;而村民告诉医生的感觉:正常、头晕和发烧是由病人状态决定的,这些看做是观测结果。那么这就是一个HMM的例子。
现假设有如下的HMM状态链。用参数表示为:
states = ('Healthy', 'Fever')
observations = ('normal', 'cold', 'dizzy')
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
transition_probability = {
'Healthy' : {'Healthy': 0.7, 'Fever': 0.3},
'Fever' : {'Healthy': 0.4, 'Fever': 0.6},
}
emission_probability = {
'Healthy' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6},
} 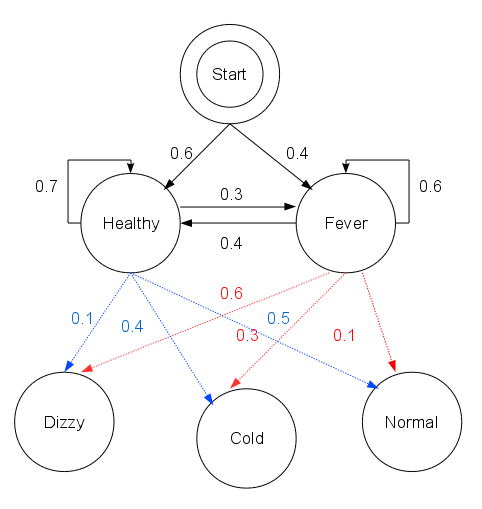
假设病人连续三天看医生,医生发现第一天他感觉正常,第二天感觉冷,第三天感觉头晕。 于是医生产生了一个问题:怎样的健康状态序列最能够解释这些观察结果。这个问题就可以用维特比算法解决。
def viterbi(obs, states, start_p, trans_p, emit_p):
V = [{}]
path = {}
# Initialize base cases (t == 0)
for y in states:
V[0][y] = start_p[y] * emit_p[y][obs[0]]
path[y] = [y]
# Run Viterbi for t > 0
for t in range(1,len(obs)):
V.append({})
newpath = {}
for y in states:
(prob, state) = max([(V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
V[t][y] = prob
newpath[y] = path[state] + [y]
# Don't need to remember the old paths
path = newpath
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
return (prob, path[state])
if __name__ == '__main__':
print(viterbi(observations, states, start_probability, transition_probability, emission_probability))
最后结果为:(0.01512, ['Healthy', 'Healthy', 'Fever'])。也就是说病人第一天健康,第二天也健康,第三天发烧产生上面的观测结果的概率最大,为0.01512。
| 输入: | 模型 |
|---|---|
| 输出: | 最优路径 |
| (1)、初始化 (2)、递推。对 (3)、终止 (4)、最优路径回溯。对 求得最优路径 | |
Viterbi算法其实就是多步骤每步多选择模型的最优选择问题,其在每一步的所有选择都保存了前续所有步骤到当前步骤当前选择的最小总代价(或者最大价值)以及当前代价的情况下前继步骤的选择。依次计算完所有步骤后,通过回溯的方法找到最优选择路径。
参考文献:
1.《统计学习方法》 李航
2. 徐亦达自频道 http://i.youku.com/i/UMzIzNDgxNTg5Ng==?spm=a2hzp.8253869.0.0
3. 漫画:什么是动态规划 https://juejin.im/post/5a29d52cf265da43333e4da7
4. 维特比算法 https://zh.wikipedia.org/wiki/%E7%BB%B4%E7%89%B9%E6%AF%94%E7%AE%97%E6%B3%95
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)