【图像处理】轮廓二阶矩计算目标中心-计算目标中心位置方法3
参考 http://blog.csdn.net/yang6464158/article/details/42459595特征矩的知识在概率论和数理统计中有介绍,空间矩的方法在图像应用中比较广泛,包括零阶矩求面积、一阶矩确定重心、二阶矩确定主方向、二阶矩和三阶矩可以推导出七个不变矩Hu不变矩,不变矩具有旋转,平移、缩放等不变性,因此在工业应用和模式识别中得到广泛的应用。目标物体灰度函
参考 http://blog.csdn.net/yang6464158/article/details/42459595
特征矩的知识在概率论和数理统计中有介绍,空间矩的方法在图像应用中比较广泛,包括零阶矩求面积、一阶矩确定重心、二阶矩确定主方向、二阶矩和三阶矩可以推导出七个不变矩Hu不变矩,不变矩具有旋转,平移、缩放等不变性,因此在工业应用和模式识别中得到广泛的应用。
目标物体灰度函数特征矩的公式定义如下:
如果是二值图像,那么f(x,y)就变成
在OpenCV中,可以很方便的计算多边形区域的3阶特征矩,opencv中的矩主要包括以下几种:空间矩,中心矩和中心归一化矩。
class Moments { public: ...... // 空间矩 double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;// 中心矩double mu20, mu11, mu02, mu30, mu21, mu12, mu03;// 中心归一化矩 double nu20, nu11, nu02, nu30, nu21, nu12, nu03; }空间矩的公式为:
可以知道,对于01二值化的图像,m00即为轮廓的面积。中心矩的公式为:
其中:
归一化的中心矩公式为:
参考于 链接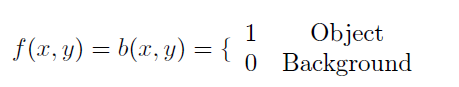
二阶中心距,也叫作方差,它告诉我们一个随机变量在它均值附近波动的大小,方差越大,波动性越大。方差也相当于机械运动中以重心为转轴的转动惯量。(The moment of inertia.)
三阶中心距告诉我们一个随机密度函数向左或向右偏斜的程度。
在均值不为零的情况下,原点距只有纯数学意义。
A2,二阶矩就是 E(X^2)即样本平方均值 ,具体说来就是 A2=(西格玛Xi^2)/n-----(2)
Ak,K阶矩就是 E(X^k)即样本K次方的均值,具体说来就是 Ak=(西格玛Xi^k)/n,-----(3)
不变矩的物理含义:
如果把图像看成是一块质量密度不均匀的薄板,其图像的灰度分布函数f(x,y)就是薄板的密度分布函数,则其各阶矩有着不同的含义,如零阶矩表示它的总质量;一阶矩表示它的质心;二阶矩又叫惯性矩,表示图像的大小和方向。事实上,如果仅考虑阶次为2的矩集,则原始图像等同于一个具有确定的大小、方向和离心率,以图像质心为中心且具有恒定辐射率的椭圆。由三阶矩以下矩构成的七个矩不变量具有平移、旋转和尺度不变性等等。当密度分布函数发生改变时,图像的实质没有改变,仍然可以看做一个薄板,只是密度分布有所改变。虽然此时各阶矩的值可能发生变化,但由各阶矩计算出的不变矩仍具有平移、旋转和尺度不变性。通过这个思想,可对图像进行简化处理,保留最能反映目标特性的信息,再用简化后的图像计算不变矩特征,可减少计算量。
研究表明,只有基于二阶矩的不变矩对二维物体的描述才是真正的与旋转、平移和尺度无关的。较高阶的矩对于成像过程中的误差,微小的变形等因素非常敏感,所以相应的不变矩基本上不能用于有效的物体识别。即使是基于二阶矩的不变矩也只能用来识别外形相差特别大的物理,否则他们的不变矩会因为很相似而不能识别。
在OpenCV中,还可以很方便的得到Hu不变距,Hu不变矩在图像旋转、缩放、平移等操作后,仍能保持矩的不变性,所以有时候用Hu不变距更能识别图像的特征。
1、在数学领域,矩 非常的常见
2、在计算机视觉中,使用2维离散形式的矩计算方法
3、使用矩,可以计算物体的面积,物体的质心等。
4、中心矩的计算方法是:某个矩除以0阶矩
5、高阶矩具有旋转不变性,尺度不变性,变换不变性等。
我们很熟悉概率论中的一阶矩二阶矩高阶矩,但是很多人可能和我一样,不明白图像中矩是拿来干嘛的。
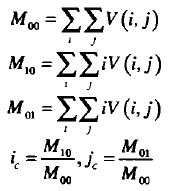
其中M00即零阶矩
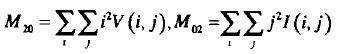
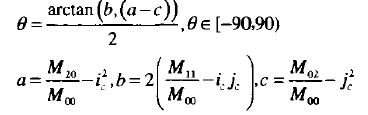
OpenCV代码如下所示:
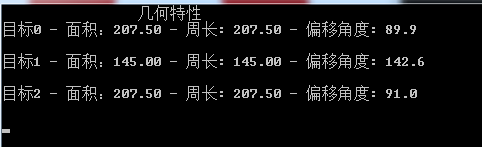
结果如下:
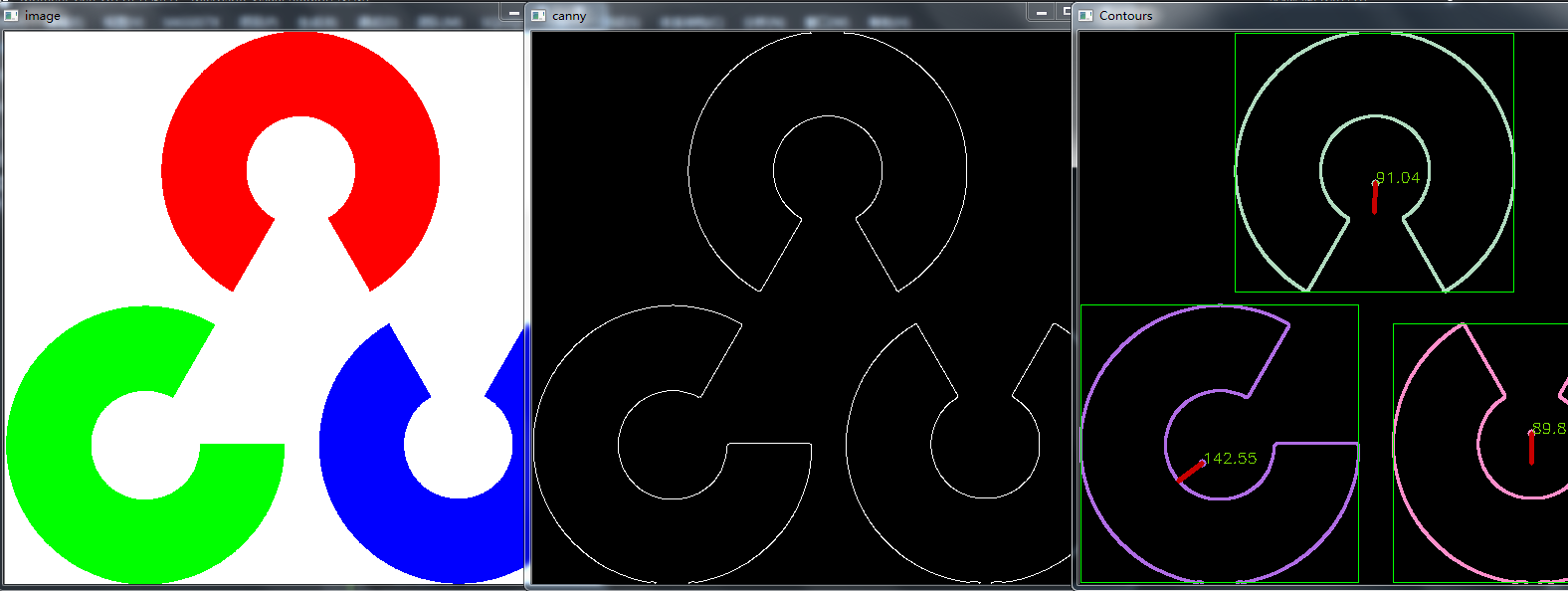
计算得到的第二个目标物面积和周长明显不正确,具体原因有待查找
矩、中心矩、质心、patch方向
author@jason_ql
http://blog.csdn.net/lql0716
1、几何矩理论
1.1 矩与数学期望
- 数学期望
定义(一维离散):设 X∈[a,b] ,密度为 f(x) ,数学期望为:
E(X)=∑i=1∞xiP(xi)
定义(一维连续):设 X 为连续型随机变量,其概率密度为 f(x) ,则X的数学期望为:
E(X)=∫+∞−∞xf(x)dx注:假定广义积分绝对收敛,即 ∫+∞−∞|x|f(x)dx 存在
定义(二维离散):对于离散变量 (X,Y) 的 P(xi,yi) , PX(xi)=∑jP(xi,yj) 期望为:
E(X)=∑ixiPX(xi)=∑j∑ixiP(xi,yj)
E(Y)=∑jyjPY(yj)=∑j∑iyjP(xi,yj)
定义(二维连续):连续变量 (X,Y) 的 f(x,y) :
fX(x)=∫+∞−∞f(x,y)dy
E(X)=∫+∞−∞xfX(x)dx=∫+∞−∞x(∫+∞−∞f(x,y)dy)dx=∫+∞−∞∫+∞−∞xf(x,y)dxdy
E(Y)=∫+∞−∞yfY(y)dy=∫+∞−∞∫+∞−∞yf(x,y)dxdy
- 原点矩
定义1:设 X 是随机变量,则称 νk(X)=E(Xk) 为 X 的 k 阶原点矩。
若 X 是离散型随机变量,则:
νk(X)=∑ixkip(xi)若 X 是连续型随机变量,则:
νk(X)=∫+∞−∞xkf(x)dx
- 中心距
定义2:设 X 是随机变量,则称
μk(X)=E(X−E(X))k为 X 的 k 阶 中心距。若 X 是离散型随机变量,则:
μk(X)=∑i(xi−E(X))kp(xi)若 X 是连续型随机变量,则:
μk(X)=∫+∞−∞(x−E(X))kf(x)dx
- 原点矩与中心距
当中心距中的 E(X) 为0时,此时为 k 阶原点矩,即原点矩是中心距的特殊情况。
一阶原点矩就是数学期望,二阶中心距就是方差,在实际中常用低阶矩,高于四阶矩极少使用。
原点矩与中心距的关系式:
以上可对 μr 用组合数拆开得到。
1.2 图像的矩
把图像的像素看做密度函数 f(x,y) ,对该像素点求期望 E ,即是图像的矩(原点矩)。具体的求解过程参看下面第2节。
一般来说,一阶矩和零阶矩可以计算某个形状的重心,二阶矩可以计算形状的方向。
图像的矩主要表征了图像区域的几何特征,又称几何矩,由于具有旋转、平移、尺度等不变的特兴奋,所以又称为不变矩。
利用不变矩可以计算出物体的圆形度(物体形状和园的接近程度)、物体的矩形度(物体形状和矩形的接近程度)、物体的水平和垂直对称性、物体的主轴方向、扁度等。
-
原点矩:
mpq=∑x−1M∑y−1Nxpyqf(x,y) -
中心距:
μpq=∑x−1M∑y−1N(x−x0)p(y−y0)qf(x,y) -
归一化中心距:
ηpq=μpqμr00
其中 r=p+q+22,p+q=2,3,... -
一阶矩:
见下面第2节. -
二阶矩:
M20 和 M02 分别表示图像围绕通过重心的垂直和水平轴线的惯性矩。
M30 和 M03 可以度量图像对于垂直和水平轴线的对称性等。
物体形状的方向:
其中:
根据一阶矩的质心 C=(M10M00,M01M00) 有
2、质心原理
在图像处理中,一阶矩与形状有关,二阶矩显示曲线围绕直线平均值到扩展程度,三阶矩是关于平均值到对称性到测量.由二阶矩和三阶矩可以导出一组共7个不变矩.而不变矩是图像到统计特性,满足平移,伸缩,旋转均不变到不变性.
-
moments of a patch(矩):
mpq=∑x=−r,y=−rrxpyqI(x,y)(1) -
角点为中心:
m00=∑x=−r,y=−rrx0y0I(x,y)=∑x=−r,y=−rrI(x,y)(1-1) -
一阶矩 m01 :
m01=∑x=−r,y=−rrx0y1I(x,y)=∑x=−r,y=−rry∗I(x,y)(1-2) -
一阶矩 m10 :
m10=∑x=−r,y=−rrx1y0I(x,y)=∑x=−r,y=−rrx∗I(x,y)(1-3) -
centroid(质心,亦可称为重心):
C=(m10m00,m01m00)(2)
计算质心的优势:对噪声不敏感。当有外部噪声干扰时,计算出的质心不会偏离太大。从数学的角度来看,这种方法是计算一个连通域的质心(或一个团块儿blob的质心)。 -
构造一个向量 OC−→− ,从角点中心 O 到质心 C 。
-
orientation of patch(方向):
θ=atan2(m01,m10)(3)
建立以角点为圆心的坐标系,如图
在图中, P 为角点,园内为取点区域,每个方格代表一个像素。
则质心 Q 可根据式(2)求得。
3、中心距函数moments()
Calculates all of the moments up to the third order of a polygon or rasterized shape.
C++: Moments moments(InputArray array, bool binaryImage=false )
Python: cv2.moments(array[, binaryImage]) → retval
C: void cvMoments(const CvArr* arr, CvMoments* moments, int binary=0 )
Python: cv.Moments(arr, binary=0) → moments
Parameters:
array– Raster image (single-channel, 8-bit or floating-point 2D array) or an array ( 1 \times N or N \times 1 ) of 2D points (Point or Point2f ).binaryImage– If it is true, all non-zero image pixels are treated as 1’s. The parameter is used for images only.moments– Output moments.
- The function computes moments, up to the 3rd order, of a vector shape or a rasterized shape. The results are returned in the structure Moments defined as:
4、中心矩示例代码
- opencv2.4.13
4.1 C++版代码
效果图:
部分打印结果:
4.2 Python版代码
原图:
效果图:
5、Hu矩HuMoments()
原点矩:
中心距:
归一化中心距:
其中 r=p+q+22,p+q=2,3,...
当图像变化时, mpq 也变化,而 μpq 具有平移不变形,但对旋转依然敏感。如果用归一化中心距,则可以保持平移不变性、伸缩不变性。
Hu矩利用二阶、三阶中心距构造了7个不变矩,它们在连续图像条件下可保持平移、旋转、伸缩不变,公式如下:
M1=η20+η02
M2=(η20−η02)2+4η211
M3=(η30−3η12)2+(3η21−η03)2
M4=(η30+η12)2+(η21+η03)2
M5=(η30−3η12)(η30+η12)((η30+η12)2−3(η21+η03)2)+(3η21−η03)(η21+η03)(3(η30+η12)2−(η21+η03)2)
M6=(η20−η02)((η30+η12)2−(η21+η03)2)+4η11(η30+η12)(η21+η03)
M7=(3η21−η03)(η30+η12)((η30+η12)2−3(η21+η03)2)−(η30−3η12)(η21+η03)(3(η30+η12)2−(η21+η03)2)
以下公式为官方文档的公式: 
在对图片识别过程中,只有 M1 和 M2 不变性保持的比较好,其他几个不变矩带来的误差比较大,有学者认为只有基于二阶矩的不变矩对二维物体的描述才真正具有旋转,缩放,平移不变性( M1 和 M2 均为二阶矩构成).
Hu矩的优势:速度快
Hu矩的劣势:识别率低
Hu矩一般用来识别图像中大的物体,对物体的形状描述得比较好,图像的纹理特征不能太复杂,如识别水果形状或车牌字符的效果较好.
- 参考:
1、图像的几何矩浅析
2、opencv官方文档-moments()
3、形状描述与识别
4、第三章 二值图像分
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容





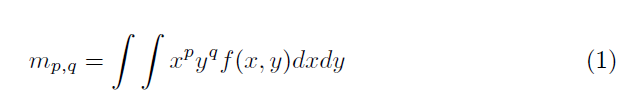














所有评论(0)