深度学习算法实践11---卷积神经网络(CNN)之卷积操作
卷积神经网络(CNN)主要特性有:稀疏连接和权值共享、卷积操作、池化。在前一篇博文中我们已经讨论了稀疏连接和权值共享,在本篇博文中,我们将介绍卷积操作和池化。正是由于对图像进行卷积操作,卷积神经网络才得以其名,可见卷积操作是其核心。在这篇博文中,我们将讨论卷积操作的实现其及物理含义。
卷积神经网络(CNN)主要特性有:稀疏连接和权值共享、卷积操作、池化。在前一篇博文中我们已经讨论了稀疏连接和权值共享,在本篇博文中,我们将介绍卷积操作和池化。正是由于对图像进行卷积操作,卷积神经网络才得以其名,可见卷积操作是其核心。在这篇博文中,我们将讨论卷积操作的实现其及物理含义。
首先,我们来了解一下卷积概念。对于一维信号,卷积定义为:
 式1
式1
而我们要处理的图像信号,是二维信号,卷积定义为:
 式2
式2
我们假设输入层以3*3为接收域,则其上层特征图也应该是3*3。
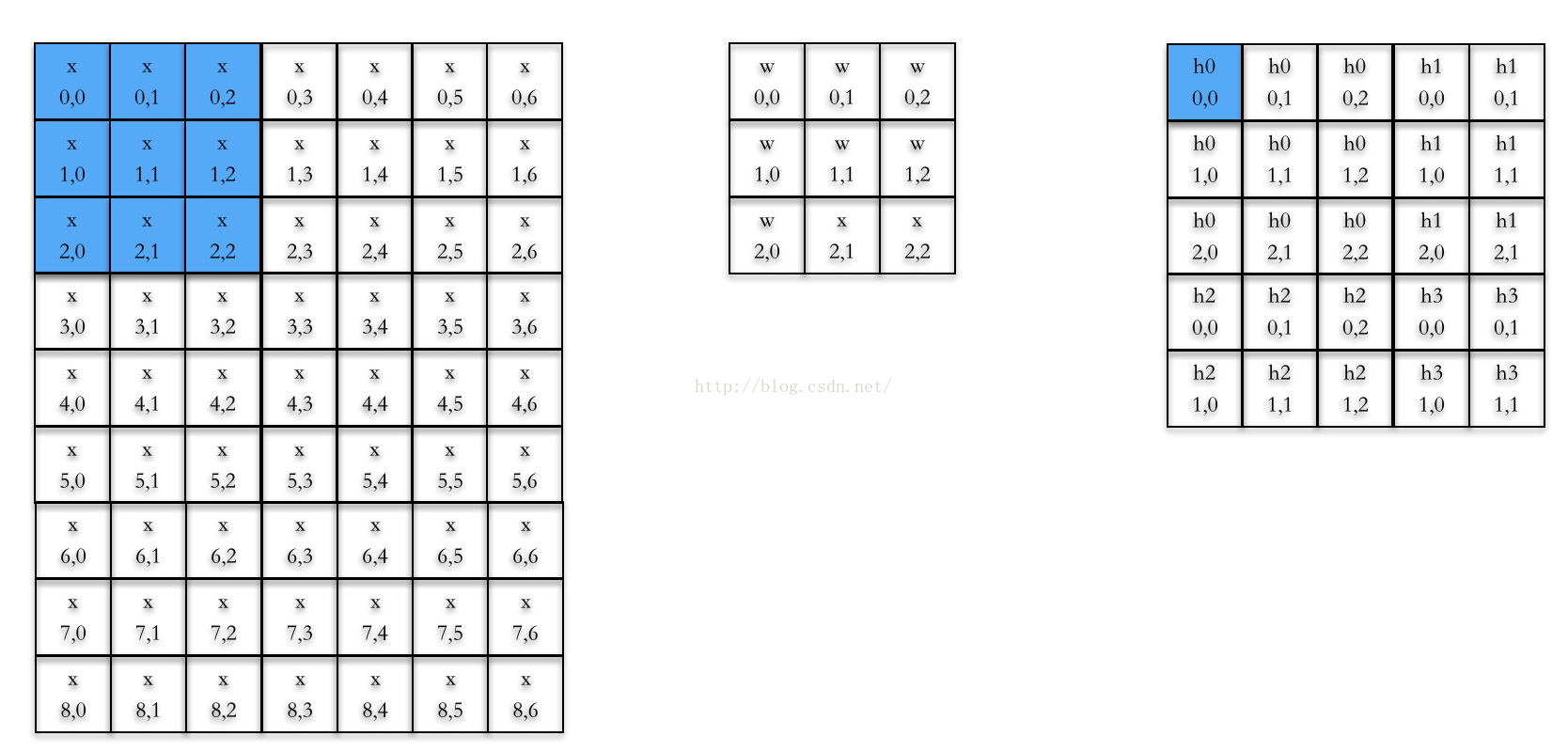
如下图所示,我们想要求出上一层第k个特征图(3*3),对其中每个节点i,j的值可以用如下公式求出:
 式3
式3
在上图中,我们需要求出上一层第0个特征图(0,0)点处神经元的输出值,则可知上式的k=0, i=0, j=0,具体列出式子为:
 式4
式4
由上图可知,这里的卷积就是将权值矩阵与图像进行卷积操作,将结果加上上一层对应位置神经元的Bias后再进行一个非线性变换,这里用的是双曲正切函数,即可求出上一层特征图对应位置的神经元输出。
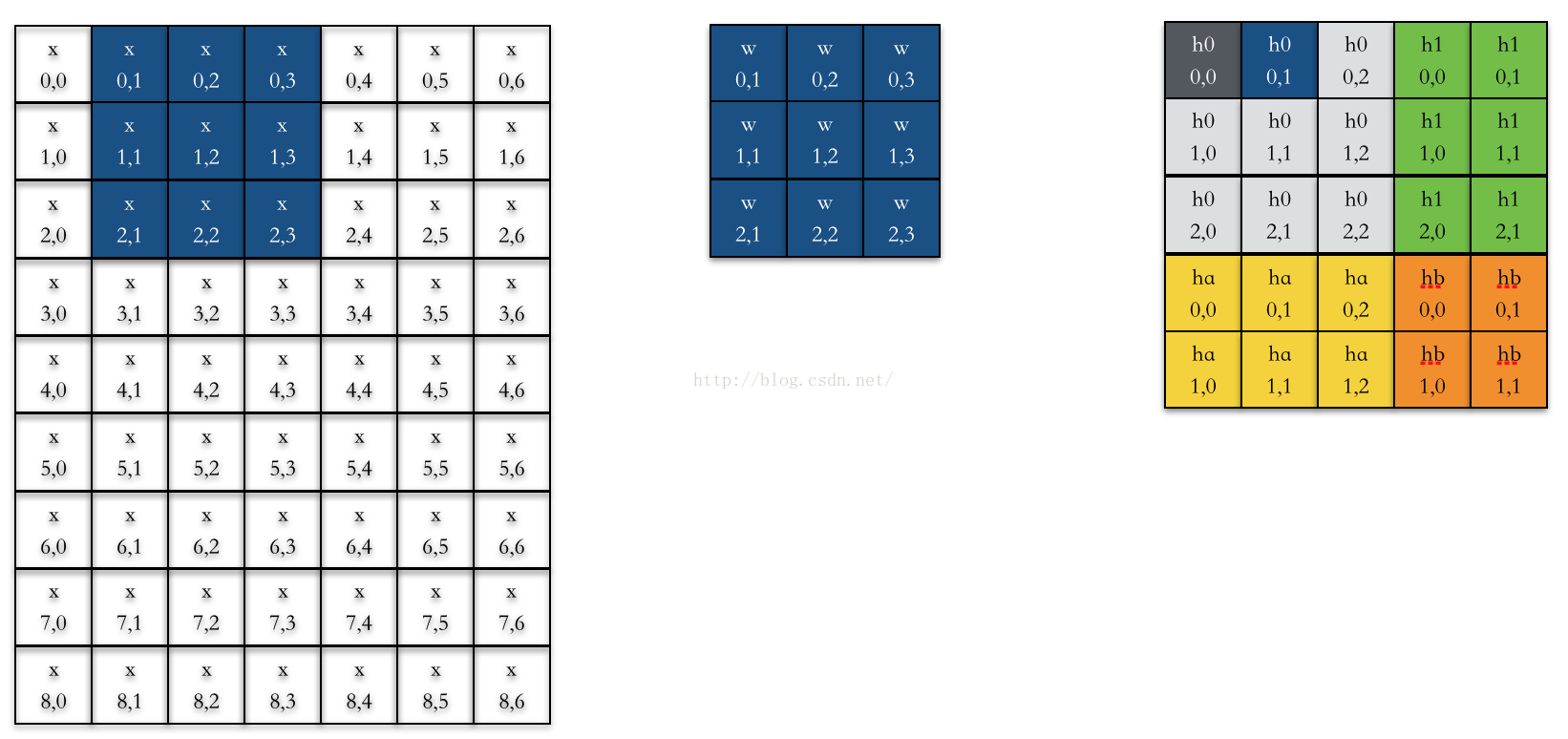
下面来求下一层中第0个特征图中(0,1)位置的神经元输出,如下图所示:
代入式3的公式,可以得出如下的
 式5
式5
有了上述的理论基础,让我们看一下,我们对一个原始图像做卷积操作会出现什么结果,在下面的程序中,我们定义图像输入层有3个特征图,上一层有2个特征图,特征图的尺寸为9*9,我们将做完卷积操作后的图像和之前的图像一并显示出来:
import theano
from theano import tensor as T
from theano.tensor.nnet import conv2d
import numpy
from matplotlib import pylab
from PIL import Image
def conv_wky():
rng = numpy.random.RandomState(23455)
input = T.tensor4(name='input')
w_shp = (2, 3, 9, 9)
w_bound = numpy.sqrt(3 * 9 * 9)
W = theano.shared( numpy.asarray(
rng.uniform(
low=-1.0 / w_bound,
high=1.0 / w_bound,
size=w_shp),
dtype=input.dtype), name ='W')
b_shp = (2,)
b = theano.shared(numpy.asarray(
rng.uniform(low=-.5, high=.5, size=b_shp),
dtype=input.dtype), name ='b')
conv_out = conv2d(input, W)
output = T.nnet.sigmoid(conv_out + b.dimshuffle('x', 0, 'x', 'x'))
return theano.function([input], output)
def do_conv():
f = conv_wky()
img = Image.open(open('3wolfmoon.jpg', 'rb'))
img = numpy.asarray(img, dtype='float64') / 256.
img_ = img.transpose(2, 0, 1).reshape(1, 3, 639, 516)
filtered_img = f(img_)
pylab.subplot(1, 3, 1); pylab.axis('off'); pylab.imshow(img)
pylab.gray()
pylab.subplot(1, 3, 2); pylab.axis('off'); pylab.imshow(filtered_img[0, 0, :, :])
pylab.subplot(1, 3, 3); pylab.axis('off'); pylab.imshow(filtered_img[0, 1, :, :])
pylab.show()
if __name__ == '__main__':
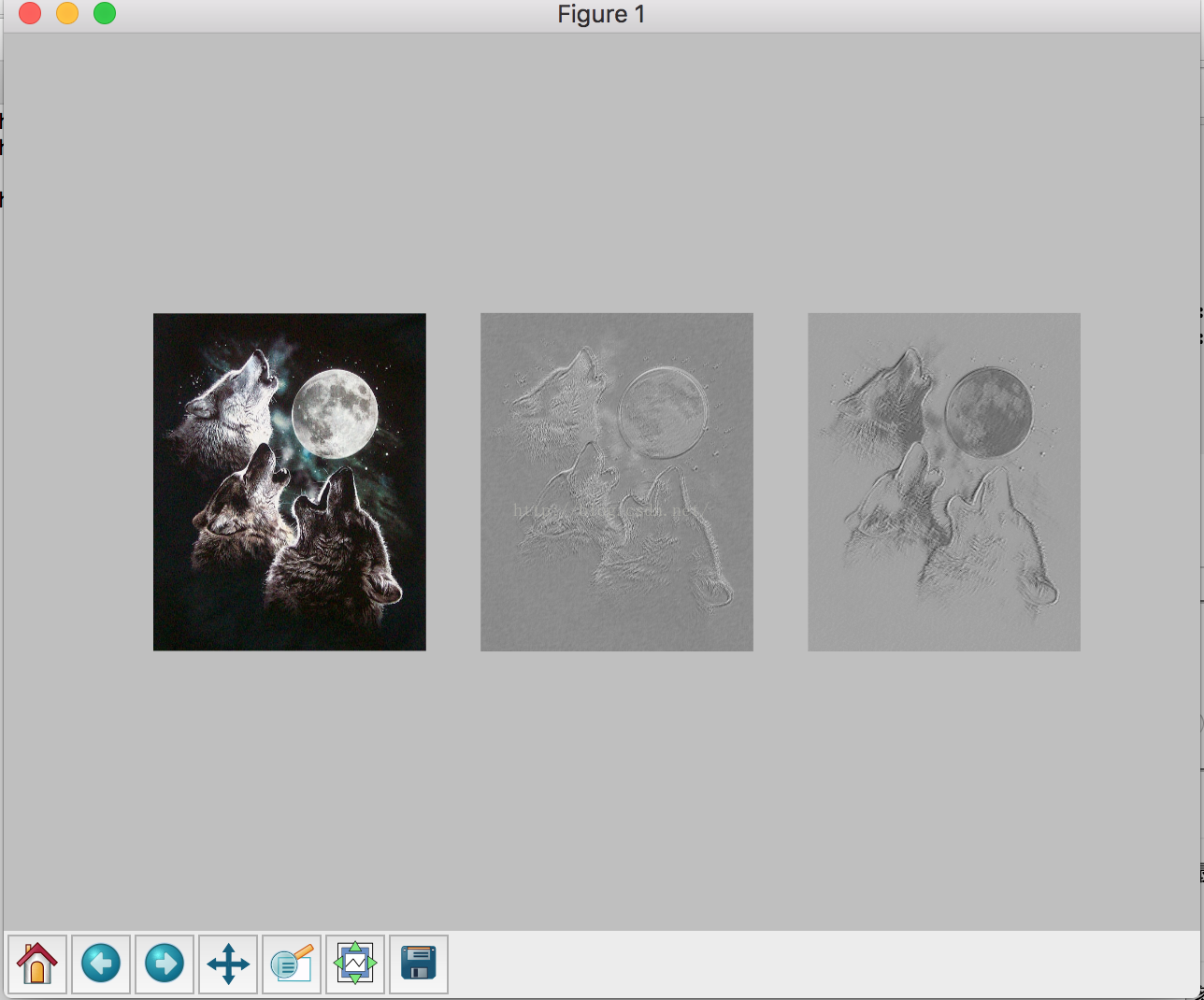
do_conv()结果如下所示:
如图所示,可以看出,对于图像进行一次卷积操作,相当于识别出了图像的边缘,我们知道,识别边缘是图像处理的基础操作,因此可以看出卷积操作是有其物理含义的。
我们知道怎么定义卷积操作之后,我们就可以开始实现卷积神经网络(CNN)了。在下一篇博文,我们将讨论怎样使用卷积神经网络(CNN)将MNIST手写数字识别的错误率降低到1%以内,这甚至超过了人类的识别率,足以看到卷积神经网络的巨大威力。
更多推荐
 已为社区贡献33条内容
已为社区贡献33条内容














所有评论(0)