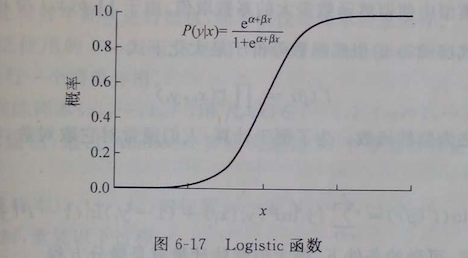
在有些模式识别问题中，如癌症病人的诊断，一个细胞是否是癌细胞，这种问题不能简单的用线性回归来研究特征与分类之间的关系。大多数情况中，某一特征对一个对象事物的影响是这样：在某一段范围内，可能属于一个类别，但是在下一个范围内又可能属于另一个类别，然后在下下一个范围可能又不同类，像这种比例渐进式的影响关系很难用一个模型假设来表达，该如何下手呢？要知道虽然类别与特征之间没有一个明确可建立的关系表达，但是归属于某一个类别（如第一类）的概率却是跟特征有一定关系的，如图：

从函数形式和曲线上看，它跟Sigmoid函数长得很像；

通常我们说一种病的患病几率多少多少，这里的“几率”其实就是患病的概率与不患病概率的比值，而这种患病概率满足上述Logistic函数，因此几率用如下公式表示就是：

取其对数：

                  (1)

上述公式（1）被称为P(y|x)的logit函数，而y与x的这种关系模型称作Logistic模型，β反映了当x增加一个单位，样本属于某一类的几率在对数尺度上增加的幅度。

同线性回归一样，上述特征既可以是连续的，也可以是离散的。

推广到多元，公式（1）变成：

                        (2)

上述模型就构成了多元的逻辑回归模型，描述了样本归属于某一类的概率与特征之间的关系，下面我们来学习上式中的回归参数β；

对于逻辑回归，其基本的学习算法是最大似然法，就是求出是似然函数最大化的参数，下面用简单的两类问题来阐明；

训练样本：独立，数量为n个；其中n1个属于第一类（y=1），剩下属于第二类（y=2）；

观察每一个样本出现的概率：

                  (3)

其中，为样本的总体概率密度；

于是得到其似然函数：

观察上式可以发现，对求积跟逻辑回归模型中的所求参数无关，因此上式可简化为：

                        (4)

称之为似然函数，要对其最大化；

取其对数，得到对数似然函数：

                              (5)

根据线性代数相关知识，如果上述似然函数连续且可微，那么最大似然估计量满足：

     ，说白了就是求导；

另外，根据公式（2）知道，如果一个样本属于第一类时的概率为：

                      （6）

将其代入对数似然函数（公式（5））中，有：

（一元）

   (多元)

再次把公式（6）代入到上面两个公式中会得到一组关于β的非线性方程组，但是很遗憾，这种直接求导等于0的方式最后得到的一组关于β的非线性方程组无法求解，所以同线性回归一样使用梯度下降来求解，关于梯度下降的求解我就不细说了，因为前面的文章（如感知器）中有讲到过如何下降，在这里只说一点需要注意的地方，就是它跟线性回归里的求解方法有一个很大的不同，线性回归里求的是各样本的残差平方和最小化，而逻辑回归里则是似然函数最大化，所以梯度下降的方向相反，前者是往梯度负方向，后者是梯度方向，千万要注意辣。。

           （6）

给出伪代码：

设置迭代用的β初始值，可设为1

do

{

      遍历样本数据集，计算梯度；

      按照公式（6）进行β更新；

}while（算法收敛）

输出β

关于学习率的选取，可参考线性回归一文中的选取方法；

当然，梯度下降也并非一种最优求解，因为极容易陷入局部最优，所以可以使用GD算法的改进版--随机梯度下降（SGD），它的出现是为了减轻GD中的遍历计算，主要思想是每次只用一个样本的梯度来更新回归系数。