目录

1、指数增长模型（Malthus人口模型）

【模型假设】

【符号说明】

【模型建立】

【参数估计】 

【误差原因分析】

【模型的优缺点】

1、优点

2、缺点

3、修正方案 

 2、阻滞增长人口模型（Logistic模型）

【模型假设】

【符号设置】

【模型建立】

1、构造模型

 2、关于Logistic模型的特别分析

2.1 人口速度增长最快点

2.2 Logistic模型曲线

【模型求解】

【参数估计】

---

下表1给出了近两个世纪美国人口统计表（单位：百万），建立数学模型并检验，最后用它预报2010年美国的人口。

年	1790	1800	1810	1820	1830	1840	1850	1860
人口	3.9	5.3	7.2	9.6	12.9	17.1	23.2	31.4
年	1870	1880	1890	1900	1910	1920	1930
人口	38.6	50.2	62.9	76.0	92.0	106.5	123.2
年	1940	1950	1960	1970	1980	1990	2000
人口	131.7	150.7	179.3	204.0	226.5	251.4	281.4

                                           表1 美国人口统计，单位：百万

1、指数增长模型（Malthus人口模型）

托马斯·罗伯特·马尔萨斯牧师(Thomas Robert Malthus，1766年2月13日-1834年12月23日)。英国教士、人口学家、经济学家。以其人口理论闻名于世。     在《人口论》(1798)中指出:人口按几何级数增长而生活资源只能按算术级数增长，所以不可避免地要导致饥馑、战争和疾病;呼吁采取果断措施，遏制人口出生率。其理论对李嘉图产生过影响 。

【模型假设】

1. 人口增长率为常数
2. 单位时间内人口的绝对增长与当前人口数量成正比
3. 人口总数随时间连续变化

【符号说明】

【模型建立】

 t时刻人口总量为x(t)，对一个地区或国家来说，x(t)数量很大，视为一个可微函数。 

  记初始时刻t=0时，人口总数为x0。根据假设（2），从t到t+Δt时间内，人口的增量正比于x(t)与Δt的乘积，即

令Δt→0，得到x(t)的微分方程【2.1】

变量分离容易求出【2.2】

【2.2】称为指数增长模型，也称Malthus人口模型。

【参数估计】 

为了更好利用表1的数据和线性拟合参数，对【2】两边取对数，有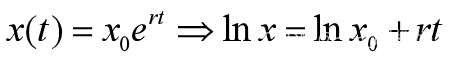

设y=lnx,a=lnx0,则有y=a+rt【3】

 这类模型的目的是为了预报预测，预测准不准确不是模型本身可以完全决定的，需要用实际数据检验。所以，在数据拟合时，一般采用前2/3的数据来拟合参数（自找导师监督学习），用后1/3的数据来检验模型的可用性。如果数据本身较少，也说明可获取的信息太少，模型的可信度本来就低。

 用前12个数据，用matlab软件做直线拟合

clear
A=xlsread('d:\Arenkou.xlsx');
A=A';
t=A(:,1);x=A(:,2);
t1=t(1:12);y=log(x(1:12));
[b,bt,r,rt,st]=regress(y,[ones(length(y),1),t1]);
x0=exp(b(1));r=b(2);

得到预报公式为： 

【4】

图2是前12个年份的理论值（线）与实际值（*）的对比。可以看出，这个模型基本上能够描述19世界以前美国人口增长。 这和假设（1），即人口增长率是常数基本吻合。

                        图2  指数增长模型拟合图 （1790-1900）

 图3是全部年份的理论值（线）与实际值（*）的对比。从图可以看出，进入20世纪后，美国人口明增长变慢了，模型不再适应。 

                              图3 指数增长模型拟合图（1790-2000） 

【误差原因分析】

利用差商的形式来定义增长率，即【5】

将表1中数据代入【5】，得到r(k),并绘制如图4。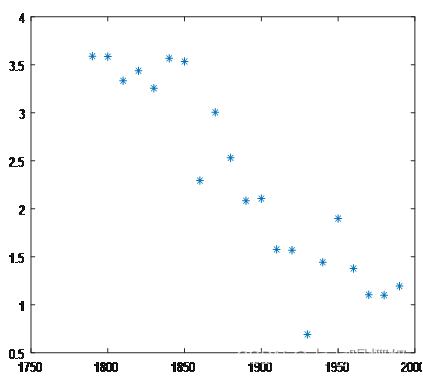 

                              图4 时间-增长率散点图

由图4可以看出，虽然增长率是摆动的，但随着人口增长，增长率有明显的下降趋势。也可以看到，1930年左右增长率特别小（29年经济大萧条所致）。 

【模型的优缺点】

1、优点

1. 模型简单，易于理解和计算
2. 从第一张图可以看出，Malthus人口模型在短期内拟合较好，短期预测误差不是很大

2、缺点

1. 从第二张图可以看出，Malthus模型不能做中长期的预测，误差较大
2. 从看，这根本不可能，说明模型假设存在致命的缺陷。

3、修正方案 

把增长率是常数修改为增长率随人口增加而降低。 

 2、阻滞增长人口模型（Logistic模型）

由图4的结论知道，增长率会随着人口增长而下降，其真实的原因是自然资源、环境条件等人类赖以生存的条件阻滞着人口增长，随着人口增加，阻滞作用越大。

【模型假设】

1. 人口数随时间连续变化
2. 一定环境下人口总数有个上限，即最大人口数xm
3. 单位时间内人口的增长量等于当前人口量×当前人口增长率
4. 某时刻的人口增长率是该时刻人口数量的线性减函数
5. 人口达到最大负荷时，增长率为0

【符号设置】

【模型建立】

1、构造模型

增长率随人口增加而减少，不妨设为r(x),是x的减函数，最简单直接的表达式就是线性函数

【6】

其中r称为固有增长率，当x=0时的最大增长率，s是阻滞系数，不妨设x=xm时，即人口达到最大负荷时，增长率为0，即【7】

将【7】代入【6】，则有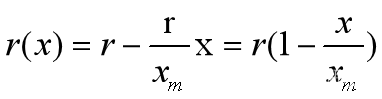【8】

根据假设【3】，有【9】

在【9】中，dx/dt表示人口的实际增长速度为两部分，rx随人口增加而增加，(1-x/xm)随人口增加而减少，即人口增长是两个因子共同作用的结果。【9】所反映的增长模型称为阻滞增长模型，也称Logistic模型。

 凡是资源有限的生物总群模型，大多可以用这个模型去描述总群数量的变化规律；很多产品的生产模型、营销模型也满足这个规律。

 2、关于Logistic模型的特别分析

2.1 人口速度增长最快点

既然人口增长速度（变量）随人口数量（变量）增加而减少，由两边对x求导，得

由此可见，在x<xm/2时单调递增；在x>xm/2时单调递减，x=xm/2时，人口变化速度达到最大。如图5所示。

                     图5 Logistic模型      dx/dt-x曲线

2.2 Logistic模型曲线

由知道，人口数量x(t)是时间t的单调递增函数，又由于

所以有

不妨设x(t0)=xm/2，则t<t0时x(t)是凹函数；t>t0时x(t)是凸函数。如图6所示。

                       图6 Logistic模型x-t曲线（又称s型曲线）

【模型求解】

【9】

【9】是变量分离的微分方程，求解得到特解为

【10】

由【10】的表达式可以得到如下结论：

（1）

（2）

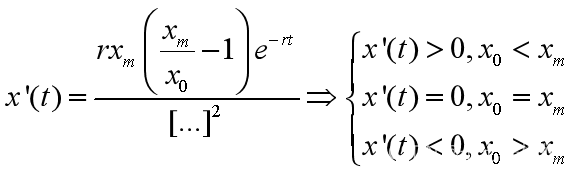
 将x0的三种情况所得的曲线绘制在同一坐标系下，结果如图7所示

                     图7 人口曲线随初值x0不同而不同的示意图

【参数估计】

【10】

表1的原始数据中t较大，又是指数函数的自变量，容易造成极端计算，故作变换后变成如下模型

【11】

利用表1的前21个数据，在matlab里调用最小二乘曲线拟合，得到xm=397.2117;x0=7.1100;r=0.2255

预测2000年美国人口值为=268.08（百万）

预测相对误差达到4.63%。

图8 前21数据的Logistic模型 的x-t拟合                          图9 去掉前9个数据的Logistic模型的x-t拟合

 = 277.9145(按图9的预测）

预测相对误差1.23%，优于图8的预测。从图9可以看出，前期误差较大。这也说明，生物种群当前数据受到近期历史影响大，远期影响小。