“约瑟夫环”问题的四种方法及详解注释(c++实现)
·
Ⅰ.故事背景
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。 [1]
17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15 个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。
Ⅱ.问题描述
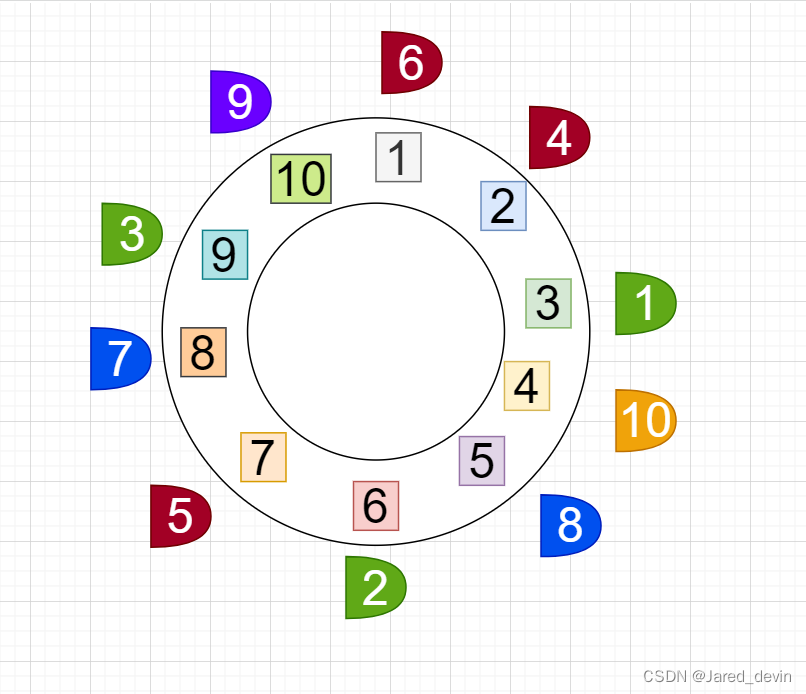
算法举例抽象为:已知 n 个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。第一个人开始报数,数到 k 的那个人出圈;他的下一个人又从 1 开始报数,数到 k 的那个人又出圈;依此规律重复下去,直到剩余最后一个胜利者。

(图片以n=10,k=3为例)
Ⅲ.代码实现
一.数组
#include<iostream>
#include<map>
using namespace std;
map<int,int> mp;
void Joseph_ring(int n, int k)
{
for (int i = 1; i <= n; i++)
{
mp[i] = 0;//将1——n对应的value值赋值为0
}
int cnt1 = 0;//记录删除个数
int cnt2 = 0;//统计有几个没出局的人报了号
int j = 0;
while (cnt1 < n)//只有value=0才报数
{
j++;
if (j > n)j = 1;//过头重置为1
if (!mp[j])
{
cnt2++;
if (cnt2 == k)//当前这个人出局
{
mp[j] = 1;//标记为1
cout << j << " ";
cnt1++;
cnt2 = 0;//归0
}
}
}
}
int main()
{
int n, k;
cin >> n >> k;
Joseph_ring(n, k);
return 0;
}
二.递归方法

(图片来自b站麦克老师)
#include<iostream>
using namespace std;
int ysf(int n, int k, int i)//本函数是index=0开始(上图有)
{
if (i == 1)
return (n+k-1) % n;
if (i != 1)
return (ysf(n - 1, k, i - 1) + k) % n;//即为去掉前面的人构成的新环的第i-1次
}
int main()
{
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cout << ysf(n, k, i)+1 << " ";//加1统一index=1开始
}
}
三.循环链表
#include<iostream>
#include<cstdlib>
using namespace std;
typedef struct node
{
int data;
struct node* next;
}Node;
int n, k;
void Joseph_ring(int n, int k)
{
//开始创建循环链表
Node* head = NULL, * p = NULL, * r = NULL;//搞三个指针
head = (Node*)malloc(sizeof(Node));//为head头指针申请一片空间((Node*)为强制类型转换为结构体变量指针)
head->data = 1;
head->next = NULL;
p = head;//创建循环链表用,此时p和head指向头结点
for (int i = 2; i <= n; i++)//创建剩下的n-1个结点(尾插法顺序插入)
{
r = (Node*)malloc(sizeof(Node));
r->data = i;
r->next = NULL;
p->next = r;
p = r;
}
p->next = head;//首尾相接
p = head;//恢复初始状态
while (p->next != p)//结束条件是只剩下最后一个(当然用cnt计数也可以)
{
for (int i = 1; i < k; i++)
{
r = p;//用r保存该删结点的上一个结点
p = p->next;
}
//循环结束后p指针的位置是该删结点的位置
cout << p->data << " ";
r->next = p->next;
p = p->next;
}
//whlie循环结束后还剩最后一个结点要输出
cout << p->data;
}
int main()
{
cin >> n >> k;
Joseph_ring(n,k);
return 0;
}
四.队列
#include<iostream>
#include<queue>
using namespace std;
queue<int> res;
int n, k;
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
res.push(i);
}
int cnt = 0;
while (!res.empty())
{
for (int i = 1; i <= k - 1; i++)//执行k-1次
{
res.push(res.front());//将队首元素放队尾去
res.pop();
}
//循环结束后输出队首元素
cout << res.front() << " ";
res.pop();//拖出去斩了
}
return 0;
}
阅读全文
AI总结
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容










所有评论(0)