逆合成孔径雷达ISAR成像&压缩感知ISAR成像

该内容采用经典的OMP算法，结合ISAR成像算法，对典型的空间目标散射点模型，利用傅里叶变换基或者离散余弦变换变换基实现ISAR压缩感知成像，并对比了不同回波稀疏度情况下的ISAR图像的图像熵。

UltraMan之神

3055人浏览 · 2023-08-31 16:04:34

UltraMan之神 · 2023-08-31 16:04:34 发布

1、压缩感知理论

压缩感知是指利用信号在某个域的稀疏性，获取比传统的奈奎斯特采样定律要求更少的测量数据，通过非线性的优化计算方法进行求解，从而高精度地恢复出原始信号。压缩感知要求信号是稀疏的或者是可压缩的，事实上，大多数自然信号都不是直接可压缩的，因此这些信号并不能直接进行降维再重构。但是，随着多尺度几何变换的兴起，很多信号在某些变换基域表现出稀疏特性，这为信号的稀疏表示提供了新的思路。不失一般性，考虑一个长度为N的一维实数信号x，信号x可投影到某个变换空间，该空间的基矩阵为N*N维的 $\Phi$ ，其列是由基向量 $\Phi _i$ 构成的， $\Phi$ 称为稀疏变换矩阵；加权系数向量为 $\alpha =[\alpha_1,\alpha_2,...,\alpha_n,...,\alpha_N]^T$ ，其中，绝大多数加权系数 $\alpha_n$ 都很小，只有K个系数远远大于其他系数，则称信号x是K稀疏的。该过程图1所示。

图1 信号的稀疏变换过程

压缩感知主要是为了减少测量数据个数，其降维观测过程如图2所示。通过一个与稀疏变换矩阵极度不相关的M*N(M<<N)维的测量矩阵对原始信号进行降维观测，可以表示为：

其中， $\Theta =\Phi \Psi$ 称为传感矩阵。当 $\Theta$ 矩阵满足RIP特性时，上述欠定性问题可以转化为 $l_0$ 范数的最优化问题，即：

上述最小 $l_0$ 范数模型可以通过贪婪算法、凸松弛算法以及组合算法这三类有效算法进行求解。

图2 信号的降维观测过程

2、基于压缩感知的雷达成像算法

在雷达成像中，稀疏性是最常见的先验信息。空间目标可以看作由一些孤立的散射点构成，ISAR图像也具有明显的稀疏特性，正好契合压缩感知算法的前提要求。此时，雷达成像问题转化为一个信号的稀疏表示问题。

当相控阵雷达对空间目标进行全孔径观测时，记雷达在一个成像调度间隔内需发射脉冲串个数为： $N_k=PRF*T$ ( $PRF$ 为脉冲重复频率， $T$ 为观测时间)，雷达接收到的信号可以表示为 $s(t,\tau _m)$ ，其中, $t$ 是快时间， $\tau _m$ 为慢时间序列，m取值范围为 $1\sim N_k$ 。实际相控阵雷达由于其波束捷变性，可以灵活地对不同目标进行交替观测，充分发挥相控阵雷达的观测潜力。

针对相控阵雷达成像系统，为节约雷达的观测孔径资源，可以对目标采用稀疏孔径观测方式进行方位向的采样，即仅对可观测目标发射 $M_k(M_k< N_k)$ 个LFM信号。如图3所示。此时，雷达接收到的回波信号也是稀疏的，可以表示为 $s(t,\tau _m^,)$ ， $m^,$ 取值为 $1 \sim M_k$ 。

图3 雷达稀疏观测示意图

在ISAR图像中，目标散射点分布可以认为是稀疏的。结合CS理论框架，可以把全孔径的单个距离单元作为原始信号，雷达接收到的稀疏回波作为信号的降维观测值。因此，可以选择逆傅里叶变换矩阵作为信号的稀疏变换矩阵，然后根据稀疏孔径的分布形式，设计一个维度为 $M_k* N_k$ 的部分随机单位矩阵作为压缩感知的观测矩阵。该观测矩阵可以表示为：

在很多文献中已指出：由逆傅里叶变换矩阵组成的稀疏变换矩阵和由部分随机单位矩阵组成的降维观测矩阵满足RIP性质（有限等距特性），当最低的采样数满足 $M_k*\geqslant c_1*K*ln(N_k)$ 时（ $c_1$ 为0.5~2的常数），可以通过压缩感知重构算法得到准确的方位向信息，从而得到空间目标的ISAR图像。

3、基于压缩感知的雷达ISAR成像实验

本文对典型的空间目标进行稀疏孔径ISAR成像实验，实验对象的光学图像以及对应散射点模型分别如图4与图5所示。

图4 空间目标的光学图像

图5 空间目标对应散射点模型

后续的实验主要探讨不同回波稀疏度情况下的目标雷达回波所形成的一维距离像HRRP以及成像结果，并通过图像熵来衡量目标ISAR图像质量，图像熵越小，代表图像质量越高，ISAR图像聚焦性能越好。

图6 全孔径HRRP 序列

图 7 全孔径ISAR成像结果

图8 数据率为75%的HRRP 序列

图 9 数据率为75%ISAR成像结果

图10 数据率为50%的HRRP 序列

图 11 数据率为50%ISAR成像结果

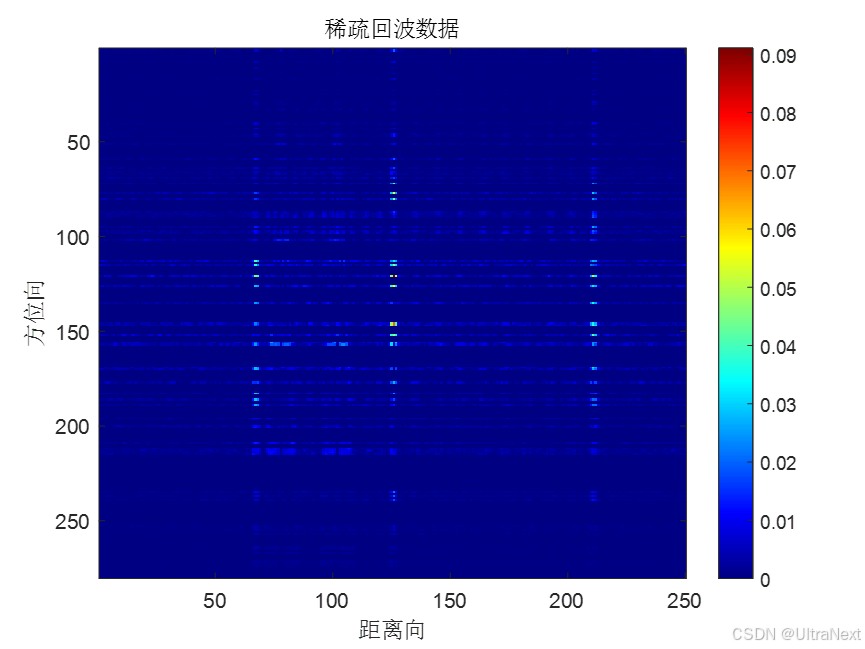
图12 数据率为25%的HRRP 序列

图 13 数据率为25%ISAR成像结果

4、结论

从上述对比实验中可以明显看出，随着数据率的减小，基于压缩感知的ISAR成像算法所得到的ISAR成像结果图像熵逐渐变大，成像质量有所下降。但是即便如此，该方法仍然是多目标同时成像技术的重要理论基础，只要合理地将不同的雷达孔径分配给不同的目标，就可以实现相控阵雷达的成像资源的有效调度。

部分代码如下：如有代码问题，请加V（UltraNextYJ）交流。

S(:,:,sp)=s;
%% 距离向压缩

for i=1:M
      temp=S(i,:,sp).*hamming(N)';
      S(i,:,sp)=-C/2/gama/cos(beta(sp))*fftshift(fft(temp));
end

%% 方位向加窗处理（在压缩感知回复之前进行加窗处理，提高恢复图像聚焦性能）

for j=1:N
    S(:,j,sp)=S(:,j,sp).*hamming(M);
end

%%  稀疏数据生成

% ==============数据选择矩阵=====================
vector_a = zeros(M,1); 
vector_b = randperm(M,floor((1-no_data_ratio)*M));  %随机n个100以内的数
vector_a(vector_b) = 1;
data_choose = diag(vector_a);

% ============= 对回波进行孔径数据选择=====================
S(:,:,sp) = data_choose*S(:,:,sp);
figure;
imagesc(abs(S(:,:,1)));
colormap jet
colorbar
xlabel('距离向');ylabel('方位向');
title('稀疏回波数据');

% =====================对方位向稀疏信号进行重构=====================
vector_b = sort(vector_b);
norm_length = length(vector_b);    %记录方位向数据正常的长度

%将正常数据重新组成矩阵
echos = S(:,:,sp);
echo_rank(1:norm_length,:) = echos(vector_b(:),:);

%根据数据选择矩阵来写观测矩阵
Phi(1:norm_length,:) = data_choose(vector_b(:),:);

echo_recovery = zeros(M,N);

for i = 1:N
      data = echo_rank(:,i);
      [hat_y] = CS_OMP_FunC(data,K,M,norm_length,Phi,choice_transform);
      echo_recovery(:,i) = fftshift(hat_y');
      waitbar(i/N,waiting);
end
S(:,:,sp) = echo_recovery;   %通过CS得到的二维像

点击阅读全文