ADC的ENOB(有效位数)计算公式的推导,以及其他相关参数的介绍
文章目录
对于ENOB的疑问
我最早的疑问来自于下面这个公式
E
N
O
B
=
S
I
N
A
D
[
d
B
]
−
1.76
6.02
ENOB=\frac{SINAD[dB] - 1.76}{6.02}
ENOB=6.02SINAD[dB]−1.76
这是一个SINAD(信号对噪声和失真的比值)与ENOB(有效位数)的转换式,我好奇这个式子是这么来的。
下文介绍了我对于这个公式的推导,以及ADC其他参数所代表含义发分析。
AC参数专业名词的解释
在分享这个式子之前我们先来对一些专有名词的定义进行一下总结(我一开始因为名称混淆迷糊了好久,必须要清楚各个名称的意思才能进行后面的推导)
参考文献:
《Analog Engineer’s Pocket Reference》
《揭开一个公式(SNR = 6.02N + 1.76dB)的神秘面纱, 以及为什么我们要予以关注》
SNR-信号噪声功率比
均方根信号与均方根噪声的比值
SNR也就是我们常说的信噪比,
S
N
R
=
20
×
l
o
g
(
M
a
x
R
M
S
S
i
g
n
a
l
R
M
S
N
o
i
s
e
)
=
10
×
l
o
g
(
P
s
i
g
n
a
l
P
n
o
i
s
e
)
\begin{aligned} SNR&= 20\times log(\frac {Max\quad RMS\quad Signal}{RMS\quad Noise}) \\ &=10\times log(\frac{P_{signal}}{P_{noise}}) \end{aligned}
SNR=20×log(RMSNoiseMaxRMSSignal)=10×log(PnoisePsignal)
M
a
x
R
M
S
S
i
g
n
a
l
Max\quad RMS\quad Signal
MaxRMSSignal 是 最大输入信号的均方根
R M S N o i s e RMS\quad Noise RMSNoise 是 噪声信号的均方根
P s i g n a l P_{signal} Psignal 是输入信号功率, P n o i s e P_{noise} Pnoise 是噪声功率(不包括任何谐波以及直流成分)
上面两式仅仅只是形式不同,在电路信号分析中是相互等效的(信噪比在声学中也有使用)
THD-总谐波失真
指的是基波信号的均方根值与其谐波(一般仅前5次谐波带入计算)的和方根的平均值之比
T
H
D
=
∑
n
=
0
∞
G
n
2
G
0
T
H
D
[
d
B
]
=
20
×
l
o
g
(
R
M
S
D
i
s
t
o
r
t
i
o
n
M
a
x
R
M
S
S
i
g
n
a
l
)
\begin{aligned} THD&=\frac{\sqrt{\displaystyle \sum^{\infin}_{n =0}G{^2 _n}}}{G_0} \\ THD[dB]&=20 \times log(\frac{RMS\quad Distortion}{{Max\quad RMS\quad Signal}}) \end{aligned}
THDTHD[dB]=G0n=0∑∞Gn2=20×log(MaxRMSSignalRMSDistortion)
R
M
S
D
i
s
t
o
r
t
i
o
n
RMS\quad Distortion
RMSDistortion 是 所有谐波分量的均方根之和
G 0 G_0 G0 是基波, G n G_n Gn 是第n次谐波
需要注意的是,THD中输入信号做分母
SINAD-信号对噪声和失真的比值
SINAD又叫信纳比,是输入信号和所有输出信号失真(包括谐波成分,不包括直流)的功率之比,
S
I
N
A
D
=
10
×
l
o
g
(
P
s
i
g
n
a
l
P
n
o
i
s
e
+
P
d
i
s
t
o
r
t
i
o
n
)
=
20
×
l
o
g
(
M
a
x
R
M
S
S
i
g
n
a
l
R
M
S
N
o
i
s
e
2
+
R
M
S
D
i
s
t
o
r
t
i
o
n
2
)
\begin{aligned} SINAD&=10 \times log(\frac{P_{signal}}{P_{noise}+P_{distortion}}) \\ &=20 \times log(\frac{Max\quad RMS\quad Signal}{\sqrt{{RMS\quad Noise}^2\quad+\quad{RMS\quad Distortion}^2}}) \end{aligned}
SINAD=10×log(Pnoise+PdistortionPsignal)=20×log(RMSNoise2+RMSDistortion2MaxRMSSignal)
P
d
i
s
t
o
r
t
i
o
n
P_{distortion}
Pdistortion 是失真信号功率(各次谐波功率之和)
从公式中可以看出,SINAD是SNR与THD的结合
各个AC参数的推导与关联
从DR开始计算
DR(ADC 的动态范围)其代表 ADC 可测量的输入信号等级范围,通俗来说就是最大可测量比最小可测量,通常以 [dB] 为单位。
这个参数是后面计算的基础。
D
R
[
d
B
]
=
20
×
l
o
g
(
m
a
x
R
M
S
a
m
p
l
i
t
u
d
e
m
i
n
R
M
S
a
m
p
l
i
t
u
d
e
)
DR[dB]=20 \times log(\frac {max \quad RMS \quad amplitude}{min \quad RMS \quad amplitude})
DR[dB]=20×log(minRMSamplitudemaxRMSamplitude)
m
a
x
R
M
S
a
m
p
l
i
t
u
d
e
max \quad RMS \quad amplitude
maxRMSamplitude 意为:最大均方根幅值
m i n R M S a m p l i t u d e min \quad RMS \quad amplitude minRMSamplitude 意为:最小均方根幅值
若输入信号为直流
直流信号的均方根幅值就是它本身的电压
所以
R
[
d
B
]
=
20
×
l
o
g
(
F
S
R
F
S
R
2
N
)
=
20
l
o
g
2
10
×
N
≈
6.02
N
R[dB]=20 \times log(\frac{FSR}{\frac {FSR} {2^N}}) = \frac {20}{log{_2}10} \times N \approx 6.02N
R[dB]=20×log(2NFSRFSR)=log21020×N≈6.02N
N
N
N 是ADC位数
F S R FSR FSR 是ADC最大量程
若输入信号为正弦信号
D
R
[
d
B
]
=
20
×
l
o
g
(
F
S
R
/
2
2
(
F
S
R
2
N
)
/
2
3
)
=
20
l
o
g
2
10
×
N
+
20
×
l
o
g
(
6
2
)
≈
6.02
N
+
1.76
\begin{aligned} DR[dB]&=20 \times log(\frac {FSR/2\sqrt2}{(\frac{FSR}{2^N})/ 2\sqrt3}) \\ &=\frac {20}{log{_2}10}\times N\quad + \quad 20 \times log(\frac{\sqrt6}{2}) \\ &\approx6.02N + 1.76 \end{aligned}
DR[dB]=20×log((2NFSR)/23FSR/22)=log21020×N+20×log(26)≈6.02N+1.76
这里引出几个问题:
最大均方根幅值为什么是
F
S
R
/
2
2
FSR/2\sqrt2
FSR/22 呢?
当输入信号的峰峰值为FSR时,输入信号的均方根最大,所以为上式
最小均方根幅值为什么是
(
F
S
R
2
N
)
/
2
3
(\frac{FSR}{2^N})/ 2\sqrt3
(2NFSR)/23 呢?
这个就要涉及到ADC的另一个参数 量化误差(Quantization error)
量化误差是什么
假如有一个8bit ADC,可分辨出256种电平,输入范围是2.56V,1LSB即为10mV。当输入信号为1.005V时,受分辨率限制,ADC的测量值和实际值之间一定存在误差,这个误差就是量化误差。用专业一点的化来说:“量化误差是在模拟到数字的过程中引入的误差”
ADC的量化误差为
1
2
L
S
B
\frac{1}{2}LSB
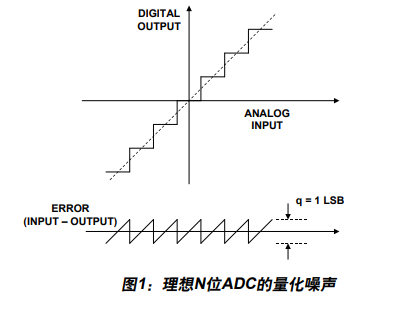
21LSB ,如下图。还是用上面的 例子来说明,
0 ~ 5mV会数字化成0x00,表示0mV;
5 ~ 15mV会数字化成0x01,表示10mV;
15 ~ 25mV会数字化成0x02,表示20mV,以此类推,最大量化误差都为5mV。

可能有人会有疑问:为什么不是
“0 ~ 10mV会数字化成0x00,表示0mV;
10 ~ 20mV会数字化成0x01,表示10mV”
这样进行数字化呢?为什么要有
1
2
L
S
B
\frac{1}{2}LSB
21LSB 的偏差呢?
因为如果没有
1
2
L
S
B
\frac{1}{2}LSB
21LSB 偏差,最大量化误差都为10mV(你可以自己去算一下)。
引入偏差是为了减小量化误差。
量化误差的均方根
仅仅介绍量化误差还不够,这里再解释一个概念:量化误差的均方根

如上图,
有一条连续的 穿过所有无误差的测量点的 直线 (上图虚线)作为实际输入
和一条 表示实际的数字化的情况 阶梯状折线 作为数字化输出,
这两条线之间差可以等效成一个三角波,如上图下面的波形。
这个量化误差的均方根就是这个三角波的均方根
L
S
B
/
12
LSB / \sqrt{12}
LSB/12 ,也就是
(
F
S
R
2
N
)
/
2
3
(\frac{FSR}{2^N})/ 2\sqrt3
(2NFSR)/23
这样就可以解释 :最小均方根幅值为什么是
(
F
S
R
2
N
)
/
2
3
(\frac{FSR}{2^N})/ 2\sqrt3
(2NFSR)/23
那为什么要这样定义量化误差的均方根呢?
人们对于信号采集中的量化误差当作一种噪声进行数学分析,计算得到的实际频谱相当复杂且有时与输入信号有关。为了方便计算,人们使用了一种简化模型,也就是上面提到的方法。这种方法对大多数应用足够准确。(详细解释见文献三)
DR与SINAD
通过前面对于 D R DR DR 的分析可以得出: D R DR DR 可以衡量 在输入交流信号的情况下,ADC的最大测量精度。从另一个角度来看,这是一种特殊的“信纳比”,它的“信”是最大可以接收的信号;它的“纳”是理论上一定存在,无法消除的误差。
实际上,
D
R
DR
DR 与
S
I
N
A
D
SINAD
SINAD 确实有着千丝万缕的联系。
S
I
N
A
D
=
6.02
N
"
+
1.76
SINAD={6.02 N^"}+1.76
SINAD=6.02N"+1.76
上面的式子中将
S
I
N
A
D
SINAD
SINAD 作为实际误差与输入信号的比来代替
D
R
DR
DR 公式中的量化误差 与 最大输入范围,或者说,是用
D
R
DR
DR 的表达形式来表达
S
I
N
A
D
SINAD
SINAD 。
在实际使用中,ADC前面几位(数值大的几位)比较稳定,而后面几位(数值较小的位)会因为噪声而导致数值一直跳变,不能真实反映输入信号的电压值。
这也就是上式中我用 N " N^" N" 而不是 N N N 。这里的 N " N^" N" 就是前面还稳定的,可以准确表示电压值的几位,也就是我们常说的 E N O B ENOB ENOB (有效位数)。
将上面的式子变换一下形式,我们就可以得到开头的公式。至此,有效位数的推导就完成了
下图是TI的一本技术手册里的推导过程,更加简洁,但对于初学者也更加难以理解

DC参数专有名词的解释
在DC信号下有另一套参数
NoiseFreeResolution(无噪声分辨率)
N
o
i
s
e
F
r
e
e
R
e
s
o
l
u
t
i
o
n
=
l
o
g
2
(
2
N
P
e
a
k
t
o
P
e
a
k
N
o
i
s
e
i
n
L
S
B
)
NoiseFreeResolution=log_2({\frac{2^N}{PeaktoPeakNoiseinLSB}})
NoiseFreeResolution=log2(PeaktoPeakNoiseinLSB2N)
PeaktoPeakNoiseinLSB (噪声峰峰值分辨率,我没有找到官方翻译,我不知道这样翻译准不准确)
P e a k t o P e a k N o i s e i n L S B = [ P e a k t o P e a k N o i s e / L S B ] PeaktoPeakNoiseinLSB = [PeaktoPeakNoise/LSB] PeaktoPeakNoiseinLSB=[PeaktoPeakNoise/LSB] 也就是噪声峰峰值除分辨率再向上取整
EffectiveResolution(有效分辨率)
E
f
f
e
c
t
i
v
e
R
e
s
o
l
u
t
i
o
n
=
l
o
g
2
(
2
N
r
m
s
N
o
i
s
e
i
n
L
S
B
)
EffectiveResolution=log_2({\frac{2^N}{rmsNoiseinLSB}})
EffectiveResolution=log2(rmsNoiseinLSB2N)
rmsNoiseinLSB(噪声有效值分辨率)
P e a k t o P e a k N o i s e i n L S B ≈ 6.6 × r m s N o i s e i n L S B PeaktoPeakNoiseinLSB \approx 6.6 \times rmsNoiseinLSB PeaktoPeakNoiseinLSB≈6.6×rmsNoiseinLSB
至于为什么要乘6.6呢?这个和噪声的的分布概率有关。噪声虽然没有确切的波形,但在纵轴上成正态分布,通过概率论的知识计算可以得到这个6.6 (这个推导在很多地方都能查到,比如ADI官网,还有书上也有记载,像是《你好放大器》)
通过上面的两个式子我们可以得到
E
f
f
e
c
t
i
v
e
R
e
s
o
l
u
t
i
o
n
≈
N
o
i
s
e
F
r
e
e
R
e
s
o
l
u
t
i
o
n
+
2.7
EffectiveResolution \approx NoiseFreeResolution+2.7
EffectiveResolution≈NoiseFreeResolution+2.7
过采样
等待施工
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






















所有评论(0)