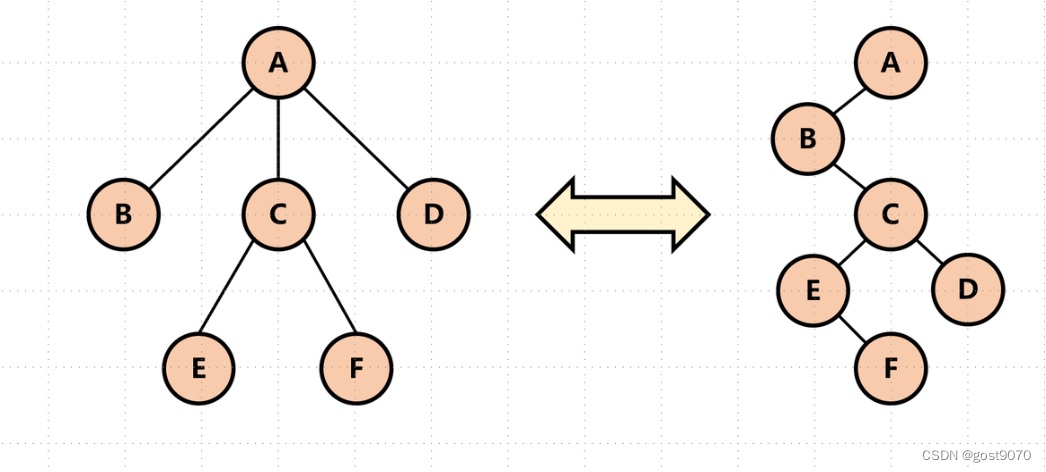
二叉树和树,森林的相互转换
什么是树?
树(Tree)是一种非线性的数据结构。
树是n(n≥0)个节点的有限集。n=0时,称为空树。
树由唯一的根和若干棵互不相交的子树组成。

一棵树
每一棵子树又是一棵树,也是由唯一的根节点和若干棵不相交的子树组成的。

子树

树的定义是递归的
我们可以发现,树的定义是递归。大可以无限套娃!
什么是森林?
很容易想到,由树组成森林。
专业一点的定义是:若干棵互不相交的树的集合。

什么是二叉树?

理解了树,稍加限制条件就是二叉树了。
二叉树就是有限制条件的树。
限制条件有二:

什么是度就不用我讲了吧。我还是讲吧,一句话带过。
节点的度:节点拥有的子树个数或者分支的个数。
在此,我们不妨看看二叉树的节点。

二叉树的节点
下面我们要用的是左孩子右兄弟的方法,
简单三步就能将树和二叉树相互转换。
树 -> 二叉树

一颗普通的树
1.加线。在所有的兄弟结点之间加一条线。
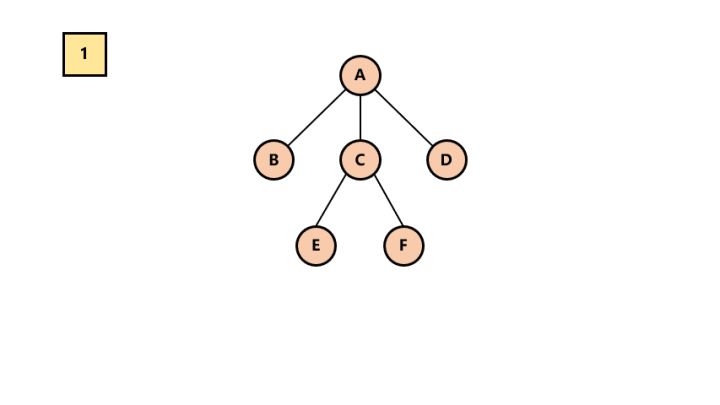
加线
2.去线。树中的每个结点,只保留它与第一个孩子结点的连线,删除其他孩子结点之间的连线。
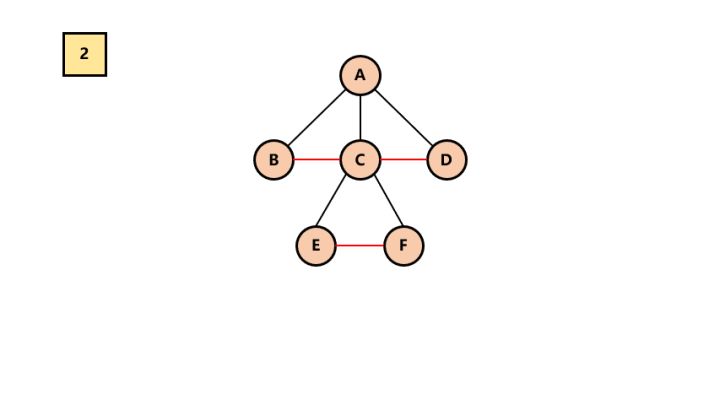
去线
3.调整。以树的根结点为轴心,将整个树调节一下(第一个孩子是结点的左孩子,兄弟转过来的孩子是结点的右孩子)
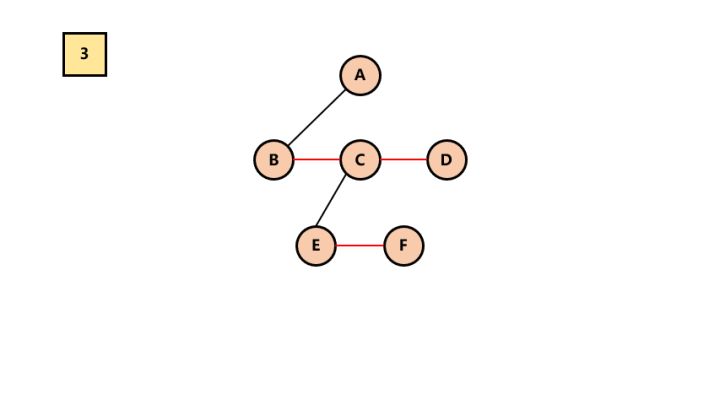
调整
所以最终结果为:

树转二叉树
二叉树 -> 树
知道了树转换为二叉树,那么二叉树转换为树就是个逆过程呗。
1.调整。将二叉树从左上到右下分为若干层。然后调整成水平方向。
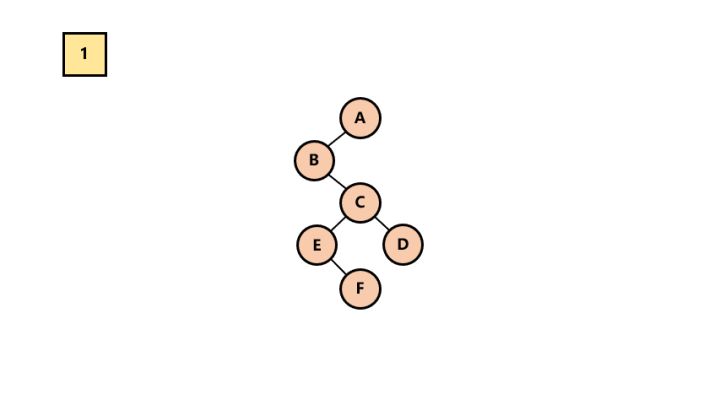
调整
2.加线。找到每一层节点在其上一层的父节点,加线。
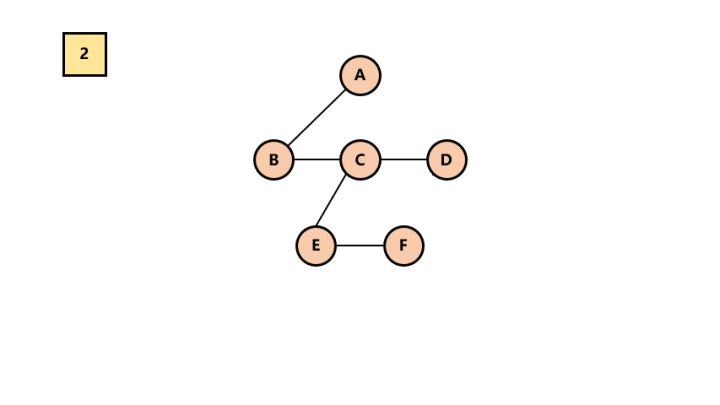
加线
3.去线。去除兄弟节点之间的连线。
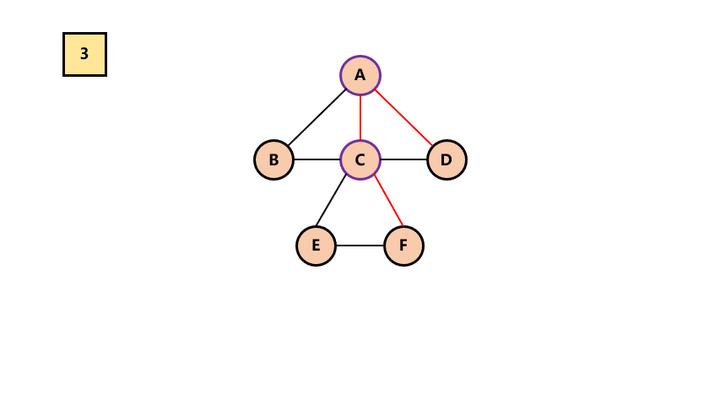
所以最终结果为:

二叉树转为树
二叉树 -> 森林
在此我需要再次强调的是,根据孩子兄弟表示法,根节点是没有兄弟的。
前提:假如一棵二叉树的根节点有右孩子,则这棵二叉树能够转换为森林,否则转换为一棵树。

1.删除右孩子连线。
从根节点开始,若右孩子存在,则把与右孩子结点的连线删除。再查看分离后的二叉树,若其根节点的右孩子存在,则连续删除。直到所有这些根结点与右孩子的连线都删除为止。
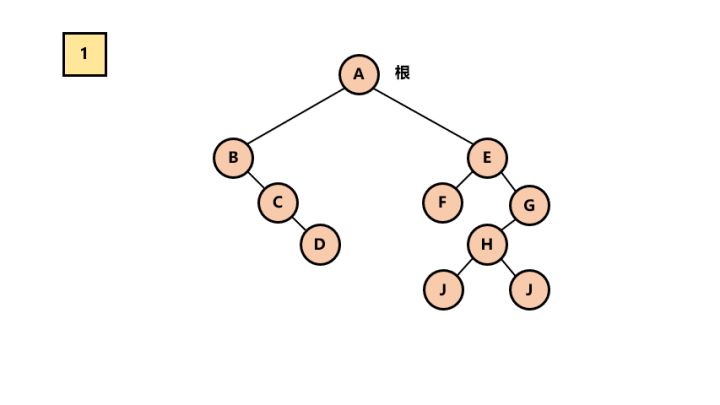
2.将每棵分离后的二叉树转换为树。
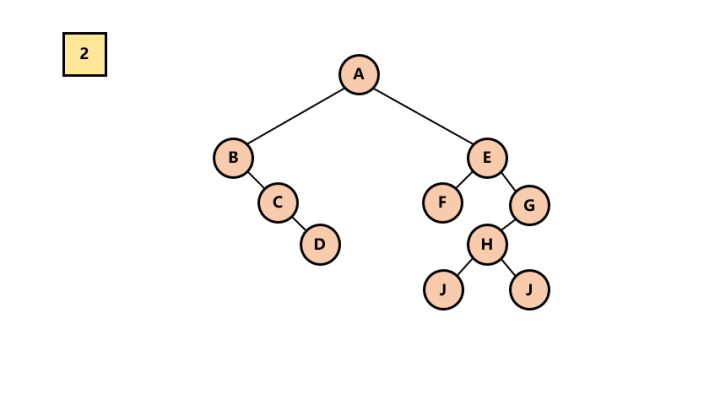
二叉树转换为树
所以最终结果为:

二叉树->森林
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容










所有评论(0)