在用ANSYS进行压力容器应力分析计算的时候，总会出现一些应力集中的问题，而且，有些应力集中点竟然没办法采用倒圆角的办法消除，采用网格加密方法时，甚至应力值比之前更大。这个情况，大家通常称为应力奇异。

以下内容摘自网络：

应力奇异不是会不会引起的问题，而是一定存在的问题。应力奇异是由于应力/应变解是位移解的一阶微分，而在单元节点处形状方程不连续而导致的。通过最最基本的高等数学知识我们可以知道当方程在节点不连续的时候，其一阶微分必定存在奇异，不存在解析解。这个时候可以通过两个甚至多个形状方程的趋势求出在不同单元内的应变/应力微分解。显然当这些形状方程不连续的时候，不同单元内的应力/应变解均不相同，这就是所谓应力奇异的来源。

所以应力奇异没办法采用倒圆角的办法消除，而且网格越密越不容易收敛，并且应力奇异是无法避免的。

根据以上内容，应力奇异出现的位置通常为形状不连续处。而在连续体出现应力奇异的话，那应该重新检查边界条件，确定载荷和位移施加的是否正确。

接下来举例说明：

料仓：筒体直径5500mm，壁厚8mm，锥壳厚度10mm，总高度24705mm，设计压力5KPa，模型对整体设备进行简化，采用1/2模型进行分析，简化后保留足够长的筒体、锥壳，裙座以及筋板和环板，采用SolidWorks曲面功能绘制模型图并导入WORKBENCH如下：

图1 模型

网格划分采用两种不同的尺寸对同一模型进行计算，单元类型均为SHELL 181，CASE 1  总单元数26076，节点数26119；CASE 2 总单元数70205，节点数69303，网格划分如下：

图2 CASE 1 网格

图3 CASE 2 网格

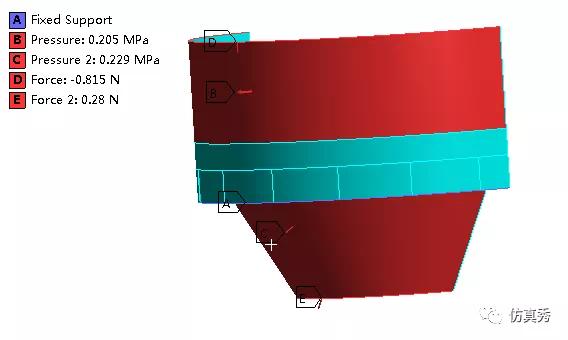
边界条件的施加考虑了模型的简化，筒体端部的等效应力，介质的重量，边界条件如下：

图4 边界条件

结果的后处理，计算整个设备的应力强度Stress Intensity，计算结果如下：

图5 CASE 1 计算结果

图6 CASE 2计算结果

根据以上两种不同的网格划分得知，应力奇异点根据网格的疏密不同计算出的应力值也不相同，网格越密，应力值越大，而且可以明显的看出，最大应力点位置位于筋板的尖角处，而与筋板连接的加强环板上并没有明显的应力奇异，这也印证了上面的论述：“两个甚至多个形状方程的趋势求出在不同单元内的应变/应力微分解。显然当这些形状方程不连续的时候，不同单元内的应力/应变解均不相同”

对于应力奇异，我们通常这样处理：取相邻单元的公共节点的平均值作为局部应力平均解，也就是Average Across Bodies，这样可以在一定程度上缓解应力奇异的问题。计算结果如下：

图7 CASE 1计算结果（Average Across Bodies）

 点击完整阅读全文

应力奇异，你是一个神奇的应力！