一、问题引入

1.什么是动态规划?

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题
核心思想: 通过将问题拆分成一个一个小问题，记录过往结果，减少重复运算
小例子：

A ： "1+1+1+1+1+1+1+1 =？"
A ： "上面等式的值是多少"
B ： 计算 "8"
A : 在上面等式的左边写上 "1+" 呢？
A : "此时等式的值为多少"
B : 很快得出答案 "9"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"

2.什么是背包问题？

背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题，即在总重量不超过W的前提下，总价值是否能达到V？它是在1978年由Merkle和Hellman提出的。
常见分类：

1. 01背包
2. 完全背包
3. 多重背包
4. 分组背包

3.什么是01背包？

01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品，每种物品有且只有一个，并且有权值和体积两个属性。在01背包问题中，因为每种物品只有一个，对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中，则不需要处理。如果选择将其放入背包中，由于不清楚之前放入的物品占据了多大的空间，需要枚举将这个物品放入背包后可能占据背包空间的所有情况。

4.背包问题怎么做？

大致可以分为这几步：

1. 状态表示 / 确定状态变量（函数）
2. 状态计算 / 集合划分 / 确定状态转移方程（递推方程）
3. 确定边界条件

二、例题讲解

1.题目：

2.分析

2.1 第一步：状态表示

最大价值是物品数量i和背包容量j的函数。
设函数f[i][j]表示前i件物品放入容量为j的背包的最大价值。
最终的最大价值就是物品数量i从0增长到n，背包容量j从0增长到m时的f[n][m]值。

2.2 第二步:确定状态转移方程

状态变量：f[i][j]表示前i件物品放入容量为j的背包的最大价值

当前容量为j，我们要考虑第i件物品能否放入？是否放入？

1. 如果当前背包容量j<v[i],不能放入，则f[i][j]=f[i-1][j]
2. 如果当前背包容量j>=v[i]，能放入但是要比较代价
   2.1 如果第i件物品不放入背包，则f[i][j]=f[i-1][j]
   2.2 如果第i件物品放入背包，则f[i][j]=f[i-1][j-v[i]]+w[i]

如果第i件物品放入背包，则背包容量还剩j-v[i],所以要取前i-1件物品放入背包剩余容量j-v[i]所获得的最大价值f[i-1][j-v[i]]。

状态转移方程：

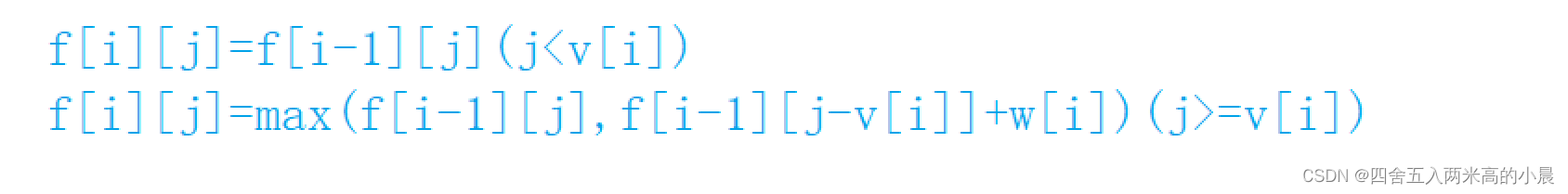
可以画图表示为:

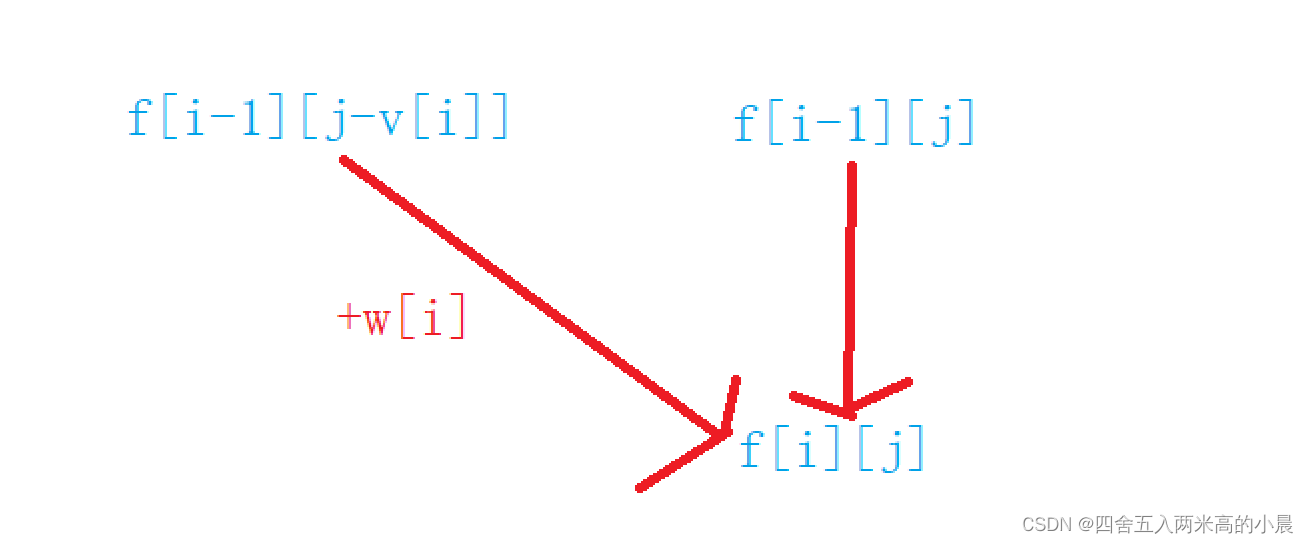
2.3 边界条件

对于01背包来说边界就是f[i][j]=0,即当i=0或者j=0时f[i][j]的值为0。

i=0时，表示背包没有放入一个物品，那么此时背包的最大价值无从谈起，所以为0；
j=0时，表示背包的容量为0，那么此时无法放入物品，所以最大价值也为0；

3.过程表示

3.1 核心代码

3.2 手动计算

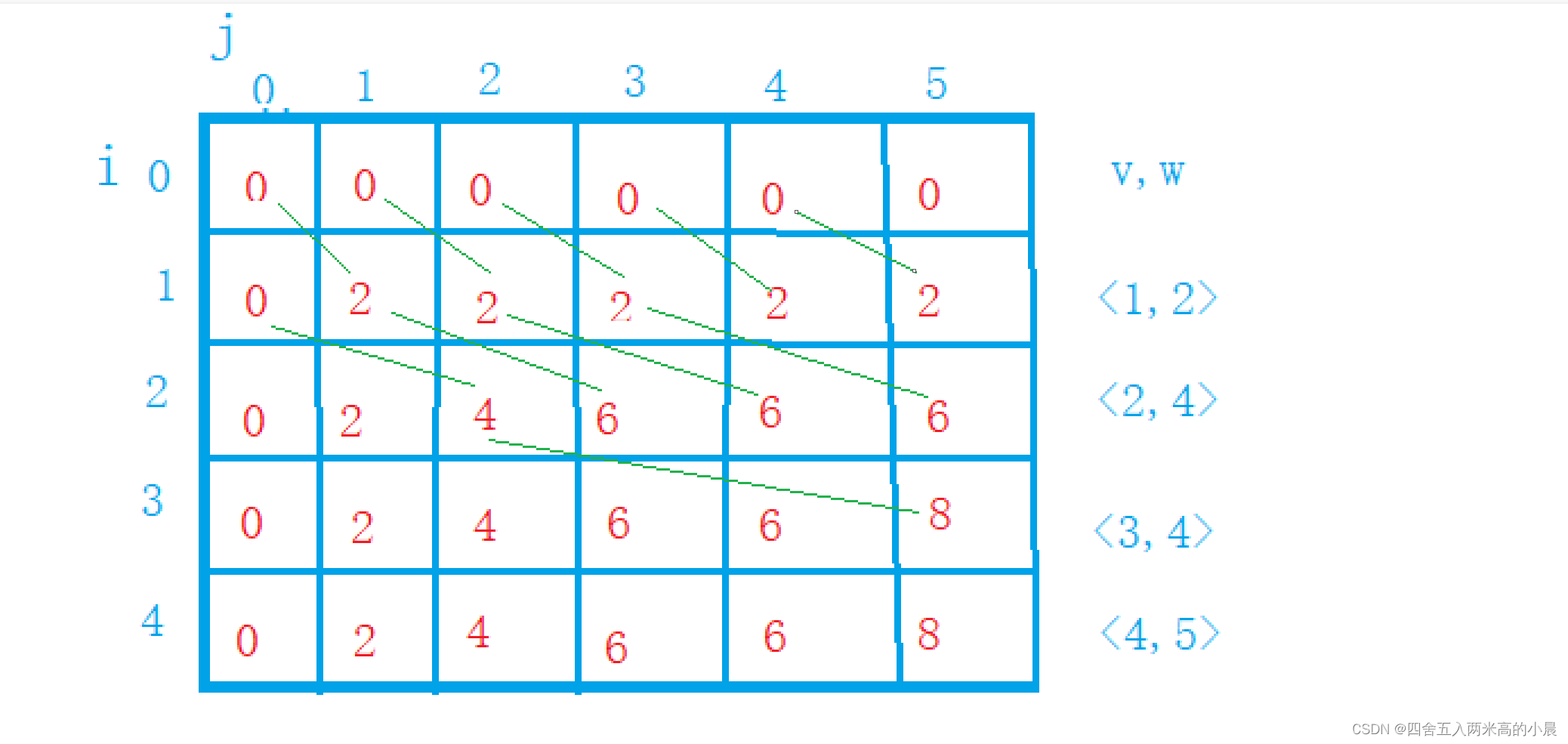
绿色的线表示每次放入第i个物品的情况，并且表示了它的来源

3.3 代码验证

3.4 完整代码

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];//v数组存储体积，w数组存储价值
int f[N][N];
int main ()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
            {
                f[i][j]=f[i-1][j];//将不能放入第i件物品的情况和能放入但是没放入的情况合并
                if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
            }
    cout<<f[n][m]<<endl;
    return 0;
}

三、优化

1.优化目的：

将二维表示优化成一维，减少空间的使用，用一维数组f[j]只记录一行数据，让j值顺序循环，顺序更新f[j]

2.优化后的代码<不一定对哦>

3.程序验证

答案很显然是错误的，为什么呢？？？

4.错误点分析

如果j是顺序更新，那么f[j-v[i]]会先于f[j]更新，当进行比较时，其实是在用更新后的值进行比较，这就导致答案错误，所以解决办法就是j逆序循环。当j是逆序循环时，f[j]会先于f[j-v[i]]更新，也就是说用旧值f[j-v[i]]去更新f[j],相当于用上一行的f[j-v[i]]去更f[j],所以答案正确。

5.改进后的代码

此时还有一个小错误，那就是j的范围不是>=1,因为j若是小于v[i]则会导致f[j-v[i]]里的下标成为负数，所以再进行改进，最终的代码为：